基于SoilGrids的栅格新安江模型参数空间分布估算

童冰星，李致家，姚 成

(河海大学水文水资源学院，江苏 南京 210098)

水文模型参数是对流域下垫面特征的量化，其空间分布估算需考虑下垫面特征空间异质性，是分布式水文模型研究和发展的关键环节和难点问题[1- 2]。中国集水面积200～3 000 km2的中小流域约9 000个[3]，广泛分布在下垫面地理特征观测薄弱的偏远山区，不利于参数空间分布的合理估算，制约分布式水文模型在中小流域的构建与应用。因此，基于高分辨率地球物理数据，开发分布式水文模型参数空间分布估算方法，对于中小流域降雨径流过程精细化模拟，开展洪水风险预警与影响预报、防旱减灾和水土保持等工作具有重要意义[4]。

国内外已有研究学者提出一些分布式水文模型参数空间分布估算方法[5- 7]。Todini等研发的TOPKAPI模型[8]根据世界土壤数据库(Harmonized World Soil Database,HWSD)划分土壤类型，估算土壤饱和渗透系数等参数；Arnold等开发的SWAT模型[9]采用土地利用、植被覆盖数据对土壤湿容重等参数进行估计；Yao等[10]提出的栅格新安江模型(Grid- Xin′anjiang Model，GXM)基于土壤分类推求张力水和自由水蓄水容量。位于秦岭北麓的陈河流域属于中小流域，土壤类型空间异质性较小，然而砂粒、粉粒含量等土壤质地差异可能导致土壤物性参数不同，影响蓄水容量等参数的空间分布[11- 12]。国际土壤信息中心(ISRIC)研发的新版数字土壤制图系统(SoilGrids250mTM，V2.0，以下简称SoilGrids)在2020年5月开始运行[13]。SoilGrids基于WoSIS数据库23万个土壤剖面观测数据和一系列环境协变量拟合土壤脊线预测模型，采用机器学习方法绘制全球范围内250 m空间分辨率、6个标准深度间隔(5 cm、15 cm、30 cm、60 cm、100 cm和200 cm)的土壤特性图(重度、黏粒含量和砂粒含量等)。相较原始版本，新版SoilGrids更新补充土壤剖面观测数据，是目前全球范围内较为完善的数字土壤制图系统。因此，结合新版SoilGrids提供的高分辨率数据，量化土壤质地等下垫面特征的空间异质性，合理估算GXM等分布式水文模型的参数空间分布，是中小流域降雨径流过程精细化模拟研究的重要突破方向。

本文基于新版SoilGrids构建GXM模型参数空间分布估算方案，对陕西省陈河流域16场洪水过程进行模拟，得到降雨径流过程自由水含量动态空间分布，与实测径流过程和新安江模型[14]的计算结果进行对比，量化GXM模型关键参数自由水蓄水容量空间分布特征，开展基于洪水过程划分的参数敏感性分析。

1 计算方法

1.1 土壤物理性质参数空间分布估算

土壤含水量随深度增加变化幅度逐渐减小，自上而下大致可分为活跃层和相对稳定层，通常水分活跃层有机质含量较高[15- 16]。本文基于SoilGrids提供的垂向剖面有机质含量变化趋势，分层概化土壤，估算活跃层厚度空间分布。

(1)

式中：Lh为土壤水分活跃层厚度，mm；Lmin为水分活跃层最小可能厚度，mm；Lmax为水分活跃层最大可能厚度，mm；La为土壤包气带厚度，mm；LM为流域土壤包气带最大厚度，mm，由SoilGrids提供。Lmin和Lmax分别可设置为有机质含量占总量比例为α和β处的土壤深度(图1)，α和β取值参考流域下垫面实地调查和洪水模拟经验。

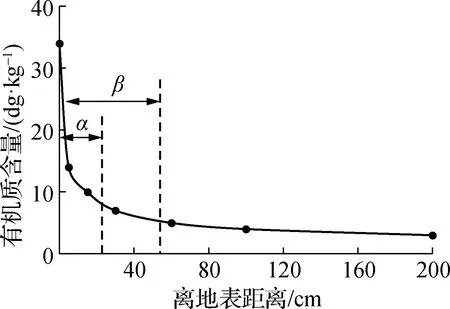
图1 土壤垂向剖面有机质变化示意Fig.1 Change of the organic matter on the soil vertical profile

土壤物理性质参数主要包括凋萎含水量(W)、田间持水量(F)、饱和含水量(B)和饱和渗透系数(K)等，参数估算依据文献[17]。

1.2 GXM模型参数估算

在数字高程模型(DEM)基础上，GXM模型采用D8法[18]识别栅格单元流向，确定栅格汇流演算次序，提取水系网络，区分河道和坡地栅格单元。模型基于蓄满产流理论计算栅格单元产流量，采用自由水蓄水库结构划分地表水、壤中流与地下水3种径流成分，根据栅格间汇流演算次序，将径流演算至流域出口。GXM模型主要参数如表1所示。

表1 GXM模型主要参数

SM、WM(=WUM+WLM+WDM)参数与土壤厚度和土壤物理性质参数相关：

SM=Lh(B-F)WM=La(F-W)

(2)

KI、KG参数反映土壤排水能力：

(3)

CI、CG参数量化径流消退快慢，主要与坡段长度和坡度相关：

(4)

式中：S为地形坡度；Ku和Km分别为水分活跃层和包气带的饱和渗透系数，m/h；H为坡段长度，m；Ti和Td分别为壤中和地下径流进入坡面沟道延迟时间，h，采用式(5)计算。

(5)

2 实例分析

2.1 流域简介与参数空间分布

陈河流域位于秦岭北麓，流域面积约1 350 km2，流域内主河道自西南向东北汇入渭河，其余支流呈扇形汇入主河道。该区域大部分为山区，海拔高程630～3 747 m，受大陆性季风气候影响，多年平均降水量700～900 mm。观测站网包括流域出口处的陈河水文站以及流域内麦场、板房子等9个雨量观测站(图2)，该观测站网收集的2003—2012年降雨、径流观测数据用于洪水模拟。

根据SoilGrids可得到土壤包气带厚度分布。陈河流域包气带最大厚度、分层比例α和β取值分别为1 419 mm、25%和60%，估算得到GXM模型参数空间分布如图3。

图2 陈河流域高程与站点分布Fig.2 Observation stations and Digital Elevation Model of the Chenhe watershed

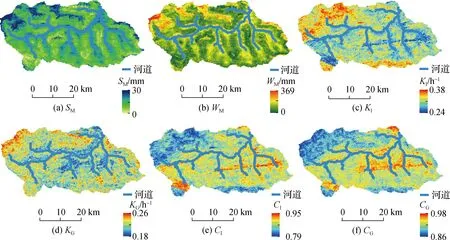
图3 GXM模型水文参数在陈河流域的空间分布Fig.3 Estimated spatial parameters of the GXM model in the Chenhe watershed

2.2 洪水模拟结果

对陈河流域2003—2012年的16场洪水过程进行模拟，统计洪量相对误差(ΔR)、洪峰相对误差(ΔP)、峰现时间误差(ΔT)和确定性系数(CD)等指标，并与新安江模型(XAJ)的模拟结果对比分析(图4)。

GXM模拟的洪量和洪峰相对误差水平为15.3%和14.9%。新安江模型模拟的洪量和洪峰相对误差水平为16.8%和15.4%。新安江模型和GXM模拟结果的确定性系数均值分别为0.79和0.76。相较于新安江模型，虽然GXM模拟结果的确定性系数略小，但洪峰和洪量模拟精度更高，且GXM模拟的陈河流域峰现时间误差水平降低约0.31 h。GXM模拟的部分洪水过程如图5所示。

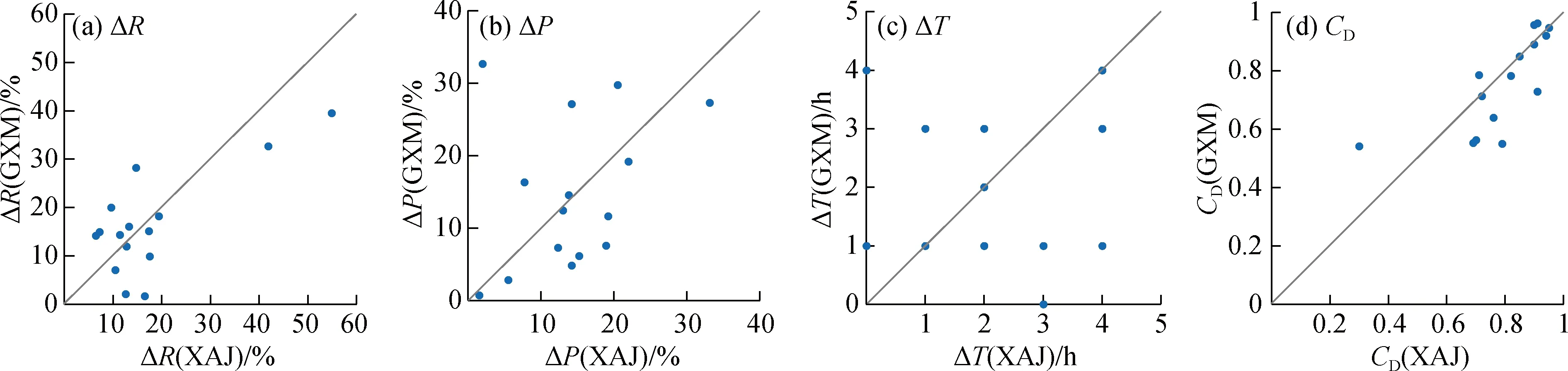
图4 洪水模拟的误差评价指标结果Fig.4 Result of error evaluation indexes for floods simulation

2.3 土壤水空间分布

与新安江模型相比，GXM能够对土壤水饱和度等水文要素的动态空间分布进行较合理地模拟。以陈河流域2003090319号洪水为例(图5(a))，分别在洪水开始后25 h、45 h、65 h、85 h、105 h和125 h输出GXM模拟的土壤水饱和度空间分布结果(图6)。可以看出，初始土壤水饱和度较低(图6(a))，随着降雨持续，土壤水饱和度逐渐增加(图6(b))，在洪峰出现时接近饱和(图6(c))；降雨结束后土壤水饱和度逐渐减少(图6(d)、图6(e))，但仍高于初始时刻的土壤水饱和度(图6(f))。

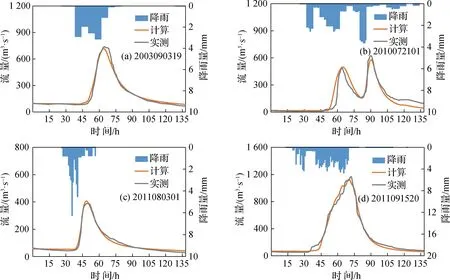
图5 GXM模型洪水模拟结果Fig.5 Floods simulation results using the GXM model

3 参数SM的量化分析

3.1 基于洪水过程划分的SM敏感性分析

研究不同洪水阶段参数SM敏感性，有助于进一步开展参数不确定性分析，为实时洪水预报参数动态调整提供参考，促进降雨径流过程精细化模拟[19]。本文提出五段法，将洪水划分为初始、涨洪、洪峰、落洪和洪尾阶段，研究参数SM在不同阶段对模拟结果的影响。以陈河流域2003090319号洪水为例，将时间t作为自变量计算洪水过程一阶导数(Q′=∂f(t)/∂t)，采用3 h为周期加权移动平均后依次确定：一阶导数值增大位置(A)、最大值(B)、最小值(C)和恢复稳定位置(D)，将洪水划分为初始、涨洪、洪峰、落洪和洪尾阶段(图7)。

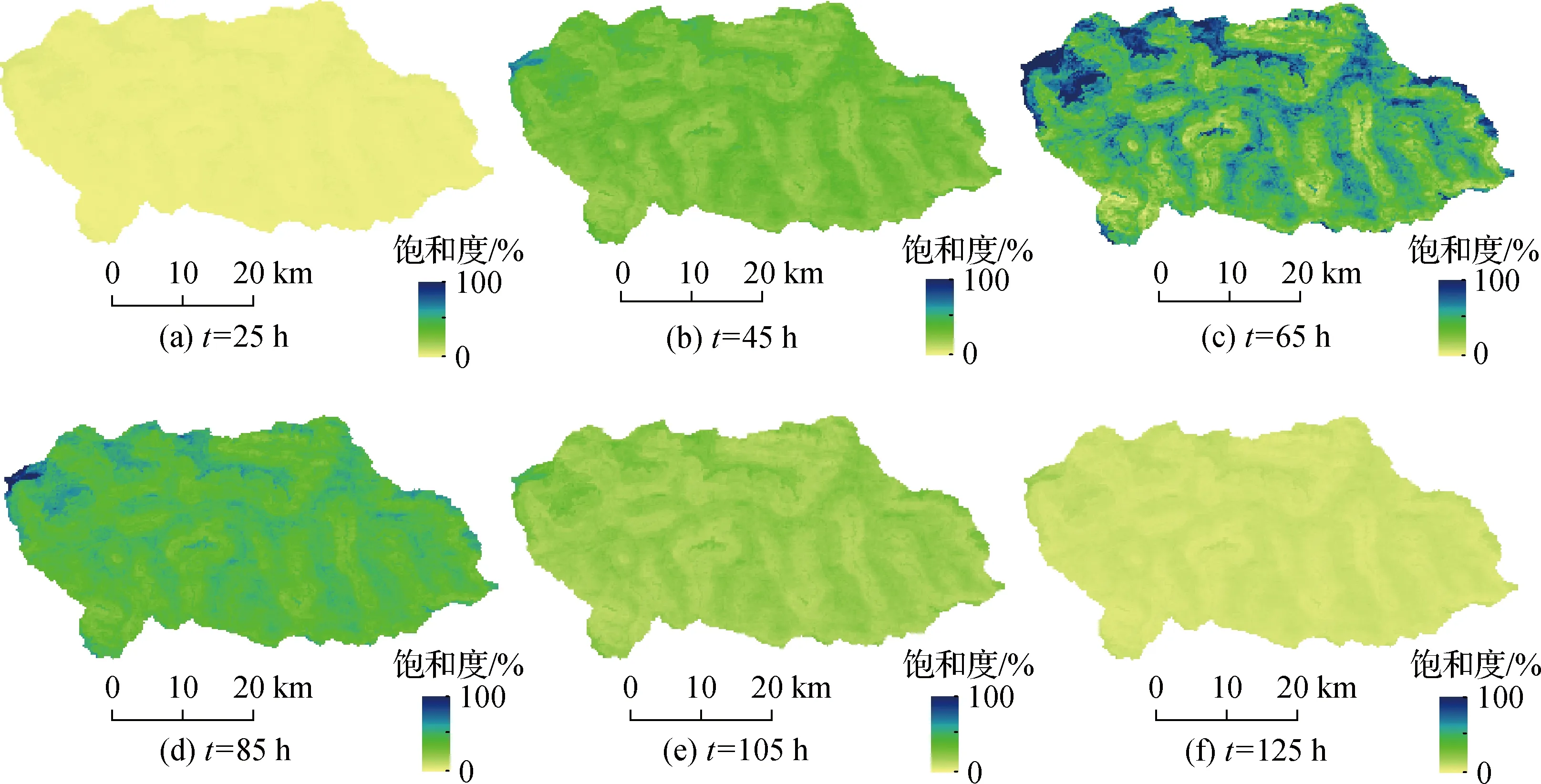
图6 2003090319号洪水过程的土壤水饱和度空间动态变化Fig.6 Spatial dynamics of soil moisture during No.2003090319 flood

图7 洪水阶段划分Fig.7 Phases division of flood

在1～30 mm内，采用0.1 mm为步长设置SM参数值，对2003090319号洪水进行模拟，分别统计涨洪、洪峰、落洪和洪尾段的ΔR和CD，量化参数SM对不同洪水阶段的影响(图8)。

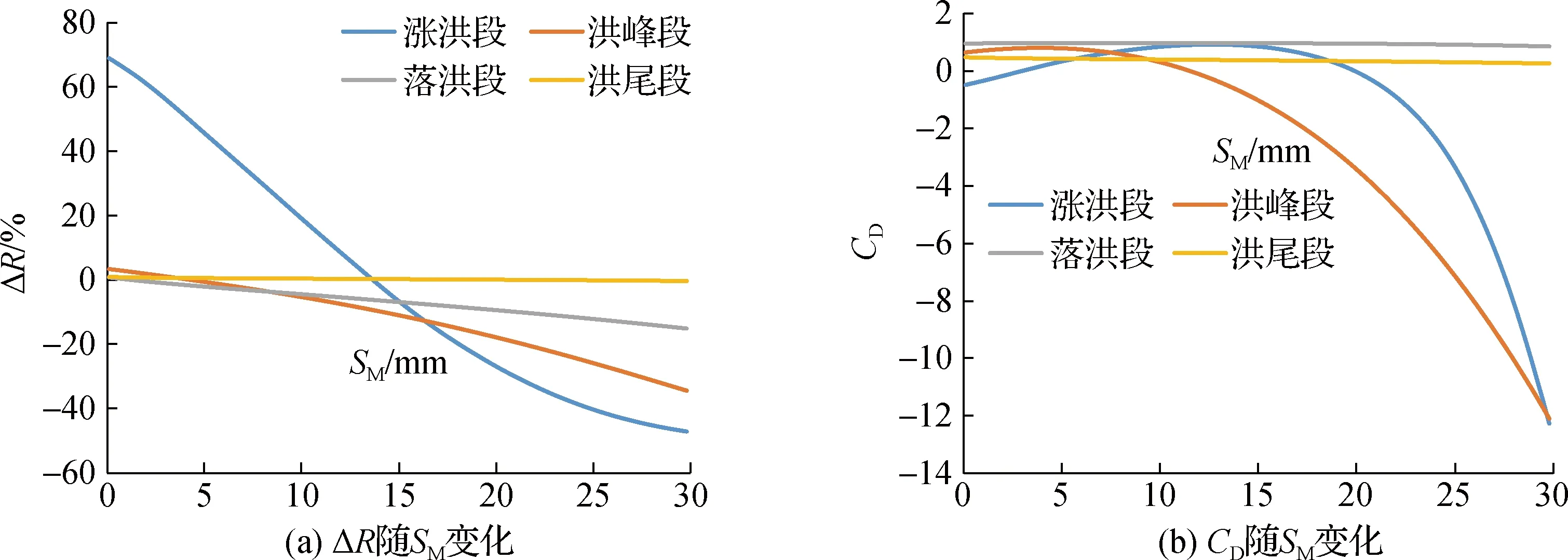
图8 参数SM的敏感性Fig.8 Sensitivity of the parameter SM

对因参数SM变化导致的ΔR和CD在不同洪水阶段的方差进行统计，作为衡量参数敏感性的指标。涨洪段洪量相对误差受SM参数影响较大，敏感性为0.37，明显高于洪峰、落洪和洪尾段(敏感性分别为0.11、0.04和0.003)；SM参数对洪峰段和涨洪段的确定性系数影响较大，敏感性分别为3.76和3.05，对落洪段和洪尾段影响较小,敏感性分别为0.03和0.05。说明SM参数对洪峰和涨洪过程的确定性系数及涨洪段的洪量相对误差影响较大，对退水过程影响小。

3.2 SM空间分布特征的量化分析

大量研究和野外观测实验表明，SM空间分布的合理与否对土壤含水量等水文要素时空分布动态变化模拟有重要影响[20]。为进一步验证参数SM空间分布的合理性，根据陈河流域支流多分布在南侧的地理特点，本文以经纬度为(107°48′ E，33°48′ N)和(108°18′ E，33°52′ N)的2个端点，作1条跨多支流的取样线段(图9)。在取样线段上以250 m为间隔设置样本点，统计样本点处SM值与高程、距离河道远近(G)和土壤有机质含量(M)等下垫面因子的定量关系(图10)。

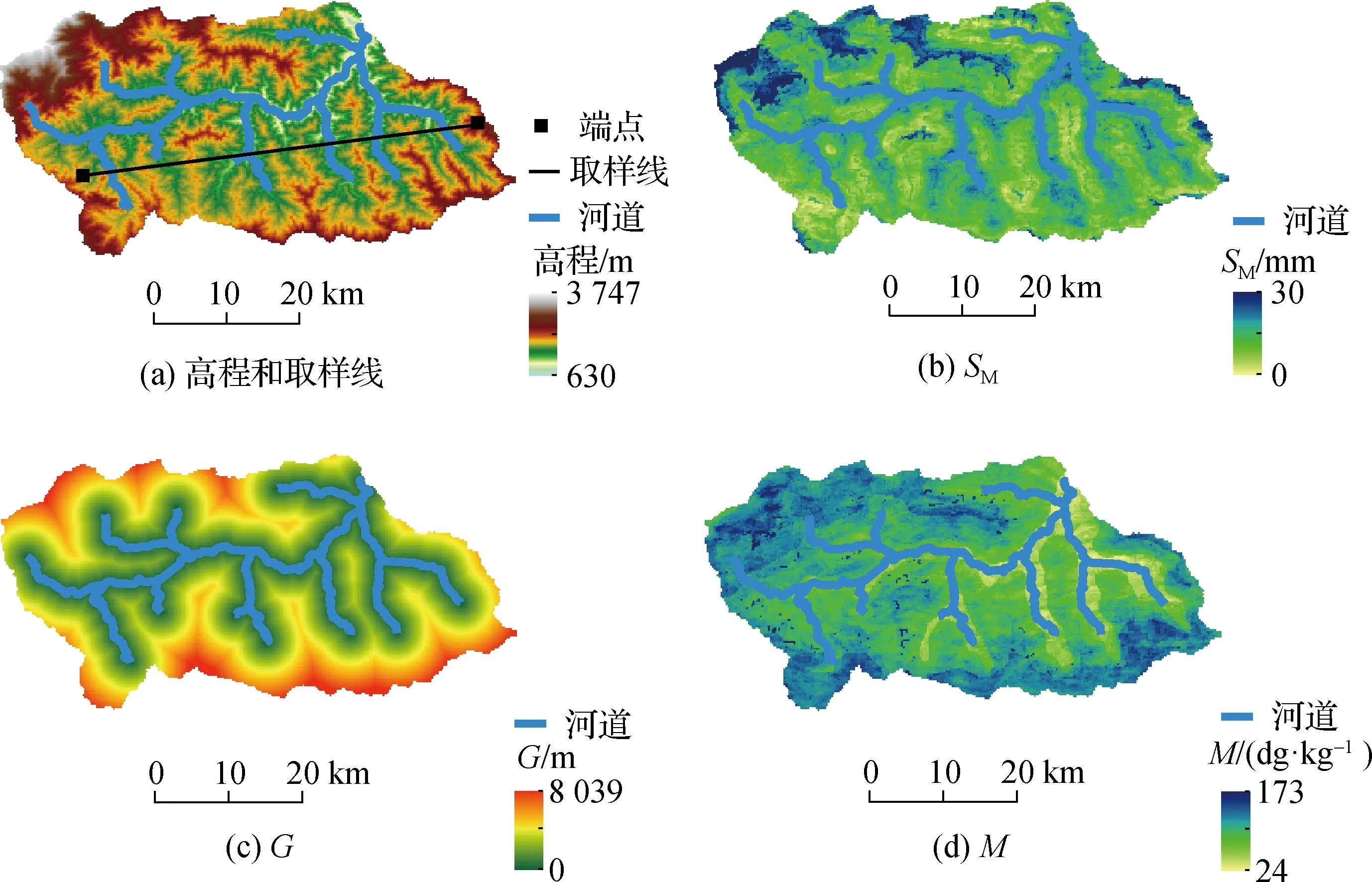
图9 参数SM与下垫面因子(高程、G和M)的空间分布Fig.9 Spatial distribution of the parameter SM and the geographical characters (DEM,G and M)

图10 取样线段上参数SM与下垫面因子(高程、G和M)的相关性Fig.10 Correlation between the parameter SM and the geographical characters (DEM,G and M) in sampling line

由图9和图10可知，SM值随高程、G和M的增加，先减小后增大，相关性分别为0.48、0.44和0.29。水流携带的泥沙在陈河流域谷底沉积，河道附近SM值较大。坡段中部水流流速较快，土壤侵蚀频发，使土壤厚度和SM值减小，而山脊附近有机质含量较高，SM值较大。

4 结 论

本文基于新版全球数字土壤制图系统(SoilGrids)，构建栅格新安江模型的参数估算方案。对陕西省陈河流域2003—2012年16场洪水过程进行模拟，并与新安江模型的模拟结果和实测径流比较，得到以下主要结论：

(1) 结合参数估算方案，栅格新安江模型模拟的峰现时间误差水平降低约0.31 h，洪峰和洪量模拟精度较高，模型能够对土壤水饱和度等水文要素的动态空间分布进行较合理地模拟。

(2) 自由水蓄水容量对洪峰和涨洪过程的确定性系数以及涨洪段的洪量相对误差影响较大，对退水过程影响小。

(3) 自由水蓄水容量在陈河流域河谷和山脊附近较大，坡段中部较小。