基于小波变换模极大值法的涂层信号奇异性检测
杜晶晶 张军芳 刘建晓 殷春英 杜鹏





摘 要:热喷涂涂层厚度多在微米量级,超声检测过程中由于涂层很薄,其上、下界面反射回波将产生叠加与干涉,超声信号波形发生畸变。针对涂层超声信号的奇异性检测问题,该文采用小波变换模极大值法对低碳钢表面上喷涂的铝涂层的超声信号进行奇异性检测,进而测量涂层厚度。实验分析证明,超声测量的铝涂层厚度值与金相测量值基本符合。
关键词:超声检测 涂层 小波变换模极大值 信号奇异性
中图分类号:O47 文献标识码:A 文章编号:1672-3791(2022)03(a)-0000-00
Singularity Detection of Coating Signal Based on Wavelet Transform Mode Maximum Method
DU JingjingZHANG Junfang LIU Jianxiao YIN Chunying DU Peng
(Department of Physics and Electronic Information Hengshui University,Hengshui, Hebei Province,053000 China)
Abstract: The thickness of thermal spraying coating is mainly in the order of micron. In the ultrasonic testing process, because the coating is very thin, the reflection echo of the upper and lower interfaces will produce superposition and interference, and the ultrasonic signal waveform will be distorted. In order to detect the singularity of ultrasonic signal of coating, the wavelet transform mode maximum method is used to detect the singularity of ultrasonic signal of aluminum coating sprayed on the surface of low carbon steel, and then measure the thickness of coating. The results show that the thickness of aluminum coating measured by ultrasonic is consistent with that measured by metallography.
Key Words: Ultrasonic testing; Coating;Modulus maxima of wavelet transform;Signal singularity
目前,热喷涂技术已在医疗器械、核工业、船舶制造业以及航空航天等诸多领域中得到了广泛应用,而热喷涂零件中的涂层厚度测量也开始成为当今工业领域的重点研究内容[1]。通常,热喷涂层的厚度属于微米级别,这对于其厚度的无损检测具有重要价值,其中利用涂层上、下表面回波信号声程差和涂层材料的声速来获取涂层的厚度是最简单直观的一种方法[2]。对于薄涂层而言,在超声波的传输过程中,其上下界面上的回波会有叠加干涉产生,波形畸变,进而无法直接在时域内对其界面回波所达到时的具体位置进行直接識别。在这样的情况下,不仅需要找寻一种有效的表征,同时也需要找到一种方法来进行涂层中奇异性超声信号的处理。
关于涂层中具有奇异性的信号检测,国内外的相关研究比较多。在这些研究中,通常都借助于频谱分析技术中的傅里叶变换对信号中的奇异点进行归一化处理。通过研究可知,传统形式的傅里叶变换并不能敏锐感知到信号中的奇异性,而在小波分析理论中,可对小波变换模具体的极大值曲线进行跟踪,以此来检测奇异点在信号中所处的具体位置。目前,小波变换已经在对信号进行奇异性检测的过程中得以广泛应用[3]。基于对超声无损测厚原理及小波分析方法的研究,该文将采用小波变换模极大值法检测涂层的超声信号奇异点,并计算得到低碳钢表面的铝涂层厚度验证该方法的有效性。
1小波变换
超声信号并不平稳,在对变异信号处理过程中仅可以通过时域以及频域来进行分析。小波变换是近年来一种新兴的分析方法,其应用基础是傅里叶变换。该方法突破了传统傅氏变换中不具备分辨力的时域限制,可分析特定时段、频带中的信号,对频域以及时域的局部化性分析良好。同时,因其频率方面所应用的时域取样步长属于逐渐精细形式,可对信号中的任何一个细节进行聚焦。经小波变换后信号中的奇异性将会在很多尺度上呈现出瞬态或是突变特性,这使得小波变换方法具有很好的应用意义,且发展潜力也十分显著。
检测突发信号的连续可微的小波基在小波变换处理中具有关键作用。其中的墨西哥帽小波是高斯函数的标准二阶导数,在地球物理学上常被称为Ricker小波,在该领域经常被用于地震数据建模[4]。Mexihat小波满足小波允许条件;在时域和频域具有很好的局部化[5];属于连续性低通平滑形式函数的导数,在应力波中奇异性检测方面的优势十分显著;具备对称性及二阶消失矩,在应力波脉冲形应变检测方面十分适用。基于此,该文选取墨西哥帽小波对涂层奇异性信号进行检测。
2奇异性检测
连续小波变换以信号频率具有的自适应能力作为依据,对时间窗进行合理选择,在对由于瞬时变化出现的高频信号信息进行分析时,小波变换可对细节信息实现更好地观察。对f(t) L2(R),其连续小波变换定义为 [5]。
定义 和 的小波变换: , 。
设 ,对一实函数f(t)有如下形式的小波变换:
式中 和 分别与通过 进行光滑处理后的函数一阶和二阶导数成正比,一阶导数的极值点和二阶导数的零点相对应,且为这一函数拐点;同时一阶函数最大绝对值与突变点相对应。基于此, 幅值极大绝对值点与f(t)函数中的突变点相对应, 函数的零点与 函数的拐点具有一致性。
假设 是由f(t)经小波变换得来的函数,在a0这一特定尺度上,对f(t)这一函数做小波变换,便可获得其连续变换系数,记作Wf (a0,b),在某特定领域中,若b0中任意一点b都能和 相符,我们便将(a0,b0)点叫作极大值点,属于小波变换系数所具有的模极大值[6]。
3 试验与验证分析
该次试验中,选取的试样是在钢基板上通过热喷涂技术制备出的涂层,该涂层属于纯铝涂层,其厚度在180~200μm之间,在通过光学显微镜进行观测时,获得到的显微金相形貌如图1所示,其中的序号1和序号2是采样点,序号1的采样值是218μm,序号2的采样值是270μm。该试验通过接触式超声纵波脉冲回波技术来进行铝涂层中的超声信号检测,以此来发现其奇异性,检测中主要参数如下:(1)所选探头为接触式纵波单晶片平探头,其型号是10C6N;(2)所选晶片材料为钴钛酸铅形式的陶瓷,其中心频率f的取值是10MHz,晶片直径d的取值是6mm。
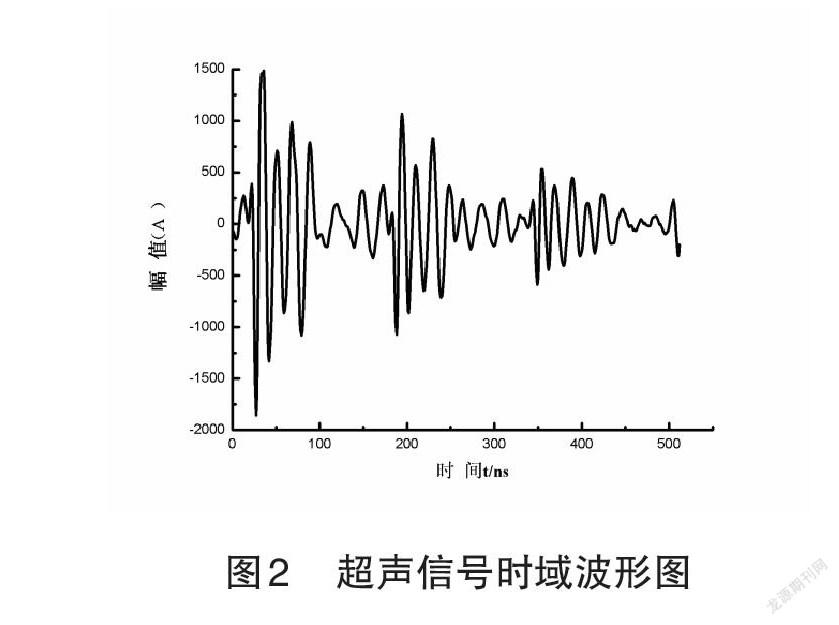
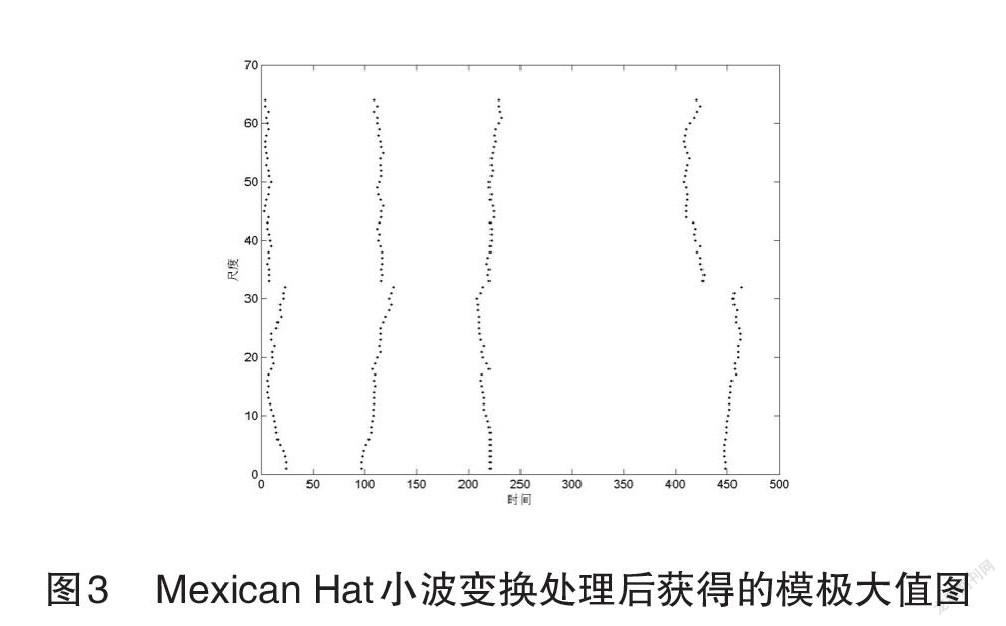
图2是经超声检测在该铝涂层中获取到的信号时域波形(以采样点2为例)。在该薄涂层内,超声波在传播过程中将会在两个界面上出现反射回波叠加现象,其中的一个界面在耦合剂与铝涂层之间,另一个界面在铝涂层和基体之间,图2中用椭圆标记出的位置便是回波叠加产生的位置,在该位置上,波形会出现突变现象,无法在时域内直接对这两个界面上回波产生的具体位置直接进行判断。基于此,该次通过Matlab软件来进行时域内原始信号的连续小波变换,并对其模极大值进行获取,图3就是以采样点2为例,通过Mexican Hat小波进行小波变换处理之后所获得的模极大值图。
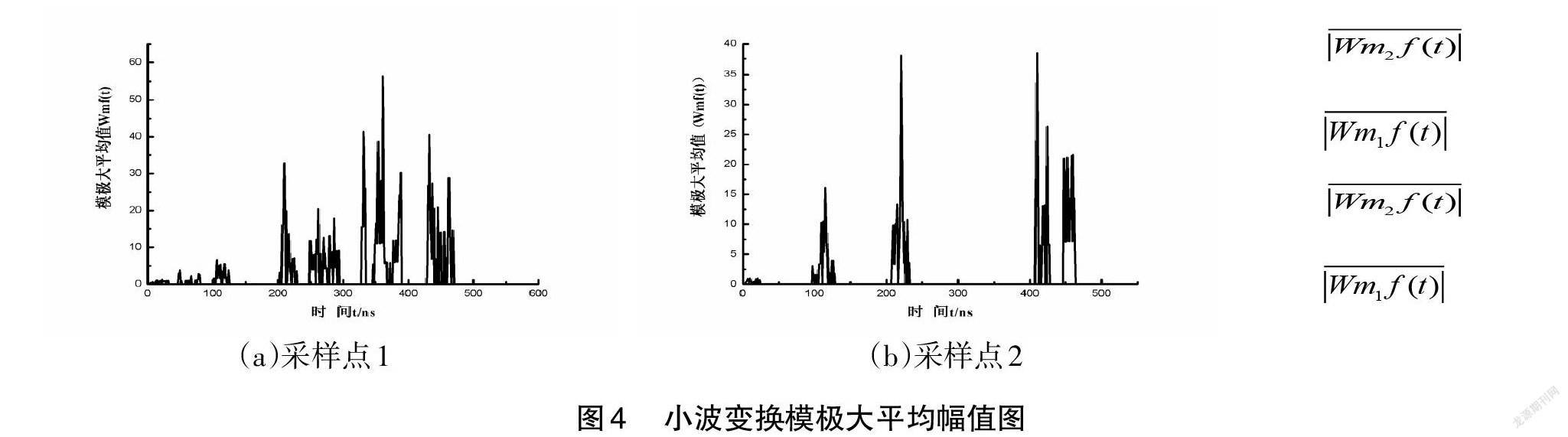
对于与小波系数中的极大值点具有对应关系的信号奇异点,如果在某一刻信号出现了奇异,经小波系数处理之后获得的模极大值图上的模极大值连线就会反映出很大尺度范围的变化。因信号发生奇异的位置处于这个较大的尺度范围中,所以这一范围里的所有小波系数都会获得到相应的模极大值,且这些模极大值也具有最大的处理能量。為实现单一尺度情况下奇异点所处时刻误差的有效降低,该次研究中,特对每一个尺度上每个时间点上的模极大值都进行了平均值获取,这些平均值所具有的幅值将会反映出每一个时间点内的能量值和信号所具有的奇异程度。图4是这一试样中的两个采样点经小波变换之后获得的平均极大值幅值图。
观察图4(a)、(b),两 位置上的小波系数平均极大值已经达到了最高值,具有最大的能量,因此也具有最大的奇异性;在两 位置上,其平均模极大值已经超出了附近的平均模极大值能量,其信号所具有的奇异性也比较大。通过小波变换模极大值方法的信号奇异性检测原理可知, 所对应的是回波达到了耦合剂与铝涂层之间界面的时刻; 所对应的是回波达到铝涂层与低碳钢之间界面的时刻。而回波到达这两个界面的时间点差值就是铝涂层内超声波往返一次所需的时间。依超声测厚公式 ,经查超声波在铝涂层中的传播速率为6375m/s,计算可得两采样点的厚度值分别为226μm、261μm。相比较光学显微镜所测量到的涂层厚度(218μm、270μm)而言,其计算误差符合要求,可用来进行薄涂层厚度的无损检测。表1是铝涂层试样厚度的计算精度。
4 结语
在薄层介质内,超声波的传播会在多层界面位置出现反射回波叠加现象,进而导致波形突变,而通过小波变换模极大值的方法来进行信号奇异点检测则十分有效。该次主要对Mexican Hat以及Sym4这两种小波进行了特性比对,并进行了相应的验证分析,经分析发现,前者在薄涂层中的信号异常检测中更加适用,可对厚度范围在180~200μm之间的纯铝薄涂层厚度进行检测,相比较金相检测而言,该方法具有更小的计算误差。由此可见,该方法在薄涂层厚度无损检测中具有非常好的适用性和可行性。
参考文献
[1] 王胜新.基于超声的多层异质薄膜材料厚度检测方法研究[D].成都:电子科技大学,2017.
[2] 罗文,张伟,赫丽华,等.碳纤维复合材料表面雷达吸波涂层超声测厚方法研究[J].失效分析与预防,2021,16(4):233-237.
[3] 郑茜.基于插值小波的信号奇异性检测和图像边缘提取[D].成都:电子科技大学,2018.
[4] 高晓旸,严如强.小波变换理论及其在制造业中的应用[M].姚福来,译.北京:机械工业出版社,2019:32-33.
[5] 孙延奎.小波变换与图像、图形处理技术[M].2版.北京:清华大学出版社,2018:136-138.
[6] 宋颖,施文杰,孙宝臣.基于自适应连续小波模极大值算法的车轮擦伤定量评估[J].振动与冲击,2021,40(12):168-178,209.

