基于LMD形态滤波的LSSVM方法研究
孟良,许同乐,马金英,蔡道勇






摘要:在轴承的故障诊断中,为了解决核函数在最小二乘支持向量机中参数选择困难及稀疏性差的问题,提出了局部均值分解(LMD)形态滤波的最小二乘支持向量机(LSSVM)方法。该方法首先利用LMD对信号进行分解得到PF分量,并对信号做相关分析去除虚假分量,形态滤波降噪后再进行LMD分解得到新PF分量,提取能量特征;其次,对LSSVM的核函数进行改进,解决核参数选择的问题;应用特征加权法对拉格朗日参数进行特征加权,取其加权平均值作为剪枝方法的阈值,降低稀疏性;最后将能量特征信号输入LSSVM中,对信息进行训练预测。实验表明,应用该方法能快速有效地对轴承故障信号进行自适应的分类及轴承故障的判断。
关键词:局部均值分解; 形态滤波; 剪枝方法; 最小二乘支持向量机; 故障诊断
DOI:10.15938/j.jhust.2022.01.012
中图分类号: TH707 文献标志码: A 文章编号: 1007-2683(2022)01-0092-08
There Search of LSSVM Based on LMD Morphology Filter
MENG Liang1,XU Tongle1,MA Jinying2,CAI Daoyong3
(1.School Mechanical Engineering, Shandong University of Technology, Zibo 255049, China;
2.School of Agriculture Engineering and Food Science, Shandong University of Technology, Zibo 255049, China;
3.Shandong Keda M&E Technology Co.,Ltd., Jining 272000, China)
Abstract:In the diagnosis of bearing, the LSSVM method research with LMD morphological filtering was put out in order to solve the problem about the kernel function parameter selection and the bad sparsity of least squares vector machine (LSSVM). First, the LMD was used to decompose the measured signal and PF components were obtained. The correlation analysis was carried out to remove the false components, and the noise of PF components was reduced by morphological filtering. The LMD decomposed the recombinational signal and obtained new PF components, and energy characteristics were got from the new PF component. Secondly, the kernel function of LSSVM is improved to solve the problem of kernel parameter selection. Lagrange parameters were weighted by feature weighting method, and their weighted average value was taken as the threshold of pruning method to reduce the sparsity. Finally, energy characteristics were put into LSSVM to train and predict. Experiments showed that this new method could fulfil adaptive classification of bearing fault signals and definite fault conclusion quickly and effectively.
Keywords:local mean decomposition; morphological filtering; pruning method; least squares support vector machine; fault diagnosis
0前言
Suykens等[1]于1999年提出了最小二乘支持向量機(least squares support vector machine, LSSVM)方法。将最小二乘线性系统引入到传统支持向量机(support vector machine, SVM)中得到LSSVM方法,传统SVM中的约束条件为不等式约束,LSSVM方法中则转换成等式约束条件,其训练过程就变成了对线性方程组的求解,提高了传统SVM的求解效率,降低了学习难度,性能在很大程度上得到改进[2-3]。但是,LSSVM丧失SVM稀疏性的同时仍存在核参数选择困难问题,成为制约LSSVM应用的障碍[4-5]。
针对LSSVM出现的上述问题,本文提出了基于局部均值分解(local mean decomposition, LMD)形态滤波的LSSVM方法,并应用于轴承的故障诊断中。该方法为了得到PF分量首先应用LMD算法[6]对故障信号进行自适应的分解,使用形态滤波[7]对乘积函数(product function, PF)分量进行降噪,去除虚假分量使用相关分析方法,之后重组信号,对重组后的故障信号再次利用LMD进行分解[8-9],提取能量特征,并进行归一化处理;其次,为了解决LSSVM存在的核参数选择困难以及稀疏性差的问题,采用适应数据特点的核函数与自适应的剪枝阈值的方法;最后,在改进的最小二乘支持向量机中输入归一化处理后的能量特征,对信号特征进行训练、预测,从而对故障信息进行判断。
1LMD形态滤波以及特征提取
LMD方法[10-13]是一种自适应信号分解方法,把故障信号分解得到若干个瞬时幅值的乘积函数PF分量和一个残余分量r(t),即
x(t)=∑ni=1PFi+r(t)(1)
LMD分解可完整地保留原始信号信息,将信号的时频分布体现在所有的PF分量的瞬时幅值与瞬时频率中。形态滤波通过开运算和闭运算实现对故障信号的滤波降噪[14-15]。
本文故障信号降噪采用组合滤波器的方式。LMD形态滤波信号处理及特征提取步骤如下:
步骤1:分析测量物体的结构特征;
步骤2:对测量的信号x(t)进行LMD分解,得到i个单分量调幅调频PF1i分量,通过相关分析,去除虚假分量,得到PF2i分量;
步骤3:对PF2i分量采用组合滤波的方式进行降噪处理,采用正弦型结构元素,得到PF3i分量;
步骤4:对得到的PF3i进行信号重构得到信号x′(t),对x′(t)再次LMD分解,得到分量PF4i;
步骤5:根据步骤1的结构分析,对PF4i进行分类:PF′4i含有主要信息的高频分量,PF″4i含次要信息的低频分量。提取PF′4i的能量特征为E,并对其进行归一化处理,如式(3),并将E′作为输入LSSVM的特征向量。
E=[e1,e2,…,em](2)
E′=E∑mi=1ei=[e′1,e′2,…,e′m](3)
本文采用的故障信号处理过程为:LMD分解—相关分析—形态滤波降噪—信号重组—LMD再分解。因为噪声会对LMD分解的效果产生影响,所以该方法有效提高了故障信号的降噪效果以及特征提取的准确度。为了减少输入LSSVM中的向量维度,步骤5中的信号特征提取方法从源头上进行了改进,保证数据输入时的可信度。
2最小二乘支持向量机
LSSVM在目标函数中,将松弛变量用误差平方和来代替,进而转化成求解线性方程组的问题,能够解析参数[16-17],提高了求解效率。但是在改进SVM时,会降低LSSVM的稀疏性,输入信号维度过于庞大,且存在SVM在参数以及核函数选择上的受限问题。
2.1最小二乘支持向量机
对于LSSVM可采用下式描述未知函数:
yi=ωTφ(xi)+b+ξi(4)
其中:yi为目标值;ω为权矢量;φ(·)为核函数;xi为输入量;ξi为误差变量;b偏差量。核函数能将输入的特征信号映射到高维特征空间中。
LSSVM函数优化问题的描述如下:
minJ(ω,ξi)=12||ω||2+12γ∑li=1ξ2i(5)
其中:J为结构风险最小化函数;γ为可调参数;l为输入量个数。样本错分的惩罚力度用可调参数γ表示,其值大小与错分样本的惩罚力度成正比。当核函数参数一定,γ增大到一定程度时,LSSVM的分类效果则逐渐趋于稳定,实现特征空间的线性可分。
最优解可以通过对偶形式得出,根据对偶形式引入拉格朗日函数,如下式:
L=12||ω||2+12γ∑li=1ξ2i-∑li=1αi(ωTφ(xi)+b+ξi-yi)(6)
式中:αi为拉格朗日乘子。进一步得式(7),如下:
Lω=ω-∑li=1αiφ(xi)=0
Lb=∑li=1αi=0
Lξi=αi-γξi=0
Lα=yi-(ωTφ(xi)+b+ξi)=0(7)
分别消去ω和ξ,得到求解结果,并根据Mercer定理进一步处理,可使用核函数K(x,xi),则LSSVM的回归函数为:
f(x)=∑li=1αiK(x,xi)+b(8)
式(8)中的αi、b可由式(7)求出,核函数为满足Mercer条件的任意半正定函数。
2.2核函数及核参数的选择
核函数的作用是将数据映射到高维空间,增加线性学习器的计算能力,克服维数灾难。本文将4种轴承故障信号特征向量按能量大小进行排序,如图1,以此选择LSSVM的核函数。
由图1可得,4种故障信号的特征向量能量分布无规则,且是非线性的。从能量分布的总体走势上来看,表现为第一区间是反比例函数。根据该特点,提出了一种平移不变的核函数,如式(9)所示:
K(x,y)=ke||x-y||2/z+1(9)
式中:k(k>0)为待分类的数据种类数。z可由式(10)表示:
z=∑||x-y||/n(10)
其中n为该类特征向量个数。
核函數中的参数均由数据种类以及特征向量的能量决定,解决了核函数参数确定困难的问题。式(9)所采用的反比例函数结构的核函数,满足平移不变核函数判定定理,证明如下:
F[K(w)]=(2π)-n/2∫Rne-jω·xK(x)dx=
(2π)-n/2∫Rne-jω·x·ke||x||2/z+1dx≥0(11)
2.3加权LSSVM算法
针对LSSVM稀疏性降低的问题,本文采用剪枝的方法[18-19]。在剪枝方法中,其阈值设置影响剪枝效果[20],为此提出了一种自适应阈值的方法,来代替主观的阈值设定。其方法如下:
1)计算ai的权值Pi=|ai|∑|ai|;
2)求解ai的加权算术平均值η=∑Ni=1Pi|ai|N,并将η作为剪枝方法的阈值。
3基于LMD形态滤波的LSSVM方法
将LMD算法与形态滤波相结合,使故障信号预处理与特征提取一步完成,并将该方法与改进的LSSVM算法结合,提出LMD形态滤波LSSVM方法,该方法结构紧凑、计算简单。
如图2为LMD形态滤波LSSVM的总体流程图。所提方法的包含3个步骤:
步骤1:将原始故障信号进行LMD分解,对分解的PF分量进行形态滤波降噪,降噪后将PF分量进行重组得到重组故障信号;
步骤2:将重组信号作为新LSSVM的输入,根据重组故障信号的特征向量能量分布,提出了一种平移不变的核函数,解决了核函数参数确定困难的问题,通过比较拉格朗日乘子及其加权算术平均值,判断新LSSVM的分类效果;
步骤3:当η≤|ai|时,去掉小于η的|ai|及相关特征向量,其余保留;当η≥|ai|时,将|ai|带入式(9)中,并输出故障分类结果。
4实验研究
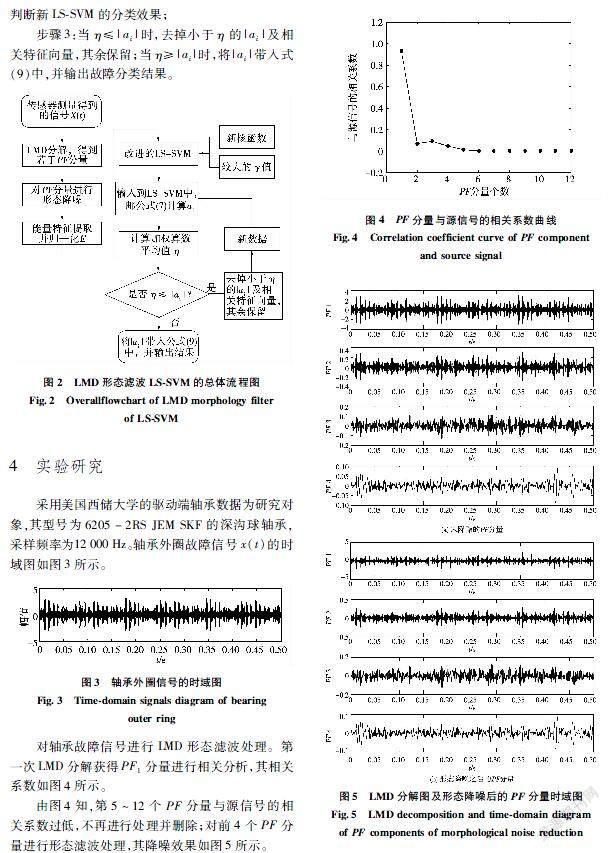
采用美国西储大学的驱动端轴承数据为研究对象,其型号为6205-2RS JEM SKF的深沟球轴承,采样频率为12000Hz。轴承外圈故障信号x(t)的时域图如图3所示。
对轴承故障信号进行LMD形态滤波处理。第一次LMD分解获得PF1分量进行相关分析,其相关系数如图4所示。
由图4知,第5~12个PF分量与源信号的相关系数过低,不再进行处理并删除;对前4个PF分量进行形态滤波处理,其降噪效果如图5所示。
对图5(b)中的信号进行重组得到信号x′(t),其时域图如图6所示。以信噪比(SNR)作为降噪精度的评判标准,得到对x(t)的降噪效果,通过公式(12)可以计算出SNR=5.4352。由此可得该方法能对振动信号进行有效地降噪,且简单实用。对重组信号进行LMD分解得到PF2分量。
SNR=10lg[∑Ni=1x2(t)/(∑Ni=1(x(t)-(t))2)](12)
由于轴承结构的特殊性,LMD分解后的故障信息主要集中在前4个高频分量中,提取前4个高频分量作为提取特征向量的原始数据。根据轴承故障类型,将测量数据分成4类,每类故障包含30组数据,每组数据6000点。其中测试数据从每类中随机抽取10组,共240000个数据点;训练数据从每类中随机抽取5组,共120000个数据点。随机抽取的外圈故障的训练数据如表1所示。
将抽取的训练数据输入到改进的LSSVM中进行分类训练,其分类效果与使用径向基核函数的LSSVM进行对比,如图7所示。2种LSSVM分类方法的参数γ=10、δ=0.4。
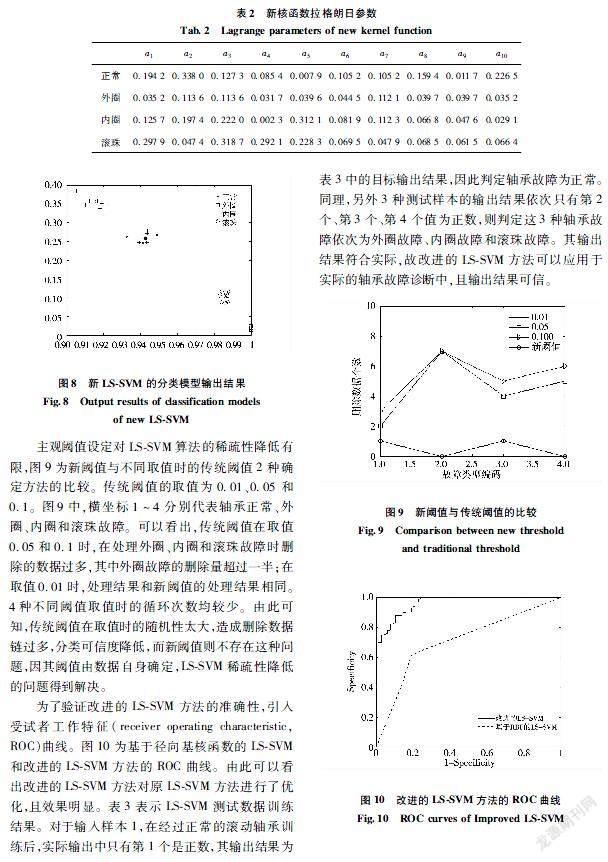
从图7(a)中可以看出,基于径向基核函数的LSSVM成功将正常与外圈故障进行分类,但滚珠故障与内圈故障没有完成分类;图7(b)中表明新的核函数成功将4种类型的故障进行分类,说明新的核函数相较于径向基核函数在进行故障分类时更具有优越性。表2为在使用新核函数进行第一次训练时得到的拉格朗日参数。
从表2和新的阈值计算方法可得到4种故障数据的拉格朗日参数的加权平均值,分别为0.02017、0.00803、0.01907、0.02336。将新得到数据重新带入改进的LSSVM中重新训练,数据经过第二次训练即满足要求。由此表明,新的阈值确定方法在一定程度上满足了自适应的LSSVM算法的稀疏性。图8为第二次训练的结果。
主观阈值设定对LSSVM算法的稀疏性降低有限,图9为新阈值与不同取值时的传统阈值2种确定方法的比较。传统阈值的取值为0.01、0.05和0.1。图9中,横坐标1~4分别代表轴承正常、外圈、内圈和滚珠故障。可以看出,传统阈值在取值0.05和0.1时,在处理外圈、内圈和滚珠故障时删除的数据过多,其中外圈故障的删除量超过一半;在取值0.01时,处理结果和新阈值的处理结果相同。4种不同阈值取值时的循环次数均较少。由此可知,传统阈值在取值时的随机性太大,造成删除数据链过多,分类可信度降低,而新阈值则不存在这种问题,因其阈值由数据自身确定,LSSVM稀疏性降低的问题得到解决。
为了验证改进的LSSVM方法的准确性,引入受试者工作特征(receiver operating characteristic, ROC)曲线。图10为基于径向基核函数的LSSVM和改进的LSSVM方法的ROC曲线。由此可以看出改进的LSSVM方法对原LSSVM方法进行了优化,且效果明显。表3表示LSSVM测试数据训练结果。对于输入样本1,在经过正常的滚动轴承训练后,实际输出中只有第1个是正数,其输出结果为表3中的目标输出结果,因此判定轴承故障为正常。同理,另外3种测试样本的输出结果依次只有第2个、第3个、第4个值为正数,则判定这3种轴承故障依次为外圈故障、内圈故障和滚珠故障。其输出结果符合实际,故改进的LSSVM方法可以应用于实际的轴承故障诊断中,且输出结果可信。
5結论
针对最小二乘支持向量机在核参数选择上的盲目性、LSSVM方法的稀疏性欠缺的问题,提出了LMD形态滤波的LSSVM方法。该方法具有如下优点:
1)本文信号降噪、特征提取方式采用:LMD分解—相关分析—形态滤波降噪—信号重组—LMD再分解—特征提取,该方法能有效地去除噪声,提高特征向量的精确度;
2)通过研究特征向量走势和数据特点,提出新的核函数,实现了参数的自适应确定,解决了LSSVM参数难以选择的问题;
3)通过分析测量目标的结构特点,确定PF分量选取,降低了特征向量维度,减少了计算量以及在一定程度上降低了LSSVM的稀疏性;采用剪枝方法,提出了一种阈值确定方法,降低了LSSVM稀疏性差的问题;
4)LMD形态滤波LSSVM方法结构紧凑、算法简单,能有效解决轴承故障诊断问题。
参 考 文 献:
[1]SUYKENS J A K, VANDEWALLE J. Least Squares Support Vector Machine Classifiers[J]. Neural Processing Letters,1999, 9(3):293.
[2]满春涛, 刘博, 曹永成. 粒子群与遗传算法优化支持向量机的应用[J].哈尔滨理工大学学报,2019,24(3):87.
MAN Chuntao, LIU Bo, CAO Yongcheng. The Application Based on Support Vector Machine Optimized by Particle Swarm Optimization and Genetic Algorithm[J]. Journal of Harbin University of Science and Technology, 2019,24(3):87.
[3]ZHANG Zhen, ZHEN Chenggang. Research on Fault Diagnosis Method of Wind Turbine Based on CS and LSSVM[J]. International Core Journal of Engineering, 2019, 5(10):25.
[4]甘良志, 孫宗海, 孙优贤. 稀疏最小二乘支持向机[J], 浙江大学学报(工学版), 2007(2):245.
GAN Liangzhi, SUN Zonghai, SUN Youxian. Sparse Least Squares Support Vector Machine[J]. Journal of Zhejiang University (Engineering Science), 2007(2):245.
[5]张瑞, 李可, 宿磊, 等. 深度稀疏最小二乘支持向量机故障诊断方法研究[J].振动工程学报,2019,32(6):1104.
ZHANG Rui, LI Ke, SU Lei, et al. Fault Diagnosis Method of Deep Sparse Least Squares Support Vector Machine[J]. Journal of Vibration Engineering, 2019, 32(6):1104.
[6]HAN Minghong, WU Yaman, WANG Yumin, et al. Roller Bearing Fault Diagnosis Based on LMD and Multiscale Symbolic Dynamic Information Entropy[J]. Journal of Mechanical Science and Technology, 2021, 35(5):1993.
[7]张文斌, 杨辰龙, 周晓军. 形态滤波方法在振动信号降噪中的应用[J].浙江大学学报(工学版),2009,43(11):2096.
ZHANG Wenbin, YANG Chenlong, ZHOU Xiaojun. Application of Morphology Filtering Method in Vibration Signal Denoising [J]. Journal of Zhejiang University (Engineering Science),2009,43(11):2096.
[8]HAN Minghong, PAN Jiali. A Fault Diagnosis Method Combined with LMD, Sample Entropy and Energy Ratio for Roller Bearings. Measurement, 2015,76:7.
[9]DUAN Hao, LU Ming, SUN Yongteng, et al. Fault Diagnosis of PMSG Wind Power Generation System Based on LMD and MSE[J]. Complexity, 2020, 2020:11.
[10]CHEN Bingyan, SONG Dongli, ZHANG Weihua, et al. A Performance Enhanced Timevarying Morphological Filtering Method for Bearing Fault Diagnosis[J]. Measurement, 2021, 176:109163.
[11]宋海军, 黄传金, 刘宏超, 等. 基于改进LMD的电能质量扰动检测新方法[J].中国电机工程学报,2014,34(10):1700.
SONG Haijun, HUANG Chuanjin, LIU Hongchao, et al. A New Power Quality Disturbance Detection Method Based onthe Improved LMD[J]. Proceedings of the CSEE,2014,34(10): 1700.
[12]许同乐, 王营博, 郑店坤, 等. 基于LMDICA降噪的滚动轴承故障特征提取方法研究[J].北京邮电大学学报.2017(2):111.
XU Tongle, WANG Yingbo, ZHENG Diankun, et al. Research of the Rolling Bearing Fault Signal Feature Extraction Method Based on the LMDICA Noise Reduction[J]. Journal of Beijing University of Posts and Telecommunications. 2017(2):111.
[13]孙伟, 熊邦书, 黄建萍. 小波包降噪与LMD相结合的滚动轴承故障诊断方法[J].振動与冲击,2012,34(18):153.
SUN Wei, XIONG Bangshu, HUANG Jianping. Fault diagnosis of a Rolling Bearing Using Wavelet Packet Denoising and LMD[J]. Journal of Vibration and Shock,2012,34(18):153.
[14]张西宁, 唐春华, 周融通, 等. 一种自适应形态滤波算法及其在轴承故障诊断中的应用[J].西安交通大学学报,2018,52(12):1.
ZHANG Xi′ning, TANG Chunhua, ZHOU Rongtong, et al. Adaptive Morphological Filtering Algorithm with Applications in Bearing Fault Diagnosis[J]. Journal of Xi′an Jiaotong University,2018, 52(12):1.
[15]崔锡龙, 王红军, 邢济收, 等. 广义形态滤波和VMD分解的滚动轴承故障诊断[J].电子测量与仪器学报,2018,32 (4):51.
CUI Xilong, WANG Hongjun, XING Jishou, et al. Rolling Bearing Fault Diagnosis of Generalized Morphological Filtering and VMD Decomposition[J]. Journal of Electronic Measurement and Instrumentation,2018,32(4):51.
[16]PATEL J P, UPADHYAY S H. Comparison between Artificial Neural Network and Support Vector Method for a Fault Diagnostics in Rolling Element Bearings[J]. Procedia Engineering,2016,144:390.
[17]李永波, 徐敏强, 赵海洋, 等. 基于层次模糊熵和改进支持向量机的轴承诊断方法研究[J].振动工程学报,2016,29 (1):184.
LI Yongbo, XU Minqiang, ZHAO Haiyang, et al. Study on Rolling Bearing Fault Diagnosis Method Based on Hierarchical Fuzzy Entropy and ISVMBT[J]. Journal of Vibration Engineering,2016, 29(1):184.
[18]靳丽蕾, 杨文柱, 王思乐, 等. 一种用于卷积神经网络压缩的混合剪枝方法[J]. 小型微型计算机系统, 2018,39(12): 2596.
JIN Lilei, YANG Wenzhu, WANG Sile, et al. Mixed Pruning Method for Convolutional Neural Network Compression[J]. Journal of Chinese Computer Systems,2018,39(12):2596.
[19]HAN Fuxin, LI Yang, WANG Chensong. Multithreshold Channel Pruning Method Based on L1 Regularization[C]. England: Journal of Physics: Conference Series, 2021,1948(1): 012051.
[20]KAVITA Ml. An ApproachTowards Enhancement of Classification Accuracy Rate Using Efficient Pruning Methods with Associative Classifiers[J]. International Journal of Information Technology, 2021,1.
(编辑:温泽宇)

