哼唱检索中旋律特征的聚类与优化方法

王宁，陈晨，陈德运，何勇军

摘要：哼唱检索是音频检索的一个重要分支，其能够为用户提供一种方便快捷的全新体验。在检索过程中，由于同首歌的不同哼唱版本之间具有不容忽视的差异，因此对旋律特征进行精确匹配并无法得到理想的检索结果。针对这一问题，将基于优化初始聚类中心的kmeans（optimized initial clustering center kmeans， OICC kmeans）聚类方法引入到哼唱检索系统中，通过对旋律特征进行聚类来充分学习不同旋律特征之间的结构相似性，从而将具有相似结构的旋律特征划分到同一聚类内给聚类编号，以为后端的旋律特征匹配提供更有效的标签。同时，考虑到聚类后的旋律特征可以进行进一步的特征表示，因此将聚类后的标签作为深度置信网络（deep belief networks， DBN）的输入标签并进行特征提取，以获取具有更强区分性的高层旋律特征，从而有效提升旋律特征的鲁棒性。在获取高层旋律特征后，需将聚类类别作为匹配标签，并进行哼唱检索即可。实验结果表明所提出的方法能够有效提升哼唱检索系统的性能。

关键词：哼唱检索;旋律特征提取;kmeans聚类算法;深度置信网

DOI：10.15938/j.jhust.2022.01.009

中图分类号： TP391.3         文献标志码： A          文章编号： 1007-2683（2022）01-0061-08

Melody Feature Clustering and Optimization for Querybyhumming

WANG Ning，CHEN Chen，CHEN Deyun，HE Yongjun

（School of Computer Science and Technology， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：Querybyhumming is an important branch of audio retrieval， and it can provide users with a new and convenient experience. During the retrieval process， since there are unignorable differences between different humming of the same song， it is difficult to obtain ideal results by accurate matching of the melody features. To solve this problem， the optimized initial clustering center kmeans （OICC kmeans） is introduced in the querybyhumming system. By clustering melody features to fully learn the structural similarity between different melody features， the melody features with similar structures are divided into the same cluster and the clusters are numbered， so as to provide more effective matching of melody features at the back end label. Meanwhile， considering that the clustered melody features can be further characterized， the clustered tags are used as the input tags of deep belief networks （DBN） and feature extraction is performed to obtain stronger discriminative characteristics the highlevel melody features of the melody， thereby effectively improving the robustness of melody features. After obtaining the highlevel melody features， it is necessary to use the cluster category as a matching tag and perform a humming search. Experimental results show that the proposed method can effectively improve the performance of humming retrieval system.

Keywords：querybyhumming; melody segmentation; kmeans clustering algorithm; deep belief network

0引言

哼唱檢索是近年来新兴的检索方法，是一项通过哼唱歌曲来进行音乐检索的技术[1]。具体而言，哼唱检索需要检索出与哼唱旋律特征相匹配的歌曲旋律特征，从而根据旋律特征的匹配程度来确定哼唱歌曲的所属类别。然而，不同人哼唱同一旋律将会产生较大差异，从而导致同首歌在不同版本之间的旋律特征具有极强的不一致性[2]。因此，并无法保证哼唱歌曲与其对应歌曲的旋律特征完全一致，进而导致检索结果不准确。针对这一问题，往往需要采用近邻检索方法[3]，将与哼唱旋律特征空间距离较近的歌曲旋律特征当作候选集，从而尽可能保证正确检索结果涵盖于其中。研究者们针对旋律匹配问题，相继提出很多近邻检索算法。文[4-6]首先尝试了动态时间归整（dynamic time warping， DTW）与线性伸缩（linear scaling， LS）等近邻检索算法。接着，文[7]提出了一种具有优越性的递归对齐（recursive align， RA）方法。而文[8-9]提出的局部敏感哈希（locality sensitive hashing， LSH）方法则是目前应用最为广泛的近邻检索方法。LSH通过随机选定投影方向，将高维空间中的数据映射到一维空间，从而有效缩短检索时间。然而，这种随机性投影并不稳定，数据集的改变将导致检索精度随之变化，且检索系统无法动态地调整参数来适应数据集变化。同时，由于LSH方法需要通过旋律特征在多个方向上的投影来获取近邻，因此并无法保证其得到的近邻候选集是旋律特征的真正近邻。

针对上述问题，可以直接在特征空间中对旋律特征进行聚类，将空间距离近的旋律特征划分到同一聚类，使得划分到同一聚类内的旋律特征均互为真正近邻，从而有效保证检索结果的正确性。此外，在建立歌曲库索引时，聚类方法只需要记录所属聚类标签即可。相比于需要使用多个哈希函数来建立索引的LSH方法，聚类方法不仅简单高效，且占用资源更少。在众多旋律特征聚类方法中，使用最广泛的方法为k-均值聚类算法（kmeans）[10]。其首先需要随机选取K个初始簇类中心，然后将全部旋律特征按规则划分为K个簇，从而保证簇内旋律特征相似度较高、簇间相似度较低。虽然kmeans算法简单高效，但随机选取初始聚类中心将引入更多的不确定因素，且易陷入局部最优解。针对这一问题，kmeans++算法[11]通过预先处理离群近点来提高迭代速度，而迭代自组织数据分析算法（iterative selforganizing data analysis techniques algorithm， ISODATA）[12]则通过合并与分裂的方式，来进行聚类数k的合理估计。尽管上述方法能够取得较好的性能，但没有充分考虑数据集密度分布不均匀的情况，对于密度差异较大的数据集处理效果并不理想。

针对kmeans算法初始簇心敏感和无法很好处理密度差异较大的数据集问题，本文将优化初始聚类中心的kmeans（optimized initial clustering center kmeans， OICC kmeans）算法[13-14]引入到哼唱检索中，其能够依据高密度优先聚类的思想，有效提升密度差异较大数据集的聚类效果，还能增强算法的稳定性。经过特征聚类后，同簇的旋律特征具有更高的结构相似性。对旋律特征进行聚类后，本文将聚类结果作为标签，并采用深度置信网络（deep belief networks， DBN）[15-16]，来进行旋律特征提取，以获得区分性更强的高层旋律特征。进行哼唱检索时，利用哼唱旋律特征匹配到最相似的聚类特征，在该聚类内的歌曲旋律特征结构相似，正确检索结果包含在其中。因此，在该类内检索即可得到准确检索结果，使得该系统不仅检索稳定高效，而且检索精度高。

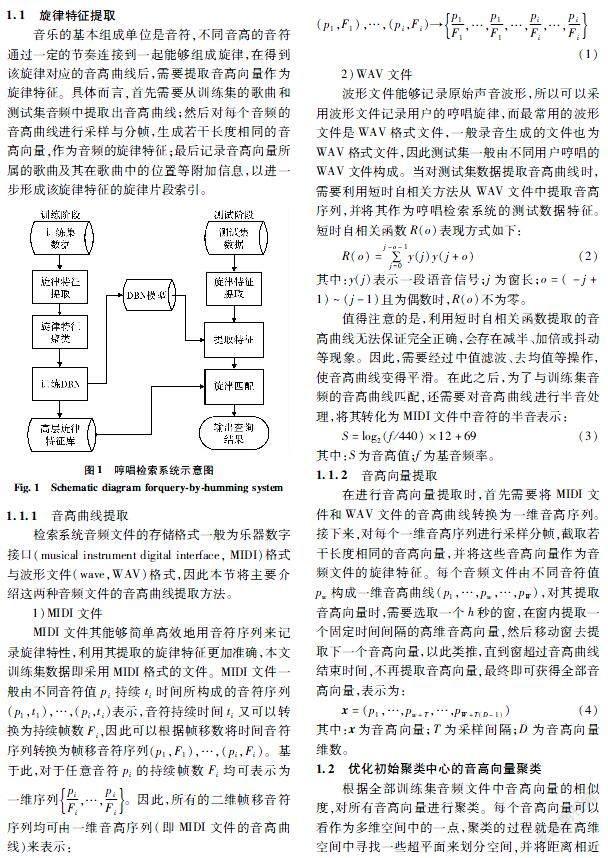
1基于OICC kmeans與DBN的哼唱检索系统

本节将介绍基于OICC kmeans与DBN的哼唱检索方法[17]。首先，需要对训练数据进行旋律特征提取，该特征为音高向量;其次，对音高向量进行聚类并利用聚类标签训练DBN网络;再次，利用训练好的DBN模型对测试数据提取特征;最后，与训练集旋律特征库中的旋律特征进行匹配并找到所属类别，在类内继续匹配输出检索结果，其示意图如图1所示。

1.1旋律特征提取

音乐的基本组成单位是音符，不同音高的音符通过一定的节奏连接到一起能够组成旋律，在得到该旋律对应的音高曲线后，需要提取音高向量作为旋律特征。具体而言，首先需要从训练集的歌曲和测试集音频中提取出音高曲线;然后对每个音频的音高曲线进行采样与分帧，生成若干长度相同的音高向量，作为音频的旋律特征;最后记录音高向量所属的歌曲及其在歌曲中的位置等附加信息，以进一步形成该旋律特征的旋律片段索引。

1.1.1音高曲线提取

检索系统音频文件的存储格式一般为乐器数字接口（musical instrument digital interface， MIDI）格式与波形文件（wave，WAV）格式，因此本节将主要介绍这两种音频文件的音高曲线提取方法。

1）MIDI文件

MIDI文件其能够简单高效地用音符序列来记录旋律特性，利用其提取的旋律特征更加准确，本文训练集数据即采用MIDI格式的文件。MIDI文件一般由不同音符值pi持续ti时间所构成的音符序列（p1，t1），…，（pi，ti）表示，音符持续时间ti又可以转换为持续帧数Fi，因此可以根据帧移数将时间音符序列转换为帧移音符序列（p1，F1），…，（pi，Fi）。基于此，对于任意音符pi的持续帧数Fi均可表示为一维序列piFi，…，piFi。因此，所有的二维帧移音符序列均可由一维音高序列（即MIDI文件的音高曲线）来表示：

（p1，F1），…，（pi，Fi）→p1F1，…，p1F1，…，piFi，…，piFi（1）

2）WAV文件

波形文件能够记录原始声音波形，所以可以采用波形文件记录用户的哼唱旋律，而最常用的波形文件是WAV格式文件，一般录音生成的文件也为WAV格式文件，因此测试集一般由不同用户哼唱的WAV文件构成。当对测试集数据提取音高曲线时，需要利用短时自相关方法从WAV文件中提取音高序列，并将其作为哼唱检索系统的测试数据特征。短时自相关函数R（o）表现方式如下：

R（o）=∑j-o-1j=0y（j）y（j+o）（2）

其中：y（j）表示一段语音信号;j为窗长;o=（-j+1）～（j-1）且为偶数时，R（o）不为零。

值得注意的是，利用短时自相关函数提取的音高曲线无法保证完全正确，会存在减半、加倍或抖动等现象。因此，需要经过中值滤波、去均值等操作，使音高曲线变得平滑。在此之后，为了与训练集音频的音高曲线匹配，还需要对音高曲线进行半音处理，将其转化为MIDI文件中音符的半音表示：

S=log2（f/440）×12+69（3）

其中：S为音高值;f为基音频率。

1.1.2音高向量提取

在进行音高向量提取时，首先需要将MIDI文件和WAV文件的音高曲线转换为一维音高序列。接下来，对每个一维音高序列进行采样分帧，截取若干长度相同的音高向量，并将这些音高向量作为音频文件的旋律特征。每个音频文件由不同音符值pw构成一维音高曲线（p1，…，pw，…，pW），对其提取音高向量时，需要选取一个h秒的窗，在窗内提取一个固定时间间隔的高维音高向量，然后移动窗去提取下一个音高向量，以此类推，直到窗超过音高曲线结束时间，不再提取音高向量，最终即可获得全部音高向量，表示为：

x=（p1，…，pw+T，…，pW+T（D-1））（4）

其中：x为音高向量;T为采样间隔;D为音高向量维数。

1.2优化初始聚类中心的音高向量聚类

根据全部训练集音频文件中音高向量的相似度，对所有音高向量进行聚类。每个音高向量可以看作为多维空间中的一点，聚类的过程就是在高维空间中寻找一些超平面来划分空间，并将距离相近

的点放在同一个局域内，从而不同区域内的音高向量构成了不同的旋律聚类。

kmeans算法在数据集上随机选取K个数据对象作为初始聚类中心，但其随机性较强，会导致聚类效果不稳定。针对这一问题，考虑到特征空间中相同尺度区间内包含的数据越多，这一区间的数据密度越大，在这一区间内则更可能存在聚类中心。基于此，可以通过划分密度集合区间，并在各个集合区间选取初始聚类中心，来寻找更合适的聚类中心。同时，根据密度选取的聚类中心一般具有唯一性，能够有效降低由初始中心的随机性选取所带来的影响。

基于上述思想，本文对音高向量特征空间中的不同密度区域进行划分，首先从音高向量集合中取欧氏距离最小的一对组成簇类，计算簇类均值并记为该簇的簇类中心。然后从剩余音高向量集合中选取距离簇类中心最近的音高向量，将其加入该簇并更新簇类中心，重复以上步骤直到簇类中音高向量的数量达到阈值。每当获得一个簇类，便重复上述过程直到簇类数量为K时结束。

依据上述步骤，能够获取更准确的初始聚类中心。定义音高向量的数据集合为X={x1，…，xn，…，xN}（n∈1，2，…，N），N为音高向量个数;簇类集合Z={Z1，…，Zk，…，ZK}，簇类中心集合为C={C1，…，Ck，…，CK}（k∈1，2，…，K），K为簇类的数量。根据上述符号定义，首先应该计算两个音高向量的欧式距离：

d（xa，xb）=∑Ll=1（xal-xbl）2（a，b=1，2，…，L）（5）

其中：xa，xb为音高向量;xal为xa的第l个特征属性;xbl为xb的第l个特征属性。接着将距离最短的两个音高向量组成一个簇类集合Zk，并从数据集X中将上述音高向量删除，将更新后的数据集记为X′，同时计算样本集合Zk内所有音高向量的均值CZk。

然后，计算数据集X中每个音高向量xn与样本集合Zk对应均值CZk的距离：

dist=∑xn∈X′d（xn，CZk）（6）

找到距离最近的音高向量加入集合Zk，将其从数据集X′中删除，并重新计算集合Zk内所有数据对象的均值。重复执行直致Zk内音高向量的个数大于等于α·（N/K），其中α为权重系数，且0<α≤1。若k<K，则重复以上步骤直到k≥K，即当集合的数目等于簇类数目时，结束寻找初始聚类中心。

经过上述步骤即可获得最优的初始聚类中心，利用这些聚类中心进行音高向量聚类从而获得最优聚类结果。音高向量集X={x1，…，xn，…，xN}，每个数据对象xn有D维，在半径R内数据对象数目与总数据集的比值（占比率）为P（0≤P≤1），相邻两次误差平方和之差为β，则改进算法的详细描述如算法1所示。

算法1优化初始聚类中心的kmeans聚类算法

Algo.1Optimizing initial clustering center for kmeans clustering algorithm

Input：X={x1，…，xn，…，xN}：数据集;K：簇类数目;

P：占比率;β：相邻两次误差平方和之差

Output：聚类结果

1 利用优化的初始聚类方法获得K个聚类中心作为初始中心;

2 for 聚类中心不再变化or连续两次E值差小于阈值 do

[计算每个数据对象与中心的距离：

E=∑Kk=1∑xn∈Ckd（xn，Ck）

并把它划分给最近的聚类中心，得到K个簇类;

重新计算每个簇类的中心：

s=∑xb∈CKd（xa，xb）（xa∈X）;

重新划分簇并更新中心;

]

3 输出：聚类后的簇

通过此算法对音高向量进行聚类后，同一聚类内的音高向量结构特征极其相似，可以用相似的特征来表示这个聚类，在检索时找到與哼唱旋律特征相似的聚类，即可得到全部候选集，只需在聚类内检索即可得到检索结果。此外，为了获得区分性更强的高层旋律特征，需要将旋律特征作为输入来训练DBN，标签则采用聚类后簇的标号。

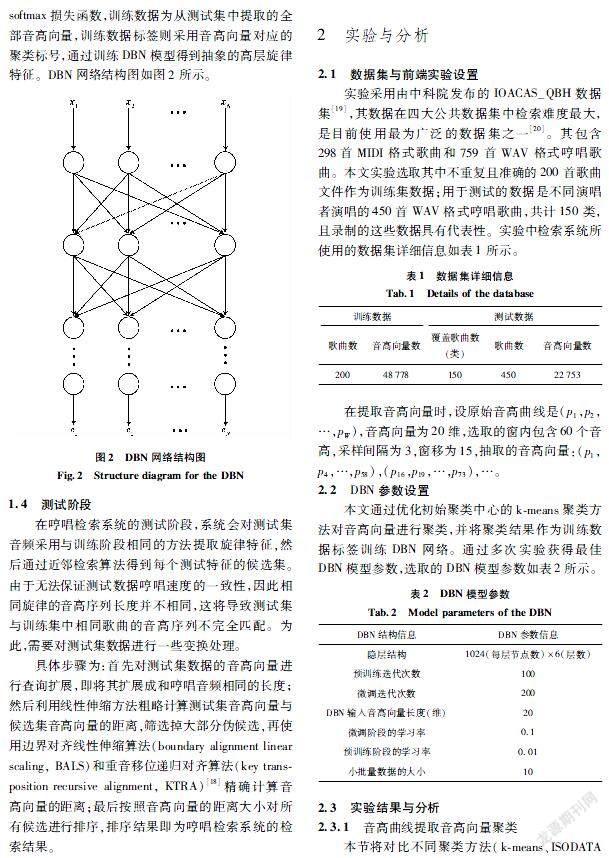
1.3深度置信网络训练

在训练深度置信网络时，需要用到训练集的音高向量{x1，x2，…，xN}和所属聚类标签两部分信息，用于提取抽象高层旋律特征{e1，e2，…，eN}。在训练过程中采用sigmoid激活函数，目标函数则采用softmax损失函数，训练数据为从测试集中提取的全部音高向量，训练数据标签则采用音高向量对应的聚类标号，通过训练DBN模型得到抽象的高层旋律特征。DBN网络结构图如图2所示。

1.4测试阶段

在哼唱检索系统的测试阶段，系统会对测试集音频采用与训练阶段相同的方法提取旋律特征，然后通过近邻检索算法得到每个测试特征的候选集。由于无法保证测试数据哼唱速度的一致性，因此相同旋律的音高序列长度并不相同，这将导致测试集与训练集中相同歌曲的音高序列不完全匹配。为此，需要对测试集数据进行一些变换处理。

具体步骤为：首先对测试集数据的音高向量进行查询扩展，即将其扩展成和哼唱音频相同的长度;然后利用线性伸缩方法粗略计算测试集音高向量与候选集音高向量的距离，筛选掉大部分伪候选，再使用边界对齐线性伸缩算法（boundary alignment linear scaling， BALS）和重音移位递归对齐算法（key transposition recursive alignment， KTRA）[18]精确计算音高向量的距离;最后按照音高向量的距离大小对所有候选进行排序，排序结果即为哼唱检索系统的检索结果。

2实验与分析

2.1数据集与前端实验设置

实验采用由中科院发布的IOACAS_QBH数据集[19]，其数据在四大公共数据集中检索难度最大，是目前使用最为广泛的数据集之一[20]。其包含298首MIDI格式歌曲和759首WAV格式哼唱歌曲。本文实验选取其中不重复且准确的200首歌曲文件作为训练集数据;用于测试的数据是不同演唱者演唱的450首WAV格式哼唱歌曲，共计150类，且录制的这些数据具有代表性。实验中检索系统所使用的数据集详细信息如表1所示。

在提取音高向量时，设原始音高曲线是（p1，p2，…，pW），音高向量为20维，选取的窗内包含60个音高，采样间隔为3，窗移为15，抽取的音高向量：（p1，p4，…，p58），（p16，p19，…，p73），…。

2.2DBN参数设置

本文通过优化初始聚类中心的kmeans聚类方法对音高向量进行聚类，并将聚类结果作为训练数据标签训练DBN网络。通过多次实验获得最佳DBN模型参数，选取的DBN模型参数如表2所示。

2.3实验结果与分析

2.3.1音高曲线提取音高向量聚类

本节将对比不同聚类方法（kmeans、ISODATA kmeans、kmeans++）与本文所采用方法（OICC kmeans）的聚类效果。在音高向量聚类实验中，采用相同音高向量数据集，通过4种不同的kmeans聚类算法测试聚类性能的差异。对不同的kmeans聚类方法进行相同的聚类测试，并采用类内平方和（withincluster sum of squares， WCSS）[21]作为聚类效果的度量标准。

待聚类的音高向量集X={x1，…，xn，…，xN}，其中N为待聚类向量的数量，设每个向量的长度为D，聚类数设定为K（K≤N），最终得到的K个聚类为C={C1，…，Ck，…，CK}，那么WCSS为：

WCSS（C）=∑Kr=1∑xr∈Cr||xr-μr||2（7）

其中，μr是聚类Cr的均值点，设Cr中的向量数为vr，那么：

μr=1vr∑xr∈Crxr（8）

此外，音高向量间的欧式距离由式（5）来计算得出。

在进行音高向量聚类实验时，采用表1训练数据作为测试集。为排除1组实验结果的偶然性，随机地将200个训练数据平分成2组，对每组数据采用不同聚类方法。实验结果如表3所示。

在上表中，每列代表1个组别，每个组别内设定相同的聚类数，采用不同的聚类方法在该组数据集上进行实验，依次得到不同聚类方法对应的WCSS值，这个值越小证明类内的平均距离越小，类间的距离越大，聚类的效果越好。为了避免kmeans初始化过程随机不稳定对实验结果的影响，所以需要对每组实验重复实验5次，通过取平均值得到最终的结果。

观察实验结果可以得知，在相同数据集下进行相同测试，本文算法（IOCC kmeans）的WCSS值最小，说明该算法比kmeans、ISODATA+kmeans和kmeans++聚类效果更好，可以获得最优的音高向量聚类。

2.3.2哼唱检索

哼唱检索系统的检索结果为与测试音频相似度最大的前5首候选歌曲。评价指标采用Top-1正确率（Accuracy，ACC）与Top-5正确率：

ACC（Top-1）=∑Gg=11{Eg=Pgu}G（9）

ACC（Top-5）=∑Gg=11∑5j=11{Eg=Pgu}G（10）

其中：G為待检索哼唱音频数;Pgu为对于第g个查询的第u个检索结果;Eg表示第g个查询的正确检索结果。1{Eg=Pgu}为一个指示器，在满足大括号内的条件时，该式的值为1，否则值为0。依据正确率评价指标，对使用不同的kmeans聚类算法结合DBN实现的哼唱检索方法进行性能对比，并使用基于LSH的哼唱检索算法作为对照。同时，考虑到卷积神经网络具有强大的特征提取能力，因此本文加入CNN作为DBN的对比实验[22]。

本文输入网络的特征为一维音高向量，因此，只能采用一维卷积提取高层旋律特征，同时音高向量为20维，避免卷积核过大而丢失掉局部特征信息，实验采用大小为3的卷积核，通过多次实验获得最佳CNN模型参数。CNN网络采用三层卷积结构，卷积核数量分别为32、64和128，卷积核大小均为3×1，每层卷积之后连接Batch Normalization层，用来实现批量归一化以加速训练，之后接入ReLU作为激活特征层，前一层卷积层的输出作为后一层的输入，最后目标函数则采用softmax损失函数。不同方法的实验结果如表4所示。

根据上述实验结果显示，在相同训练集以及相同测试集情况下，基于优化初始聚类中心的kmeans聚类哼唱检索算法优于其他3种kmeans聚类的哼唱检索算法，而且本文算法的检索精度也优于基于LSH的检索算法和OICC kmeans结合CNN的哼唱检索算法。同时，本文算法在其他诸多方面实现了优化。

首先改进的kmeans聚类算法对音高向量聚类效果最优，为DBN训练提供准确标签，从而达到最优检索精度。其次当数据集发生变化时，基于LSH的哼唱检索算法无法动态地调整参数应对变化，而本文哼唱检索算法可以利用新数据集重新训练DBN网络模型来更新系统参数，能很好的适应数据集变化。

2.3.3旋律特征可视化对比

为了验证本文提出方法的有效性，本节将通过可视化的方式来对比OICC kmeans分别结合DBN

与CNN的哼唱检索算法。对于实验数据的选择，考虑到测试数据没有聚类标签，原始数据无法2D可视化表示，因此本节实验可视化的数据均来自于开发集。随机选择7类音频，并从每类中随机选择200段（若该类音频段数少于200，则不会选择该类数据），不同方法均采用以上标准选择出的数据进行可视化，上述方法对应的可视化结果如图3所示，不同颜色的点代表不同类别音频。将所对比方法的旋律特征分别记为音高向量特征、CNN特征与DBN特征。根据图3可以得到以下结论。

1）在圖3（a）中，由于原始音高向量通过OICC kmeans聚类后，已经具有表征该类旋律特征的能力，因此图中相同类别音高向量的数据能够聚集在一起，不同类别音高向量的数据能够相互区分开，只是同类数据仍然较分散，不同类数据之间的混杂程度仍然较高。

2）在图3（b）中，通过CNN提取的旋律特征与原始音高向量相比，同类的数据能够较好的聚集在一起，异类数据之间的距离较分散。但是，2个方框中的数据虽然属于同类，却被分为2个簇，CNN仍然没有解决部分特征错分类别问题。

3）在图3（c）中，与前两种旋律特征相比，通过DBN提取的旋律特征能够更好的相互区分开：同类数据更聚集，异类数据更分散。同时，不存在图3（b）中方框中的情况，数据被正确的划分到同一簇类中。由此可见，DBN能够提取区分性更强的高层旋律特征。

3结语

针对邻近检索不准确问题，本文提出了一种基于旋律特征聚类与优化的哼唱检索方法。首先该方法对音高向量进行聚类，使得同一聚类内的音高向量互为准确的近邻，从而有效地解决了近邻检索不准确的问题。相对传统kmeans聚类算法，本文采用优化初始聚类中心的kmeans算法使得哼唱检索系统在近邻检索效果方面有显著提升。然后通过DBN网络对音高向量进行旋律特征提取，得到区分性更强的高层旋律特征，比传统方法获取的旋律特征更加稳定可靠。实验结果表明，本文提出的哼唱检索系统不仅性能优越，而且检索稳定，其能够动态调整系统参数去应对数据集变化，综合表现较之前的哼唱检索系统更加优秀。

参 考 文 献：

[1]GHIAS A， LOGAN J， DAVID C， et al. Query by Humming： Musical Information Retrieval in an Audio Database[C] // Multimedia95： Third Acm International Conference on Multimedia， 1995： 231.

[2]ZHANG W W， WANG R， ZHANG Q L，et al. A Joint Pitch Estimation and Voicing Detection Method for Melody Extraction[J]. Applied Acoustics， 2020， 166：107338.

[3]PAN Z B， Wang L Z， Wang Y， et al. Product Quantization with Dual Codebooks for Approximate Nearest Neighbor Search[J]. Neurocomputing， 2020， 401：59.

[4]JANG J S R， GAO M Y. A QuerybySinging System Based on Dynamic Programming[C] // International Workshop Intelligent Systems Resolutions， 2000： 85.

[5]LI H H， LIU J X， YANG Z L，et al. Adaptively Constrained Dynamic Time Warping for Time Series Classification and Clustering[J]. Information Sciences， 2020， 534：97.

[6]JANG J S R， LEE H R， KAO M Y. Contentbased Music Retrieval Using Linear Scaling and Branchandbound Tree Search[C] // The IEEE International Conference on Multimedia and Expo. IEEE， 2001： 289.

[7]WU X， LI M， LIU J， et al， A Topdown Approach to Melody Match in Pitch Contour for Query by Humming[C] // International Conference of Chinese Spoken Language Processing. IEEE， 2006： 669.

[8]RYYNANEN M， KLAPURI A. Query by Humming of MIDI and Audio Using Locality Sensitive Hashing[C] // 2008 IEEE International Conference on Acoustics， Speech and Signal Processing. IEEE， 2008： 2249.

[9]LI Y Q， XIAO R L， WEI X， et al. GLDH： Toward More Efficient Global Lowdensity Localitysensitive Hashing for High Dimensions[J]. Information Sciences， 2020， 533：43.

[10]ENGLAND R， BEYNON D. Remark AS R39： A Remark on AS 136： A kmeans Clustering Algorithm[J]. Journal of the Royal Statistical Society. Series C （Applied Statistics）， 1981， 30（3）： 355.

[11]ARTHUR D， VASSILVITSKII S. kmeans++： the Advantages of Careful Seeding[C] // Conference： Proceedings of the Eighteenth Annual ACMSIAM Symposium on Discrete Algorithms.IEEE， 2007： 1027.

[12]BALL G H， HALL D J， ISODATA， a Novel Method of Data Analysis and Pattern Classification[M]. California： Technicalrept， 1965：3.

[13]ZHONG W， GUIQUAN L， ENHONG C. A Kmeans Algorithm Based on Optimized Initial Center Points[J]. Pattern Recognition and Artificial Intelligence， 2009， 22（2）：299.

[14]韩剑辉， 唐俊超. 空间约束密度聚类的超像素分割算法[J]. 哈尔滨理工大学学报， 2020： 25（6）：6.

HANG Jianhui， TANG Junchao. Superpixel Segmentation Algorithm Based on Spatial Constrained Density Clustering[J].Journal of Harbin University of Science and Technology， 2020： 25（6）：6.

[15]HINTON G， OSINDERO S， TEH Y W. A Fast Learning Algorithm for Deep Belief Nets[J].Neural Computation， 2006， 18（7）：1527.

[16]王衛兵， 张立超， 徐倩. 一种基于受限波尔兹曼机的推荐算法[J]. 哈尔滨理工大学学报， 2020， 25（5）：66.

WANG Weibing， ZHANG Lichao， XU Qian. A Recommendation Algorithm Based on Restricted Boltzmann Machine[J].Journal of Harbin University of Science and Technology， 2020： 25（5）：66.

[17]曹亮. 海量音乐的哼唱检索研究[D]. 北京：北京邮电大学， 2015：22.

[18]GUO Z Y， WANG Q， LIU G，et al. A Query by Humming System Based on Locality Sensitive Hashing Indexes[J]. Signal Processing， 2013， 93（8）：2229.

[19]DOWNIE J S， WEST K， EHMANN A F， et al. The 2005 Music Information Retrieval Evaluation Exchange （MIREX 2005）： Preliminary Overview[C] // International Conference on Ismir. DBLP， 2005：320.

[20]HARTIGAN J A， WONG M A. Algorithm A S 136： A KMeans Clustering Algorithm[J]. Applied Statistics， 1979， 28（1）： 100.

[21]HARTIGAN J A， WONG M A. Algorithm AS 136： A Kmeans Clustering Algorithm[J]. Applied Statistics， 1979： 28（1）：100.

[22]李兰英， 周志刚， 陈德运. DBN和CNN融合的脱机手写汉字识别[J]. 哈尔滨理工大学学报， 2020： 25（3）：7.

LI Lanying， ZHOU Zhigang， CHEN Deyun. Offline Handwritten Chinese Character Recognition Based on the Integration of DBN and CNN[J].Journal of Harbin University of Science and Technology， 2020： 25（3）：7.

（编辑：温泽宇）