基于表面粗糙度的铝合金材料疲劳寿命预测
杨永康 杨亚莉 付仁杰






摘 要:为了研究表面粗糙度对铝合金材料疲劳寿命的影响,提出一种利用基于表面粗糙度曲线的插值法构造试件真实表面形貌的方法。首先对试件进行打磨处理,然后利用粗糙度仪提取打磨后试件的粗糙表面轮廓曲线;使用插值法重构三维有限元模型并进行疲劳寿命分析;将得到的疲劳寿命与MTS疲劳试验得到的结果相对比;最后建立了粗糙度参数与疲劳寿命之间的函数关系。结果表明:使用插值法得到的仿真疲劳寿命与试验得到的疲劳寿命结果基本一致,最大误差为19.2%,证明了该方法的正确性。粗糙度参数与疲劳寿命存在幂函数关系,基于粗糙度参数可开展疲劳寿命预测。
关键词:表面粗糙度;插值法;疲劳试验;寿命预测
中图分类号:TP304 文献标识码:A
Fatigue Life Prediction of Aluminum Alloy Materials based on Surface Roughness
YANG Yongkang, YANG Yali, FU Renjie
(School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China)
Abstract: In order to study the effect of surface roughness on the fatigue life of aluminum alloy materials, this paper proposes a method to construct real surface morphology of the test piece based on the interpolation method of the surface roughness curve. Firstly, the test piece is polished, and then the rough surface profile curve of the polished test piece is extracted with a roughness meter. Interpolation is used to reconstruct a three-dimensional finite element model and perform fatigue life analysis. Obtained fatigue life is compared with the results obtained from the MTS fatigue test. Finally, the functional relationship between roughness parameters and fatigue life is established. Results show that the simulated fatigue life obtained by the interpolation method is basically consistent with the fatigue life results obtained by the test. The maximum error is 19.2%, which proves the correctness of the method. There is a power function relationship between roughness parameters and fatigue life, and fatigue life prediction can be carried out based on roughness parameters.
Keywords: surface roughness; interpolation method; fatigue test; life prediction
1 引言(Introduction)
隨着汽车、船舶、航空航天等行业的发展,材料缺陷对疲劳寿命的研究成为时下热点。研究表明,构件表面存在的缺陷在交变载荷作用下极易造成应力集中,导致材料损伤直至断裂失效[1-2]。为此,许多研究人员对表面粗糙度与疲劳性能的关系进行了深层次研究。SURARATCHA等[3]对航用铝合金进行了有限元建模与计算,发现粗糙度的增加可以迅速降低材料疲劳性能。赵丙峰等[4]研究了不同部位粗糙度值对疲劳性能的影响差异。结果表明,不同缺口处的应力不同,造成构件疲劳性能不同,减缓粗糙度能够有效延长部件寿命周期。
通过特定的技术方法实现材料表面重构,可以在不消耗大量时间和成本的基础上还原真实表面形貌,获取疲劳数据。基于有限元分析方法,杨国庆等[5]研究了不同统计特征的接触粗糙表面的受力情况。利用3D粗糙表面的数字化手段,重构带有粗糙表面的有限元模型,分析了接触疲劳性能现象。唐兵[6]基于蒙特卡洛法重构了多种函数表面粗糙度模型,实现了各种随机粗糙度的重构。梅倩倩[7]使用粗糙度参数算法原理和高斯滤波法对表面粗糙度信息进行提取,将结果与实验测量结果进行比较,结果表明该方法具有较高的可行性和正确性。郑清春[8]使用有限元与数理统计回归方法证明保证残余应力相同时表面粗糙度越大,疲劳寿命越低。
上述研究仅仅讨论了粗糙度降低疲劳性能,以及通过应力集中变量考虑其影响,并没有对二者之间的联系进行阐述。因此本文将采用插值法重构损伤试件表面模型,并分析表面粗糙度对零件寿命的影响,从而建立粗糙度与疲劳寿命的函数关系,实现对疲劳寿命的预测。
2 试验(Experiment)
2.1 试件制备与固定
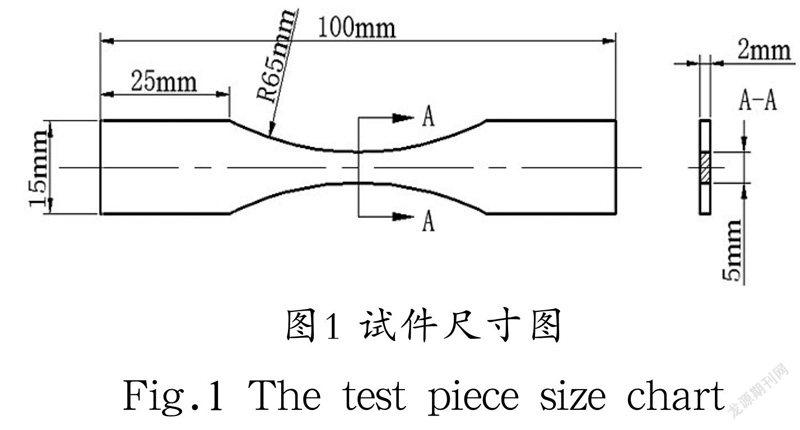
本试验所用的材料为6061-T6铝合金。试件按照美国试验材料学会ASTM E8/E8M-15a标准及《金属材料轴向等幅低循环疲劳试验方法》(GB/T 15248—2008)等国家标准的要求进行制作并对试件进行抛光处理[9]。试件的尺寸如图1所示。
将试件按照如图2所示的方式固定住,保证试件在同一水平。将一组打磨试件的首尾分别固定一个试件,在起到支撑作用的同时也避免了因受力不均匀产生的误差。两个固定试件在图2中的0号位置。
2.2 试件的打磨方案
本试验使用的设备是手提式砂带机BS6-100,如图3所示。该仪器方便更换砂纸和试件,也为后期打磨试验提供稳定的加工工艺。砂带机的基本参数是:频率为50 Hz;垫子尺寸为100 mm×610 mm,共有六个调速档位,转速从210 r/min—
440 r/min可供选择。为保证打磨过程的稳定性和打磨试件的一致性,统一设置打磨参数。本次打磨转速为210 m/min,打磨压力为5 N,打磨时间为2 min。设置四组试件,前两组轴向打磨,分别使用80 号、120 号砂纸;后两组周向打磨,分别使用240 号、400 号砂纸。打磨试验获取了拥有不同表面粗糙度的试件,如图4所示。
2.3 疲劳试验
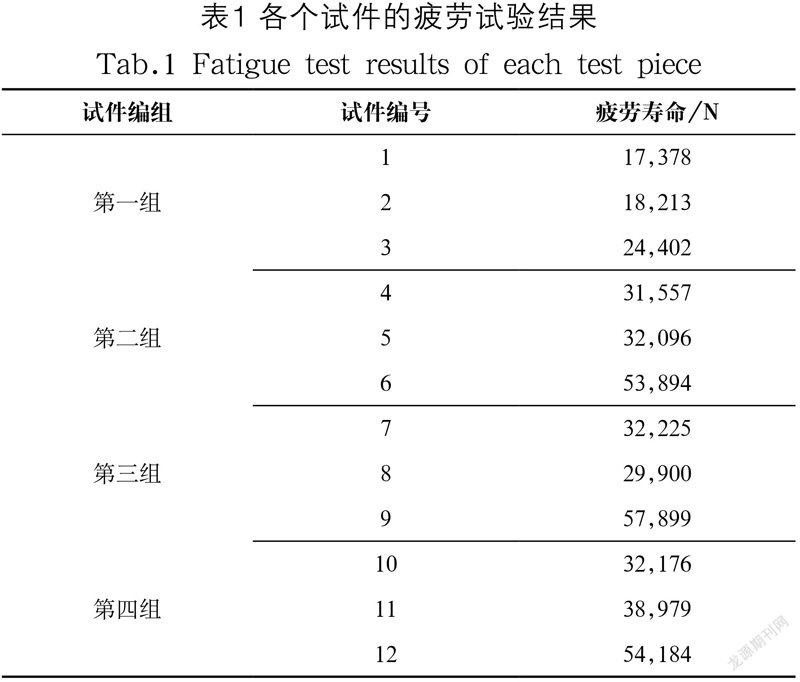
在电液伺服疲劳试验机上开展本次疲劳试验。采用单轴拉伸-拉伸循环加载,试验加载波形为正弦波。在应力比R=0.1、频率f=50Hz、载荷值F=3,100 N的条件下进行疲劳加载试验。试验结果如表1所示。
3 模型的重构与验证(Model reconstruction and validation)
3.1 表面粗糙度曲线的获取
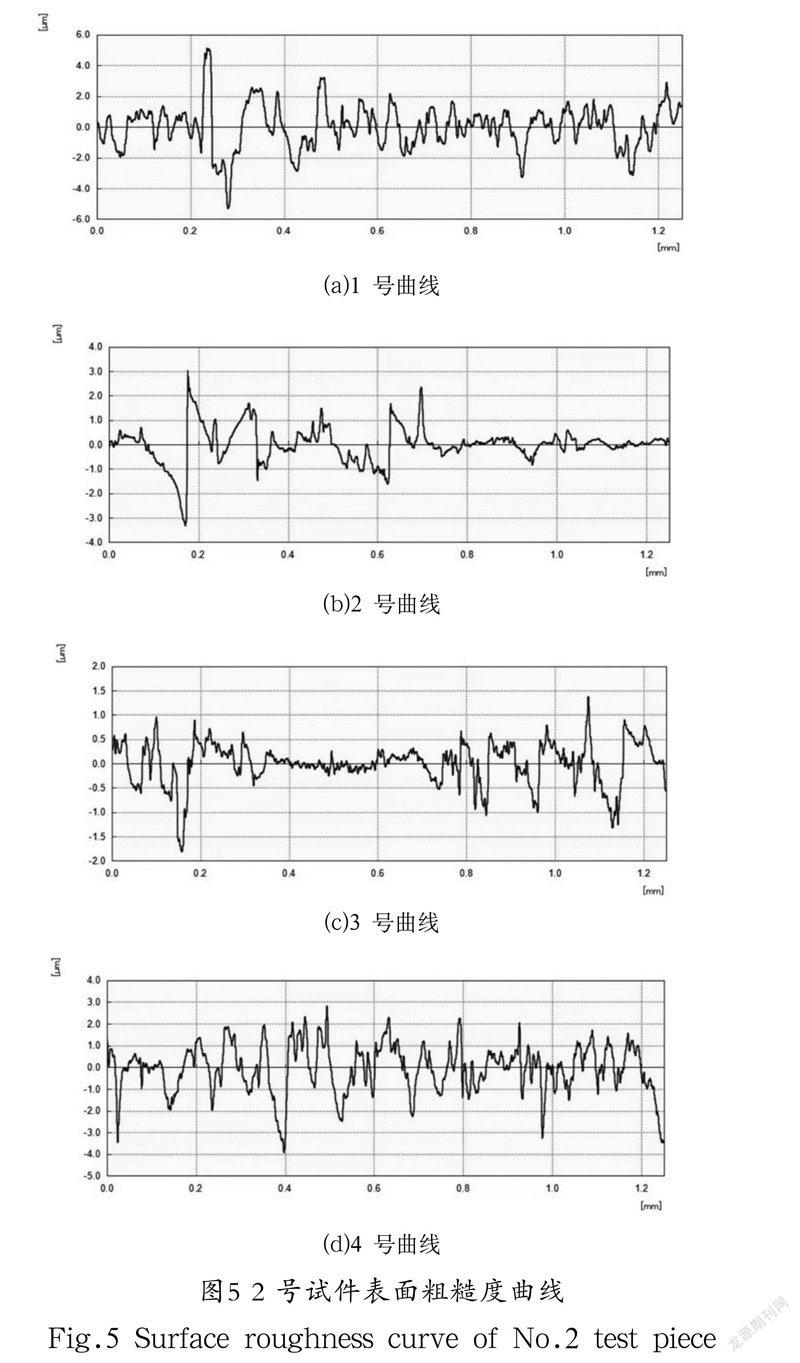
使用SJ-210粗糙度仪提供的SJ简单通信软件提取打磨后试件的表面粗糙度曲线[10]。从试件的中间部位处按照相同间隔依次测量出试件的四根(编号为1—4)曲线,利用SJ软件提取出试件的表面粗糙度曲线。图5为2 号试件的四根表面粗糙度曲线。
从图5中可以看出,粗糙度曲线上下波动较大,出现了不规则的重叠。这表明经过打磨后的试件表面凹凸不平,并存在较大的缺口凹陷,形成了较为粗糙的表面形貌。
3.2 插值法建立曲面模型
插值是一种函数逼近的基本方法,利用插值方法可对有限数据进行函数近似值估算,实现了在原始离散采样点的基础上继续补插连续函数,并保证数据在所使用的范围内。常用的插值方法主要有线性插值、自然邻点插值。
本文提出的插值方法的基本原理是:首先以Excel格式保存曲线数据。把原本的四根曲线横坐标作为Z轴,考虑到粗糙度曲面为三维曲面,因此添加新的纵坐标Y轴。为避免Y轴间距过大出现表面过于粗糙的现象,使用线性插值法进行建模。先选择原本的任意两条相邻曲线,它们对应的Y值是n、n+1,在这两条曲线中间重新插入100 个Y值。接着给每一个新增加的Y值插值对应的X-Z值曲线,则可通过曲线数据将三维曲面插值出来。假设X为新曲线的X值,Z为新曲线的Z值,对应的Y为Y值,则计算公式如下:
Z=(linen+1(X)-linen(X))×(Y-n)+linen(X) (1)
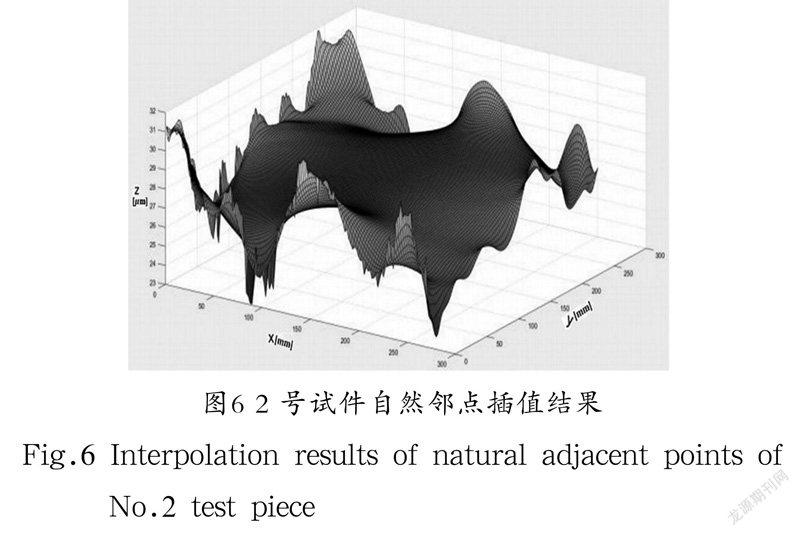
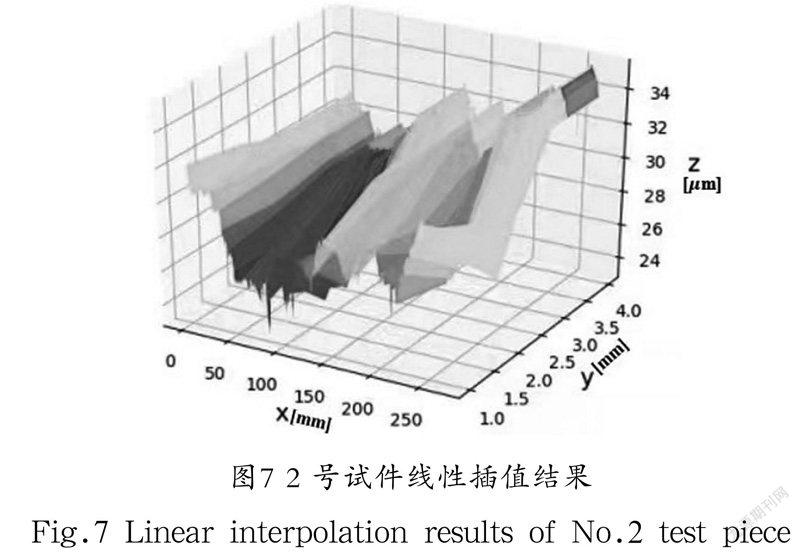
本文基于曲线选用自然邻点插值法和线性插值法得到的2 号试件三维粗糙度曲面模型如图6和图7所示。
从图6中可以看出,使用自然邻点插值法会丢失大量重要的表面形貌数据,且插值结果的中间部位过于光滑,表面粗糙度的相关信息没有体现,这与实际情况相差太大,故不采用该方法。因此,通过线性插值法进行三维曲面模型的计算。
3.3 三维实体模型的建立
为了后续仿真分析的需要,将插值法得到的三维曲面模型转化为实体模型。本文在Solidworks软件中创建三维实体模型。使用“通过XYZ点的曲线”命令插入得到曲面三维坐标X值、Y值、Z值,获得曲面模型;再通过拉伸、切除命令完成表面粗糙度实体模型的建立。图8为创建的带有表面粗糙度的2 号试件模型。
3.4 有限元模型的建立与仿真
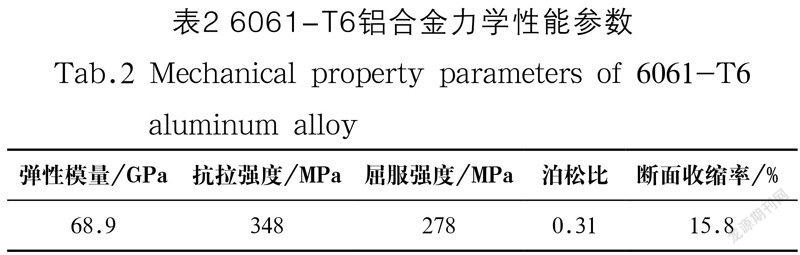
将得到的表面粗糙度实体模型导入Abaqus有限元软件中进行受力分析。本文使用的材料是6061-T6铝合金,通过静态拉伸试验获得其基本力学参数,具体数据如表2所示。
由于断裂区域仅发生在试件中间部分,因此对试件中间区域进行局部网格细化,其他区域网格可以适当放大,以提高计算效率与正确性。对模型拉伸一端添加均布载荷P=103.3MPa,另一端施加对称约束。模型的网格划分与应力云图如图9所示。
3.5 疲劳仿真寿命分析
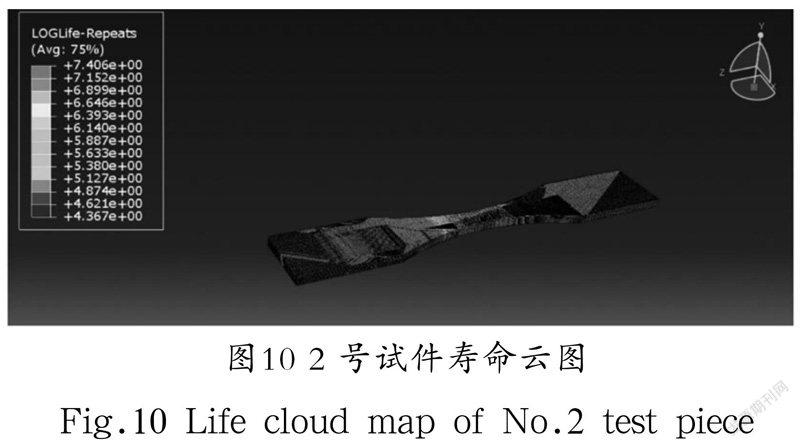
采用FE-SAFE疲劳分析软件对表面粗糙度试件进行寿命分析。在FE-SAFE软件中输入材料的基本参数,利用Seeger算法获取R=0.1的S-N曲线。设置载荷信息与约束条件后将疲劳计算结果导入Abaqus中進行后处理。为了与实际工况相符,使用Goodman平均应力修正法进行分析,得到的表面粗糙度试件寿命云图如图10所示。
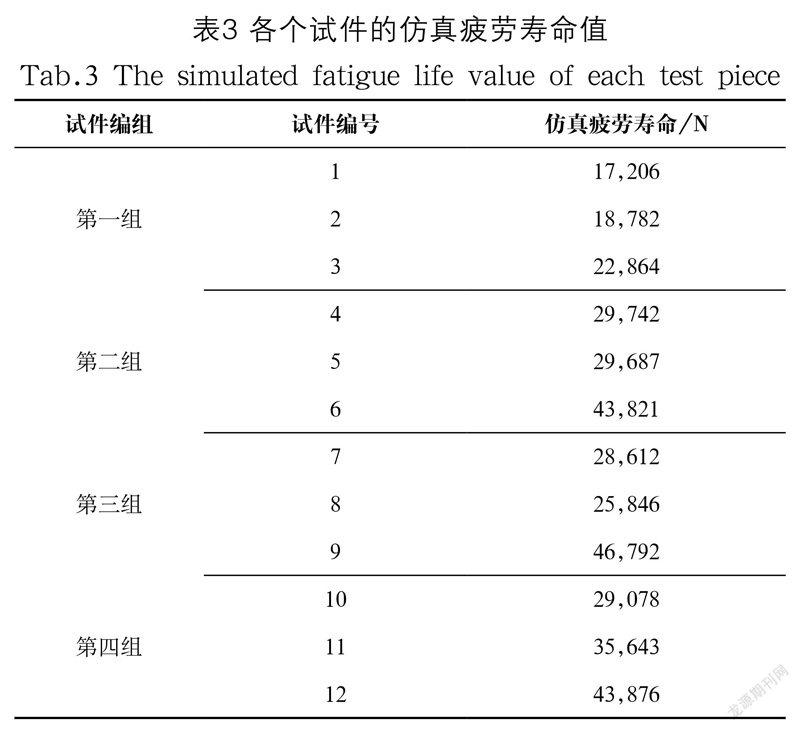
从图10中可以看出,模型中间部分寿命最小。这是由于此处横截面积最小,受到的应力最大。同时粗糙度增大,使得试件所受应力加剧,疲劳寿命减小。表3展示了粗糙度试件的仿真疲劳寿命值。
3.6 模型结果验证
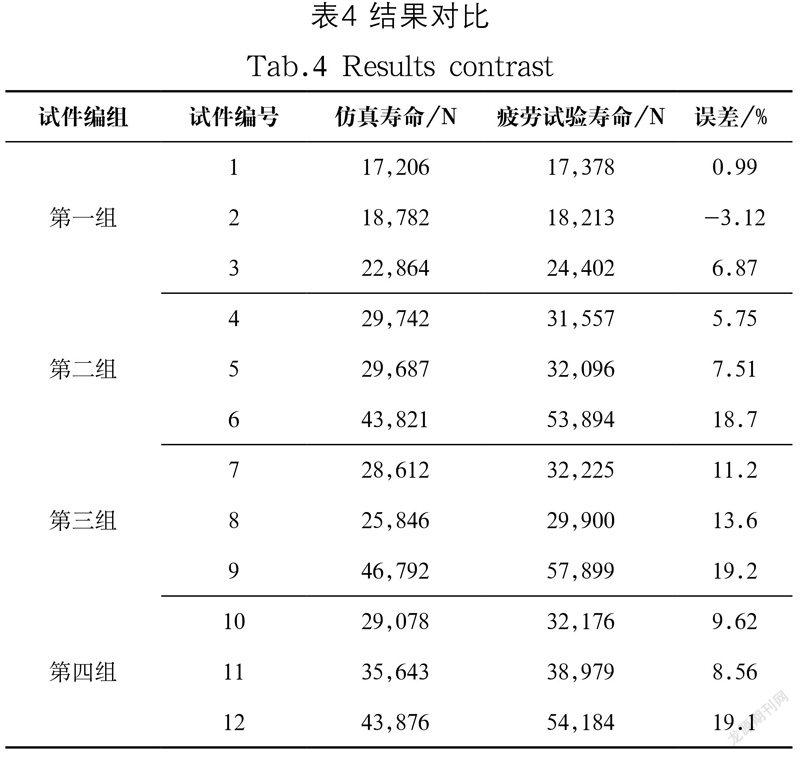
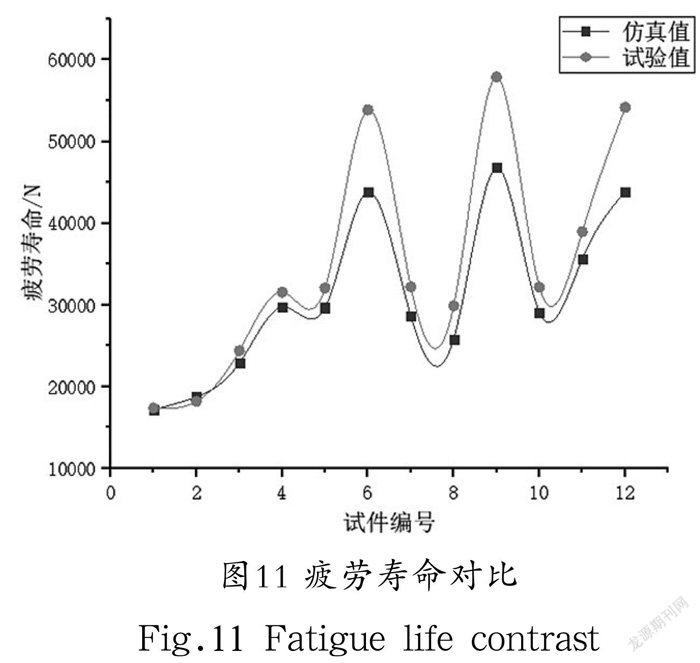
为了验证插值法构造的粗糙度模型,将仿真和试验结果进行对比分析,证实了该模型的有效性。对比结果如表4和图11所示。
由上述试验与仿真的对比分析可以看出,随着试件粗糙度值的降低,疲劳寿命逐步提高,两者寿命的变化趋势基本一致,且数值吻合较好,最大误差为19.2%,从而验证了使用插值法重构粗糙度模型的有效性与正确性。
4 表面粗糙度对疲劳寿命的影响(The effect of surface roughness on fatigue life)
4.1 建立表面粗糙度参数的有限元模型
由于提取试件表面粗糙度曲线需要借助特定的软件,通过有限的试验获得疲劳寿命费时费力[11]。结合现有的设备选择表面轮廓算术平均偏差Ra、轮廓最大高度Ry、微观不平度十点高度Rz作为粗糙度参数,按照蒙特卡洛法得到表面粗糙度曲线[12-14]。
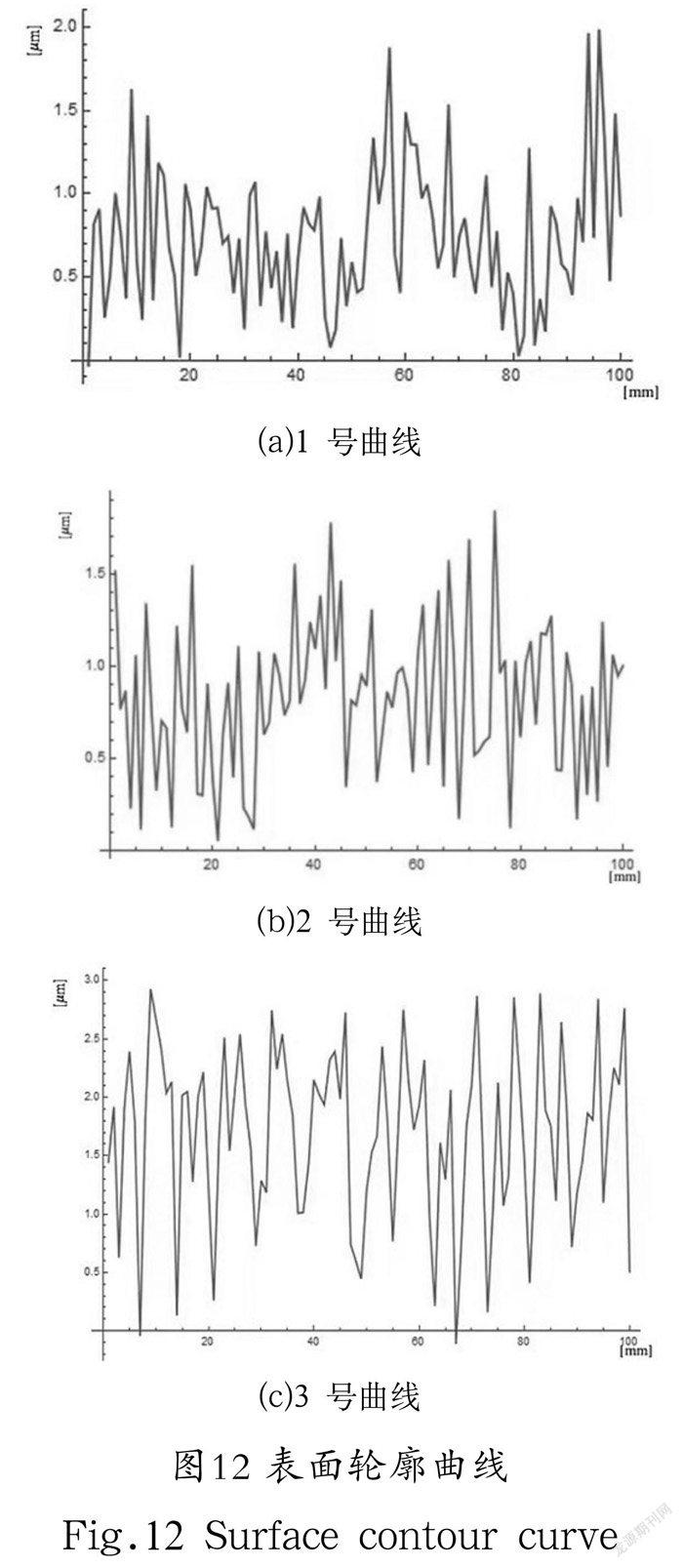
首先设定一个上限和相对误差,根据粗糙度仪测得每个试件的Ra、Ry、Rz数据,选择ц=Ra、σ=0.2Ry的随机正态分布函数参数来表示置信区间。通过Mathematica软件的RandomVariate函数调用ц和σ作为正态分布参数,产生10000×100 个随机数。通过将计算得到的随机数组Ra、Ry、Rz值与真实值进行比较,求出相对误差值的和,最后选取相对误差值最小的数据作为目标数组,并绘制表面粗糙度曲线。图12展示了粗糙度参数为Ra=1.187、Rz=4.752、Ry=2.640的三根表面粗糙度曲线。
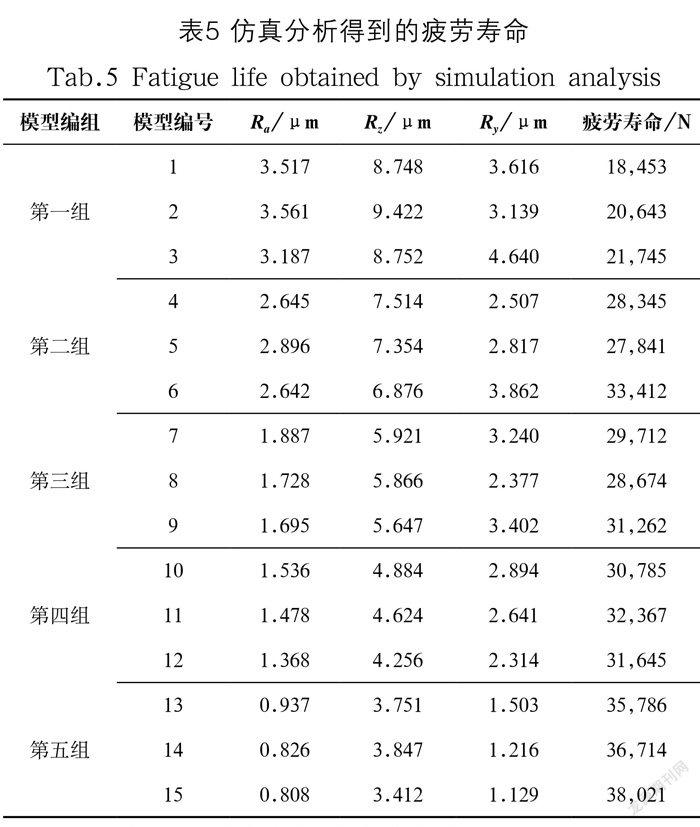
使用上文提出的插值法,对15 组粗糙度试件进行模型重构与寿命仿真,其结果如表5所示。
4.2 基于表面粗糙度参数的疲劳寿命预测
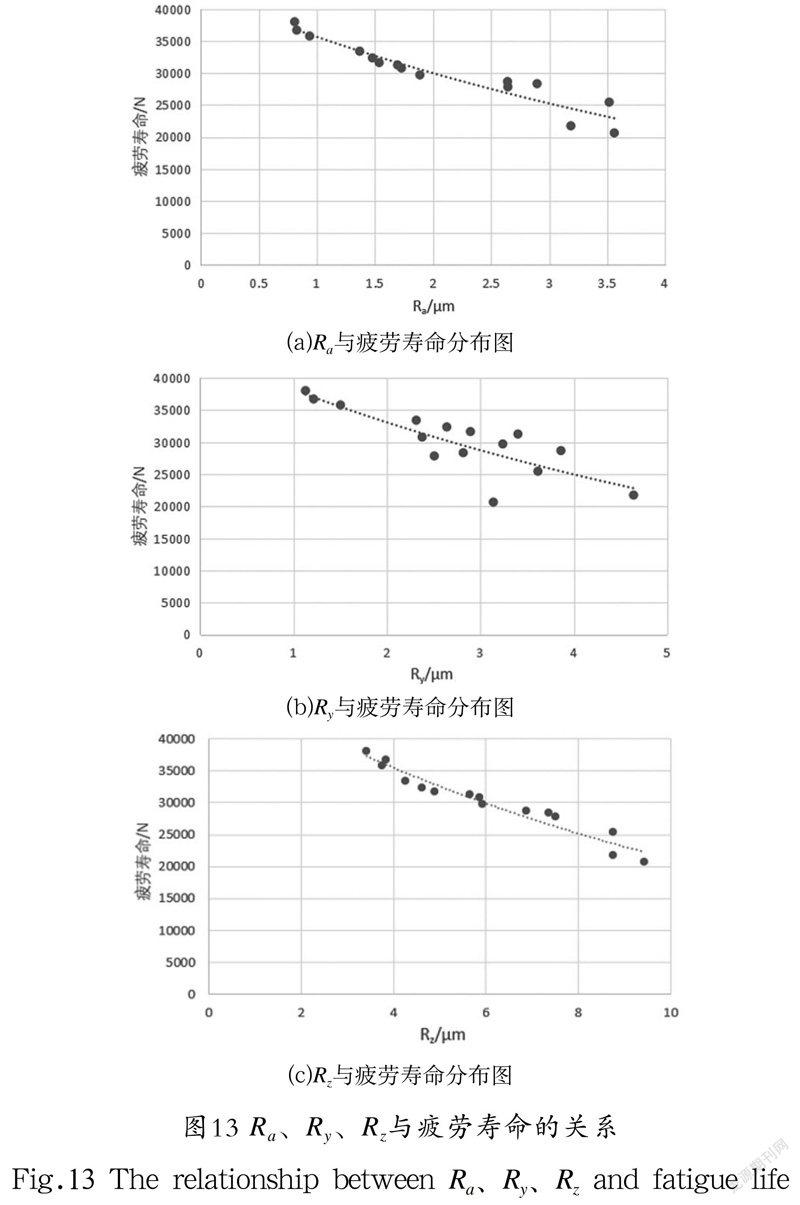
由表5可得粗糙度参数Ra、Ry、Rz与疲劳寿命的关系,如图13所示。
从图13(a)可以看出,随着Ra值的增加,疲劳寿命有明显的幂函数下降趋势。因此建立幂函数模型来描述Ra与疲劳寿命N的关系,如公式(2)所示:
基于上述公式,通过粗糙度参数可计算得到疲劳寿命。
5 结论(Conclusion)
本文基于插值法重构的表面粗糙度模型,研究了不同粗糙度参数对铝合金材料疲劳寿命的影响。同时使用有限元的方法计算出试件的疲劳寿命,建立了粗糙度参数与疲劳寿命之间的函数关系,并最终实现了寿命预测。本文的主要结论如下:
(1)提出了一种基于表面粗糙度曲线的插值法重构真实试件表面形貌的方法。将该方法得到的结果与试验结果对比,发现两者最大误差为19.2%,证明了该方法的正确性。同时研究表明,降低零部件表面粗糙度值可有效提高零部件的疲劳寿命。
(2)从影响疲劳性能和抗裂性能的角度选择Ra、Ry、Rz作为主要粗糙度参数,分析了其与疲劳寿命的关系。结果表明,粗糙度参数与疲劳寿命之间存在幂函数关系,可开展疲劳寿命预测。
参考文献(References)
[1] 曾泉人,刘更,刘岚.机械加工零件表面完整性表征模型研究[J].中国机械工程,2010,21(24):2995-2999.
[2] 蔡其刚.铝合金在汽车车体上的应用现状及发展趋势探讨[J].广西轻工业,2009(01):28-29.
[3] SURARATCHA M, LIMIDO J, MABRU C, et al. Modelling the influence of machined surface roughness on the fatigue life of aluminium alloy[J]. International Journal of Fatigue, 2008, 30(12):2119-2126.
[4] 趙丙峰,谢里阳,李冲,等.构件不同部位粗糙度对疲劳性能影响差异分析[J].机械工程学报,2020,56(02):43-55.
[5] 杨国庆,熊美华,洪军,等.3D粗糙表面的数字化表征与接触特性分析[J].西安交通大学学报,2012,46(11):58-63.
[6] 唐兵.一种电子装备表面粗糙度的重构方法研究[D].西安:西安电子科技大学,2015.
[7] 梅倩倩.基于高斯滤波技术的表面粗糙度的提取[D].洛阳:河南科技大学,2015.
[8] 郑清春,王乃鑫,朱培浩,等.铝合金薄板自冲铆接疲劳寿命仿真与分析[J].锻压技术,2020,45(09):93-98.
[9] 周鹏.碳纤维复合材料工件切削表面粗糙度测量与评定方法研究[D].大连:大连理工大学,2011.
[10] 袁伟.基于MATLAB和Solidworks的弧面凸轮设计及3D建模[J].精密制造与自动化,2014(02):25-27.
[11] JAVADI H, JOMAA W, TEXIER D, et al. Surface roughness effects on the fatigue behavior of as-machined inconel718[J]. Solid State Phenomena, 2016, 258:306-309.
[12] VAYSSETTE B, SAINTIER N, BRUGGER C, et al. Surface roughness of Ti-6Al-4V parts obtained by SLM and EBM: Effect on the high cycle fatigue life[J]. Procedia Engineering, 2018, 213:89-97.
[13] 郑修麟.循环局部应力-应变与疲劳裂纹起始寿命[J].固体力学学报,1984(02):175-184.
[14] 罗学昆,吴小燕,王科昌,等.表面完整性对FGH95合金高温疲劳性能的影响[J].航空材料学报,2020,40(02):53-60.
作者简介:
杨永康(1997-),男,硕士生.研究领域:汽车零部件疲劳损伤及轻量化.
杨亚莉(1982-),女,博士,副教授.研究领域:汽车零部件疲劳损伤及金属断裂机理.
付仁杰(1996-),男,硕士生.研究领域:汽车零部件疲劳损伤及轻量化.

