分数阶微分方程多点边值问题正解的存在性
赵 微,李 立,李 娜,王 冲,郭 锐,白旭亚
(1.大庆师范学院 数学科学学院,黑龙江 大庆 163712;2.黑龙江职业技术学院,黑龙江 哈尔滨 163300)
分数阶微分方程是数学研究领域中的一个热门课题。学者们已讨论了不同类型的分数阶微分方程边值问题解的相关问题。(1)参见江卫华、董倩:《Conformable分数阶微分方程三点共振边值问题解的存在性》,《吉林大学学报》(理学版)2021年4期等。由于分数阶微分方程能广泛地应用于流体力学、非牛顿力学等领域,所以对分数阶微分方程及其边值问题进行深入探讨,有着重要的理论及实际意义。
文中主要考虑如下分数阶微分方程多点边值问题
(1)
的正解存在性,其中ηi∈(0,1),0<η1<η2<…<ηm-2<1,βi∈[0,+∞)。
首先构造出上述问题的格林函数,推导其相关的性质;其次,通过计算相应锥上的凸泛函不动点指数,得到了分数阶微分方程多点边值问题(1)至少存在一个正解的结论。对于分数阶微分方程边值问题正解的研究,多数运用锥拉伸与压缩定理、Leggett-Williams不动点定理、上下解、Banach压缩映射原理等方法,文中所用的方法不同于以往文献。
1 准备工作
下面先介绍一些文中所需要用到的定义和引理。
定义1 函数y:(0,+∞)→R的ν>0阶Riemann-Liouville积分定义如下
其中右边是在(0,+∞)上逐点定义的。(2)参见赵微:《一类分数阶微分方程m点边值问题的正解》,《湖南师范大学自然科学学报》2018年第3期。
定义2 函数y:(0,+∞)→R的ν>0阶Riemann-Liouville微分定义如下为
其中N=[α]+1,右边是在(0,+∞)上逐点定义的。(3)参见赵微:《一类分数阶微分方程m点边值问题的正解》。
引理1 假设u∈C(0,1)∩L[0,1]有ν>0阶导数属于C(0,1)∩L[0,1],则
Ci∈R,i=1,2,…,N,其中N大于或等于ν的最小整数。
其次进行下述假设:

(H3)f:[0,+∞)→[0,+∞)连续。
引理2 给定g∈C[0,1],边值问题
(1)
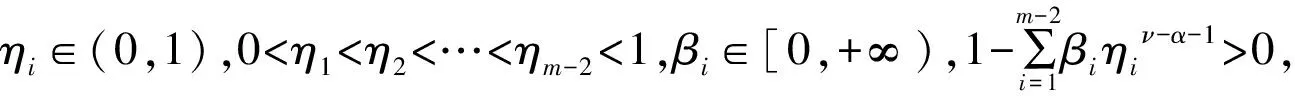

其中
证明 应用引理1,将上述微分方程转化为等价的积分方程
由u(0)=u′(0)=u″(0)=…=u(n-2)(0)=0,得出C2=C3=…-Cn=0。
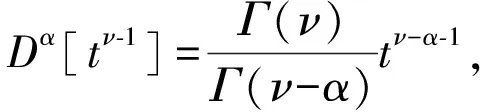
整理计算得到

于是



引理3p(s)满足:
(i)p(s)在[0,1]上单调不减且恒正;
(ii)存在M≥m≥0使得任意s∈[0,1],有ms+p(0)≤p(s)≤Ms+p(s),其中
证明 (i)因为
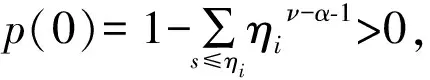

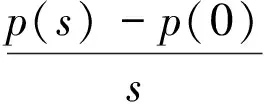
引理4G(t,s)满足下面不等式:
证明 (i)当0 当0 (ii)当0 当0 令 (2) 引理5 若满足(H1)—(H3),那么由(2)定义的算子A∶P1→P1是全连续的。 证明 由引理4及算子A的定义知, 于是 所以A∶P1→P1,且A(P1)⊂P1。再由Arzela-Ascoli定理知,算子A∶P1→P1全连续。 定义3 如果锥P上的泛函ρ∶P→R,对于∀x,y∈P,t∈[0,1]满足 ρ(tx+(1-t)y)≤tρ(x)+(1-t)ρ(y), 则称ρ是锥P上的凸泛函。(4)参见赵微:《奇异四阶微分方程m点边值问题正解的存在性》,《西南师范大学学报》(自然科学版)2020年第10期。 设 显而易见有h0≥hτ>0。 定理1 若(H1)—(H3) 满足,且有0 (1)f(u(s))≤h0-1u,∀u≤bl-1hτ-1; (2)f(u(s))≥hτ-1u,∀ahτ-1l≤u≤ahτ-1l-1。 则上述分数微分方程边值问题(1)至少存在一个正解。 对于∀u∈{θ}, 假设A在P1∩∂Ω1上没有不动点,则有i(A,P1∩Ω1,P1)=1。(5)参见赵微:《奇异四阶微分方程m点边值问题正解的存在性》,《西南师范大学学报》(自然科学版)2020年第10期。 设Ω2={u∈C[0,1]|ρ1(u) 如果u∈P1∩∂Ω2,则ρ2(u)=a且u≤al-1hτ-1,由于 所以 假设A在P1∩∂Ω2上没有不动点,可得i(A,P1∩∂Ω2,P1)=0。 定理2 若(H1)—(H3)满足,且有0 (2)f(u(s))≥hτ-1u,∀blhτ-1l≤u≤bl-1hτ-1; (3)f(u(s))≤ah0-1u,∀u≤al-1, 则分数阶微分方程边值问题(1)至少存在一个正解。 证明 因为 bl-1hτ-1≤al2hτ2h0-1l-1hτ-1=alhτh0-1 对于∀u≤bl-1hτ-1,有 hτ-1u≤hτ-1bl-1hτ-1=(hτ-1)2al2hτ2h0-1l-1=alh0-1 令 于是,ρi∶P1→[0,+∞)是一致连续凸泛函,且ρi(θ)=0(i=1,2)。又∀u∈P1{θ},有 令Ω1={u∈C[0,1]|ρ2(u) ρ1(u)≤u≤bl-1hτ-1 假设A在P1∩∂Ω1和P1∩∂Ω2上没有不动点, 如果u∈P1∩∂Ω1,则b=ρ2(u)≤uhτ,且进一步则有 所以i(A,P1∩Ω1,P1)=0; 如果u∈P1∩∂Ω2,则 i(A,P1∩Ω2,P1)=1,(7)参见赵微:《奇异四阶微分方程m点边值问题正解的存在性》,《西南师范大学学报》(自然科学版)2020年第10期。 综上可得:i(A,P1∩(Ω2Ω1),P1)=1。 于是对于上述分数阶微分方程多点边值问题(1)而言,至少有一个正解。 文中通过构造分数阶微分方程多点边值问题的格林函数,推导格林函数的相应性质,通过计算相应锥上的凸泛函不动点指数,得到了一类分数阶微分方程的多点边值问题(1)至少有一个正解存在的两个充分条件,所用方法不同于以往文献。
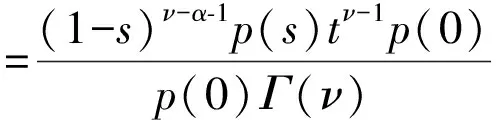

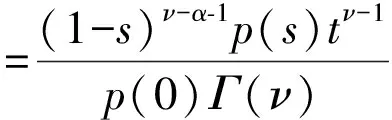



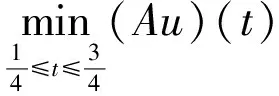
2 定理
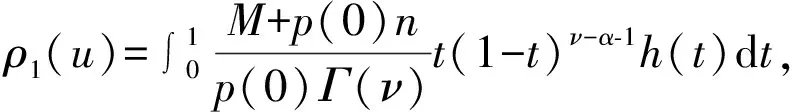


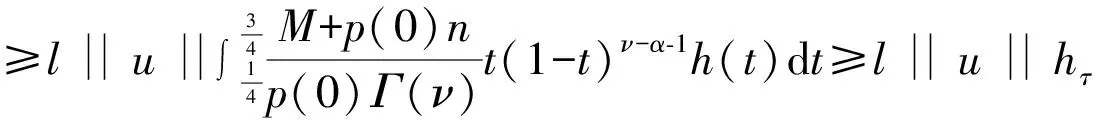

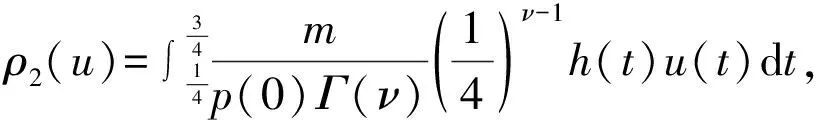

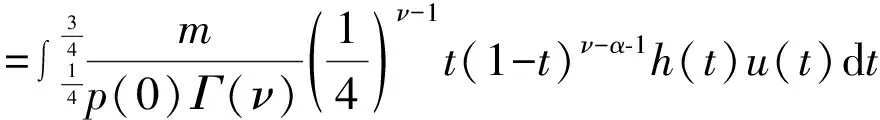
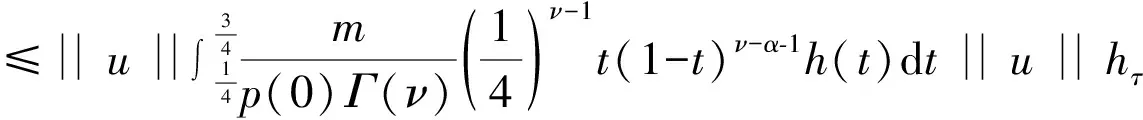

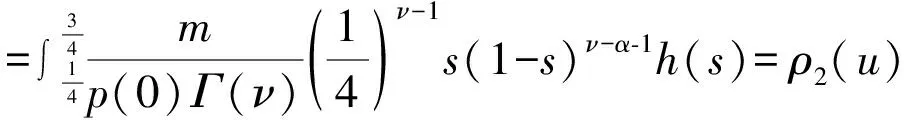
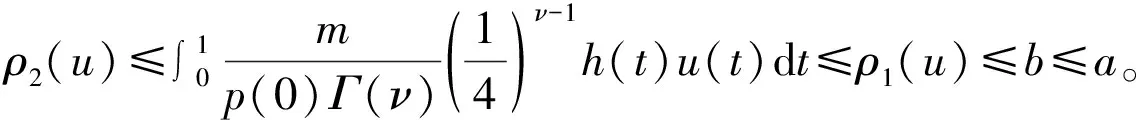
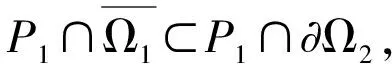
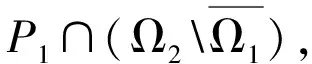



3 结 语

