基于Delaunay三角网法的土石方量计算精度探讨
候汉霜
(深圳市长勘勘察设计有限公司,广东 深圳 518003)
1 引 言
土石方量的计算结果关系到工程项目的各方利益,目前我们常采用的土石方量计算方法有断面法、方格网法、等高线法、平均高程法和DTM(数字地面模型)法等。其中,每一种计算方法都有其适用条件和适用范围,断面法计算土石方量适合在线状地形使用,比如道路、河流渠道等;方格网法在比较平坦的地区或者地形起伏不大的场地上更经济实用;而在地形起伏较大、精度要求高的区域则需使用DTM法来计算土石方量较为合理。DTM法由于考虑了地形特征(采用不规则三角网TIN法建模),并以原始测量采集的数据作结点的三角形为最小计算单元,从理论上来说是计算土石方量最为精确的方法。而通过建立Delaunay三角网保证得到的是最优的TIN模型,一般情况下是计算土石方量的最佳选择。目前,主流的Delaunay三角网生成算法有三种:分割合并法、逐点插入法和三角网生长法。本文采用三角网生长法编写基于Delaunay三角网的土石方计算程序,探究Delaunay三角网法土石方计算的方案与南方CASS软件中传统三角网法方案对比在土方量计算精度的偏差。
2 基于Delaunay三角网法的土石方量计算方法
土石方量的计算是通过地形表面模型和设计表面模型进行叠加,求出叠加后所夹空间区域的体积从而得到土石方量。这里需要分别建立地形表面TIN模型和设计表面TIN模型。
2.1 地形表面TIN模型的构建
要建立地形表面TIN模型必须先确定TIN模型中三角形的形成法则,即三角剖分准则。常用的三角形剖分准则为以下6种:①张角最大准则:一点到基线边的张角是最大的;②空外接圆准则:就是TIN中过每个三角形的外接圆均不包含点集除了该三角形的顶点之外的任何其他点;③最大最小角准则:每两相邻三角形所形成的凸四边形中,这两个三角形的最小内角一定大于交换该凸四边形对角线后新形成的两三角形的最小内角;④最短距离和准则:即一点到基线边两个端点的距离之和是最小的;⑤对角线准则:若是两三角形组成凸四边形的两条对角线之比超过限定阈值时,则需要对三角形进行优化;⑥面积比准则:就是三角形的面积与周长平方之比最小(或者三角形内切圆的面积与三角形的面积之比最小)。在理论上已经证明了张角最大准则、空外接圆准则和最大最小角准则是等价的,但其他的则不是。其中对角线准则受主观因素影响,已经很少用到。
通常将在空外接圆准则、最大最小角准则下进行的三角剖分称为Delaunay三角剖分(简称DT)。并且空外接圆准则与最小角最大准则是Delaunay三角网的两个基本性质。实际上,任何三角剖分准则下得到的TIN,只要利用LOP法则(局部优化过程,Local optimal procedure,Lawson于1977年提出)来进行优化处理,都能得到一个唯一的DT三角网。
2.2 设计表面TIN模型的建立
在各种土方工程中,设计表面可以图形的方式给出,也可以数学函数的形式给出,如场地平整平面,整个区域可有不同的表达式,例如道路设计表面中的左右边坡、路面等。
若设计表面以数学表达式给出,则地形表面TIN模型和设计表面模型TIN在平面位置上具有相同的三角网形,而在同一平面位置上地面模型与设计模型的高程值不同。但是设计表面TIN模型的高程可由模型的三角形顶点坐标代入到设计表面函数计算得到。设地形表面TIN模型三角形顶点P坐标为(xp,yp),设计表面函数为HD=g(x,y),则P点的设计高程为Hd(P)=g(xp,yp)。根据设计表面函数求出每个地形表面三角形顶点所对应的设计高程,则可建立相应的设计表面TIN模型。
若设计表面以图件形式或散点形式给出,则可先对设计表面建立TIN。但由于地形表面模型和设计表面模型具有不同的三角网形结构。这时要进行数据加密处理,即把设计表面中的点内插到地形表面上,并求出设计表面散点对应的地面高程;同时,将地形表面上的点内插到设计表面中,并求出地形点对应的设计高程。另外,不同的TIN模型上,三角形边相交处的坐标和高程也相应求出。这样就建立了具有相同结构的两个TIN模型。
2.3 土石方量的计算
得到地形表面TIN模型和设计表面模型TIN后,通过叠加产生地形表面与设计表面高程差异,从而在三维空间上形成不同结构的棱柱体。土石方量计算其实就是计算三角棱的体积,通过计算三角网中每个三棱锥柱的填挖方量,再求和得到整个三角网的总填挖土石方量。
根据三角形三个顶点地形高程和设计高程情况,每个三角形区域分为全填全挖或有填有挖两种情况考虑。当三角形三个顶点的高程都大于(或小于)设计高程。如图1(a)所示。
(1)
式(1)中:S为三角形投影到水平面的面积;H1,H2,H3分别为三角形三个顶点与设计面的高差(取绝对值)。
当三角形三个顶点的地形高程值既有大于也有小于设计高程。这时设计面将三角形分成两部分,一部分为底面是三角形的锥体,另一部分是底面为四边形的楔体。如图1(b)所示。锥体部分和楔体部分的体积计算公式分别为:
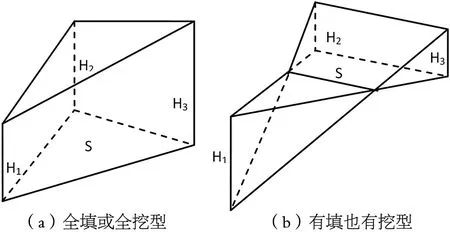
图1 三角棱柱的体积计算
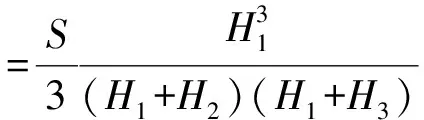
(2)
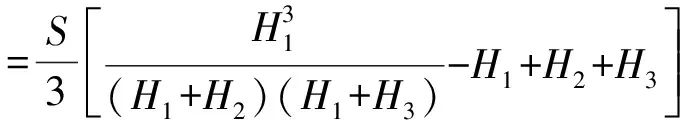
(3)
式(2)和(3)中:S为三角形投影到水平面的面积;H1,H2,H3为三角形三个顶点与设计面的高差(取绝对值),其中H1恒指锥体顶点与设计面的高差(取绝对值)。另外,有填方也有挖方在实际计算过程中主要分为6种情况考虑,即:①H1<0,H2>0,H3>0;②H1>0,H2<0,H3>0;③H1>0,H2>0,H3<0;④H1>0,H2<0,H3<0;⑤H1<0,H2>0,H3<0;⑥H1<0,H2<0,H3>0。
3 程序实现与实验分析
3.1 程序实现
为了分析Delaunay三角网法计算土石方的效果,笔者采用三角网生长算法编写基于Delaunay三角网法计算土石方的程序。考虑到便于对所剖分的离散点集和形成的三角形进行管理,程序设计3个单向链表类。它们分别是:①点表类(CPointList),用于管理的离散点集。参数有点名(PointName)、点号(indexP)、X坐标(x)、Y坐标(y)和Z坐标(z),还有该点是否为封闭点(closePoint)以及一点所在的圆环号(RingNum)。②边表类(CEdgeList),用于管理三角剖分后生成的每一条边。类的参数有边号(indexE)、起始点(startPt)、终止点(endPt)和该边的已被几个三角形共用(useCount)。其中起始点(startPt)和终止点(endPt)均属于点表类(CPointList)。③三角形表类(CTriList),用于管理三角剖分后生成的每一个三角形。类的参数有三角形号(indexT)、三角形的L0边(L0)、三角形的L1边(L1)和三角形的L2边(L2)。其中三角形的L0边(L0)、三角形的L1边(L1)和三角形的L2边(L2)均属于边表类(CEdgeList)。其程序实现过程如下:
(1)创建初始三角形
在数据集中找到距几何中心最近的点A,再找到距A点最近的点B,由点A、B组成第一条基线AB。然后对数据集进行搜索,找到与AB边有最大夹角的点C,将A、B、C三点按逆时针链接形成初始三角形,并且给边AB(L0边)、BC(L1边)、CA(L2边)的扩展次数(useCount)赋为1。并规定以后每生成一个三角形,都按照逆时针方向链接三个顶点。
(2)扩展边以形成整个区域的无约束Delaunay三角网
有了初始三角形,后面的工作就是开始循环逐步扩展生成三角网,设从第triNum个三角形开始,分别对三角形triNum的三边L0、L1、L2做如下处理(以L0边为例):
①查找可用的顶点。要扩展生成下一个三角形,下一个点必定不是三角形triNum上的点,而且也不是与C点在同一侧。
②找出可用点中与边L0形成夹角最大的那个点。然后与L0两端点连接完成三角形的一次扩展,并给L0边的useCount值+1。
分别处理L1、L2边,并以此循环,直到三角形的个数不再增长,则完成整个数据域的无约束Delaunay三角网生成。
(3)将生成的点表、边表、三角形表传递到绘图类、土方计算类中。
(4)绘图类中将每一条边绘制,连接成网。
(5)土方计算类中,对每个三角形进行计算,最后计算所有三角形的填挖方总和。这里主要有三种情况:仅有填方、仅有挖方和既有填方也有挖方。其中既有填方也有挖方又细分六种情况考虑。
3.2 土石方量计算结果比较分析
为了说明Delaunay三角网法土石方量计算本文方法精度,进行了仿真测试精度分析和实际测量精度分析。
(1)仿真测试精度分析
利用曲面函数构造模型进行测试(图2),首先对该函数进行积分计算(本处指定z=0,a=16,b=16,-50≤x≤50,-50≤y≤50)。因为这里指定a=b,所以该曲面是对称的,当|x|>|y|时z<0,即此时为填方,反之为挖方,且填挖方量相等。而|x|=|y|将区域分成4个部分,4个部分的计算结果绝对值相等:

图2 双曲抛物面示意图

V总=4×V=4×8138.021=32552.084

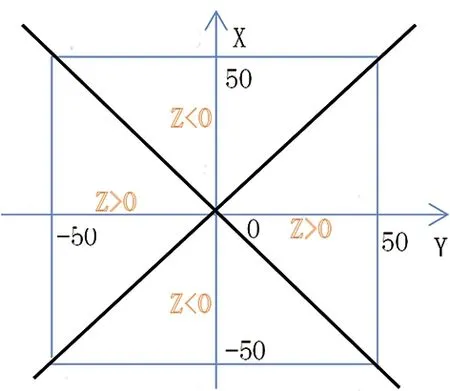
图3 划定双曲抛物面的测试区域范围

图4 函数的三维模型视图
在CASS7.0中生成三角网,并用DTM法计算土方,如图5所示。由图5可以看到,土石方总量=15632.268+15659.817=31292.085,与积分计算得到的结果(32552.084)有3.87%(1259.999方)的偏差。原因在于CASS7.0中三角网不是严格的Delaunay三角网,另外CASS生成的三角网的最外层边连成的多边形不是严格凸的。

图5 在CASS7.0中用DTM法计算1 009个点的土石方量
同样采用上面生成的1 009个点数据文件,在基于Delaunay三角网法程序中计算土石方量,如图6所示。由图6可以看到,这里土石方总量=16245.10+16274.10=32519.20,与积分计算得到的结果(32552.084)仅有0.10%(32.884方)的偏差。
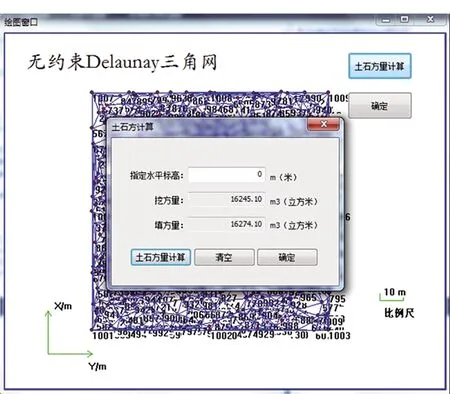
图6 Delaunay三角网算法下计算1009个点的土石方量
由于该函数对应的曲面是一个光滑曲面,参与计算的随机点越多,计算得到的土方量与积分结果越接近。为了证明点数与计算结果的精确性的关系,笔者还分别测试随机生成109个点、509个点和 2 009个点计算的土石方量作为比较的依据(图7):
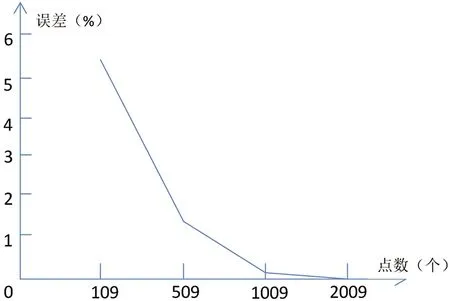
图7 测点数量与误差关系图
①109个随机点的测试结果为:土石方总量=15223.76+15623.66=30847.42,与积分计算得到的结果(32552.084)偏差5.24%(1704.664方)。
②509个随机点的测试结果为:土石方总量=16067.79+16060.36=32128.15,与积分计算得到的结果(32552.084)偏差1.30%(423.934方)。
③2 009个随机点的测试结果为:土石方总量=16265.75+16299.50=32565.25,与积分计算得到的结果(32552.084)仅偏差了0.04%(13.166方)。
通过这几次测试可以看到,同一个测试区域内,随着离散点数量的增加,计算得到的土石方量与积分得到的土石方量误差也越来越小。
(2)实际数据精度分析
为了说明基于Delaunay三角网法计算土石方量本文方法精度,笔者外业采用测绘仪器在野外选取一片地形稍有起伏的区域实地采集了21个点位坐标数据,如表1所示。
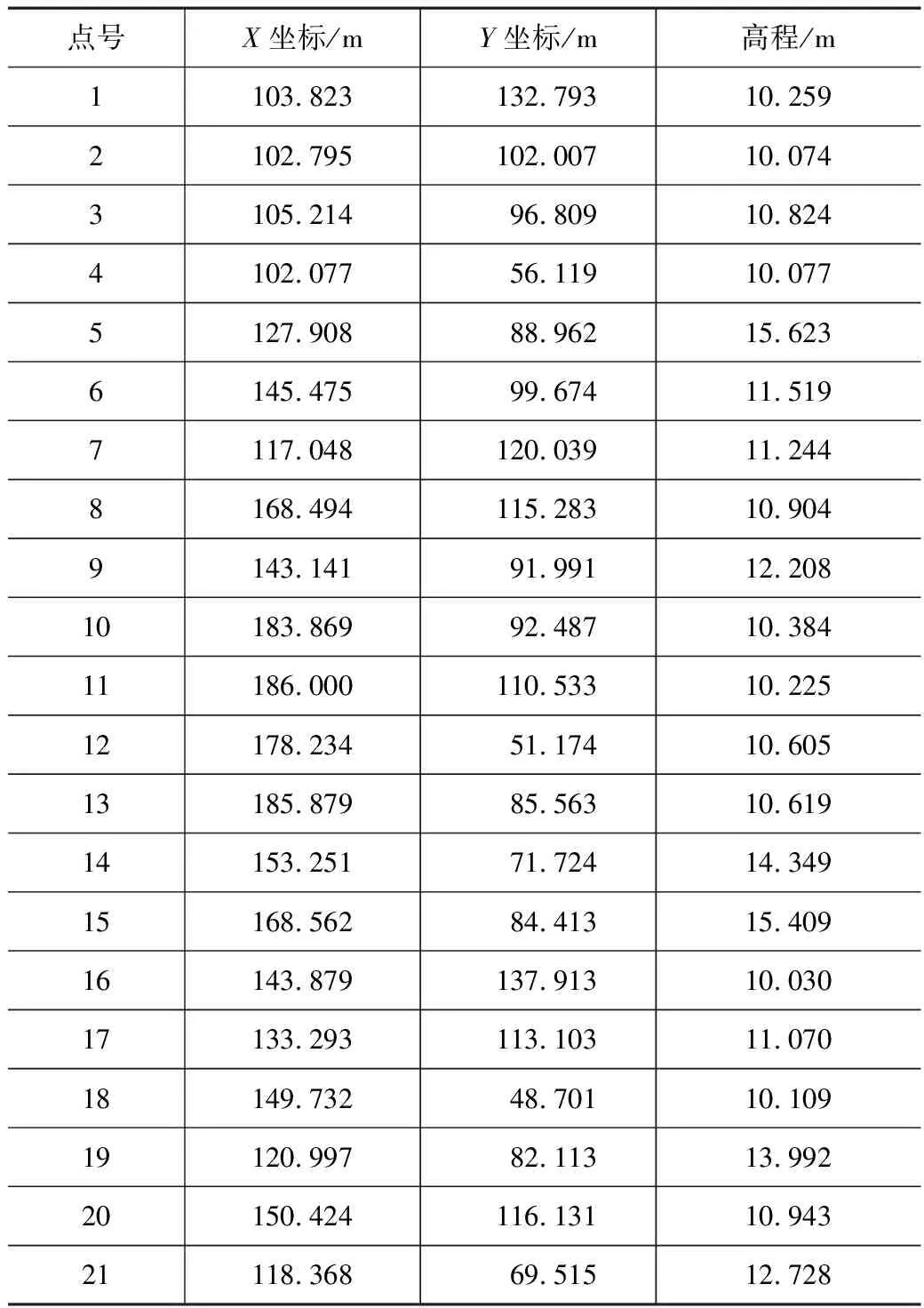
某区域实测数据 表1
内业利用南方CASS7.0生成DTM后计算的土石方量,其结果如图8所示,本文方法计算的土石方量如图9所示。
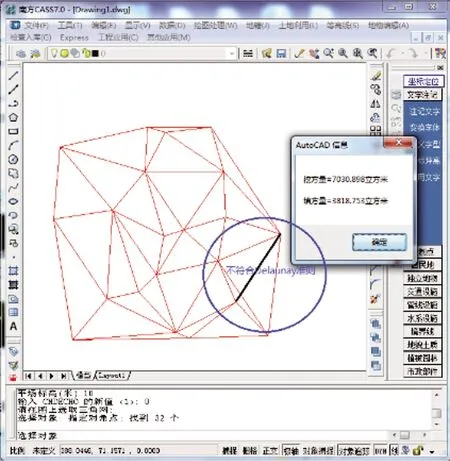
图8 CASS7.0的DTM法生成的三角网

图9 Delaunay三角网法生成的三角网
由图8、图9比较看出:基于Delaunay三角网法计算的挖方量与南方CASS7.0的不同。原因则是由于三角网的网形不相同,CASS7.0生成的三角网不符合Delaunay三角剖分准则(图8中画圈的四边形不满足空外接圆准则,需要交换对角线)。又根据前文(图5、图6对比)证明,本次实际数据测试基于Delaunay三角网法计算的精度更可靠。
4 结 语
本文通过数据测试表明,基于Delaunay三角网法计算得到的土石方量结果相比传统三角网计算的土石方量有较大精度上的提高,尤其在采样的数据点不是很密集的时候,表现更为明显。因此基于Delaunay三角网的TIN模型更接近实际地面模型,计算出的土石方量准确性更高。

