基于探索-利用权衡优化的Q学习路径规划

彭云建，梁 进

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

0 引 言

随着人工智能的发展，能自主移动的智能体机器人在工业、军事以及医疗领域得到广泛使用[1]，路径规划要求智能体避开障碍物，找到从出发点到目标点的最佳或次优路径[2]，是移动智能体被广泛使用和发挥价值的基础。其中未知环境下的路径规划是研究的难点和热点，目前主要的方法有人工势场法[3]、神经网络、遗传算法、粒子群等智能算法[4]。

在利用强化学习解决未知情况下的路径规划方面，M.C. Su等人提出在路径规划的理论中增加强化学习方法[5]。沈晶等人提出基于分层强化学习的路径规划的方法[6]。Y. Song 等人提出一种有效的移动机器人Q学习方法[7]。然而，在利用强化学习解决路径规划时，都会遇到强化学习本身固有的问题，即探索-利用问题[8]。为了解决探索-利用问题，目前提出的方法有ε贪婪方法和对其改进的ε-first方法[9]、ε-decreasing方法[10]，还有梯度算法[11]、value difference based exploration(VDBE)方法[12]等，但各有优点和不足，仍然有优化的空间。

该文根据优化ε值的改变方式和利用动作价值来动态选择采取的动作的思想，提出了基于探索-利用权衡优化的Q学习路径规划方法，解决移动智能体在未知环境下的路径规划问题。

1 探索-利用权衡优化的Q学习算法

为了实现智能体在未知环境下的路径规划，基于探索-利用权衡优化的Q学习路径规划可以分为两个部分，一是利用强化学习中Q学习不需要事先知道环境，智能体依然能与未知环境的互动中学习的特点，通过获得足够的幕数学习经验，不断更新Q表的动作价值，进而不断更新优化路径规划策略，实现路径规划；二是利用提出的εDBE方法和AεBS，权衡强化学习中固有的探索-利用问题，提高未知环境下路径规划的快速性。

基于探索-利用权衡优化的Q学习路径规划如图1所示。提出改进探索-利用权衡问题的εDBE方法和AεBS方法，着重优化ε值的改变方式和利用Q表中的动作价值来动态选择采取的动作，通过智能体与环境互动产生每幕学习经验来影响Q表动作价值的评估，进而获得更优动作行为、更新获得更优路径规划策略。

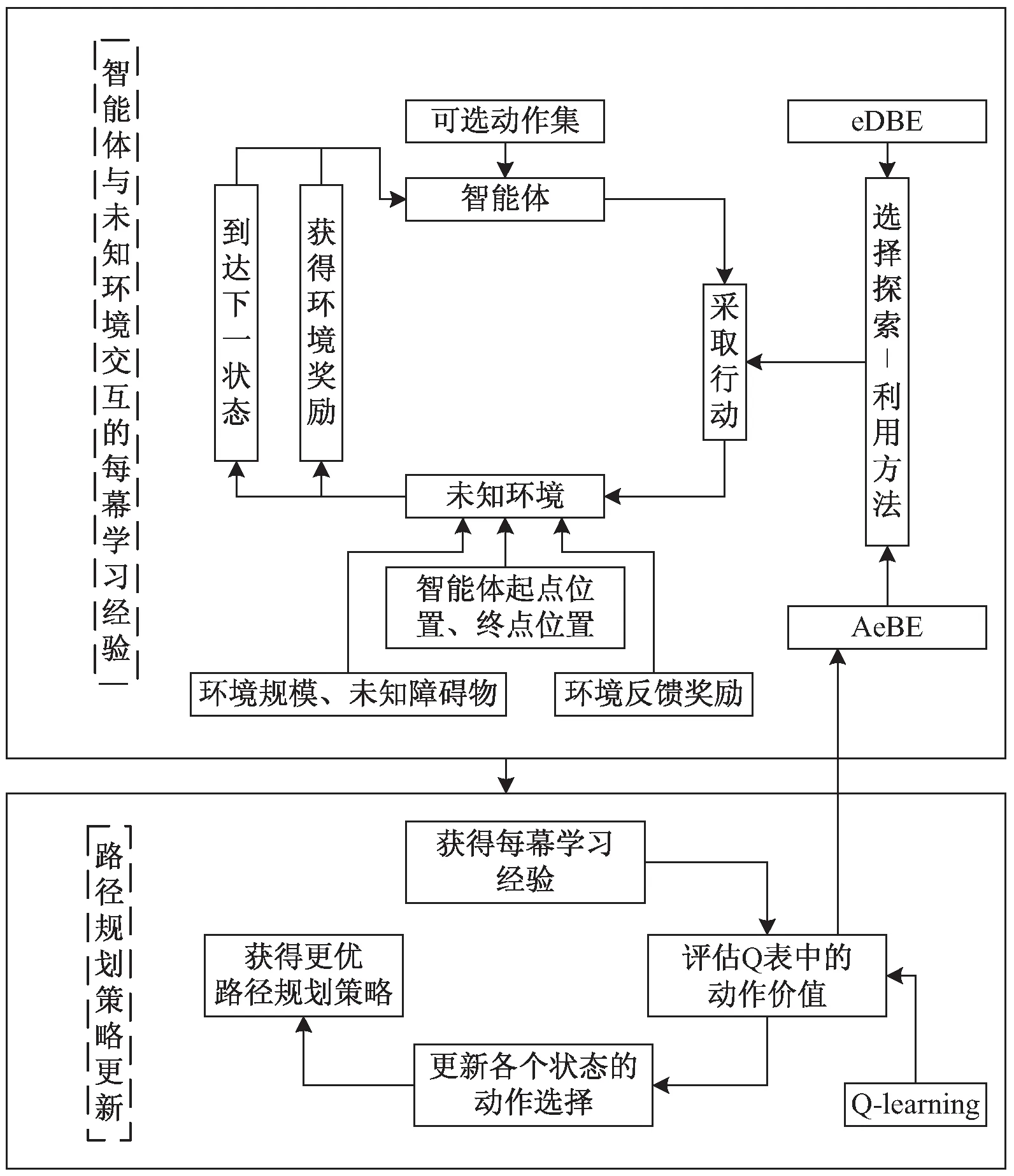
图1 探索-利用权衡优化的Q学习路径规划

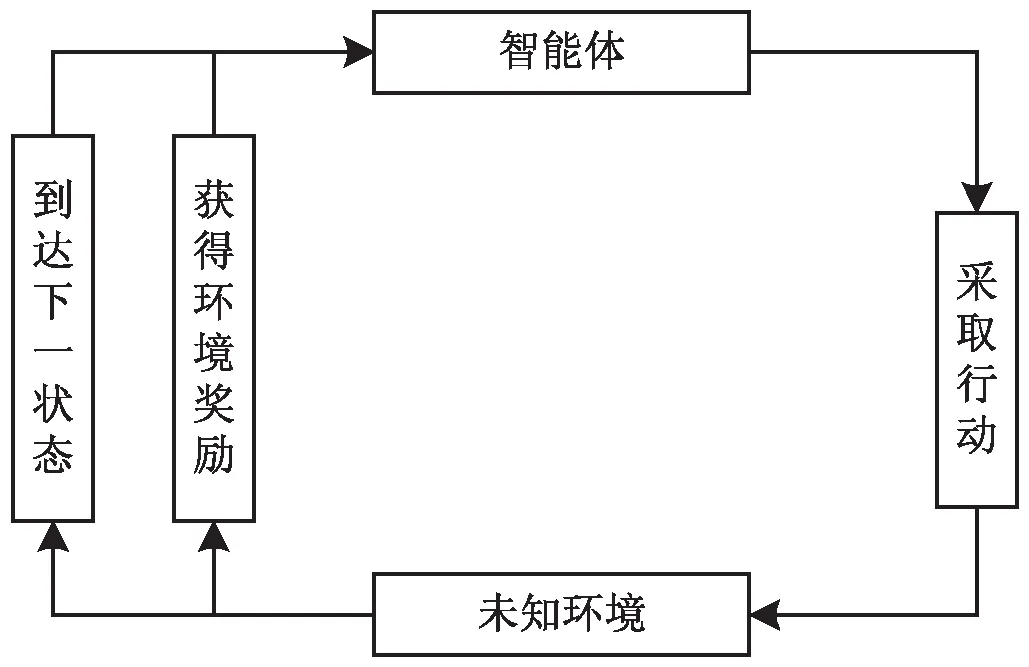
图2 智能体与环境交互图

智能体与环境交互如图2所示，每幕学习经验定义如下：在t时刻，智能体处于状态st，采取动作at，因此在t+1时刻，智能体获得来自环境的奖励rt+1，并在环境中发生了状态转移，到达了状态st+1。在智能体与环境的不断交互过程中可获得一个状态、行动、奖励的序列：s0，a0，r1，s1，a1，r2，s2，a2，r3，s3，…，sT,其中T是终止时刻，这样有终止状态的一个序列也称为一幕(episode)学习经验。

2 改进探索-利用权衡问题的εDBE方法和AεBS方法

2.1 权衡探索-利用问题的基本方法

为了解决强化学习固有的探索-利用问题，经典的Q学习算法中采用了ε-贪婪方法。之后有研究人员提出了改进ε-贪婪方法的ε-first方法、ε-decreasing方法，都是为了更好权衡探索-利用问题，提高Q学习算法解决问题的能力。

2.1.1ε-贪婪方法

ε-贪婪方法的思想是设定一个小的贪婪探索系数，0<ε≤1,在选择要采取哪个动作时，有ε的概率从所有可选的动作中随机选择，有1-ε的概率选择目前能获得最大回报的动作。可用式(1)表示：

(1)

其中，π(a|s)为在状态s下选择动作a的概率，m为状态s下动作集合A(s)中动作a的总个数,a∈A(s),a*为状态s下的最优动作。

2.1.2ε-first方法

ε-first方法[9]的思想是一开始将ε的值设为1，让智能体处于完全探索状态，一段训练幕数(episode)之后，将ε的值设为0，让智能体处于完全利用环境状态。可用式(2)表示：

(2)

其中，episode为幕数变量，preset_episo为预先设定的幕数值。

2.1.3ε-decreasing方法

改进的ε-decreasing方法[10]是ε-贪婪方法和ε-first方法的折中，思想是初始将ε设为一个较大的值，从训练幕数来看，ε随着训练幕数增加不断减少；从单幕的步数来看，ε随者步数增加而增大。可用式(3)表示：

(3)

其中，ε0为贪婪系数的初始设定值，episode为幕数变量，step为每幕的步数变量。

2.2 εDBE方法和AεBS方法

针对Q学习中固有的探索-利用问题，该文提出随幕数(episodes)平滑衰减ε-值的ε-decreasing based episodes(εDBE)方法，以及根据Q表中的状态动作值判断到达状态的陌生/熟悉程度、做出探索或利用选择的adaptiveεbased state (AεBS)方法。

2.2.1εDBE方法

随幕数(episodes)平滑衰减ε值的εDBE方法结合了ε-decreasing方法和ε-贪婪方法的特点，即将初始ε设为一个较小的值，从训练幕数的角度来看，随着训练幕数增加而不断衰减；从单幕的步数角度来看ε保持不变，结合了ε-decreasing方法中ε衰减的特点，同时也具有ε-贪婪方法在每一幕步数中ε保持不变的特点。在选择同时满足上述两个特点的ε衰减函数上，采用式(4)控制ε值的衰减。

(4)

其中，ε0为贪婪系数的初始设定值，0<ε0≤1，episode为幕数变量。

将式(4)与式(1)结合可得式(5)。

2.2.2 AεBS方法

根据到达位置的陌生/熟悉程度和动作价值，从而做出探索/利用的动态动作选择AεBS方法。引入不断学习更新的Q表中动作价值作为陌生/熟悉程度的指标，当状态s下所对应的所有动作价值全为0时，认为该状态对于智能体来说是陌生的；当状态s下所对应的所有动作价值不全为0时，认为该状态对于智能体来说是熟悉的。在每幕学习的每一个步(step)中，遇到陌生的位置状态，ε值变为1，采取探索模式随机选择动作集中的任一动作；遇到熟悉的位置状态，ε值变为0，采取利用模式选择状态动作价值最大的动作。另外融合ε-first方法的思想，根据未知环境情况的不同，在幕数段中加入很小的ε值对Q表更新进行微调整。可用式(6)表示：

(6)

其中，episode为幕数变量,episo1和episo2为设定的幕数值，ε0为贪婪系数的初始设定值，0<ε0≤1，A(s)为状态s下的动作集合。

由于初始阶段中Q表的动作价值均初始化为零，因此采用AεBS方法的智能体可以充分探索环境，即每当遇到动作价值为零时智能体会判断出自身处于陌生环境，更倾向于随机选择不同的动作进行探索，更有可能不断遇到陌生情况，探索更为充分。同时在与环境的交互中不断更新Q表的动作价值，增加环境熟悉程度，从而利用Q表的动作价值的大小比较选择最优动作，进而不断更新路径策略。

3 引入εDBE方法和AεBS方法的Q学习路径规划

在未知环境路径规划下，移动智能体在不同的状态s下通过策略π选择要采取的动作a，与环境进行交互获得奖励r，并到达下一状态s'。重复上述过程不断迭代探索，更新Q表中的动作价值，找到更好的动作，直至找到最优策略π*，完成未知环境下的路径规划。时序差分方法是评估价值函数和寻找最优策略的实用方法。时序差分方法可以使智能体能直接与环境互动的经验中学习，不需要构建关于环境的动态特性。

Q学习是off-policy下的时序差分控制方法，是强化学习的一个重要突破[14]。Q学习更新的是动作价值函数，更新方法如式(7)所示：

Q(st,at)←Q(st,at)+α[rt+1+

γmaxaQ(st+1,a)-Q(st,at)]

(7)

其中，α为学习率，0<α<1；γ称为折扣因子，表示未来奖励对当前状态的影响程度[15]，0≤γ≤1。

在t时刻智能体处于状态st，动作状态价值为Q(st,at)，当智能体采取动作at后在t+1时刻到达状态st+1并获得奖励rt+1，此时智能体将在Q表中找到能够使在状态st+1下动作价值最大的动作a,以此来获得Q(st+1,a)，从而对Q(st,at)进行更新。

可将式(7)改写成式(8)。

Q(st,at)←(1-α)Q(st,at)+

α[rt+1+γmaxaQ(st+1,a)]

(8)

假设st+1所对应的maxaQ(st+1,a)恒定，通过式(8)可迭代求得稳定的Q(st,at)。

一次迭代：

Q(st,at)←(1-α)Q(st,at)+

α[rt+1+γmaxaQ(st+1,a)]

(9)

二次迭代：

Q(st,at)←(1-α)[(1-α)Q(st,at)+

α[rt+1+γmaxaQ(st+1,a)]]+

α[rt+1+γmaxaQ(st+1,a)]

←(1-α)2Q(st,at)+

[1-(1-α)2][rt+1+γmaxaQ(st+1,a)]

(10)

以此类推，n次迭代：

Q(st,at)←(1-α)nQ(st,at)+

[1-(1-α)n][rt+1+γmaxaQ(st+1,a)]

(11)

因为0<α<1，所以0<1-α<1，当n→∞时，Q(st,at)将以概率1收敛到最优值，即：

Q(st,at)←rt+1+γmaxaQ(st+1,a)

(12)

当Q表更新后，根据式(13)即可选出状态下具有最大动作状态价值的动作，从而获得路径规划更优策略π'的更新。

π'(s)=argmaxaQ(s,a)

(13)

该文以稀疏奖励的形式定义奖励函数r，如式(14)所示，将状态分为障碍状态、路径状态和目标终点状态，分别用状态集合O(s)、P(s)、G(s)表示。其中到达障碍状态获得-1奖励值，到达目标终点状态获得+1奖励值，到达路径状态获得0奖励值，促使智能体避开障碍物快速到达目标终点。

(14)

每个状态有上、下、左、右四个动作可选择，训练的过程为输入当前状态后，根据(εDBE)方法或根据(AεBS)方法从Q表中选出当前状态的相应动作，与未知环境交互后获得奖励，进入下一状态并判断是否撞到障碍物。

若判定会撞到障碍物,则根据式(8)更新Q表后结束本幕学习，开始下一个幕的学习;若判定不会撞到障碍物,则根据式(8)更新Q表后进入下一状态,本幕学习直至到达终点或判定会发生碰撞障碍物后结束。重复学习过程,不断更新Q表中各个状态的动作价值，直至找到最优策略，实现路径规划。

4 实验结果及分析

4.1 实验设计

该文在10*10的地图上进行Q学习路径规划，设定了两种智能体未知的不同环境，对提出的基于探索-利用权衡优化的Q学习路径规划与基于经典的ε-贪婪方法、ε-first方法、ε-decreasing方法的Q学习路径规划进行比较，验证提出方法的可行性和高效快速性。

其中每个网格对应一个状态，用不同的状态标号表示[16]。即在位置(x,y)处的网格对应的状态标号stateno可用式(15)表示。

stateno=10(x-1)+y

(15)

图3所示为两种智能体未知的情况地图，状态SS为起点位置，GS为终点位置，起始位置和路径均用深灰色表示，黑色为障碍物。智能体在每个无障碍物的浅灰色位置状态下，有上、下、左、右四个动作可以选择，碰到障碍物意味着一幕学习以失败结束，获得-1奖励值，并返回起点位置；到达终点意味着一幕学习以成功结束，获得+1奖励值，并返回起点位置；到达其余状态均获得0奖励值。

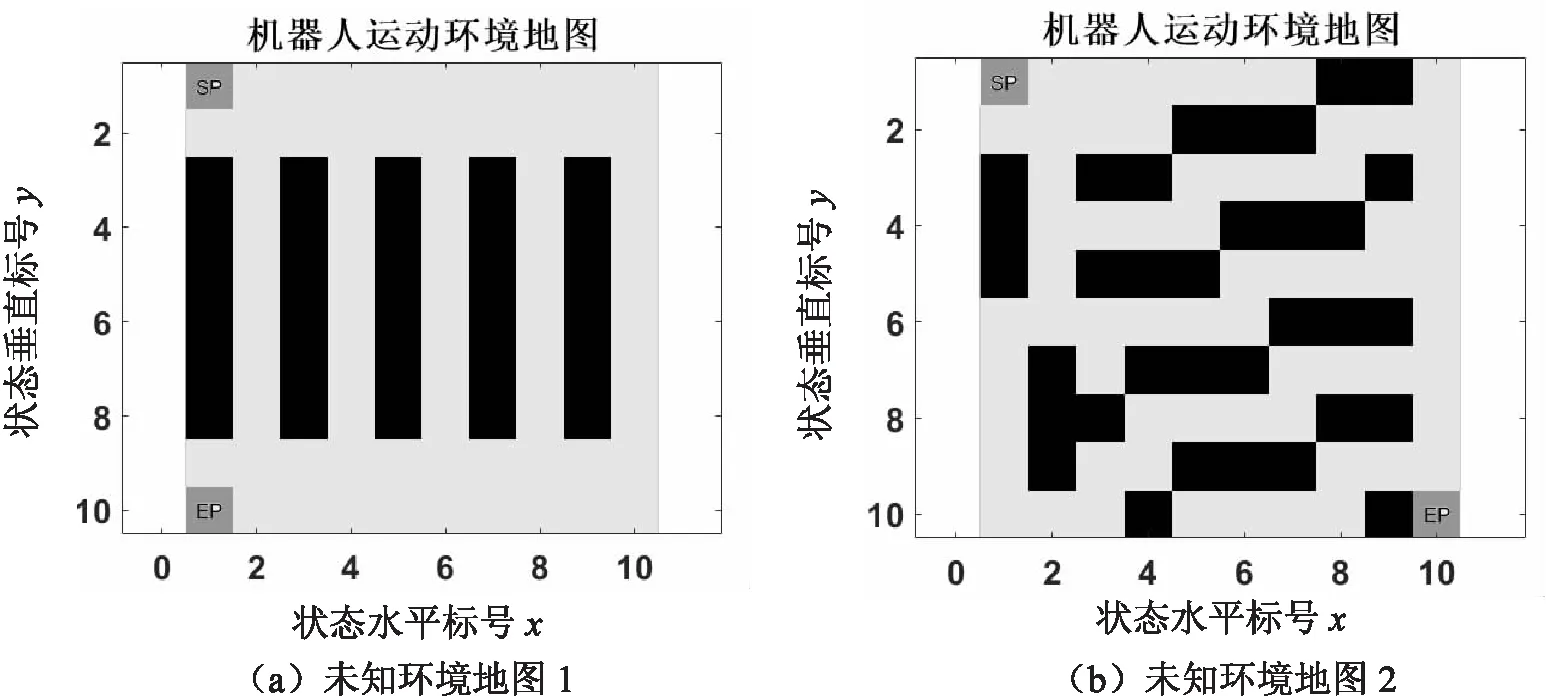
图3 两种智能体未知的环境地图

4.2 结果分析

通过Q学习路径规划可以得到以下仿真实验结果：图4所示为未知环境地图1下的仿真实验结果，其中折扣因子γ=0.8，学习率α=0.2，ε-贪婪方法的ε值为0.1，ε-decreasing方法的ε初始值为0.8，εDBE的ε初始值为0.2，AεBS方法在30幕前的ε值为0.05。从图4(b)可以发现，Q学习可以实现路径规划，找到从起点到终点的最优路径，状态转移步数为11步。

图4 未知环境地图1中的仿真实验结果

从图4(c)不同方法不同幕下ε变化比较中，ε-decreasing方法中ε衰减过程较为波动，εDBE方法中ε衰减过程较为平缓。

从图4(d)不同方法路径成功率比较中可以看到，提出的(εDBE)方法和(AεBS)方法都比经典的ε-贪婪方法、ε-first方法、ε-decreasing方法能更快找到最优路径，在相同的幕数经验学习下成功率更高。

从图4(e)不同方法路径步数收敛变化比较中也可以看出，(εDBE)方法和(AεBS)方法最优路径收敛更快，ε-贪婪方法大约在170幕左右收敛、ε-first方法大约在110幕左右收敛、ε-decreasing方法大约在100幕左右收敛，(εDBE)方法和(AεBS)方法大约在60幕左右收敛。

在图4(f)不同方法路径步数收敛后方法特性比较中，由于(εDBE)方法和ε-贪婪方法中ε-值不为零，会出现一些细小的探索“尖刺”，但这些额外探索并不会妨碍智能体根据Q表中动作价值函数找到最优路径。

为了检验不同未知复杂环境下基于探索-利用权衡优化的Q学习路径规划方法的适应性，在未知环境地图2下继续进行仿真实验，其中折扣因子γ=0.8，学习率α=0.2，ε-decreasing方法的ε初始值为0.8，εDBE的ε初始值为0.2，AεBS方法在100幕到300间的ε值为0.1。

图5所示为未知环境地图2下的仿真实验结果。实验结果表明，提出的(εDBE)方法和(AεBS)方法较ε-first方法、ε-decreasing方法，在Q学习路径规划中依然能更有效快速找到最优路径，状态转移步数为20步，最优路径收敛所需的学习幕数更少，找到路径的成功率更高。

图5 未知环境地图2中的仿真实验结果

5 结束语

针对移动智能体在未知环境下的路径规划问题，提出了基于探索-利用权衡优化的Q学习路径规划。实验结果表明，该方法具有可行性和高效性：提出方法能找到最优路径，实现路径规划；与现有的权衡探索-利用的ε-贪婪方法、ε-first方法、ε-decreasing方法比较，提出的(εDBE)方法和(AεBS)方法能更好权衡探索-利用问题，在未知障碍环境情况下具有快速学习适应的特性，最优路径步数收敛速度更快，能高效可行地解决未知环境下的路径规划问题。