多种因素影响下钨合金破片的穿甲深度研究

舒张忆南，梁争峰，阮喜军，何 勇

(西安近代化学研究所，西安 710065)

1 引言

防空反导导弹大多以破片杀伤战斗部为主要毁伤元，通过装药爆炸来驱动产生的破片群，利用破片的动能来对目标进行侵彻毁伤。因此，评估破片杀伤战斗部的毁伤威力的一个重要指标就是破片的穿甲深度，也就是在一定的参数下破片能贯穿多厚的装甲防护。影响这个指标的因素有很多，包括破片的质量、形状、着靶速度等等，研究这些参数对破片穿甲深度的影响具有重要意义，可以为战斗部的设计提供参考。

在选择材料时，钨合金由于其具有密度大、存速能力好、穿透性强等一系列特点，在杀伤战斗部破片材料中占据了很大一部分比重。许多研究者都对钨制破片的性能进行了研究，唐娇姣研究了钨合金破片力学特性与爆轰驱动破碎行为的关联性，用动态力学性能分析和金相研究结合预估了破片的爆轰驱动破碎行为；王祝波等利用数值模拟的方法研究了钨破片形状对穿甲速度的影响，得到了立方形破片速度、动能在穿甲过程中衰减最大的结论；赵小峰研究了破片质量对钨合金破片侵彻威力的影响，通过理论计算、数值仿真和试验验证相结合，得出了随着破片质量的增大，破片最大侵彻深度逐渐增加，但增大率减小的结论；谭多望等对球形钨合金破片终点弹道性能进行了实验研究，总结了钨珠长距离飞行时的速度衰减规律并修正了侵彻靶板后剩余速度计算公式；弗劳恩霍夫实验室的Patrick Frueh等人对含钴和不含钴2种不同成分的钨合金破片的终点弹道性能进行了比较，发现钨合金的成分对破片穿甲深度具有相当大的影响；土耳其TOBB大学的Hakan Hafizoglu等则考察了烧结温度和Ni/Fe比对液相烧结钨重合金破片弹道性能的影响，结果表明一定烧结温度下的钨合金破片穿孔性能最好，过高或过低的温度都会影响穿甲能力。但是目前综合考虑多种因素同时作用的情况，并且比较这些因素对穿甲深度的影响效果的研究者还比较少。

本文通过理论计算和利用LS-DYNA进行数值模拟计算的方法研究在质量、形状和着靶速度等多种因素的共同影响下，钨制(93 W)破片侵彻Q235装甲钢的穿甲深度变化情况，总结各因素对穿甲深度的影响规律，找出对穿甲深度影响较大的因素，修正穿甲深度的计算公式并通过静爆实验来验证修正后的公式。

2 静爆试验

为了研究钨合金破片的穿甲深度，设计了不同破片参数的杀伤战斗部样机，采用地面静爆打靶试验的手段，来获取破片的穿甲深度参数。试验现场布局如图1所示。

在距爆心12 m处沿圆弧连续布设Q235钢靶，高度为5.5 m，弧长为7.5 m，钢靶由几块厚度分别为10 mm、12 mm、14 mm、16 mm等依次递增的靶板组成。

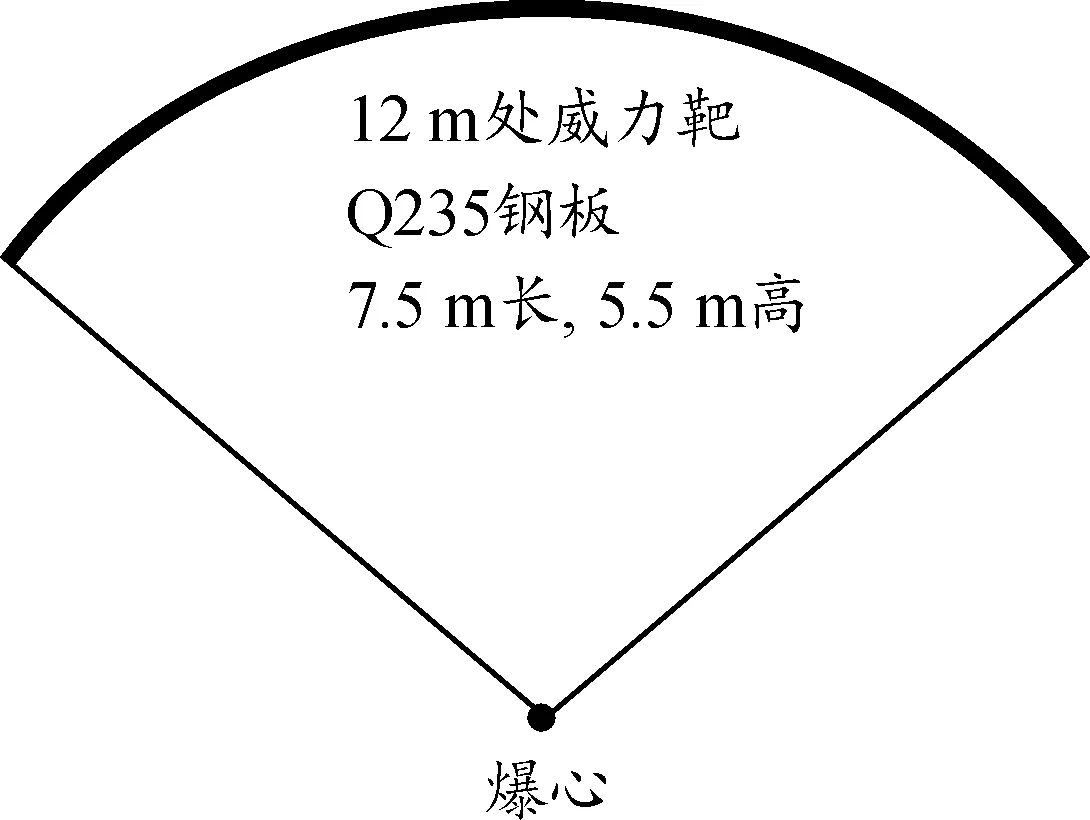
图1 试验现场布局示意图

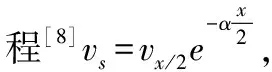
破片在靶板上的穿孔如图2所示，收集了几组不同情参数下的破片穿甲深度数据，静爆试验结果如表1所示。

图2 靶板破片穿孔示意图

表1 静爆试验结果Table 1 Static explosion test results

3 数值模拟计算

3.1 建立计算模型

因地面静爆试验只能得到有限几种工况下的破片穿深数据，要进行深入研究，需要使用LS-DYNA软件对钨制破片在多种影响因素下的穿甲深度进行数值模拟仿真。

破片材料使用93W钨合金，查阅文献[9]可知其密度=17.6 g/cm，同时考虑到质量、形状和着靶速度等因素，选择的破片种类有9种，分别是直径为Ф6.88 mm、Ф8.16 mm和Ф9.54 mm的钨合金球，直径为Ф4.77 mm、Ф5.66 mm和Ф6.61 mm，长径比为2∶1的钨合金圆柱，以及边长分别为5.54 mm、6.57 mm和7.69 mm的钨合金立方体，3种大小破片的质量分别约为3 g、5 g和8 g。这些破片分别以一定的着靶速度侵彻装甲钢靶板，着靶速度从1 000 m/s开始依次增加500 m/s直到3 000 m/s。装甲钢靶板的材料选择Q235钢，查阅文献[10]后得到，Q235钢的杨氏模量=200 GPa，泊松比=0.3，比热容=469 W/(m·K)，密度=7 800 kg/m，熔化温度=1 795 K。靶板采用半无限靶，边长为100 mm，厚度为200 mm，考虑到破片尺寸与靶板尺寸相比为小量，靶板可以认为是无限区域，对靶板施加非反射边界条件。由于模型具有轴对称特性，为简化计算可以取1/4模型，然后对1/4分割面上所有节点施加对称面法相约束。破片和靶板均采用Lagrange算法，六面体网格划分，计算模型如图3所示。

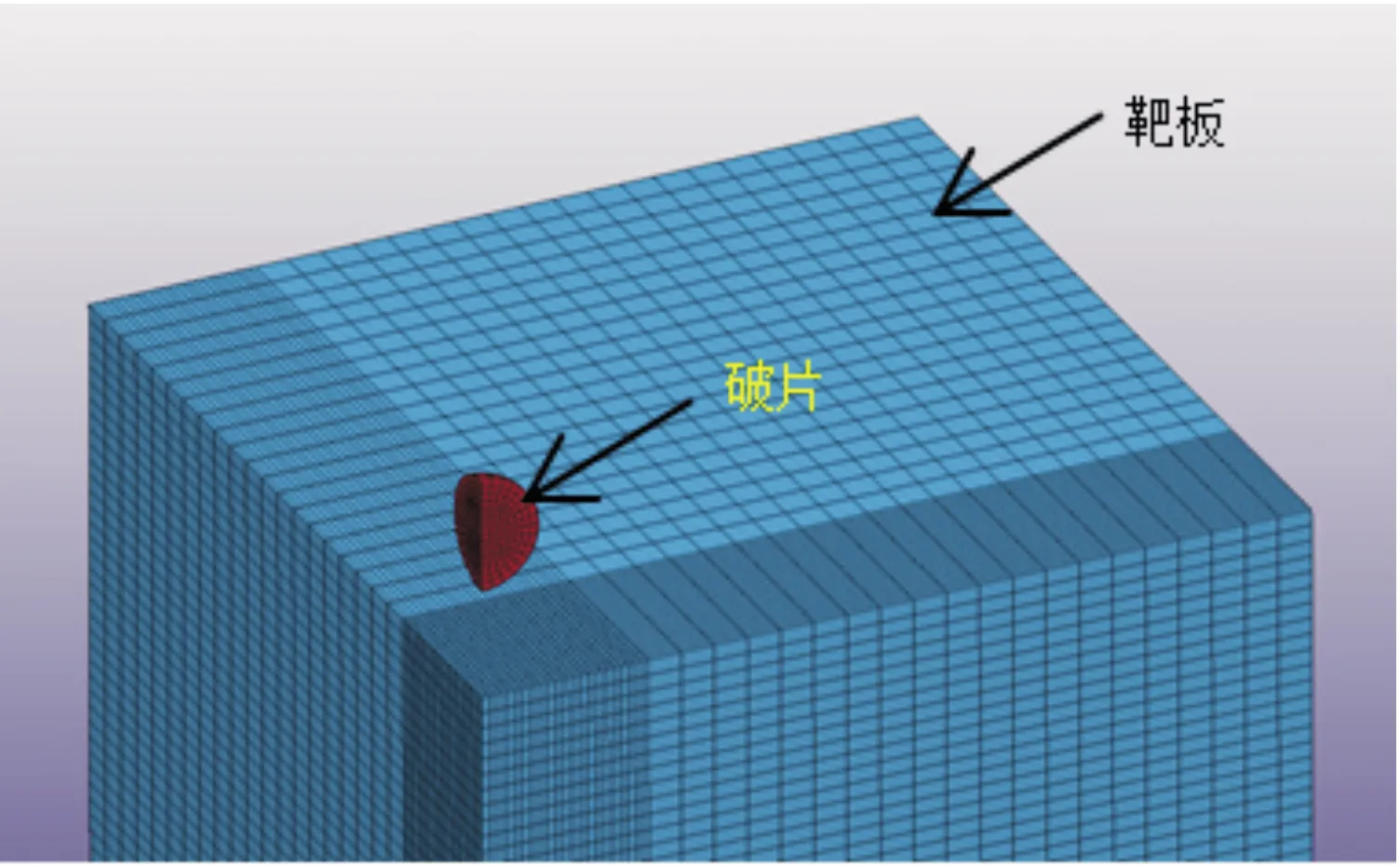
图3 数值仿真计算模型示意图

破片和靶板在侵彻过程中互相挤凿破坏，因此需要用面面冲蚀接触(CESTS)来定义破片与靶板之间的接触类型，并且由于这个过程伴随着大变形、高应变率和高温，需要用Johnson-Cook本构模型和Gruneisen状态方程模型来描述破片和靶板。模型各参数如表2和表3所示。

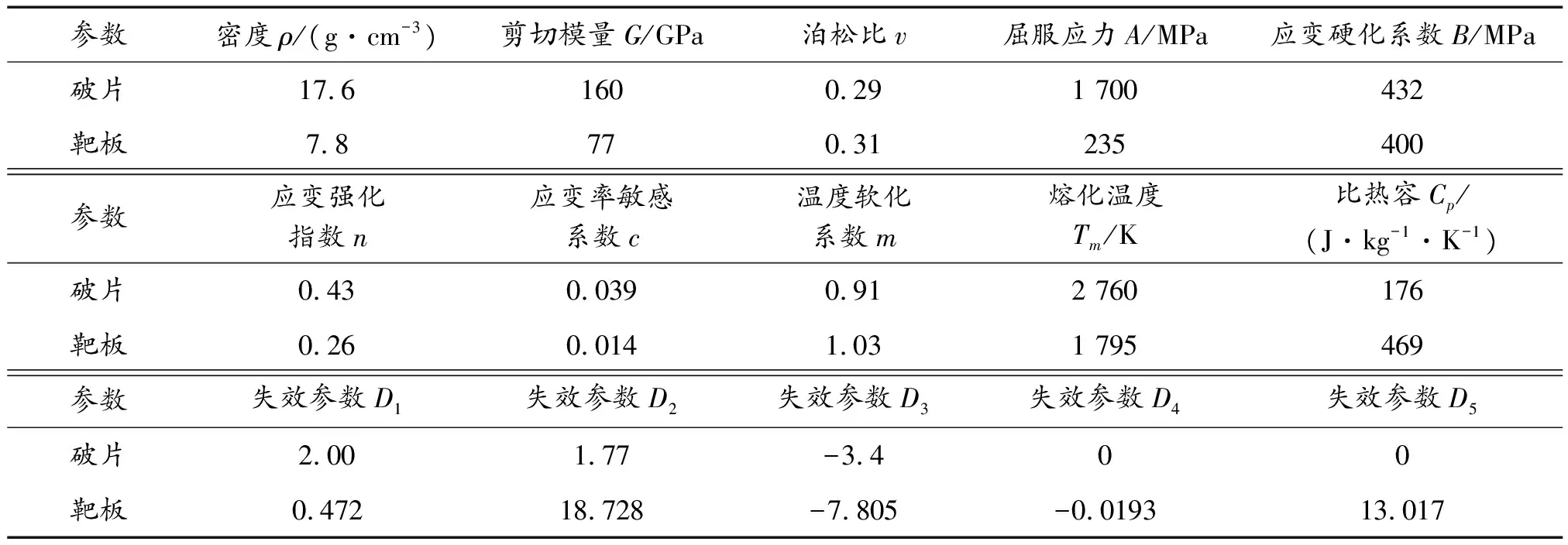
表2 Johnson-Cook本构模型相关参数Table 2 Related parameters of Johnson-Cook constitutive model

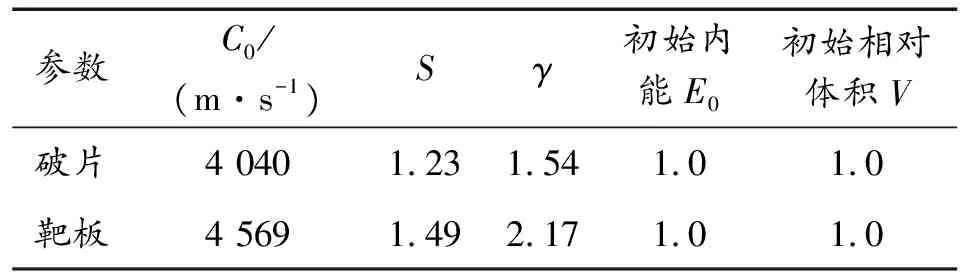
表3 Gruneisen状态方程模型相关参数Table 3 Related parameters of Gruneisen equation of state model

3.2 计算结果分析

在数值模拟破片侵彻靶板的过程中，破片着靶后在惯性和靶板压力的作用下发生冲蚀和塑性变形，逐渐扁平化，边缘向外扩散并向上弯曲，着靶速度越大现象越明显，高速时呈现一个中间凹陷四周向上蜷曲的状态，过程中有一定的质量耗损，速度越大耗损越严重。同时靶板也发生冲蚀和塑性变形，形成一个尺寸随深度而减小的穿孔，初始尺寸明显大于破片着靶面积。3种破片着靶时和侵彻结束时的典型形态如图4所示。

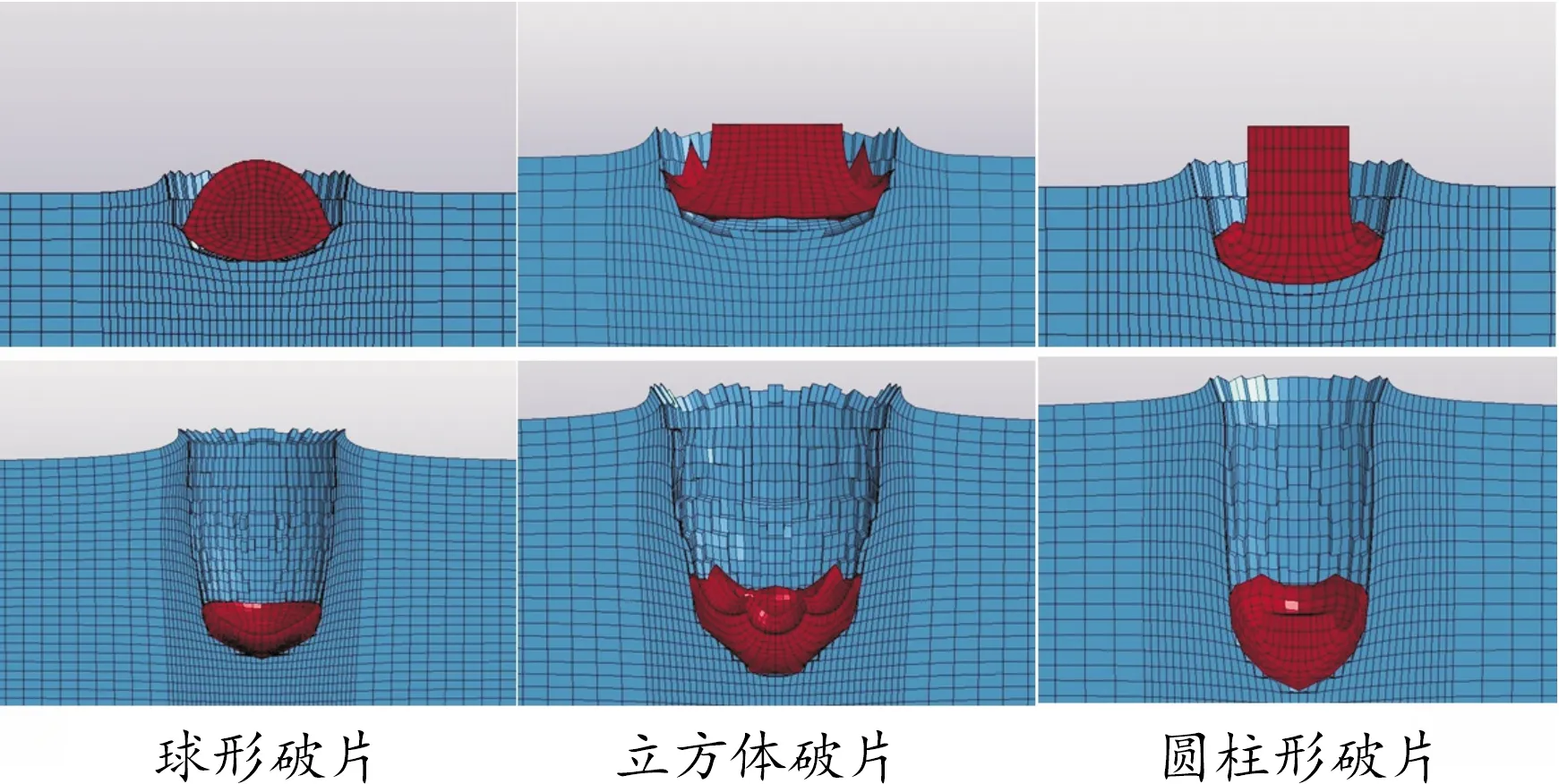
图4 3种破片着靶时和侵彻结束时的典型形态示意图

数值模拟计算得到的不同情况的穿甲深度如表4所示,根据表4分析可知，3种影响因素中，在其他条件相同的情况下改变破片形状更容易对穿甲深度造成较大的影响，改变破片着靶速度次之，改变破片质量对穿甲深度的影响最小。破片穿甲能力主要取决于破片自身的动能大小，破片形状主要影响了破片的着靶面积，着靶面积越小破片受到的阻力越小，因此动能损耗也小导致穿甲深度增大，如图5所示，圆柱形破片速度损耗最小，因此同等条件下穿甲深度最大。而增大质量在动能提高的同时也增大了着靶面积，导致穿甲深度的增加不明显，如图6所示。

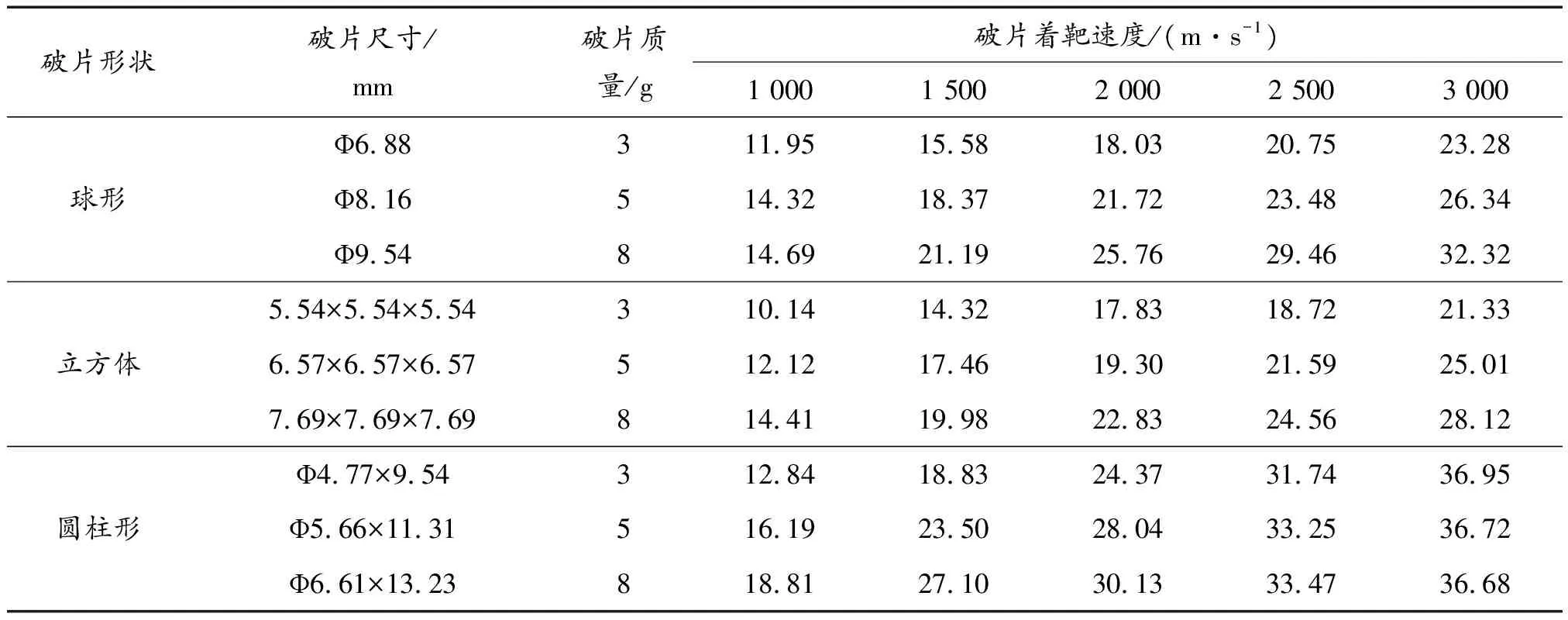
表4 破片穿甲深度仿真计算结果(mm)Table 4 Simulation results of fragment penetration depth

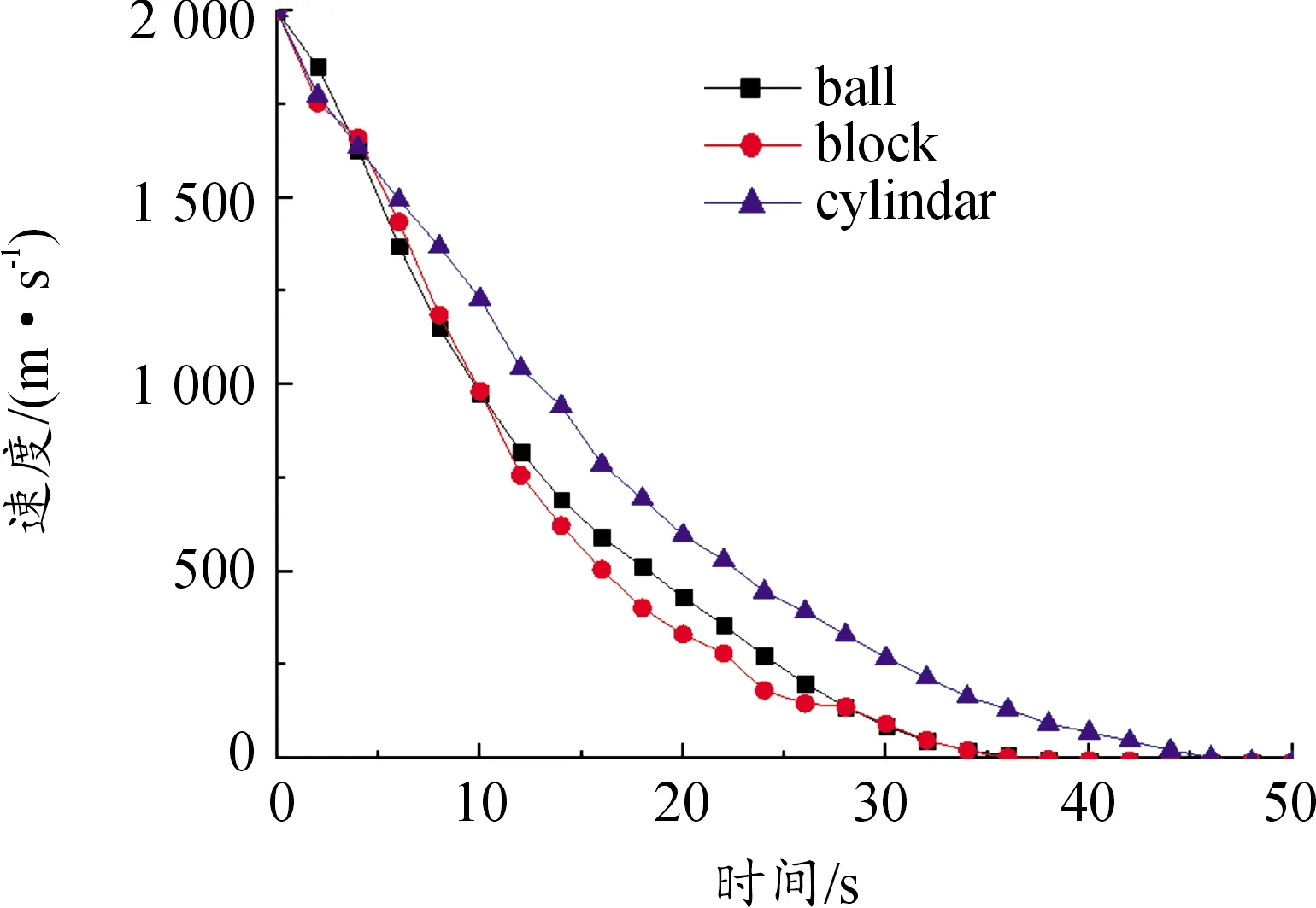
图5 不同形状的5 g破片在着靶速度为 2 000 m/s时的速度时程曲线

4 理论分析与计算

4.1 破片穿甲深度计算

破片穿甲深度的计算公式可以通过破片剩余速度公式推导得到，计算破片剩余速度通常采用基于大量实验数据总结而成的THOR经验公式，表达式如下：

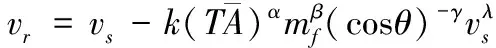
(1)

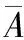
在不考虑着靶角度的影响时，破片均为正撞击靶板的状态，即=0。根据式(1)可以推导，当破片剩余速度=0时，此时的靶厚就是破片在着靶速度为和质量为的情况下的破片穿甲深度，表达式为

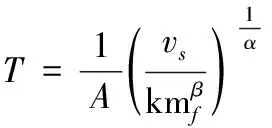
(2)

根据文献[8]，低碳钢靶板相关参数分别为=5 791 m/s、=0.906和=-0.963，代入式(2)可计算得到选择的9种破片在1 000～3 000 m/s速度范围内的破片穿甲深度。

4.2 计算结果及分析

根据式(2)得到了9种破片的穿甲深度，结果如表5所示。

与数值模拟计算的结果对比，理论计算得到的穿甲深度普遍较大，尤其是立方体和圆柱形这2种形状的破片，这是由于理论计算公式中没有考虑到破片的形变和侵彻过程中质量损耗对穿甲深度的影响。低速时球形破片形变不是十分明显，由形变所导致的动能损耗较小，因此穿甲深度的数值模拟计算和理论计算结果相差较小，而立方体破片和圆柱形破片在侵彻过程中发生较大的形变，造成更大的动能损耗。高速时由于破片质量损耗严重，穿甲深度的数值模拟计算结果增幅变小，导致与理论计算结果相差巨大，理论计算公式结果不再适用。

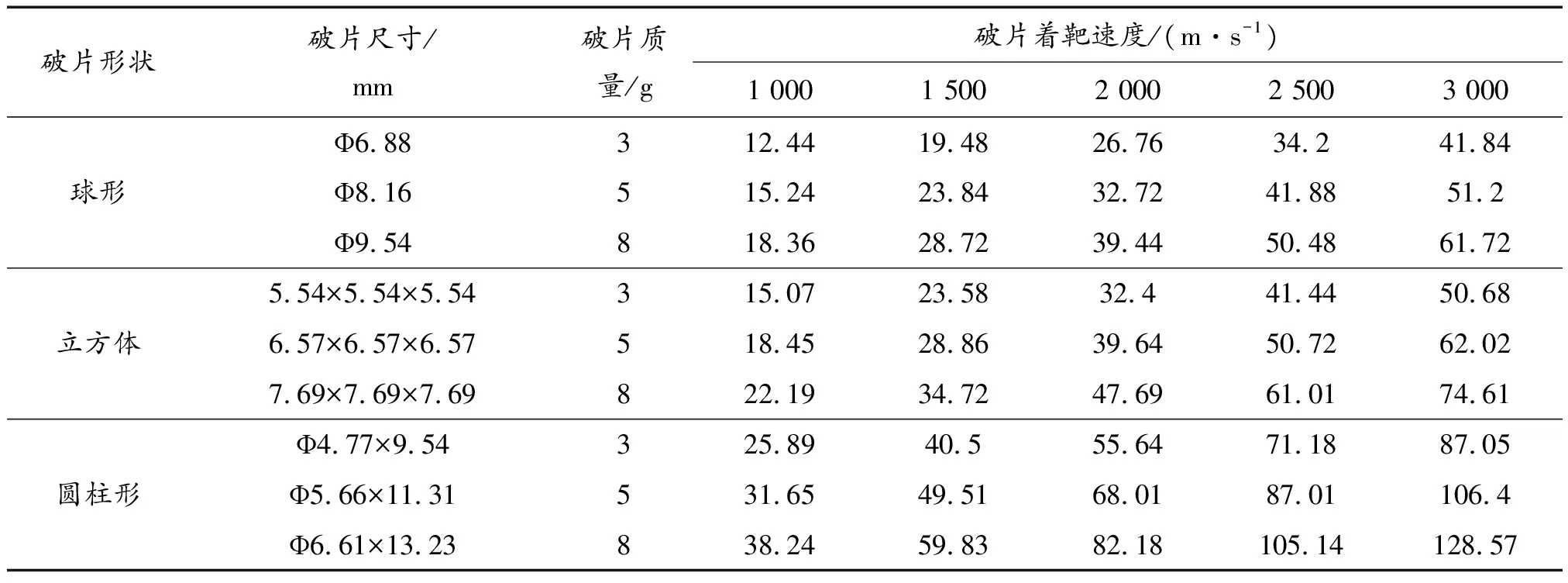
表5 破片穿甲深度理论计算结果(mm)Table 5 Theoretical calculation results of fragment penetration depth

4.3 理论计算公式修正

为了使理论计算的结果与数值模拟计算的结果符合，需要对破片穿甲深度的理论计算公式进行修正，添加形状修正系数，改变速度和质量影响系数。修正后的计算公式形式如下：

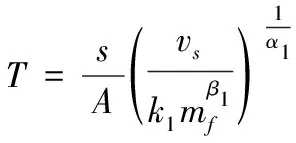
(3)

式(3)中：为形状修正系数，、和分别为修正后的速度和质量影响系数，其他参数含义与式(1)、式(2)相同。

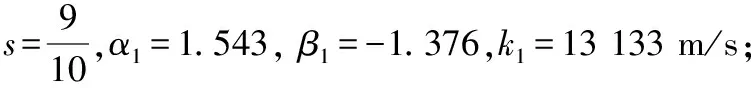
因此，修正后的93W钨合金破片穿甲深度计算公式如下：

(4)

为了验证修正后的理论计算公式的可靠性，将理论计算、数值模拟仿真和静爆实验的结果进行对比，如表6所示。结果表明除了一组数据之外其他数据的误差都在5%之内，证明了数值模拟和修正后的理论计算公式的有效性。

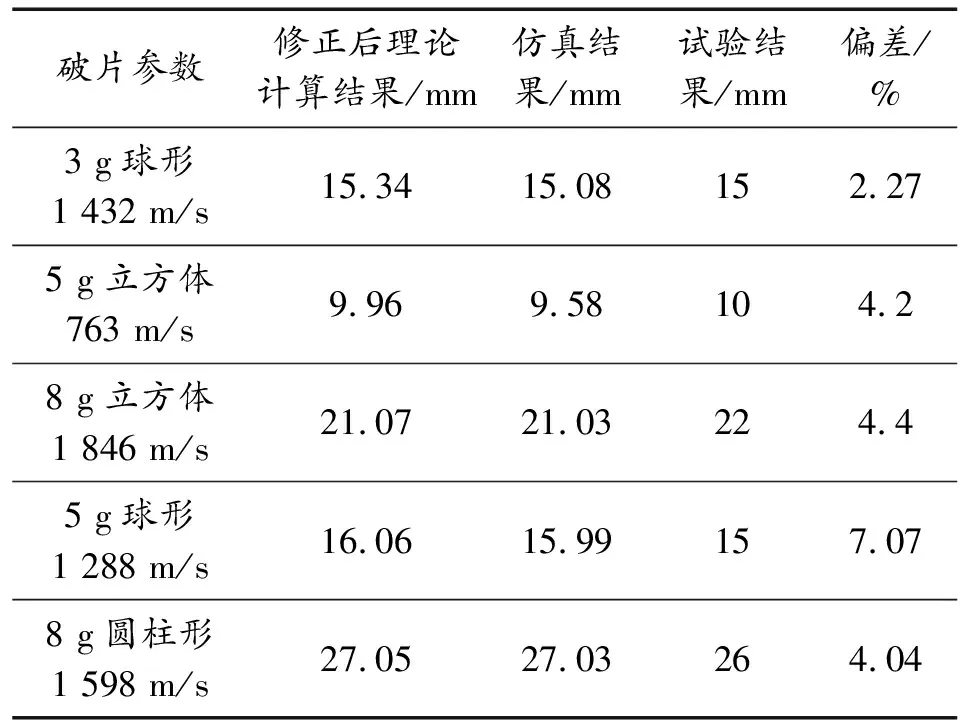
表6 试验结果及比对Table 6 Test results and comparison

5 结论

1) 钨合金破片侵彻Q235钢靶时，用改变破片形状的方法来增大破片的穿甲能力是最容易且有效的。在破片质量和着靶速度都相同时，长径比为2∶1的圆柱形破片穿甲深度平均是立方体破片的1.3～1.5倍，在高速情况下差距更为明显。如果无法保证圆柱形破片合适的着靶角度，破片的穿甲能力会大幅降低，所以仍然推荐使用穿甲能力稳定的球形破片。

2) 破片质量和着靶速度比较，按相同比例增大破片着靶速度可以更为有效地增加破片的穿甲深度。