计及可调负荷定价的预期交易时间优化分析
周涛,钱寒晗,张纬,胡涛,李生虎
(1.国网安徽电力公司电力交易中心,安徽 合肥 230061;2.合肥工业大学电气与自动化工程学院,安徽合肥 230009)
0 引言
随着“双碳”目标提出,新能源并入电网容量增加,其随机波动性给电网安全运行带来挑战[1]。构建源网荷储一体化新型电网是解决方法之一,但是储能投资较大[2]。合理利用需求侧响应,可减轻电力平衡压力,提高电网消纳可再生能源的能力。如何建立可调负荷交易机制,值得进一步研究[3]。
可调负荷分为可削减负荷、可转移负荷和可平移负荷[4]。现有文献往往将可调负荷包含在整个市场体系中[5],很少单独分析其交易机制。在日前市场,用户采用时间序列、神经网络、回归分析、模糊预测等[6-8]方法,预测可调负荷量,参与需求响应以减小供电缺额、增加收益[9-10]。
可调负荷定价受电价政策、负荷类型、节假日、气温气候、生活或工作习惯等因素影响[11-12]。文献[13]以电量成本和容量成本建立负荷成本,未考虑外在因素影响。文献[14]在电力成本基础上,考虑参与调节导致用户满意度降低的损失成本,但未计及需求关系对定价的影响。文献[15]考虑电价弹性对负荷定价的影响,仅适合采用分时定价策略的市场。文献[16]研究了多时间尺度调度策略,将调度日划分为不同时段,协调源、荷资源,以发挥负荷响应潜力。
理论上,可调负荷与售电公司确定交易的时间越早,售电公司和用户可越早对负荷进行规划,可调负荷的调度成本越低,报价越低,同时市场越稳定。但是确定交易时间越早,负荷预测偏差期望值越大,惩罚费用越高。因此需要优化以确定交易时间,降低考虑可调负荷价格和偏差惩罚的售电公司总成本,对此未见文献研究。
为了增加市场弹性,本文基于负荷预测精度与交易时间的关系、可调负荷成本、负荷预测偏差惩罚价格,提出一种以售电公司总成本最小为目标的优化模型,以确定最优交易时间。并给出计算分析结果,以验证算法的可行性。
1 负荷预测偏差与交易时间的关系
1.1 负荷的预测模型
预测负荷,提前规划辅助服务市场,确定可调负荷的交易,可避免可调负荷的浪费,缩小负荷峰谷差,以辅助实时市场调度。同时考虑可调负荷随机性和用户利益,增加需求侧响应的积极性,本文提出一种提前规划、交易可调负荷的方法。
可调负荷的实际调节量由两部分组成,一部分为确定交易时预测的负荷调节量,其根据源网平衡及用户参数确定,非本文研究内容;另一部分为实际调度时,由于负荷随机性导致的预测偏差。以历史负荷实际值与预测值间偏差的期望值模拟预测偏差,进行优化计算。这两部分的确定均依赖于负荷的预测模型。负荷预测的准确性是用户参与市场调节的前提。以下参考江苏现试行的电力市场用户可调负荷参与辅助服务市场交易规则[17],改进现有负荷预测模型。
在工作日、周末和节假日,负荷水平存在差异。周末居民负荷明显上升;在春节等节假日,受人口流动影响,市区居民负荷下降。部分企业在周末和节假日休息,负荷显著减少。商业负荷在周末和节假日增加[18]。以下区分时间段,针对不同类型负荷,以交易日前的实际负荷预测调度日的负荷。其中调度日是可调负荷实际参与调节的日期,交易日是售电公司提前预测交易的时间,定义交易日与调度日间的间隔为预期交易时间TTI。不同时间段,TTI的表示方式不同。
1)在工作日,TTI以工作日为单位表示。考虑每周负荷周期性,根据前5个工作日平均负荷、相较再前5个工作日负荷的增长率,来预测负荷。因此,预测工作日负荷如下:

式中,PL为实际负荷,下标F表示其预测值;分别为交易日前1~5个工作日和前6~10个工作日的平均负荷,下标D表示工作日;e=1+TTI/5,将周的电量增长率换算至对应工作日天数的增长率指数。
2)在周末,用前两周周末平均负荷和该周工作日用电量增长率,预测负荷见式(2),其中为交易日前2个周末平均负荷,下标W表示周末。
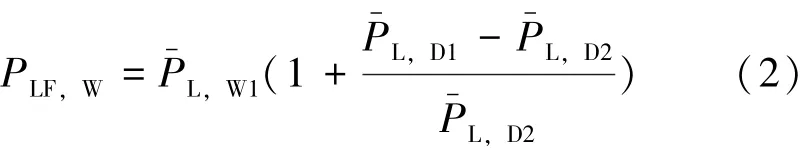
3)法定节假日往往每年仅一次,仅凭上年同期负荷预测不准确。因此,还考虑上个可类比节假日负荷,得到节假日负荷预测值:

1.2 预测偏差拟合曲线
TTI越小,预测间隔越小,预测越准确,预测偏差越小;而TTI越大,负荷随机性越大,预测偏差越大,故预测偏差和TTI间关系可用一定数学规律描述。采用最小二乘法[19]建立预测偏差与预期交易时间的关系。
与实际值PL相比,预测负荷的偏差ΔPLF为:

假设已知28天24 h的负荷历史数据,其中工作日有20天,如图1所示。基于式(1),需10个工作日的数据进行预测,假设TTI=3,则第11天可用1~10天数据预测第14天的负荷,以此类推得到该交易时间下的24g(g=20-10-TTI=7天)个预测数据。与相应实际值相减得到24g个预测偏差,计算均值得到该交易间隔下的预测偏差,从而得到不同预期交易时间的负荷预测偏差。

图1 预测偏差计算过程
采用最小二乘法,以n次多项式y(x)=a0+a1x+…+an xn拟合预测偏差ΔPLF与预期交易时间TTI间的关系曲线。其中(xi,yi) 表示已知点,xi表示TTI,yi为对应ΔPLF,i=1,…,m,m表示点个数。选择系数a0,a1,…,an,以拟合误差平方和最小为目标:

以上非负二次多项式,必存在最小值。在其最小值处,式(5)对各系数偏导为0,得:

据式(7),简记上式为A T Aa=A T Y。由式(8)可解得系数a,得到负荷预测偏差与预期交易时间的曲线。


2 预期交易时间的优化
综合考虑可调负荷交易价格和预测偏差惩罚,以确定售电公司总成本,如图2所示。上文已得到预测偏差与预期交易时间的关系。为得到可调负荷交易价格,首先应确定可调负荷的定价策略。
图2售电公司总成本的计算流程
以下参考储能和火电定价模型[20],考虑负荷调节成本E,定义可调负荷定价Q,见式(9),其中R表示可调负荷相关系数,受多个因素的影响,以下依次介绍。

调节成本E包括固定成本E1和可变成本E2,见式(10)。固定成本主要为运维成本,包括参与电力调度引起的负荷设备成本及损耗,以及运维人员工资成本等。E2包括调度成本CS和补偿成本CC[13]。
调度成本包括两部分:一部分为规划改变负荷消耗的成本,越临时调度负荷,所消耗成本越大;另一部分为由于参与可调负荷造成用户减少的损失[14],越早规划告知用户可减少损失。两者均与预期交易时间呈负相关,根据实际零售市场运营经验,选用反比例函数假设更准确,见式(12),其中b为常数。

补偿成本CC指售电公司对用户的补偿,分别以用户可调负荷容量和其参与调节的电量进行补偿,表示为容量成本CTAL(元/MW)和电量成本CAL(元/MW·h):

式中,PTAL、PALF分别为用户可调负荷容量和负荷调节量的预测值,TAL为可调负荷的调度时长,下标AL表示可调负荷。
相关系数R主要受需求关系(F1)、国家政策(F2)及日历因素(F3)影响。考虑供需-价格的市场规律,可调负荷定价与需求呈正相关,即可调负荷需求量越大,价格越高,反之亦然。而需求量由用户可调负荷容量和负荷调节预测值间的差值表示,差值越小,需求越大。参考文献[21],选用线性函数近似表示F1式(14),其中参数c、d表示电力市场需求特性。

国家可能通过宏观调控手段对可调负荷进行补贴,取补偿方式S2(单位为 元/(MW·h))如下[16]:

式中,常数P1、P2分别为补偿初始门槛功率和最大门槛功率。故F2的计算见式(16),其中η表示利润率。

考虑工作日、周末以及节假日的用电差异,不同时间段、不同负荷类型、不同行业,负荷增长系数不同。以第三产业为例,随着用电负荷变化,可调负荷相应变化。假设负荷增长系数F3如下:

取λF1、λF2、λF3分别为需求关系、国家政策、日历因素对定价影响的权重系数,且λF1+λF2+λF3=1,系数的确定方法见文献[20]。考虑从成本到价格过程,构造R计算式如下:

综上,考虑预期交易时间和预测偏差,定义售电公司总成本C,见式(19),前半部分为可调负荷交易价格,以可调负荷报价和预测的可调负荷量的乘积确定;后者为预测偏差惩罚价格,由预测偏差乘以惩罚价格得到,其中CP为预测偏差的惩罚价格。
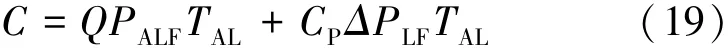
确定交易时间越早,可调负荷报价越低,可调负荷交易价格越低,但相应预测偏差惩罚价格越高。故以售电公司总成本最小为目标建立优化模型,以优化预期交易时间。
预期交易时间越久,负荷随机性增大,负荷预测偏差越大,不利于系统稳定运行,故综合考虑现有零售市场的结算时间和可调负荷预测误差,对预期交易时间的最大值进行限制,其范围如式(20)所示,为优化模型的不等式约束。

前文中引入变量均为优化目标中参数,其中报价参数见式(12),与交易时间存在关系,故式(9)—(18)均为优化模型中的等式约束。综上,优化模型表示为式(21)。

对不同用户,负荷约束值不同,故在算例中通过列举不同的负荷调节量、用户可调负荷容量以及可调负荷调度时长,分析其最优交易时间。
考虑优化模型中存在大量离散变量,优化变量TTI和报价Q取值仅为整数,同时优化变量范围不大,故采用连续修改参数法[22]计算不同TTI的C,从而确定TTI最优值,如图3所示。
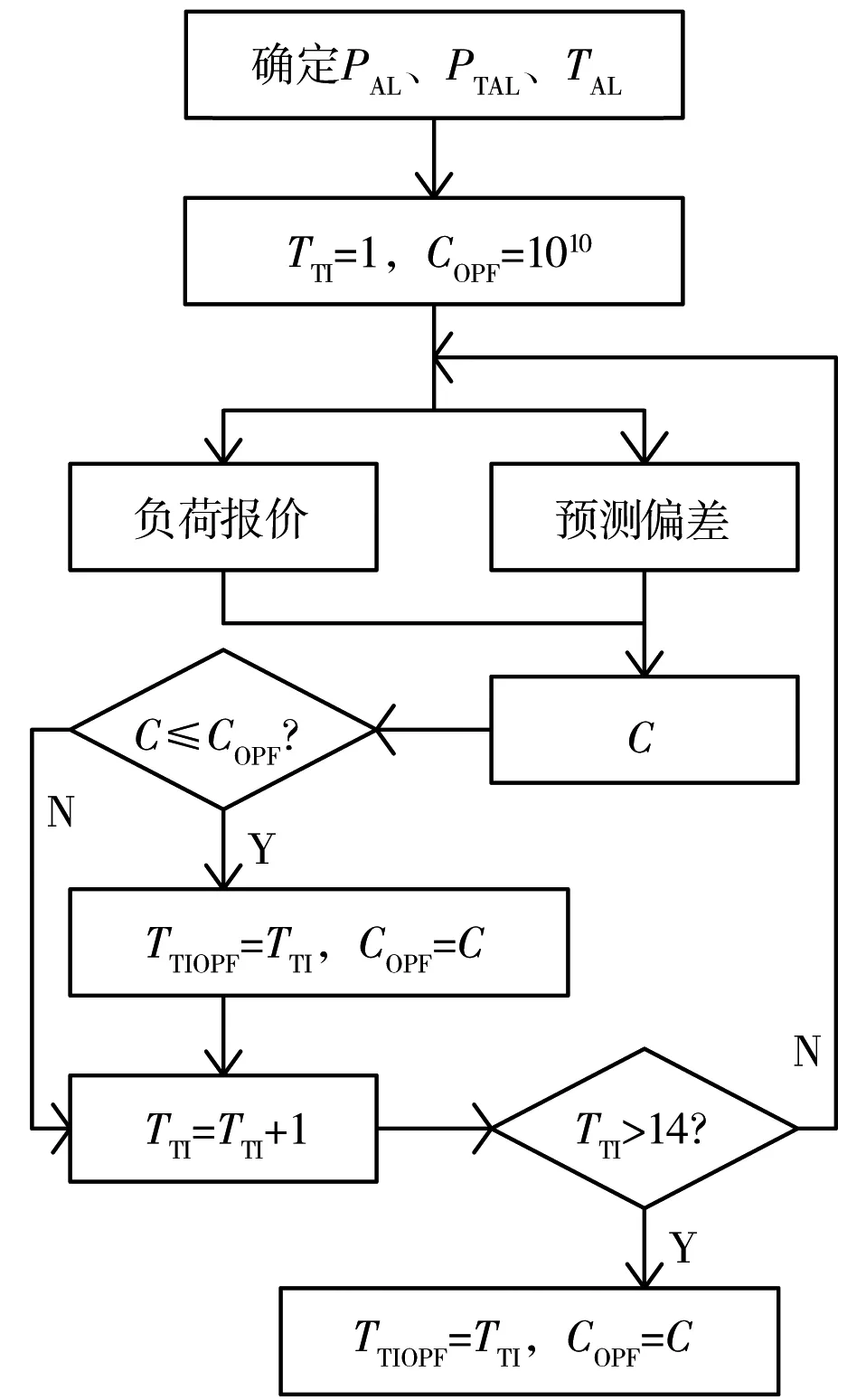
图3 优化算法的计算流程
3 算例分析
3.1 预测精度与预期交易时间的关系
由于不易获取各类型负荷具体数据,故算例以某地区的统一负荷计算分析,验证所提模型。根据某地区2021年1月1日至5月28日负荷数据[23],以工作日为例,取不同交易时间间隔,计算负荷预测偏差平均值见表1。

表1 负荷预测偏差平均值
综合考虑拟合的准确性、复杂度,选用二元多项式描述负荷预测偏差和预期交易时间关系,解得a0=67.41,a1=7.13,a2=1.63。图4给出了实际偏差曲线和拟合偏差曲线,验证了以二元多项式拟合的正确性和可行性。
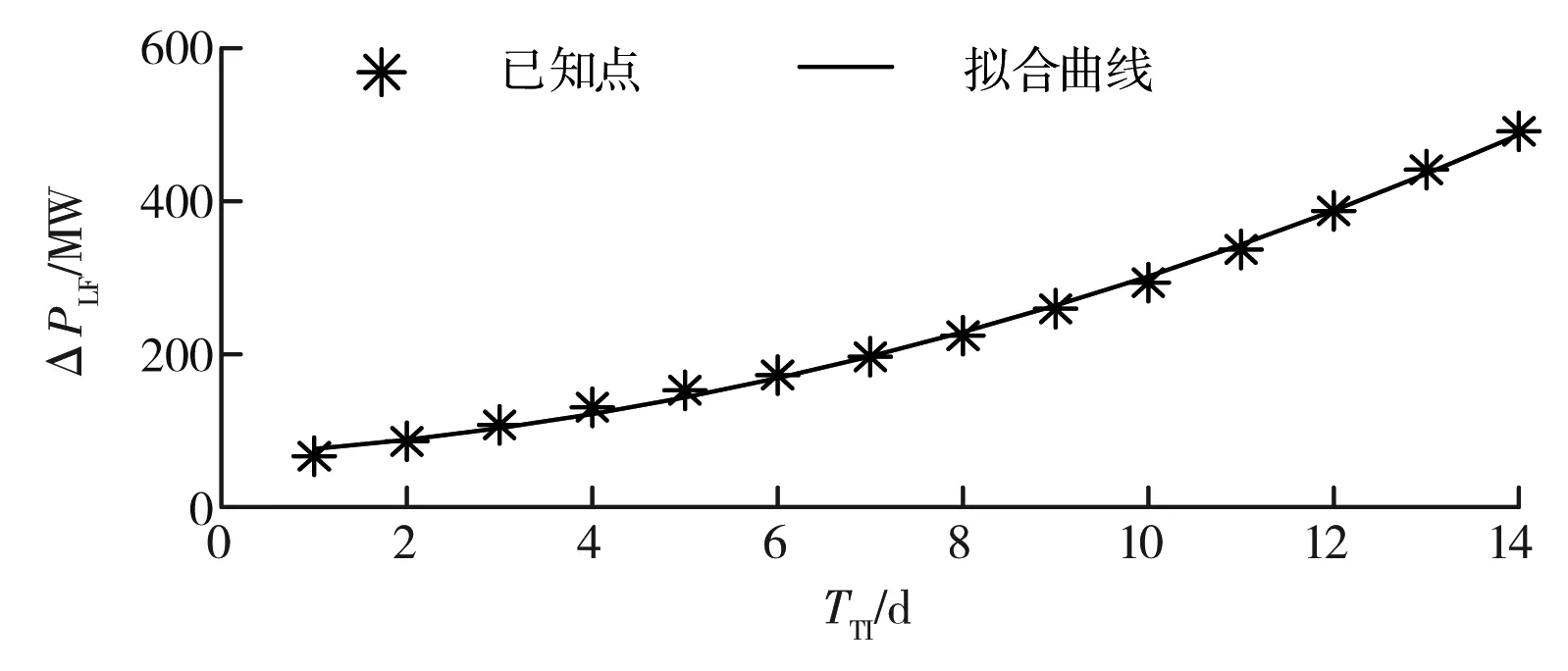
图4 不同预期交易时间的负荷预测偏差
3.2 预期交易时间优化模型
取可调负荷定价参数见表2[16-17,20]。在实际应用中,可根据具体场景修改参数,所提方法仍然有效。
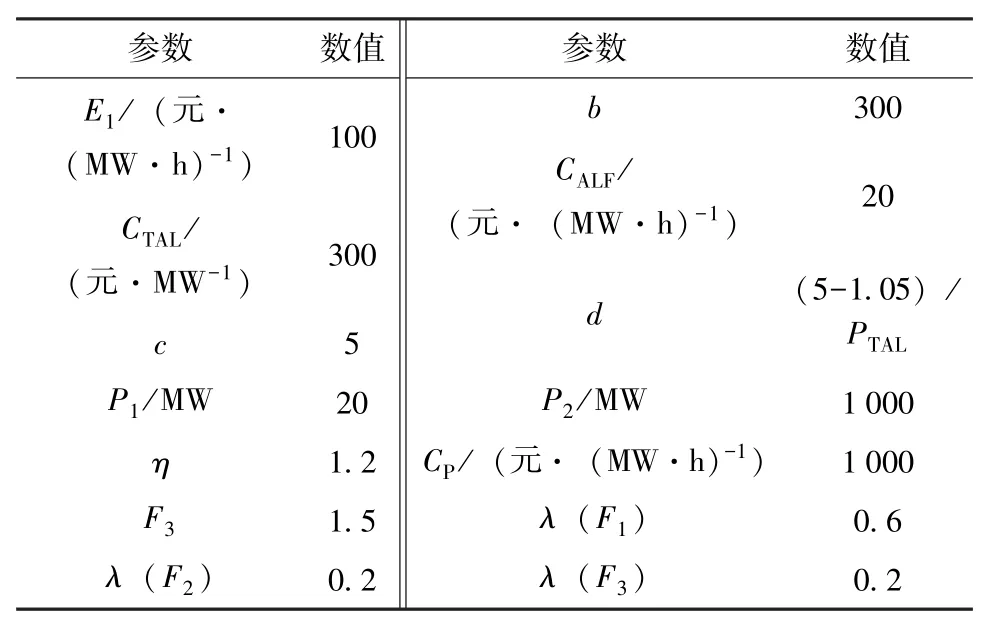
表2 定价策略的参数
取PTAL=1 500 MW,PALF=800 MW,TAL=2 d。当交易时间间隔变化时,售电公司总成本如图5所示。当最优交易时间间隔为5 d时,售电公司总成本为200.93万元,达到最小值。图中最优值左侧灵敏度比右侧更大,即相较偏差惩罚价格,负荷调节成本随预期交易时间变化对售电公司总成本的影响更大。

图5 不同预期交易时间的售电公司总成本
分析负荷调节量、用户可调负荷容量以及可调负荷调度时长影响,取以下三种情况:①PTAL=1 500 MW,TAL=2 d固定,PALF变化。②PALF=300 MW,TAL=2 d固定,PTAL变化。③PTAL=1 500 MW,PALF=300 MW固定,TAL变化。售电公司总成本和最优交易时间如图6所示。交易时间最优值、售电公司总成本随着负荷调节量增大而增大;调节量越大,成本增加幅度越大;交易时间最优值、售电公司总成本随可调负荷容量增大而减小。在负荷调节量确定时,优先选取可调负荷容量较大的用户,可减少总成本;当可调负荷调度时长变长,交易时间最优值未发生变化,总成本增加。
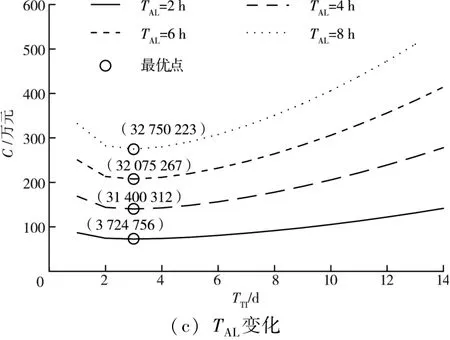
图6 售电公司总成本和最优交易时间

比较发现,负荷调节量对总成本和最优交易时间影响最大,调度时长对总成本的影响相较可调负荷容量更大,但可调负荷容量对最优交易时间影响相较调度时长更大。调度时长对最优交易时间影响较小,可忽略。在调节电量确定时,为减小售电公司总成本,可优先选取小负荷调节量、长调度时间用户,同时相应最优交易时间缩短。
4 结论
本文基于分解预测模型,建立负荷预测偏差和预期交易时间关系,提出可调负荷定价策略。考虑预测偏差惩罚,计算售电公司总成本最小为目标的最优交易时间。得到以下结论:
1)相较偏差惩罚价格,可调负荷调度成本随预期交易时间变化对售电公司总成本影响更大。用户负荷调节量对售电公司总成本和最优交易时间影响最大,可调负荷调度时长对最优交易时间影响最小。
2)售电公司与用户最优交易时间随用户负荷调节量增大而增大,随可调负荷容量增大而减小。售电公司总成本随用户负荷调节量或调度时长变长而增加,随可调负荷容量增大而减少。
3)负荷调节电量确定时,为减小售电公司总成本,可优先选取小负荷调节量、长调度时间的用户,同时缩短对应的最优交易时间。

