一种基于变骨架参数的孔隙度预测新方法
申 波,王 刚,樊海涛,张金风,李彦普
(1.长江大学油气资源与勘探技术教育部重点实验室,湖北武汉 430010;2.长江大学地球物理与石油资源学院,湖北武汉 430010;3.中国石油新疆油田分公司勘探开发研究院,新疆克拉玛依 834000;4.中国石油新疆油田分公司吉庆油田作业区,新疆吉木萨尔 8317002;5.中国石油大港油田分公司第一采油厂,天津 300280)
孔隙度是储层评价中的基础参数,应用测井资料计算储层的孔隙度是测井定量评价技术中最成熟和最基础的组成部分,也是渗透率、含油饱和度等其他储层参数测井评价顺利开展的基础[1-13]。岩心刻度方法是目前最常用的一种计算孔隙度的方法,该方法是通过岩心分析孔隙度与孔隙度测井值进行函数回归建立孔隙度预测模型,此方法将同种岩性骨架参数视为固定值。当地层岩性相同,且岩石矿物组合比例稳定无明显变化时,该方法得到的孔隙度预测效果较好,能够满足储量计算的要求。同时,该方法也依赖于所取岩心的数量是否具有统计意义及岩心分析结果的可靠性。但在实际地层中,岩石往往是由多种矿物组分构成,即使相同岩性的地层也是由特定的几种岩石组分按照不同比例组合而成。因此从理论上讲,利用变化的骨架参数值计算孔隙度更符合储层实际情况。本文旨在针对这类复杂地层提供一种快速有效的岩石骨架参数提取技术,通过孔隙度预测精度分析检验骨架参数提取效果,进而为后续储层测井评价提供可靠保障。
1 岩心刻度测井方法
以A凹陷L组为例,L组自下而上分为L1段和L2段,储层岩性为凝灰质砂岩。根据薄片鉴定结果,其砂质成分复杂多样,主要由凝灰岩、流纹岩等火山碎屑岩及酸性火山岩组成,并存在以硅化和碳酸盐化作用为主的多种蚀变作用,同时伴生次生石英、方解石等多种蚀变矿物。根据孔隙度测井值与岩心分析孔隙度(CPOR)关系图可知(图1),密度(DEN)、中子测井值(CNL)与岩心分析孔隙度相关性较差,显示出多矿物组分造成的测井响应不敏感问题。声波时差(AC)与岩心分析孔隙度关系相对较好,但需要分层位建模以提高孔隙度模型预测精度。根据声波时差与岩心分析孔隙度交会图,L1段与L2段骨架声波时差值存在明显差异,其中L1段高声速岩石组分含量更多,骨架声波时差更小。
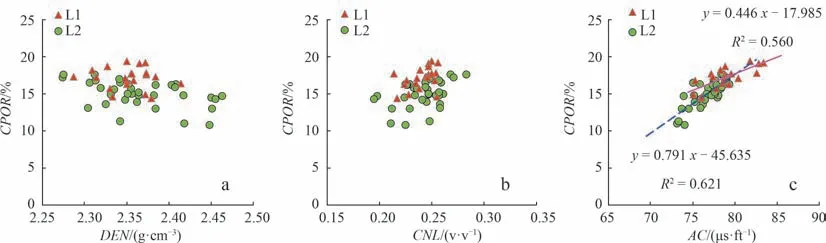
图1 A凹陷L组不同层位孔隙度测井数据与岩心分析孔隙度交会图Fig.1 Crossplotsof porosity valuesfromcore analysis vs.different logging data,L Formation,A Sag
2 变骨架参数提取技术
2.1 主成分分析
主成分分析是由Hotelling提出的一种根据主成分特征值进行降维的数据处理方法[14]。该方法是将多维数据信息矩阵映射到低维空间中,以较少的几个主成分因子表征研究对象多参数信息的综合特征,其中,主成分个数的选取一般按照累积方差大于等于85%或特征值大于1的原则。主成分分析方法的优点在于它是对研究对象所有属性信息进行重组、降噪以提取最具表征能力的主成分因子,而不是对原始变量个数进行取舍和选择。
主成分分析注重目标信息贡献影响力的综合响应,在岩性识别、流体性质识别和储层分类等评价方面均取得了良好的应用效果[15-24]。需要指出的是,只应用综合主成分分析开展研究可能会破坏样本在空间中的相对位置,无法显示原始样本间的差异性,导致所提取的信息重叠、混淆[25],因此需要对提取的主成分进行多维数据的相关性分析,以明确不同主成分的解释意义。
2.2 变骨架参数提取方法
M-N交会图法是综合应用中子、密度和声波时差3种孔隙度测井值进行岩性测井识别的方法,因此也被称为岩性孔隙度交会图。M和N是弱化孔隙度和流体性质的影响,突出岩石组分骨架差异的孔隙度测井组合参数。以N值为例(图2),其本质是在中子-密度交会图中骨架点与水点连线的斜率,反映某一类岩性或矿物在密度测井响应单位增量影响下中子测井值的变化差异,斜率不同则表示岩石组分存在一定差异,而骨架点和水点是在极限条件下(φ=0和φ=100%)的不同矿物组分的测井响应值[26]。M和N表达式为:
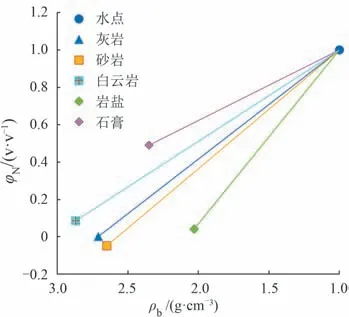
图2 不同岩性和矿物中子与密度测井值交会图Fig.2 Neutron vs.density cross plot of different lithology and minerals
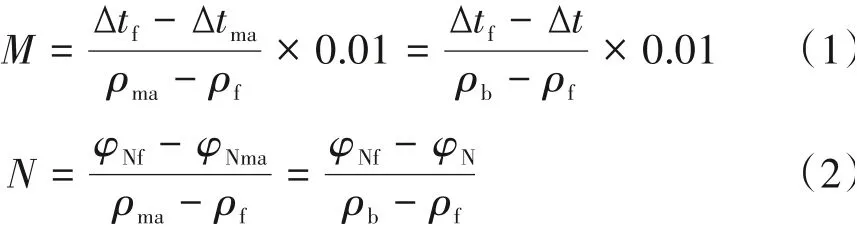
式中:M和N为骨架的组合参数(小数);ρma、φNma和Δtma分别为骨架密度(g∕cm3)、骨架中子测井值(小数)和骨架声波时差(μs∕ft);ρb,φN和Δt分别为密度(g∕cm3)、中子(小数)和声波时差(μs∕ft)测井值;ρf,φNf和Δtf分别为水点的密度(g∕cm3)、中子(小数)和声波时差(μs∕ft)测井值,取值分别为1 g∕cm3、1和189μs∕ft。
M和N值本质上是以斜率的直观方式,反映单位密度变化量对应的声波时差和中子响应特征。定义两者的比值为P,该值则是声波时差与中子测井值之间的联动性,即单位声波时差变化量下中子测井值响应的变化规律。M-N交会图多用于岩性识别、流体性质识别等定性解释,储层定量评价方面很少用到,而基于P值的测井定量评价则更为少见。该参数表达式为:
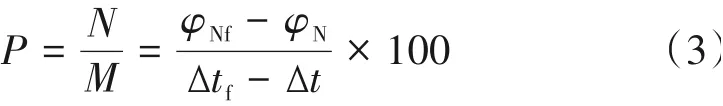
式中:P为骨架组合参数N和M的比值(小数)。
由于M,N和P值为三孔隙度测井不同的组合参数,尽管在一定程度上减弱了孔隙度带来的影响,但三者之间难免会出现骨架信息的重叠以及无效信息的干扰,因此需要消除数据共线性问题,进一步提高数据的信噪比。
将主要岩石组分骨架参数M,N和P值作为主成分分析样本集合,在归一化处理的基础上,通过主成分分析结果检验降维的效果,从而得到所有样本的分布特征;最后根据骨架参数与主成分值相关性建立变骨架参数的预测模型,经过插值即可得到目的层连续变化的变骨架参数值。根据镜下薄片的鉴定结果,先通过砂岩、碳酸盐岩和火山岩骨架参数计算获取M,N和P值,再与L组基于测井数据计算的M,N和P值共同作为主成分分析的原始输入变量。表1为A凹陷L组主要岩石组分骨架参数统计表,其中骨架参数是以薄片资料为依据,根据孔隙度预测效果调整而确定的。
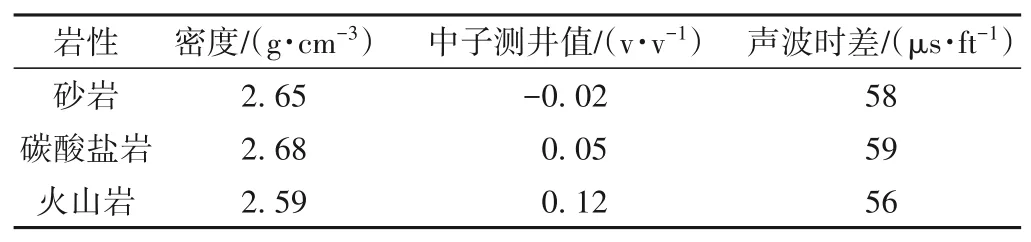
表1 A凹陷L组主要岩石组分骨架参数统计Table 1 The main rock components statistics,L Formation,A Sag
表2为A凹陷L组主成分分析统计。据表可知,提取的两个主成分参数F1和F2的累积方差达到99.985%,表明主成分提取达到了很好的降维效果,可通过主成分F1和F2表征岩石骨架参数特征。根据表2可知,F1与M,N和P均存在较好的相关性,而F2则主要为N和P值的综合响应。
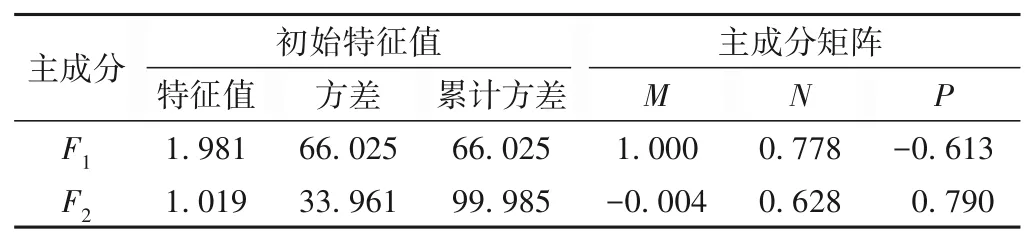
表2 A凹陷L组主成分分析统计Table 2 Statistics of the principal component analysis results,L Formation,A Sag
图3和图4分别为L组凝灰质砂岩储层骨架中子与骨架密度参数预测模型,根据地层连续的F1和F2值,就能得到沿井深剖面连续变化的骨架参数。
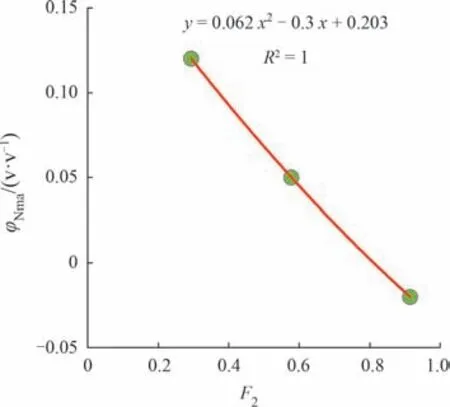
图3 A凹陷L组骨架中子测井值与F2值交会图Fig.3 Crossplot of skeleton neutron vs.F2 values,L Formaton,A Sag
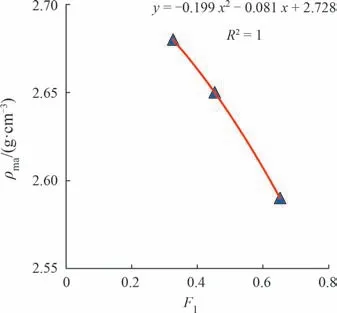
图4 A凹陷L组骨架密度与F1值交会图Fig.4 Crossplot of skeleton density vs.F1 values,L Formation,A Sag
3 孔隙度模型确定
在根据F1和F2得到岩石骨架密度值和骨架中子值的基础上,根据公式(4)和公式(5)计算凝灰质砂岩总孔隙度,为了进一步减小由于泥质和流体因素对孔隙度计算带来的误差,选择公式(6)作为最终的孔隙度预测模型[27]。
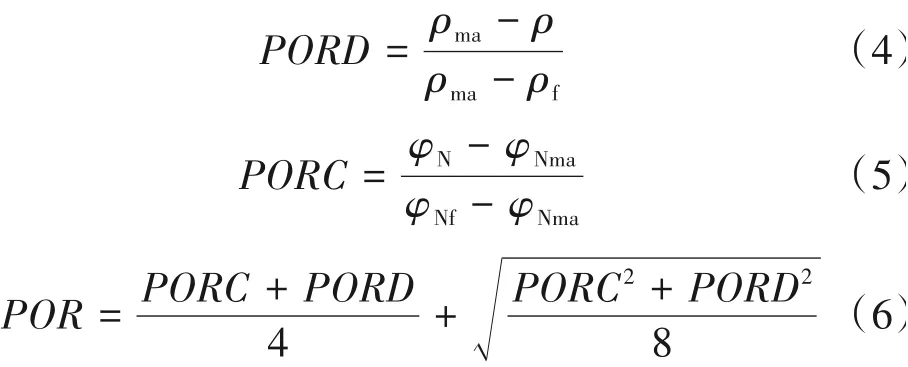
式中:PORD和PORC分别为应用连续变化的骨架密度与骨架中子测井值预测的孔隙度,%;POR为基于变骨架参数最终得出的孔隙度预测值,%。
4 应用效果分析
图5为J1井L组L2段凝灰质砂岩储层孔隙度计算效果对比图。其中POR_AC为根据声波时差测井数据,应用岩心刻度方法得到的孔隙度预测值;POR_MS为应用多元统计方法计算的孔隙度;POR_PCA为应用主成分分析提取骨架参数后,进而应用体积物理模型计算的孔隙度。基于声波时差测井数据的岩心刻度方法预测结果在真实反映地层孔隙发育状况存在一定适应性问题,部分储层预测值明显高于岩心分析值,同时也存在预测值偏低的情况(图5绿色阴影显示,预测值与实测值偏差趋势不同)。利用多元统计方法得到的孔隙度低于实验分析结果(黄色阴影显示),这是由于除声波时差外其他相关性低的孔隙度测井数据引入带来的误差累积效应造成的。
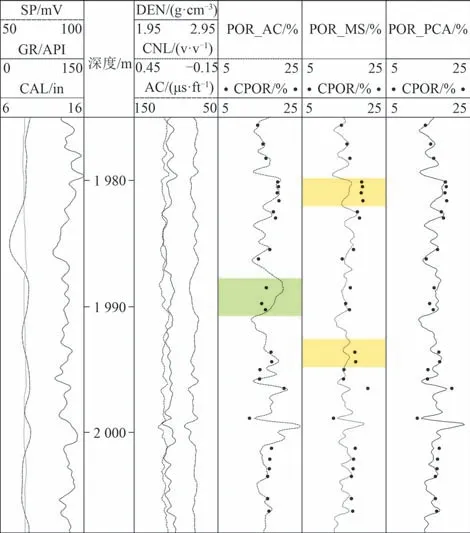
图5 A凹陷J1井L组L2段凝灰质砂岩储层孔隙度计算效果对比Fig.5 Porosity comparison chart for tuffaceous sand reservoir in the 2nd member of L Formation,A Sag(Well J1)
图6为J1井L组L1段凝灰质砂岩储层孔隙度计算效果对比图。与L1段预测结果相同,声波时差模型预测值明显高于或低于岩心分析孔隙度,而多元统计模型预测结果低于岩心分析孔隙度。基于主成分分析方法提取变骨架参数的孔隙度预测值与岩心分析值(CPOR)的平均绝对误差值为0.95%(表3),预测结果精度最高,解决了单因素孔隙度方法数据类型单一的缺陷,也改善了多元统计方法在数据重组时的共线性问题,从而提高了孔隙度测井数据的信噪比,此外该方法还简化了分层位建模的处理流程,能够快速、真实有效地反映地层孔隙发育状况。
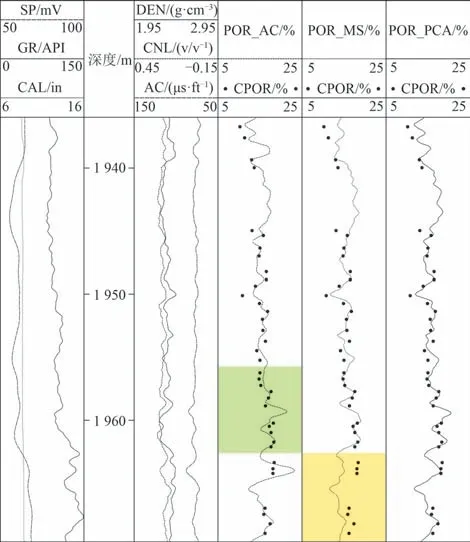
图6 A凹陷J1井L组L1段凝灰质砂岩储层孔隙度计算效果对比Fig.6 Porosity comparison chart for tuffaceoussandstone reservoir in the 1st member of L Formation,A Sag(Well J1)
5 结论
在基本掌握储层主要岩石组分或矿物组合类型的前提下,可以通过主成分分析的降维技术确定岩石骨架的测井组合参数,进而建立变骨架参数的预测模型。在此基础上,应用中子孔隙度和密度孔隙度的综合解释模型,可以进一步消除岩石组分和流体差异对孔隙度预测的影响。实际资料处理表明,将该方法应用于凝灰质砂岩储层孔隙度计算中,预测值与岩心分析值具有较好的一致性。该方法考虑了多种测井信息响应,抑制了无关信息的干扰,降低了误差的引入,同时简化了分层位建模的流程,对于复杂岩石组分地层的孔隙度预测具有一定的借鉴意义。

