基于模板和KNN算法的能量分析攻击对比研究

靳济方，刘承远，范晓红，段晓毅，刘嘉瑜

（北京电子科技学院电子与通信工程系，北京 100070）

0 引言

随着移动通信过程中对信息安全需求的提高，通信终端设备通常采用加密的安全芯片（如手机SIM卡等）保证用户身份认证信息的硬件安全。但随着技术的发展，密码芯片的安全性面临着威胁，其中最大的威胁来自功耗分析攻击。它通过采集密码芯片工作时的能量迹，利用统计分析等手段猜测密码算法的密钥，对终端密码设备的安全构成了极大的威胁。

1999年，Paul和Joshua等[1]提出了差分能量分析（differential power analysis，DPA）恢复DES（data encryption standard）的密钥。2003年，Chari等[2]通过采集大量能量迹样本建立统计信息，利用模板攻击（template attack，TA）获取密钥。2004年，Rechberger和Oswald对模板攻击方法的实际问题进行讨论，并分析了特征点数量对攻击成功率的影响，提出使用差分能量分析攻击寻找特征点的方法[4]。2006年，Archambeau等[5]提出从侧信道信息中选取特征点构成样本的主子空间（principal subspace），以减少模板攻击的运算量。2011年，Gabrielet等[8]首次将机器学习技术应用到侧信道攻击中，利用具有明显汉明重量泄露的数据集进行功率分析攻击，利用最小二乘支持向量机（LS-SVM）成功攻击了一些高级加密标准（advanced encryption standard，AES）的软件实现。2013年，Lerman等[9]提出一种半监督的模板攻击方法，这一方法放松了模板攻击中必须完全掌握被攻击设备的限制。可见，模板攻击和基于机器学习的KNN算法的能量分析攻击日益成为能量分析攻击具有威胁的攻击手段。2019年，Kim等[10]介绍了一种使用卷积神经网络分析侧通道的方法。马向亮[11]使用基于能量分析技术分析芯片后门指令，Ryad等[12]使用CNN攻击了有掩码、扰乱防御的基于单片机上的算法实现，文献[13]利用CNN对单片机上的算法实现进行了掩码和抗干扰攻击。2020年，Cai等[14]提出了差分功率分析攻击的能量曲线压缩方法，段晓毅等[15]使用数据增强技术解决了机器学习中SBOX（substitution box）输出值的汉明重量不平衡问题。

本文对基于TA和KNN算法的能量分析攻击进行了对比研究。在对皮尔逊相关系数（Pearson correlation coefficient，PCC）、互信息和最大信息系数（maximal information coefficient，MIC）、距离相关系数（distance correlation coefficient，dcorr）3种降维方法研究的基础上，选出适合两种能量分析攻击的特征点，进一步研究特征点数量p对两种能量分析方法的攻击成功率以及3种降维方法对两种能量分析方法的攻击成功率的影响等。

1 能量分析攻击

1.1 基于模板的能量分析攻击

TA过程主要可以分为两个阶段：第一阶段为建立模板阶段，第二阶段为模板匹配阶段。最常用的模板攻击模型是多元高斯模型。

其中，建立模板阶段，构建的模板实际是一个二元组T=，由同一时刻该点的电压均值t和计算不同点的协方差矩阵C组成。分为如下3步。

第一步：对L位密钥的2L种可能密钥进行建模。

第二步：每一种可能密钥对同一个明文进行m次加密，得到m条能量/电磁曲线，然后在每条曲线上寻找n个与密钥相关的特征点。计算这n个点的平均值，得到t，如式（1）所示。

第三步：计算不同点的协方差。协方差是构建不同点的相关性，如式（2）所示。

模板匹配阶段是利用极大似然法则，计算能量迹t与模板匹配的概率，概率最大的是匹配最好的模板，对应的密钥是最可能的正确密钥。其概率计算式如式（3）所示。

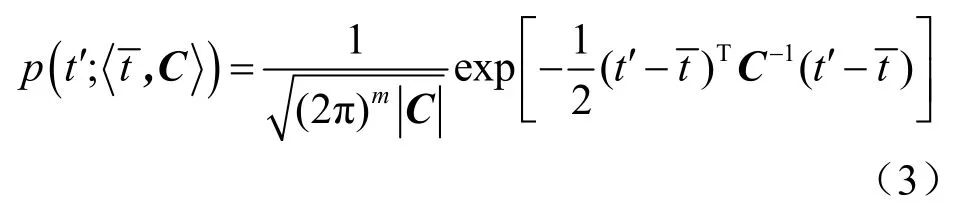
1.2 基于KNN算法的能量分析攻击

KNN作为监督学习中一种分类算法，该算法的中心思想为：若某样本在特征空间中的k个最近邻样本多数属于某一个类别，则该样本属于这个类别。KNN算法原理如图1所示。

图1 算法原理

KNN算法的完整步骤如下：

· 计算测试数据与各个训练数据之间的距离；

· 按照距离的递增关系进行排序；

· 选取距离最小的k个点；

· 确定前k个点所在类别的出现频率；

· 返回前k个点中出现频率最高的类别作为测试数据的预测分类。

其中，k值的选择对训练模型的拟合效果至关重要。k值过大或过小会造成训练模型过拟合或欠拟合。因此，为了解决这个问题，一开始可以先选择一个较小的k值，然后再使用交叉验证的方法最终得到一个适合模型的终值。

KNN在各类开发库中应用广泛。Python3.8 Scikit-Learn机器学习库中的KNN算法函数是此类库函数中一个经典的例子。本文中，该函数输入为测试集功耗曲线以及对应的类标签（即AES-256算法的字节代替环节第一个SBOX输出汉明重量值），输出则为具有分类功能的模型（函数默认近邻数量k=5，距离默认欧氏距离p=2）。再将测试集功耗曲线给到该模型进行分类预测。在测试过程中，最后需要将上述得到的汉明重量值与测试集数据实际对应的标签值进行对比，以得到基于KNN算法进行能量分析攻击时的攻击成功率。

2 降维技术的原理及实现

进行能量分析攻击的第一步是将庞杂的能量数据进行降维，去除噪声，将攻击对象（密钥等敏感数据）有关的点保留，即进行特征点选择。

2.1 特征点选择

目前使用机器学习应用于能量分析攻击是能量分析攻击的一个研究热点，而特征点选择是影响机器学习模型的一个重要因素，当输入数据的特征点数较大时，数据的冗余会造成训练结果差；当输入数据特征点数较小时，小的特征子集不能满足训练算法的需求，从而引起过拟合现象，导致模型误差变大。因此，攻击者在进行模板攻击前，会对功耗曲线上的特征点进行筛选，选出与关键数据相关性高的点，把区分度不够的点排除，以此提高输入数据的优质程度。要评估相关性，需要引入统计学中的概念和统计量衡量。本文将分别使用3种常用的特征点选择方法：PCC、MIC和Dcorr对输入数据进行优化。

2.2 3种降维技术原理

2.2.1 皮尔逊相关系数

PCC是实现分析特征以及响应变量间关系的一种方法，其实现简单且计算效率较高，能有效衡量各个变量间的线性相关性，结果的取值区间为[−1，1]，−1表示完全的负相关，1表示完全的正相关，0表示没有线性相关。

PCC计算式如式（4）所示。

其中，X、Y是变量的值，N为样本数。

2.2.2 互信息和最大信息系数

一般来说，互信息（MI）是指随机变量X与Y在计算时产生的交互信息，其中用I(X;Y)表示各个事件间互信息，如式（5）所示。

可以通过分析互信息检测定性因变量与自变量间的相关性。但互信息在应用于特征选择时具有一定的缺陷。若计算一组连续的变量，就必须先将变量离散化，但将变量离散处理，互信息的结果就会受到一定影响，出现计算误差。

MIC解决了互信息存在的以上缺陷。其在离散化变量之前挑选一个最优方案，再将互信息的取值方式变为统一化的标准度量方法，如式（6）所示。

将取值区间定在[0,1]，相较于互信息而言，MIC有更高的准确度。

2.2.3 距离相关系数

传统的PCC存在一定的缺陷，在实际计算过程中，即使PCC的值为0，也不能证明计算变量是相互独立的。但距离相关系数有效克服了这一缺点，当计算的距离相关系为0时，可以完全证明两个计算变量是相互独立的。距离相关系数是基于距离的变量u、v间相对独立性的研究，其可以表示为ˆdcorr(u,v)，如式（7）所示。当ˆdcorr(u,v)为0时，则证明两变量是相互独立的；ˆdcorr(u,v)的值越大，则证明两个变量间的相关性越强。

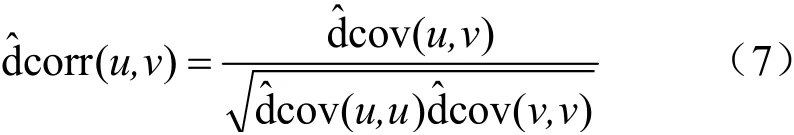
3 实验结果与分析

本实验将差分功耗分析（differential power analysis，DPA）国际学术大赛第四阶段（DPA contest v4）[16]的数据集作为实验对象，该数据集包含10 000条能量曲线，每条能量曲线包含435 000个特征值，本文实验攻击点为S盒输出，模型为汉明重量模型。对TA和基于KNN算法的能量攻击性能进行对比研究。

3.1 特征点选择

本文实验选用的数据集包含10 000条能量曲线，每条能量迹对应的时刻点是相同的，为了提高实验运算速度，本文仅选择前r条（r= 100、200、300、400）能量曲线分别采用3种降维技术实现特征点选择。

3.1.1 PCC进行特征点选择

使用PCC进行特征点选择时，X为一组能量曲线，Y为这组能量曲线对应的S盒输出的汉明重量值，把X和Y代入式（4），得到曲线中与Y相关性较大的特征点（绝对值越接近1的点），选择这些特征点进行能量分析攻击。不同r值计算出435 001个特征点对应的PCC如图2所示。

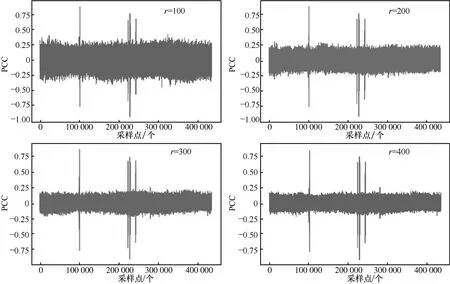
图2 不同r值计算435 001个特征点对应的PCC

3.1.2 MIC进行特征点选择

使用MIC进行特征点选择时，X为一组能量曲线，Y为这组能量曲线对应的第一个S盒输出的汉明重量值，把X和Y代入式（6）中，即可以得到曲线中与Y相关性较大的特征点，选择这些特征点进行能量分析攻击。不同r值计算出435 001个特征点对应的MIC如图3所示。

3.1.3 Dcorr特征点选择

使用Dcorr进行特征点选择时，u为一组能量曲线，v为这组能量曲线对应的第一个S盒输出的汉明重量值，把u和v代入式（7），即可以得到曲线中与v相关性较大的特征点，选择这些特征点进行能量分析攻击。不同r值计算出435 001个特征点对应的Dcorr相关系数如图4所示。

图4 不同r值计算435 001个特征点对应的Dcorr相关系数

由图2、图3和图4可知，3种特征点选择方法均适用于能量分析攻击，均可以很好地选择特征点。且不同的能量曲线条数对相关系数的结果是有影响的，可以看出当能量曲线条数r=300、r=400时的图像已经趋于相同，所以在统筹节约运算时间和效果的前提下，暂选定r=300。

3.2 特征点数量p对攻击成功率的影响

3.2.1 特征点数量p对TA的影响

对于TA来说，每条功耗曲线选取特征点p不能过多。每个模板中的功耗曲线是对相同操作数的多次测量，所以具体功耗值都是十分接近的，当选取的特征点越多时，对应的协方差方阵C规模越大，矩阵的行列式越接近于0，即被看作一个奇异矩阵，没有逆矩阵。在模板匹配时采用多元高斯分布概率密度公式中需要用到协方差矩阵的逆矩阵−1C，所以在TA的过程中每条曲线选取的特征点个数不能太多。经过实际测试，特征点个数p不能大于27。采用300条能量曲线（r=300），基于PCC技术进行特征点选择后，对数据进行p值分析。p值的选择对基于TA的能量分析攻击成功率影响如图5所示。

图5 p值的选择对基于TA的能量分析攻击成功率的影响

由图5可知，特征点个数p值对基于TA的能量分析攻击的影响较为明显。整体上看，当p值越大时，基于模板的能量分析攻击成功率越高（少数情况有小幅波动）。当p≤23时，攻击成功率在0.85以下，相对较低；当p≥24时，攻击成功率提高到0.86~0.87；当p= 27时，攻击成功率最高，达到0.868以上。

3.2.2 特征点数量V对KNN算法的影响

采用300条能量曲线（r=300），PCC进行特征点选择后得到的数据进行p值分析。p值的选择对于基于KNN算法的能量分析攻击成功率影响如图6所示。

图6 p值的选择对基于KNN算法的能量分析攻击成功率的影响（k=7）

由图6可知，当p值逐渐增大，攻击成功率逐渐升高（少数情况有小幅波动），当p值超过某阈值后，攻击成功率转而逐渐降低。当p=50时，攻击成功率最高，达到0.928。

3.3.3 特征点数量p对两种能量分析攻击的横向比较

由图5和图6可以看出，当p∈[20,27]时，两种能量分析攻击方法的攻击成功率均很高，将p与两种能量分析攻击方法进行横向比较，分析p值的选择对两种能量分析算法的影响。p值的选择对两种能量分析攻击方法的影响如图7所示，整体上看，基于KNN算法的能量分析攻击成功率明显高于基于能量分析攻击成功率，其平均成功率之差在0.066 7以上。

图7 p值的选择对两种能量分析攻击方法的影响

综上可得，针对PCC降维技术得到的数据集，当两个模型选取相同个数的特征点p时，明显看出结果基于KNN算法的能量分析攻击成功率更高，且p值的改变引起攻击成功率的波动幅度更小，即基于KNN算法的能量分析攻击的鲁棒性更强。

3.3 不同特征点选择方法对攻击成功率的影响

本节将分析PCC、MIC和Dcorr 3种特征点选择方法对模板攻击和KNN算法攻击成功率的影响。

3.3.1 能量曲线条数固定的影响

当能量曲线条数r为300时，经过3种特征点选择方法得到数据集，对两种能量分析攻击方法的攻击成功率见表1。TA表示基于模板的能量分析攻击，KNN表示基于KNN算法的能量分析攻击，特征点个数p为27。

表1 3种特征点选择方法对两种能量分析攻击成功率的影响（r=300）

由表1可知，PCC、MIC和Dcorr 3种特征点选择方法对两种能量分析攻击方法的影响程度不同，其中，对基于TA的能量分析攻击的整体影响范围在0.04内，对于基于KNN算法的能量分析攻击的整体影响范围在0.02以内。其中，MIC特征点选择方法对两种能量分析攻击方法的成功率更高。

3.3.2 不同能量曲线条数的影响

控制变量保持不变：特征点个数p=27，KNN算法中近邻数量k=7。分别对比经3种特征点选择方法得到的数据对两种能量分析攻击成功率的影响。其中，r值的选择对PCC降维技术效果的影响如图8所示，r值的选择对MIC降维技术效果的影响如图9所示，r值的选择对Dcorr降维技术效果的影响如图10所示。

图8 r值的选择对于PCC降维技术效果的影响

图9 r值的选择对于MIC降维技术效果的影响

图10 r值的选择对于Dcorr降维技术效果的影响

由图8可看出，对PCC降维技术来说并非在计算相关系数时选择的功耗曲线的条数越多越好，在r=50时，两种能量分析攻击的成功率最高。具体地，对基于高斯模板的能量分析攻击来说，在r=300时攻击成功率优于除r=50的其他情况，基于KNN算法的能量分析攻击来说，r值在大于50之后攻击成功率没有很大波动，基本趋于稳定。

由图9可看出，对MIC降维技术来说计算相关系数时选择的功耗曲线条数越多越好，另外由曲线的波动幅度可以看出基于高斯模板的能量分析攻击对r值的改变反应更为敏感，而当r≥300后，攻击成功率没有很大的波动，基本趋于稳定。

由图10可看出，对于Dcorr降维技术来说，当r≤300时，r值的增大会导致两种能量分析攻击成功率的降低；当r=200时，两种能量分析攻击成功率最低；当r≥250后，攻击成功率在一个较小的范围内变化（成功率不如r=50时高），没有很大的波动，基本趋于稳定。

综上可以得出，为达到较理想的能量分析攻击效果，采用不同降维技术，应选择不同功耗曲线条数计算相关系数，即选择不同的r值。对于采用PCC降维技术，r=50时，两种能量分析攻击的成功率最高，效果最理想；对于采用MIC降维技术，r=300或r=400时，两种能量分析攻击的成功率最高，效果最理想；对于采用Dcorr降维技术，r=50时，两种能量分析攻击的成功率最高，效果最理想。

3.4 两种能量分析攻击方法比较

由第3.3节可以看出，攻击成功率方面，KNN算法的攻击成功率和鲁棒性明显优于模板攻击，从运算速度和内存使用情况看，基于模板的能量分析攻击训练模型的速度较快，内存使用空间较小，而基于KNN算法的能量分析攻击训练模型的运算速度较慢，内存使用空间较大。原因是KNN算法属于机器学习算法，模型训练时需要耗费大量内存空间完成计算。两种能量分析攻击在攻击成功率、鲁棒性、运行速度和占用内存4个方面的对比见表2。

表2 两种能量分析攻击方法的对比

4 结束语

通过本文的对比研究，基于PCC、MIC和Dcorr的3种特征点选择方法均适用于能量分析攻击，均可以很好地选择特征点；特征点p的数量对两种攻击方法的攻击成功率都有一定的影响。不同的降维技术对模板攻击和基于KNN算法的攻击成功率有区别。MIC特征点选择方法对两种能量分析攻击方法的成功率更高；为达到较理想的能量分析攻击效果，建议采用不同的降维技术时，应选择不同条功耗曲线计算相关系数。采用PCC降维技术时，r值选择50，可使两种能量分析攻击的成功率最高；采用MIC降维技术时，r值选择300或400，可使两种能量分析攻击的成功率最高；采用Dcorr降维技术时，r值选择50，可使两种能量分析攻击的成功率最高。

本文主要针对传统的模板分析攻击和KNN算法的攻击进行对比研究，实验结果表明模板攻击在运行速度、占用内存优于基于KNN算法的攻击，而在攻击成功率和鲁棒性方面，基于KNN算法的攻击具有更好的表现。当然，有很多方面仍可做进一步的研究和完善：进一步优化KNN算法，使其在运行速度、占用内存方面得到提升；采用多种特征点选择方法来对两种攻击方法进行探索。