川中秋林地区致密砂岩水平井多簇射孔优化设计方法及应用效果

唐波涛，曾冀，陈伟华，陈一鑫，王涛，刘成，冯逢

（1.中国石油西南油气田公司工程技术研究院，四川成都 610017；2.中国石油西南油气田公司勘探事业部，四川成都 610041；3.中国石油西南油气田公司致密油气勘探开发项目部，四川成都 610051）

近年来，致密气藏的勘探开发逐渐受到人们的关注[1]，合理的分段分簇是确保致密气水平井压裂效果的前提。常用方法是依据油藏数值模拟，再结合随钻测井及录井综合解释结果，确保产能最优来进行压裂段及射孔簇的划分，但分段及分簇射孔位置选择是否具备工程条件上的可压性，或者能否通过压裂改造，使各簇裂缝都能正常延伸，提高裂缝复杂度，仍未考虑[2−5]。因此，提出了一种基于地质和工程双因素的综合分段分簇优化方法，考虑了分段布缝位置诱导应力干扰、渗流阴影对压裂效果的影响。

1 地质特点及改造难点

秋林地区沙溪庙组致密砂岩气藏资源丰富，是川渝油气开采的重要新区块。该地区处于中江和八角场之间（工区东面为八角场、西面为中江），为三角洲河道砂体沉积。储层表现出低孔低渗、窄河道的特点，天然裂缝欠发育，脆性指数低，非均质性极强，总体特征与八角场比较接近。前期借鉴EOG 公司在八角场区块沙溪庙组的“密切割、高密度完井”等工艺，在秋林地区沙溪庙组8 号砂体进行了应用（图1）。试验结果表明：该压裂工艺能显著提升改造效果，提高水平井单井产量。但目前的改造目标大多以均匀密切割提单产为主，对非均质性较强的河道砂岩分段分簇目标还尚不明确，其经济有效的工艺参数还有待优化。

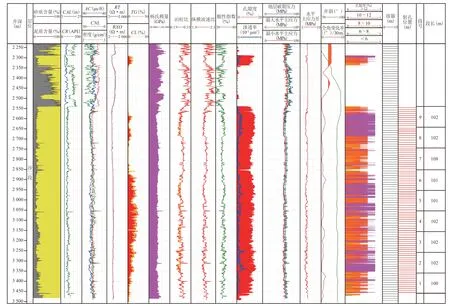
图1 川中秋林地区H井试验密切割改造Fig.1 Tight cutting transformation of test of Well-H in Qiulin of middle Sichuan

2 水平井多簇射孔优化设计方法

2.1 河道砂岩水平井有效渗流边界模型

2.1.1 秋林地区裂缝形态

通过前期取心证实秋林地区沙溪庙组砂岩储层天然裂缝欠发育，储层脆性指数低的客观事实，并通过大量物模实验（施工制度：上覆应力20 MPa、水平最大应力25 MPa、水平最小应力17 MPa、排量恒流35 mL/min）表明，无天然裂缝影响的砂岩试样，仅能形成一条将试样一分为二的贯穿缝（图2），因此，秋林地区压裂裂缝形态主要以双翼缝为主。

图2 砂岩压后裂缝形态及裂缝重构形态Fig.2 Fracture morphology and fracture reconstruction of sandstone after fracturing

压裂施工结束后，在每条双翼缝周围会形成一定范围的水力裂缝可控线性渗流压力边界，该区边界线内以线性渗流为主，相较于改造前井筒径向渗流，大大提高了地层流体的产出效率[6]。但水力裂缝可控线性渗流压力边界并不是无限大，即远离水力裂缝一定距离的地层流体仍然难以参与线性渗流，需要在井筒方向进行加密改造[7]。

裂缝可控线性渗流压力边界一定程度上决定于合理的布缝方式（图3a）。布缝密度过高则会产生图3b所示的过度改造，浪费成本；若布缝密度过低则会产生图3c所示的储层改造不足[8−10]。因此，计算线性渗流压力边界是优化布缝密度的关键，裂缝周围任一点（x，y）处的孔隙压力随时间变化式为：

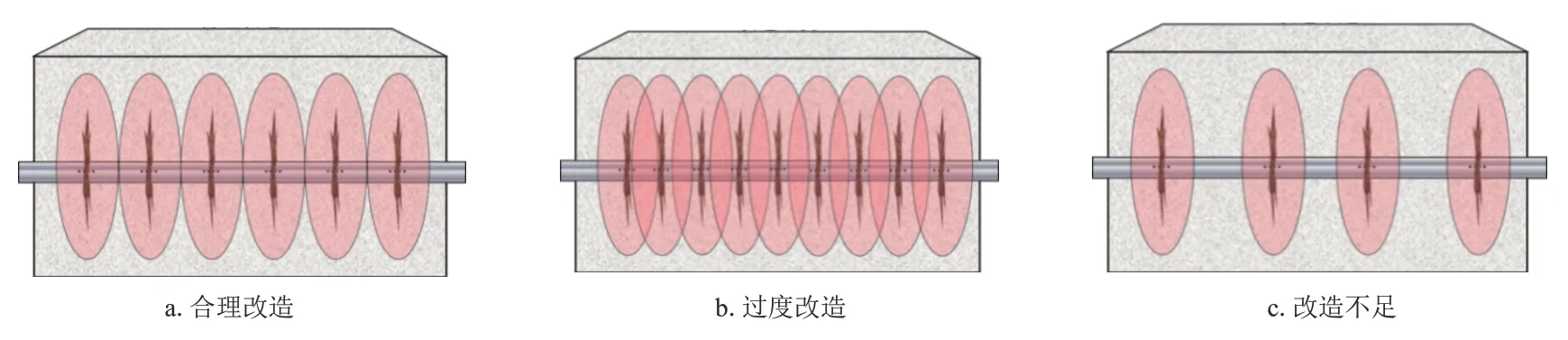
图3 三种不同改造布缝密度下的线性渗流压力边界分布Fig.3 Linear seepage pressure boundary distribution under three different reconstruction joint densities

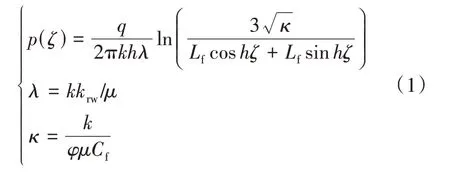
式中：p为孔隙压力，MPa；q为通过压力边界的地层流体流量，m3/min；λ为地层流体流度，10−3µm2/（mPa·s）；k为地层渗透率，10−3µm2；μ为地层流体黏度，mPa·s；Cf为裂缝压缩系数；φ为孔隙度，%；h为裂缝高度，m；krw为液体相对渗透率；κ为裂缝中流体流度，10−3µm2/（mPa·s）；ζ为多孔介质单位体积液体体积的变化[11−14]。

2.1.2 水力裂缝线性渗流场模型

在水力压裂过程中，压裂液从裂缝面滤失到地层中引起裂缝附近压力增加，孔隙压力的变化将影响水力裂缝周围的应力分布[15]。设裂缝半长为Lf，裂缝高度为h，在椭圆坐标系中（图4），裂缝周围的点（x，y）可以表示：

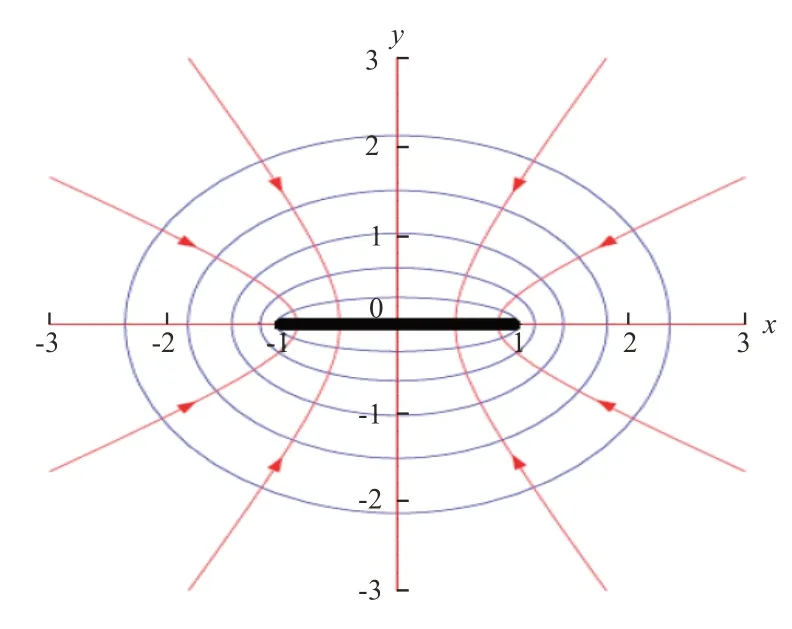
图4 椭圆坐标系Fig.4 Schematic diagram of elliptic coordinate system

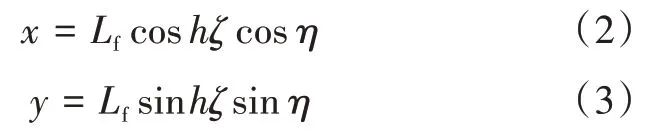
式（2）—（3）中：x为线性渗流压力边界垂直井筒方向的距离，m；y为线性渗流压力边界沿井筒方向的距离，m；Lf为裂缝半长，m；η为导压系数，m2/s。

根据AREIAS P 等的研究成果，裂缝周围任一点（x，y）处的孔隙压力随时间变化的数学表达式为：

式中：pi为原始地层压力，MPa。

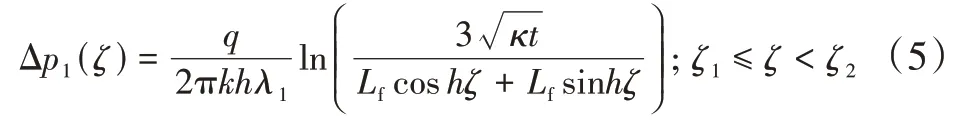
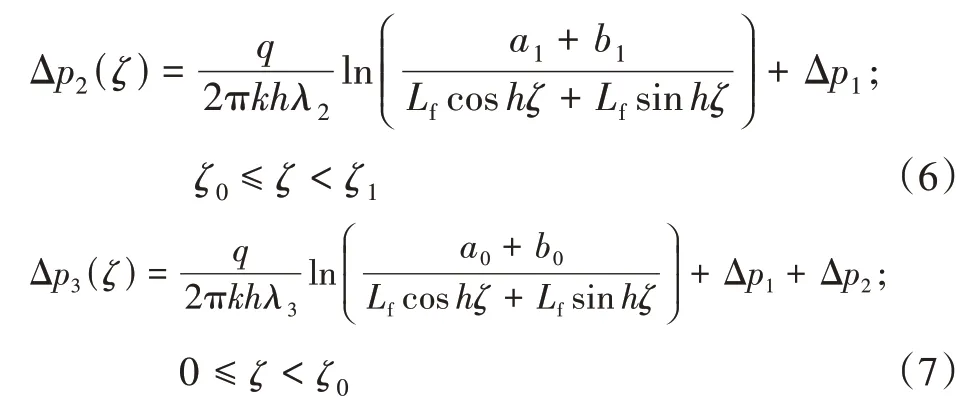
2.2 基于裂缝干扰的多缝延伸应力耦合模型

裂缝在扩展过程中会改变原始地应力场，新的应力场会对之后各级裂缝形态造成影响，这一概念称为“应力阴影”效应[16]（图5）。因此，对水平井进行射孔分段压裂设计时，必须考虑应力阴影的影响[9,17−18]。

图5 裂缝间的相互影响Fig.5 Interaction between fractures

假设地层为无限大地层，井眼半径rw，外边界半径re，地层为均质油藏、渗透率k各向同性；内外边界定压，在外边界处压力pe。则扩散方程：

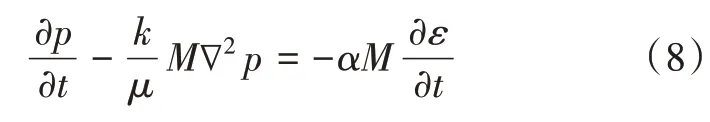
压力—应变关系式：

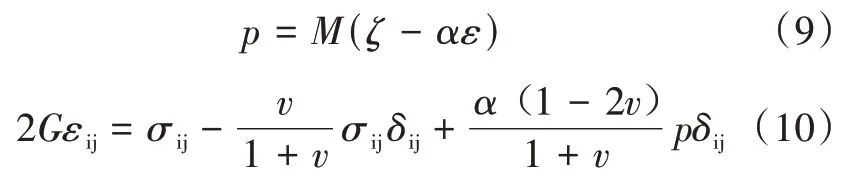
式中：εij为应变张量，m；σij为应力张量，MPa；v为泊松比；δij为克罗内克符号。

根据应力平衡方程、协调方程、连续性方程，利用拉氏变换，结合初始条件和边界条件，最终可以得到钻井成孔诱导应力场、注入流体渗流诱导应力场、初次裂缝延伸诱导应力场等三场叠加的总应力场：

孔隙压力：

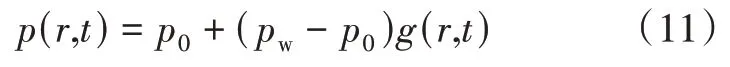
径向应力：

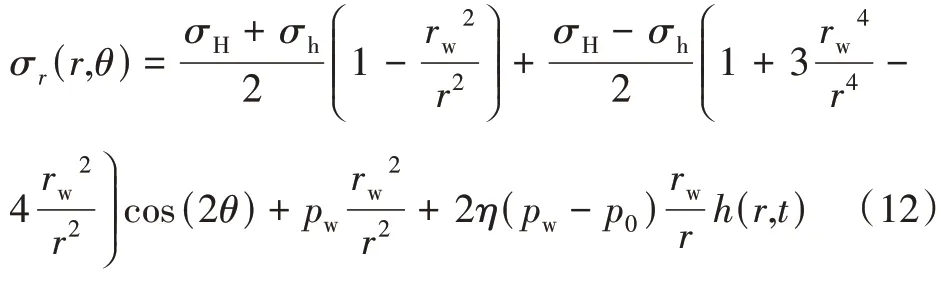
切向应力：

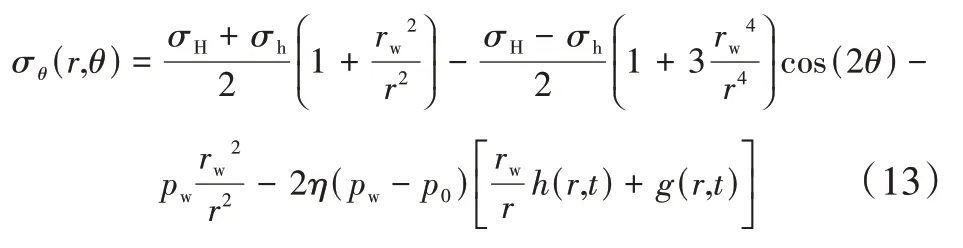
剪切应力：

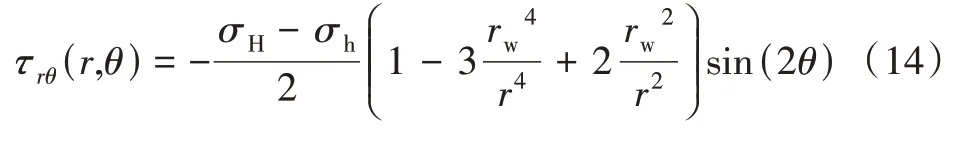
2.3 水平井多簇射孔优化设计

2.3.1 簇间距下限

合理优化簇间距是经济有效动用致密油气藏的关键环节[19]，簇间距下限根据2.2 节建立的多裂缝诱导应力场模型，对上述相关方程进行离散化求解，分别计算得到了100 m 井段长度下不同簇间距的理论裂缝形态，计算结果如图6所示。

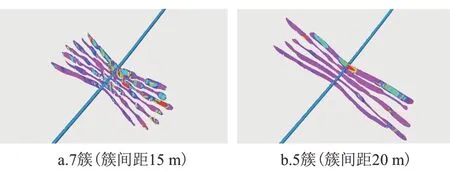
图6 不同簇数、簇间距裂缝形态Fig.6 The fractures morphology of different clusters

对上述不同簇间距下的裂缝长度数据进行提取，如图7所示，可以看出，当簇间距减少到一定程度（间距12 簇/7 m）之后，段内的缝长开始出现显著差异，表明缝间干扰效应明显；在簇间距保持5 m 不变的情况下，受缝间干扰，多簇裂缝半长为0 m。因此，界定簇间距最低不宜小于7 m。

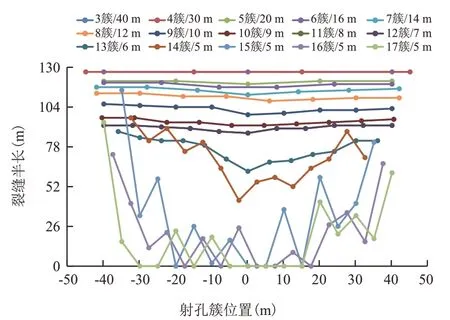
图7 各射孔簇间距对应缝长的对比Fig.7 Comparison of fracture length corresponding to perforation cluster spacing

2.3.2 簇间距上限

在确定最小簇间距的基础上还要避免出现对储层的过度改造，因此，还需要确定簇间距的合理上限，保证每条裂缝形成的压降漏斗不至于分散隔离。根据有效渗流边界理论计算多裂缝的叠加压降场，并进行数值求解，得到不同簇间距下渗流场的计算结果如图8所示。

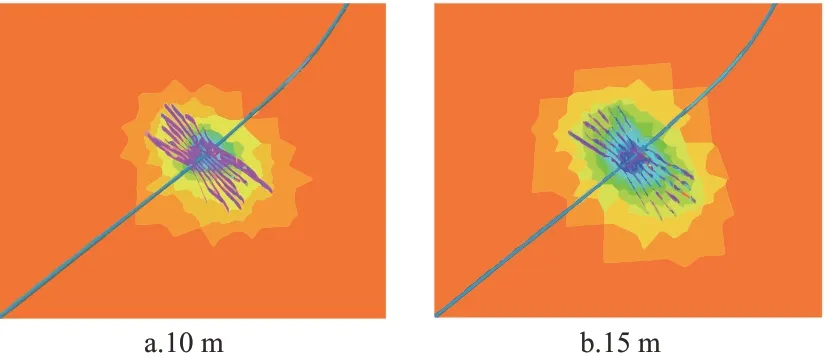
图8 不同簇间距裂缝压降叠加场Fig.8 Pressure drop superposition field of fractures with different cluster spacing

将上述计算结果的压降漏斗进行数值提取并绘制在同一坐标系中对比，如图9所示。

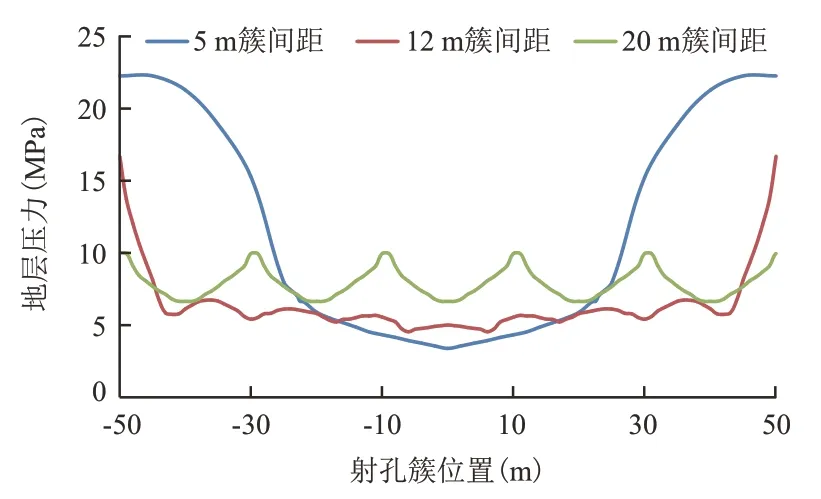
图9 不同射孔簇间距下的压降漏斗数据提取曲线Fig.9 Pressure drop funnel data extraction curve under different perforation cluster spacing

从图9可以看出，当簇间距为5 m 时，压降场最小值最低，是因为多条裂缝压降场均在中央部位形成叠加。当簇间距增大到12 m 时，各条裂缝激活的压降场彼此相接并且整体保持在较均一的数值。当裂缝间距增大到20 m时，出现压降场的分离。通过以上分析，确定秋林地区裂缝间距上限不宜超过12 m。

2.3.3 综合分簇优化射孔

以川中河道砂岩致密气井轨迹通过的储层特征、岩石矿物组成、自然伽马、全烃显示为基础划分合理的试油段。在地质试油段内结合段内各处的含气显示、储层物性、力学性质、固井质量这4个因素进行综合压裂精细分段，原则上将储层性质相似的划为一段。划分压裂段后，结合前面有效应力场边界模型、诱导应力场模型确定最优簇间距范围，再根据岩石破裂压力剖面，在合理簇间距范围内选择破裂压力处于较低位且相差不大的位置进行射孔。

2.4 现场应用

根据Q井的储层、岩石力学等基本参数，对该井水平段分簇射孔优化设计，优化簇间距整体为7～10 m，微地震监测裂缝延伸状态良好，平均延伸长度约为369 m（图10）。射孔簇开启率92.3%，指导该区块井均测试产量由2020年的17.66×104m3/d 提升至37.53×104m3/d（图11、图12）。

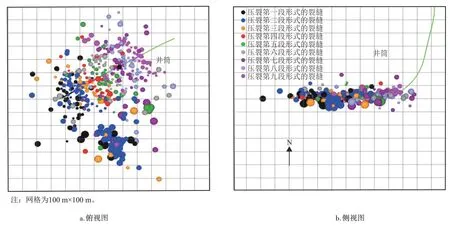
图10 秋林地区Q井地面微地震监测整体效果Fig.10 Overall effect of surface micro-seismic monitoring of Well-Q in Qiulin area

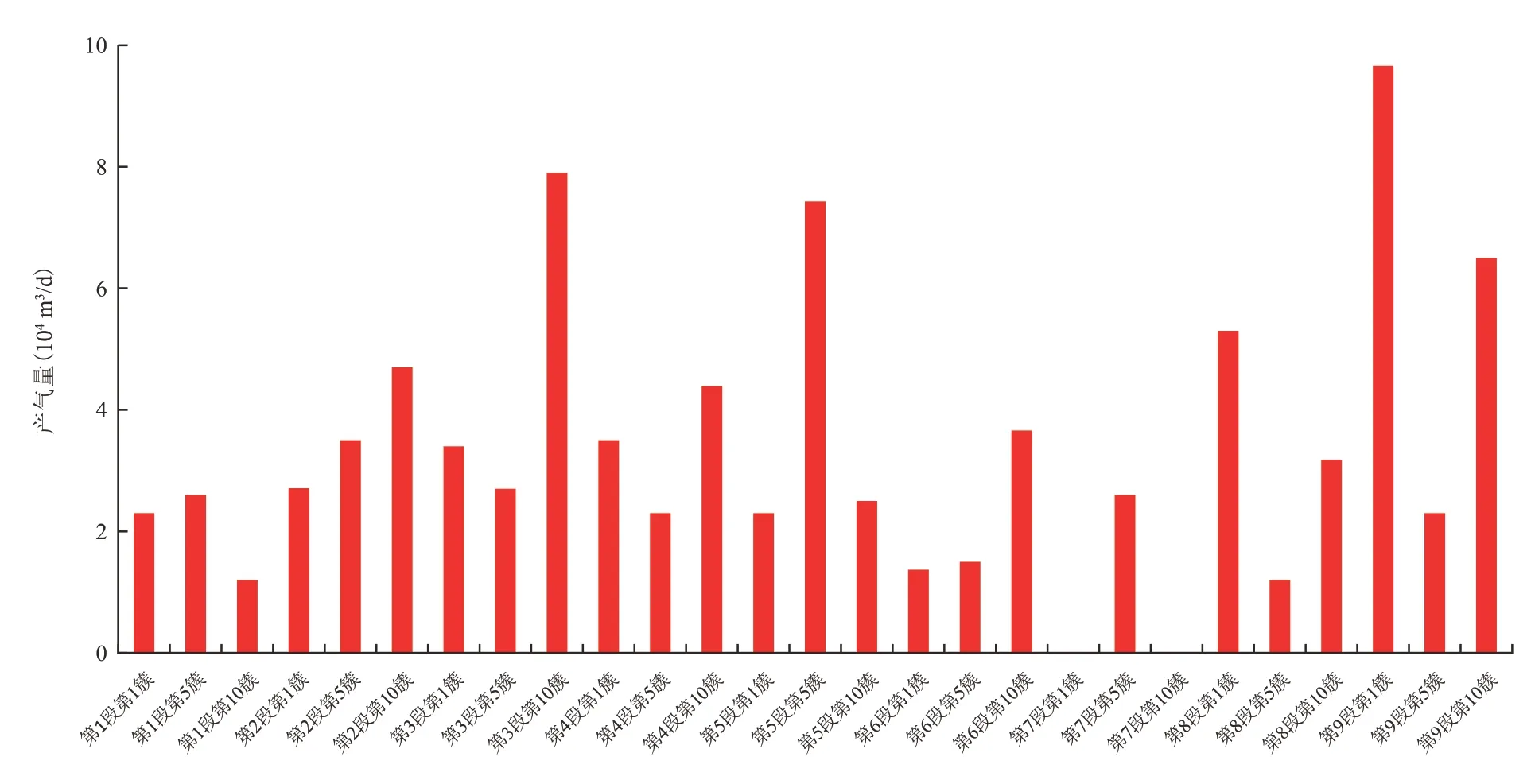
图11 秋林地区Q井各簇生产测井产气量贡献Fig.11 Logging of contribution of cluster production of Well-Q to gas production in Qiulin area

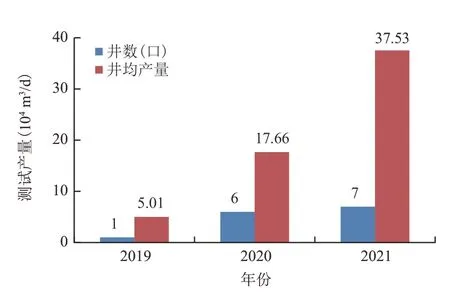
图12 秋林地区致密气测试产量对比Fig.12 Comparison of production of tight gas testing in Qiulin area

3 结论

1）经过大物模实验研究发现，天然裂缝欠发育的秋林区块致密砂岩储层，主要形成“双翼缝”，难以构造缝网，因此，将改造思路转变为通过增加段内射孔簇的方法形成多条人工主缝，人为提升裂缝复杂程度，提出了以多簇缝为主体形态的压裂改造模式。

2）通过对裂缝诱导应力的分析表明，在没有天然裂缝影响下，小簇间距裂缝会相对平行地延伸，但是当缝间距过小会出现裂缝相互抑制的现象，不利于充分改造储层，因此，需要计算能够保证所有裂缝均匀延伸的合适缝间距，为此展开了适用于砂岩的缝间干扰理论模型研究。通过对不同缝间距下裂缝长度的模拟，在秋林区块地应力条件下所有缝长均能得到平稳延伸的缝间距为7～9 m，因此，设计射孔簇分布位置最小值为7 m。

3）通过对裂缝—气藏渗流条件的分析，扩大缝间距不利于裂缝激发渗流场的相互连接，即基质渗流场不能完全覆盖全井段。在通过不同缝间距渗流场的模拟计算后，得出能够保证裂缝激发的合理簇间距上限为12 m，至此确定秋林地区合理簇间距为7～12 m。

4）现场阶段实施验证了理论研究成果的适用性，确立了以“段内多簇射孔+高强度加砂”的主体压裂工艺技术，优化了分簇射孔压裂参数，秋林地区致密气井水平井射孔开启率达到92.3 %以上，指导川中秋林地区致密气产量再提升112%。