基于ST-number 算法的配网GIS 单线图自动生成方法研究

王沈亮，刘 坤，李盛盛，李 莉，程 伟

（南京南瑞信息通信科技有限公司，江苏南京 210000）

随着电网技术的发展，各种信息流和能量流的交互增加了自动成图的难度，且难以实现较高的准确度。传统配电网单线图的绘制主要通过人工进行，人工绘制虽然可控性较强并具有较高的灵活性，但是其效率较低，成图慢且成图风格不统一，可读性不强。通常配网单线图是通过CAD 成图，其绘制过程为离线的方式，无法实现实时更新。而目前的电网经常面临改造和新建，变动频次和规模较大，需要耗费大量精力，且准确性受绘制人员的心理和习惯的影响较大，这给配电网的日常运维检修带来了一定的困难。而维护人员拿到图纸的准确度和易读性在很大程度上决定着事故处理的进度[1-2]。

目前所采用的自动成图算法大多较为单一，存在准确率较差、成图存在交叉等缺点[3]。文中结合单线图传统自动成图技术，加入智能算法，将其应用于单线图的自动成图技术中，并取得了较好的效果。

1 单线图自动成图技术

1.1 技术原理

文中所指单线图即配电网的电气联络图，主要用来表示复杂配电网接线的电气联络关系。随着电网负荷的密度逐渐增大，需求也越来越高，多数用户均要求使用双电源以保证自身用电[4-6]。供电可靠性的要求变高，直接导致了配电网的电气联络关系复杂化。目前，农村或其他负荷密度较低的区域多使用单辐射的接线形式；城市、城镇以及新建园区等区域主要使用联络的接线形式。对于单辐射线路而言，其单线图的自动生成通常不容易出错，可以较为清晰地描述出各个节点的电气联系。但对于联络型接线模式的线路，必须对其联络开关和支线归属准确识别。这种电网密集型发展的模式，要求单线图自动生成技术必须具备更强的适应性、鲁棒性以及准确性[7]。

目前的配电网单线图自动生成技术仍在不断发展，电力和计算机领域的大量学者进行了不断的努力和尝试，取得了一定的成果。针对配电网单线图的正交化、最少交叉、连线尽量短、美观等绘制目标[8]，若利用智能算法进行处理，则不可避免地会涉及到多目标优化问题。

1.2 成图原理及交叉识别

配电网线路通常是依据节点来控制的，比如曼哈顿距离[9]和欧氏距离[10]，以曼哈顿距离为例，线路总长度的曼哈顿距离为：

其中，i、j为两个电气节点的下标；xi、yi为对应的坐标点；δ(i,j)为delta 函数，在图1 所示的单线图中，若两节点之间存在直接电气联系，则该函数值为1，否则为0。

图1 单线图相关距离定义

通常而言，需减少支路之间的交叉，其目标数学模型如下：

判断支路i和j是否交叉，主要通过快速筛选和判断跨越的方法，具体如下：

1）快速筛选，判断两个支路所形成的矩形是否存在重合的面积。但该方法仅能快速、粗略地识别不符合要求的支路。

2）对剩余的无法筛选出是否重合的支路，其判断方法为跨越判别，基本原理为：若两支路存在相交，则必定存在一方跨越另一方的情况。

将上述两步骤所对应的数学模型合并如下：

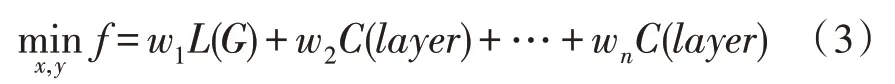
其中，w为对应权值，其对最终结果的影响最大。因此，在进行线路优化时，需要使用遗传算法或粒子群算法等进行求解。

2 算法理论

2.1 图 论

对于配电网的电气联络图，本质上也包含了连线和节点，因此将配电网的单线图划分为点、线、面的组成元素[11-13]。其中，点对应电力系统的电气节点，线对应电力线路，面则对应一个地区或一个高压变电站的供电区域。面是由点与线围绕组合而成的，三者关系的研究是图论的重点。

图论中对平面连通图的定义是可以绘制为无交叉平面图，而非平面连通图。无论如何规划其路径，均存在交叉。其原理如图2、图3 所示。

图2 平面连通

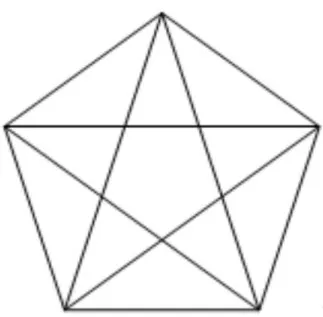
图3 非平面连通

由图2 可见，所谓的平面连通图可以通过调整连接方式，使得在二维平面内实现无交叉连接；而非平面连通图则无法实现无交叉连接。通常平面性判断的方法分为顶点添加法和线路添加法。

2.2 ST-number算法

ST-number 算法原理可通过一个连通图表示[14]。首先将图4 中的每个节点用1～n进行编号，联通完毕后，图4 所示的编号即称为ST-number。

图4 ST-number示例

为更好地发挥ST-number 算法的性能，自上至下依次绘制，得到ST-number的丛形式。图5即为图4的丛形式。

图5 ST-number丛形式表示

2.3 PQ-tree算法

PQ-tree 是由P、Q 节点作为其线路的连接点，其连接按照树状图的方式由上至下进行。其节点类型分为父节点和子节点两种，其中父节点是指其下端有与之相连的枝干；而子节点是指仅有上端的父节点而没有下端子节点的节点。将节点分为这两种的作用是便于计算机进行分类与分析的处理，从而保证出图的准确性[15-16]。

文中的PQ-tree计算机自动成图思路与人工绘制的思路相似。如图6以点来表示P节点，以矩形来表示Q节点，将ST-number生成树与PQ-tree进行对照。

图6 丛形式和计算机PQ-tree

按照上述PQ-tree 的绘制和生成方式，根据原图形是否能够生成平面图分为两种：一种是按照原算法即可直接生成平面图；另一种则需要先生成立体图，再转化为平面图。

3 实现方法

3.1 总体步骤

文中自动成图采用多步骤分解模式进行，主要分为平面化与正交化两个步骤。其主要数据流的流向如图7 所示。

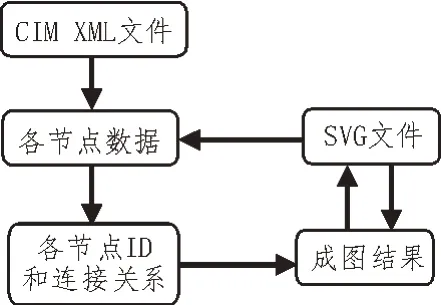
图7 主要数据流流向

如图7 所示，首先是提取CIM XML 文件中的数据，对各节点数据进行分析和预处理。随后针对各节点ID 和其连接关系，生成初始单线图，再与SVG文件相互校对，以此实现对现有电网资料的整理和校核，同时生成准确、可用的单线图。

3.2 平面化处理

平面化处理首先需要计算出ST-number 的个数，根据需要手动选择起点和终点。在此过程中，需要有多个具有实际意义的节点，将这些节点连接起来，则构成了平面图。这种节点在电力系统中一般取变电站的母线，初始起点尽量选择电压等级较高、主变容量大的电气节点。若无法判别，则按照产生随机数的方式定义起点，供电距离最远的点定义为终点。将选定的起点和终点连接，按照ST-number的顺序进行PQ-tree 简化处理。计算完成后，将所有节点按照自下而上进行匹配，最终选择最优的连线拓扑，按照成图质量评判标准进行选择[17-18]。

3.3 正交化处理

正交化处理需要在二维平面上进行，各个点和面均需要确定相互关系。根据相互关系来梳理点和面的逻辑，确定连线，再在各连线中选择最优路径。最优路径的选择应按照点和面的约束条件，在确定初始值的前提下寻找最优正交化方案。整体流程如图8 所示。

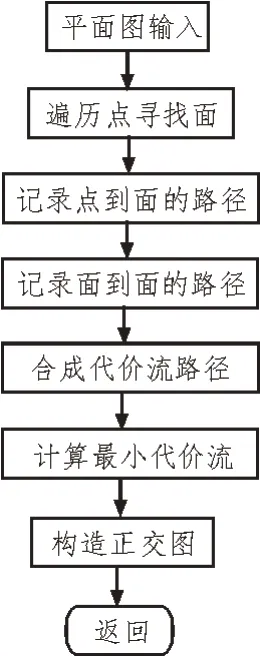
图8 正交化处理流程

4 算例与数值分析

根据文中所述成图方案，对IEEE30 节点系统进行测试。在此基础上，增加配电网复杂程度，选择IEEE118节点的配电网络测试其正交算法的有效性。

同时，将文中算法与粒子群算法相互对比分析。该文粒子群算法的优化指标为节点之间的曼哈顿距离，最小距离且无交叉即为最优路径和方案。粒子群算法成图相关主要参数，如表1 和图9 所示。

图9 迭代次数与交叉数、重叠数的关系

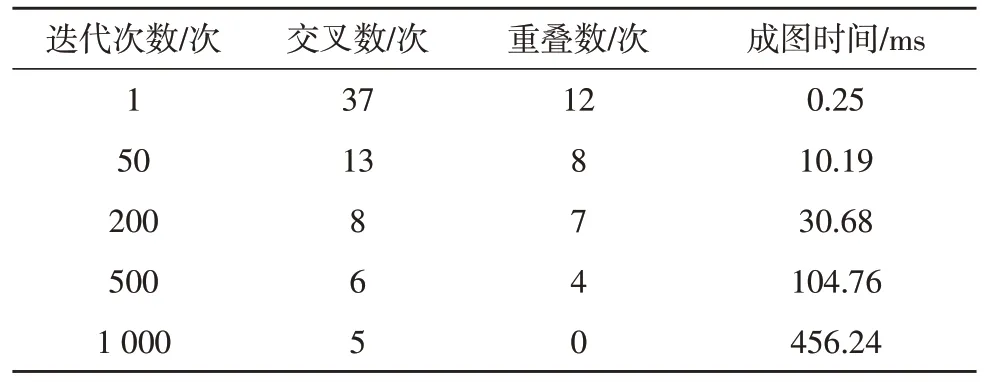
表1 粒子群算法成图相关数据

由上述结果可知，粒子群算法需要多次迭代才能计算得出无交叉或交叉较少的结果，尽管其需要的时间相对较长，但相比人工作图的准确率和效率要高得多。对于文中的多目标分解成图方案，主要数据如表2 所示。

表2 多目标分解成图方案主要指标

由表2 结果可知，该文的多目标分解成图算法不但比人工作图的准确性高，同时与粒子群算法相比较，也表现出了显著的效率优势。由分钟级变成了毫秒级，且交叉数均为0，作图质量与人工相当。

5 结束语

单线图自动绘制在如今和未来的配电网系统中具有重要的意义，其能够代替人工绘制、提升出图效率、增加出图准确度。该文采取数学统计和图论相结合的方式生成单线图，其能够发挥各自的优势，更易于实现实际中所需要达到的目标。最终采用算例完成了该文算法和粒子群算法的出图特征量对比，证明了该文多目标分解成图算法的优越性，既优化了图形绘制的效果，又拓宽了成图技术研究的思路。未来配电网会出现更大规模的电力资产物联，这种软件、硬件相互耦合的系统更需要鲁棒性更强的单线图自动生成技术。另外，风力、太阳能、储能、电动汽车充电站等新元素的出现，也会对单线图自动成图技术带来冲击。因此，应不断改进以适应日益变化的配电网。