基于最小二乘法的隧道地表沉降拟合研究

王润钰， 易 顺， 黄珏皓

(1.武汉华立建设项目管理有限公司， 武汉 430014； 2.中国科学院 武汉岩土力学研究所， 岩土力学 与工程国家重点实验室， 武汉 430071； 3.中国科学院大学 工程科学学院， 北京 100049)

随着中国城镇化加速，亟须开展大量城市地下工程的建设，其中就有大量的城市隧道建设。隧道施工不可避免会造成地层扰动，进而产生不同程度的地表沉降，从而对隧道施工及周围环境的安全产生不利影响。

目前国内外学者对隧道施工引起的地层或地表沉降进行了大量研究，并取得了丰硕的研究成果。徐敬民等[1]研究了地表筏板基础框架结构对隧道施工引起砂质地层移动与变形规律的影响；李钊等[2]以甘肃省某隧道台阶法施工参数优化为例，以上台阶长度和循环开挖进尺为参数，利用三维有限元分析方法开展围岩及支护结构稳定性分析；程红战等[3]和李健斌等[4]研究了考虑参数空间变异性情况下的隧道地表沉降规律；易顺等[5]研究了考虑土体小应变特性的隧道地表及地表变形规律；张云鹏等[6]基于高斯过程回归理论对隧道围岩大变形进行了预测；邓崴等[7]依托广州地铁2号线工程，对砂土黏土互层地层的地表横向沉降规律展开了研究；侯丰等[8]依托温州盾构隧道工程对单线隧道和双线隧道的地表沉降规律展开了研究; 杨福麟等[9]以武汉地铁虎名区间隧道开挖工程为背景，对地表沉降展开了数值模拟研究。Peck[10]在1969年提出一种预测地表沉降的经验公式。由于该公式参数较少，易于理解，因而Peck公式被广泛地应用到隧道工程的案例中[11-12]。但目前国内对双侧壁导坑隧道引起的地表沉降研究仍有不足，利用Peck公式来拟合研究地表沉降规律还相对较少。

基于此，本文依托武汉市红黏土地区光谷一路-高新四路排水通道工程，提出基于最小二乘法的Peck公式拟合方法，并将该方法应用到双侧壁导坑隧道开挖引起的地表沉降研究中，对不同施工阶段的地表沉降展开分析，同时对本文所提出的拟合效果进行研究，从而为后续类似隧道工程的施工建设提供有益的参考。

1 基于最小二乘法的Peck公式回归分析

Peck公式[10]的基本假定是：在不排水情况下，盾构隧道穿越土层所引起的横断面沉降曲线近似符合正态分布曲线，同时土体损失体积等于沉降槽体积。Peck公式的相关公式为

(1)

式中：S(x)为距离隧道中轴线x处的地表沉降，m；Smax为最大地表沉降，m；x为地表到隧道中轴线的距离，m；i为沉降槽宽度系数；Vi为隧道单位长度引起的地层损失，m3/m；φ为隧道周围地层的内摩擦角，(°)；Z为地表到隧道中心的距离，m。

为了更好地利用Peck公式进行回归分析，对上式取对数，可以得到

(2)

基于最小二乘法原理，以lnS(x)和-x2/2为变量进行求解，即以S和x分别代替lnS(x)和-x2/2，同时令a=lnSmax，b=1/x2，则可以得到

S=a+bx

(3)

利用最小二乘法进行回归分析，相当于考虑回归的误差平方和最小，此时得到的拟合效果是最佳的，即

(4)

2 数值模型的建立

武汉红黏土地区光谷一路-高新四路排水通道工程采用双侧壁导坑法进行施工，隧道穿越自稳性较差的红黏土地层。笔者根据实际情况，基于PLAXIS平台建立三维有限元分析模型，由上而下分别为素填土(3.0 m)、红黏土(8.5 m)和强风化硅质岩(28.5 m)，模型尺寸为50 m×20 m×40 m。双侧壁导坑隧道按照实际施工顺序进行分步、分块地开挖。

本文综合考虑目前各本构模型的特性和适用范围，认为红黏土适用于小应变硬化土模型(HSS模型)，因此利用HSS模型来表现红黏土的应力应变行为。数值计算的相关参数通过现场勘察资料、PLAXIS软件手册以及文献资料获取，见表1。同时在隧道开挖过程中，周围锚杆以梅花桩形式分布在隧道周围进行加固，笔者采用刚度等效的方法对锚杆进行模拟。其中，衬砌及临时支撑以及钢拱架经等效后得到的等效厚度和刚度直接赋予板单元中，结构单元参数见表2。另外，图1给出了双侧壁导坑隧道施工到某一阶段，岩体、初次衬砌、二次衬砌和临时支撑的空间位置图。对于整个数值模型，其底部施加竖向位移约束，前、后两侧施加y方向位移约束，左、右两侧面施加x方向位移约束。开展数值计算之前首先对整个模型进行初始地应力平衡。

表1 土体参数

表2 结构参数

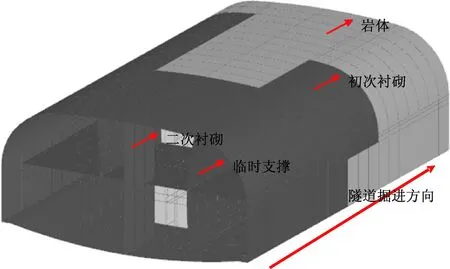
图1 双侧壁导坑隧道掘进至某一开挖阶段时的情况

3 地表沉降分析

在隧道开挖过程中，需要对地表沉降变形进行重点关注。为避免数值模型边界因素的影响，选取隧道掘进方向最中间位置处的横剖面作为研究对象，分析该剖面处的地表沉降随施工过程的变化规律。图2给出不同阶段的剖面地层竖向位移云图，其中以左上导洞和中下导洞进尺情况描述施工进程。从中可以看出，随着隧道的向前推进，地层的沉降变形逐步增大，Peck沉降凹槽范围逐步向外延伸。

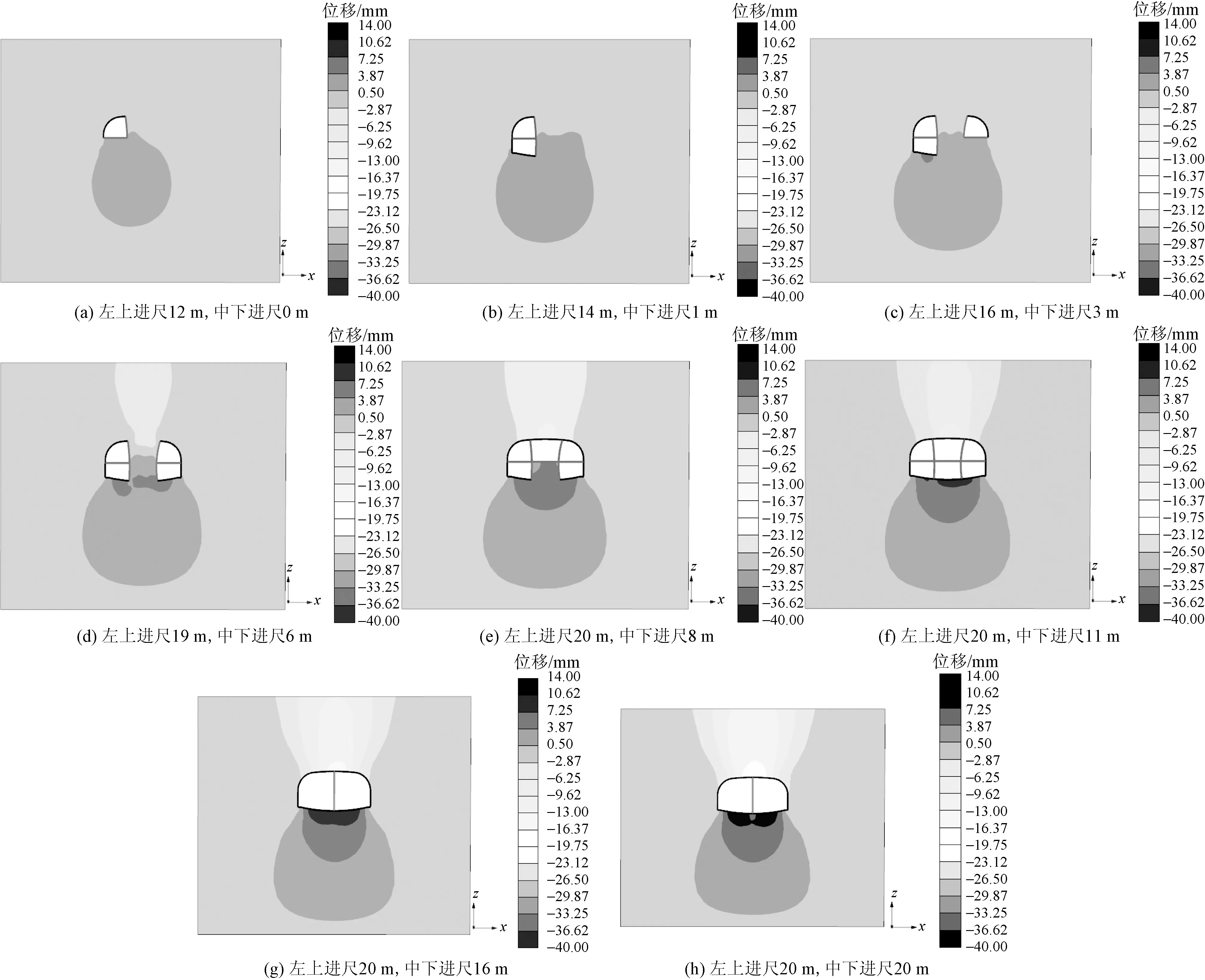
图2 数值模型轴向中央剖面的地层竖向位移云图

在此基础上，提取地表沉降数据，绘制如图3所示的地表横向沉降过程曲线。可以看出随着施工推进，地表沉降最大值逐步增大，隧道施工引起的地层损失也逐渐增大；地表沉降曲线在不同施工阶段都呈Peck沉降曲线分布形式。以此为基础，利用Peck公式对不同施工阶段的地表沉降曲线展开回归分析。

图3 不同施工阶段的地表横向沉降曲线

利用第2节中的回归分析步骤进行分析，图4分别给出左上进尺20 m，中下进尺8 m；左上进尺20 m，中下进尺11 m；左上进尺20 m，中下进尺16 m；左上进尺20 m，中下进尺20 m这4种情况下，地表沉降的拟合回归情况。可以看出，不同施工阶段的地表沉降曲线拟合度都超过98%，说明了基于最小二乘法的回归分析对双侧壁导坑隧道施工引起的地表沉降曲线拟合的正确性。

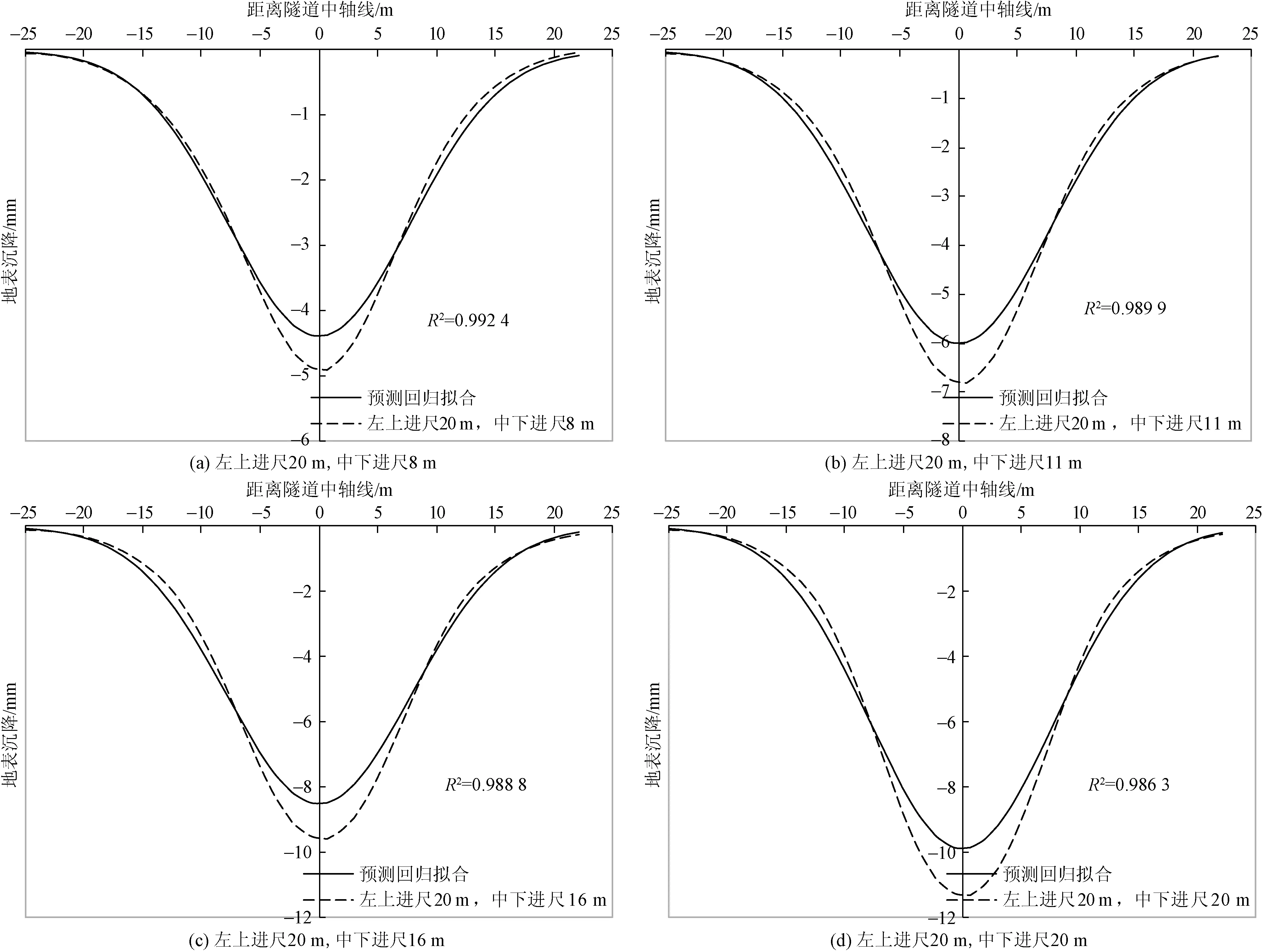
图4 不同施工阶段地表横向沉降曲线的回归分析

4 结论

本文依托武汉红黏土地区光谷一路-高新四路排水通道工程，基于PLAXIS软件平台，对双侧壁导坑隧道施工过程展开数值分析。在此基础上，利用最小二乘法的回归分析方法对不同施工阶段的地表沉降曲线进行拟合，得到以下结论：

1)随着施工推进，地表沉降最大值逐步增大，隧道施工引起的地层损失也逐渐增大；地表沉降曲线在不同施工阶段都呈Peck沉降曲线分布形式。

2)基于最小二乘法对双侧壁导坑隧道施工引起的地表沉降曲线进行拟合是合理的。