“格物致理、慎思笃行”——数学物理方法课程教学改革、创新与实践

祝 俊，李 禄，李志坚，马 杰

(山西大学 物理电子工程学院，山西 太原 030006)

1 课程定位和特点、教学中遇到的问题

数学物理方法[1-3]是既具有数学类型又具有物理类型的二重性课程，课程内容体现了数学与物理的有机融合，既有数学理论深度，又有物理实用性.数学物理方法课程是山西大学物理学专业(国家基地)的专业必修课，在大二上学期开设，5个学分，共80课时，它是前修课程(高等数学)的补充和提升，并为后续专业课程(“四大力学”)的学习奠定数学基础，在物理学本科专业课程体系中起着承上启下的作用.通过本课程的学习，使学生掌握复变函数、积分变换的基本理论，掌握三类典型方程定解问题的常用解法，了解贝塞尔函数及勒让德多项式的概念、性质以及它们在解数学物理方程中的作用，培养学生的逻辑思维能力以及数学建模、求解、分析的能力，利用数学工具求解科学研究中遇到的数学物理问题的能力，培养面向世界科学前沿和国家重要需求的具有国家情怀、科学精神、批判性思维、勇于创新的物理学拔尖人才.

目前数学物理方法课程在教育教学各个环节存在不少有待解决的问题，例如：如何革新教学理念来实现物理学专业的人才培养目标；如何合理有效地组织课堂教学来应对教学内容繁重而课时量逐年减少的现状[4]；如何重组创新教学内容，实现课堂教学内容与科技前沿紧密联系[5]；如何彻底打破“老师讲、学生听”填鸭式、被动式、沉默式的传统教学模式；如何改进教学手段，将抽象的理论和方法更加直观地表现出来；如何客观有效地进行教学评价；如何结合教学内容开展课程思政、立德树人.

2 改革创新的举措

2.1 革新教学理念

结合物理学专业培养创新型拔尖物理学人才的目标，秉承“格物致理、慎思笃行”的院训，课程教学团队确立了“以学生为中心，能力培养为目标，教学改革为手段，立德树人为宗旨”的教学理念.旨在通过本课程的学习加强学生的数学功底，提高物理素养，培养具有国家情怀、人文底蕴、科学精神、批判性思维[6]、勇于创新的物理学拔尖人才.

2.2 改革教学内容

为了展现数学物理方法课程“承上”的作用，体现其与高等数学的紧密联系，在复变函数部分教学过程中注重对比教学法.将复变函数的定义、极限、连续、导数、级数、积分等内容与高等数学中实函数的相应内容进行对比讲解，并通过实例使学生清楚它们之间的区别和联系.例如：在讲解复变函数极限、连续、复数列和复项级数收敛的充分必要条件时，强调这些充要条件的本质是建立在复变函数与高等数学之间的桥梁，通过充要条件把判断复变函数极限是否存在、函数是否连续、复数列和复项级数是否收敛的问题转化为判断实函数极限是否存在、是否连续、实数列和实项级数是否收敛的问题.又如：复变函数沿着有向曲线的积分可先等效为两个二元实函数的第二型曲线积分，然后通过选取曲线的参数方程最终将其化为定积分.再如：讲解留数定理时，通过实例使学生深刻认识到留数定理不仅能用来计算复变函数的围道积分，而且在实积分中有着广泛的应用，并且留数定理提供了一种区别于高等数学中利用牛顿-莱布尼茨公式求积分的方法——将求被积函数原函数的问题转为求复变函数在孤立奇点处留数的问题.为了提高上述对比教学法的教学效果，在相应章节授课前教师在线上班级群发布相应的复习和预习任务.

为了让数学物理方法课程更好地服务于后续“四大力学”等专业课程的学习，体现其“启下”的作用，在积分变换、数学物理方程部分教学过程中采用“知识点导向法”，即在讲授知识点的同时告知学生其可能应用于后续哪些课程的学习.例如，讲解分离变量法时，告知学生分离变量法可用于“量子力学”中定态薛定谔方程的求解，也可用于“电动力学”中导体尖劈附近的电场求解.基于“四大力学”等后续课程的需要及发展量子科技的需求，将教学内容延伸、重组、创新，增加了格林函数、勒让德级数、球谐函数等章节的教学投入，增加了非线性方程、小波分析等高阶内容.

2.3 创新教学方式

针对教学内容繁重而课时量逐年减少的现状，采用多媒体课件和板式教学相结合的教学方式，不仅展现了数学逻辑推导之美，又传递了更多物理知识.采用Maple或Mathematica等数学软件，简化了大量的数学推导过程，针对数学理论和求解方法过于抽象、不够直观、不容易理解的问题，采用基于Matlab和Origin等数学软件进行可视化[7]辅助教学.

2.4 教学模式创新

打破传统的填鸭式、被动式、沉默式的教学模式，以2017级为试点，开启6个课时的翻转课堂教学模式[8].教师根据教学内容，选择合适的章节，学生自讲自学，让学生成为课堂的主体，深度参与教学过程.同时，在超星泛雅平台建立了课程网站，并通过雨课堂、企业微信群等线上教学模式来补充和完善有限的线下课堂教学.线上辅助教学可以拓宽师生之间、学生之间的交流渠道，更重要的是线上辅助教学模式开放了学生的学习环境，增加了学生学习的自主权，使学生摆脱时间和地域的限制，自主地选择自己感兴趣的问题进行学习和交流，这样可以极大地培养学生的学习兴趣和创新能力[9].

2.5 完善教学评价方式

长期以来对教学效果的评价都局限于统计和分析学生的成绩分布以及学生评教结果.而上述单一片面的评教方式不能够真实反映出教师的教学水平和教学效果，因此如何客观有效地进行教改评价是一个非常重要的问题.本课程采用多元评价方式，通过以下几个方面对教学教改进行综合考核：①问卷调查，例如：学期末学生对课堂满意度的问卷调查、毕业生对四年所修课程的问卷调查等；②课程教学检查，例如：学校、学院教学指导委员会专家对课程的听课评价以及教师互评等；③教改成果评价，比如：教改论文、调研报告、教改项目、教学成果奖、一流课程申报等；④教师参加各类教学竞赛获奖情况，例如：全国高校青年教师教学竞赛、教育教学创新大赛等；⑤学生参与相关学术竞赛比例及获奖情况，例如：全国大学生数学竞赛、数学建模竞赛等.

2.6 课程思政、立德树人、教研融合

课前，根据教学内容，深度挖掘思政元素，编写思政案例；课堂中，充分发挥教学名师的人格魅力，展现渊博学识，准确自然地将思政元素融入，让学生在行为体验与情感体验中产生共鸣.与此同时，充分发挥教师的科研学术专长，寻找课堂教学内容与科学研究的交叉点、融合点，编写教研融合案例，指导本科生参与教师科研项目.

3 改革创新的成效

3.1 教学内容改革成效

学生反馈采用对比教学法使淡忘的高等数学知识被唤醒，数学基础得到了巩固和加强；根据学情增加常微分方程、傅里叶级数、完备正交函数集等内容的讲解为数学物理方法中新知识的引入和讲援做好了良好的铺垫，使得新知识的传授更加流畅，学生的学习效率、知识掌握程度明显提高；采用“知识点导向法”并适当增加格林函数、勒让德级数、球谐函数等章节的教学投入后，学生反馈学习量子力学、电动力学等后续专业课程的难度大大降低；增加非线性方程、小波分析等高阶内容对物理系专业学生将来研究生阶段的科学研究起到了知识辅助作用.

3.2 教学模式创新成效

以2017级为试点开启了4～6个课时的翻转课堂，打破了传统的“老师讲、学生听”、填鸭式、被动式、沉默式的教学模式，突出“以学生为中心”，真正地让学生成为课堂的主人，深度参与教学过程，提升课堂的活跃度，提高学生的学习兴趣.学生对课堂的满意度显著提高，2017和2019级学生评教分数创近几年新高(见图1).2020级物理学专业学生翻转课堂实施效果问卷调查显示：84.3%的同学认同课翻转课堂教学模式，92.1%的学生认为翻转课堂应控制在4～6课时，74.5%的学生认为翻转课堂有助于自主学习能力的培养和提高，66.7%的学生认为翻转课堂有助于分析问题和解决问题能力的提高，78.6%的学生认为翻转课堂更有助于交际能力的培养和提高，76.5%的学生认为翻转课堂有助于发现自身学习不足之处.

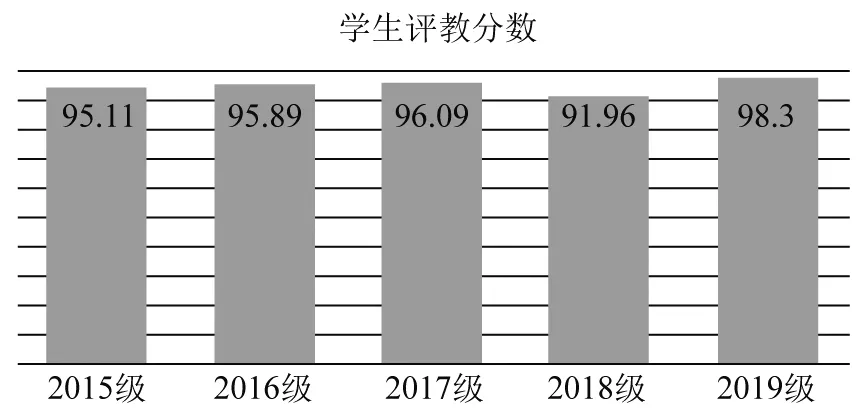
图1 2016-2019级物理学专业(国家基地)学生评教分数统计表

“翻转课堂”教学模式在一定程度上会压缩教师授课时间.从2020级开始该课程总课时从108压缩到80，翻转课堂的教学投入控制在4个课时.与此同时，授课教师可以在学生和教室空余(物理学专业拥有专有教室)的条件下，适当的延长相应的课时量.

3.3 教学方式创新成效

采用多媒体课件和板书相结合的教学方式来讲授这门课程，使教师能够在有限的课堂教学时间内既让学生享受到板书教学中精美的逻辑推导过程，又向学生传达了更多、更新的知识，体现了数学、物理两方面的有机结合和相互融合，强化了学科本身的优势.由于数学物理方法课程中有大量的数学推导，而这些推导过程往往是高等数学的重复，借助于Maple或Mathematica等数学软件不仅简化了这些数学推导，而且使学生掌握了更多、更新的技术手段，同时将学生的注意力转到对物理现象的理解和应用中去，大大提高了课堂的教学效率.采用基于MatLab和Origin等数学软件图像显示功能的可视化教学方式(见案例1和案例2)，能够将数学物理方法中各种抽象的概念和公式用图像表示出来，不仅能够使学生更加直观地理解具体的物理现象，同时也可以使学生掌握这些数学软件并将其应用到物理学各前沿领域的研究中.参加具体的科学研究，培养了学生的创新能力，为毕业设计打下了良好的基础.

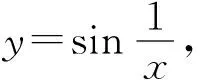
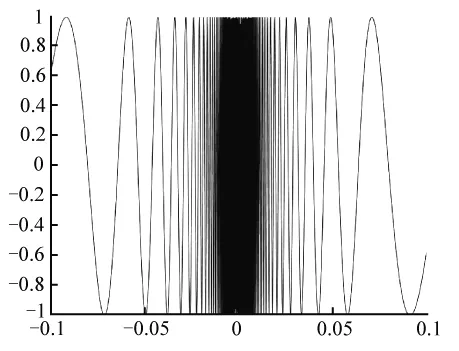
(a)x取值范围[-0.1, 0.1]

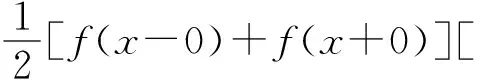
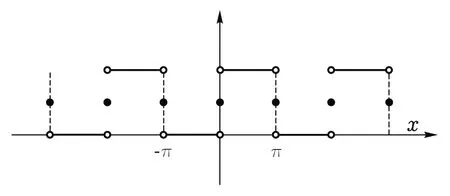
图3 周期函数的图像

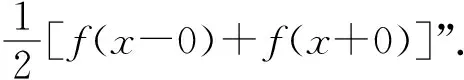
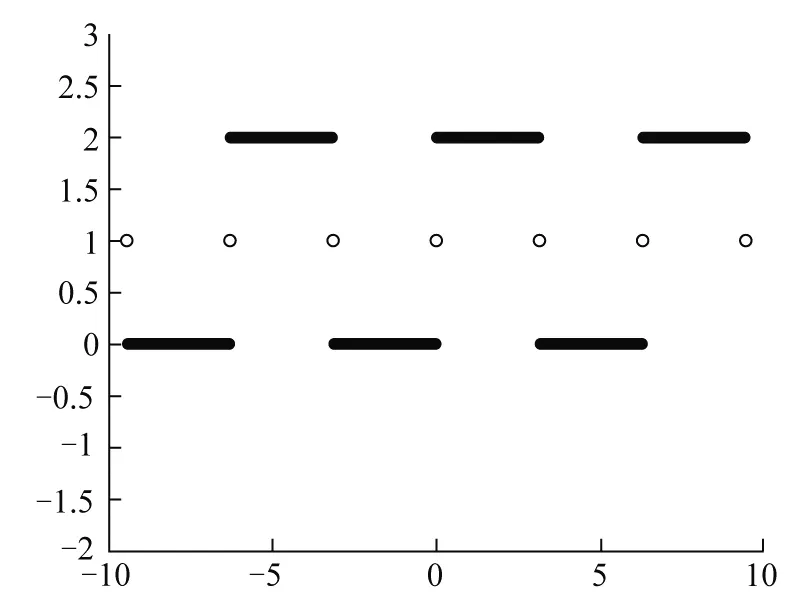
图4 函数傅里叶级数展开的图像

3.4 评教方式改革成效

面向全面综合的评教方式，课程组进行了一系列的教学改革与实践，取得了一定的成绩.2017级物理学本科毕业生问卷调查显示数学物理方法课程满意度排在所有专业课程中首位，2020—2021年度第2学期，学院教学指导委员会专家对课程听课评价为优秀.授课教师积极进行教学反思和总结，撰写教改论文，申报教改，申报国家级和省级“一流课程”，获批2021年度高等学校数学物理方法课程教学研究项目、2021年山西省高等学校教学改革创新项目.授课教师祝俊2021年参加山西大学物理电子工程学院青年教师教学基本功比赛并获得一等奖，2021年初参加山西大学第一届教育教学创新大赛.2019级物理学专业亢泽超同学获得中国大学生物理学术竞赛华北赛区三等奖.近两届(2018级和2019级)学生期末总评成绩的及格率、良好率和优秀率大幅度提高(见图5).

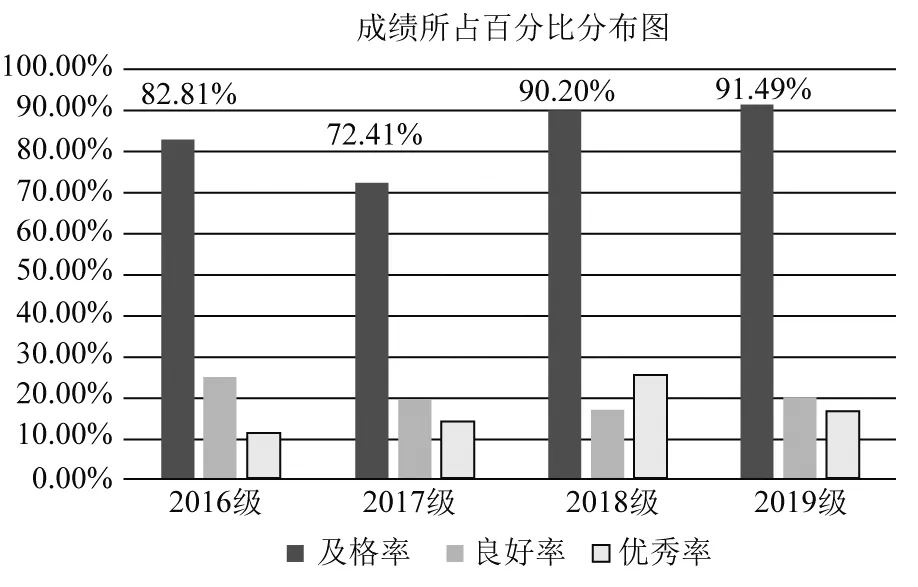
图5 2016-2019级学生期末总评成绩分析表

3.5 教研融合的成效

根据教学内容和教师的科研方向，找到课堂教学内容与科学研究的交叉点、融合点，围绕融合点进行内容展开，制作了教研融合案例集(见案例3、案例4)，实现了课堂教学服务科技前沿研究，科研成果反哺课堂教学的预期效果，体现了教研融合、教研相长.不仅如此，通过教研融合可以让本科生了解任课老师所从事的科学研究方向和内容，使本科生更早地进入科学研究，开展本科生科研训练.2018级两位同学(荚莉、霍龙龙)在授课教师的指导下围绕线性波在量子等离子体中的传播特性开展了相关的研究工作，并取得了一定的研究成果，相关研究成果“The propagation of linear waves in high-energy density magnetoplasmas by using a relativistic quantum magnetohydrodynamic model”已发表在J.Plasma Phys.杂志(SCI 3区)上.

案例3：讲授利用留数定理计算围道积分时，结合教师的科研方向，给学生介绍等离子体物理学中非常令人震惊的现象——朗道阻尼[7].朗道阻尼是一个未被预期的真实物理效应，是1946年朗道在对围道积分仔细分析过程中的纯数学发现，开始等离子体物理学家都不相信这个预言，直到1960年在实验室中得到了证实，等离子体物理学家才开始接受朗道阻尼，并从物理上去分析、解释这个效应.这是一个“先有数学结果，后有物理现象”的典型例子，体现了数学在物理学发展中的重要性.

案例4：结合教师的科研方向再给一个“先有物理含义，后有数学结果”的例子.大量文献资料表明：研究量子等离子体的真实物理环境是低温、高密度的致密天体等离子体，研究自旋量子等离子体则需要强磁场、低温物理环境.很自然会提出这样的问题“研究量子等离子体时，为什么需要低温、高密度和强磁场、低温物理环境，其中有什么物理原理？”追根溯源，我们得知：只有当电子热的德布罗意波长和等离子体系统中电子之间距离相当时量子效应才会显现.只有当电子自旋态的能量接近或者大于电子热能时才需要考虑自旋效应.通过电子热的德布罗意波长、等离子体系统中电子之间距离、自旋态的能量、热能的比较，计算发现在低温、高密度条件下，电子热的德布罗意波长会变得和电子之间距离相当；在强磁场、低温条件下，电子自旋态的能量才接近或大于电子热能.这是一个“先有物理原理分析，后有数学结果”的例子.

在教学过程中，利用案例3和4使学生深刻体会到数学和物理的融合，这恰恰正是数学物理方法课程的一大特点.

3.6 课程思政、立德树人

根据教学内容，深度挖掘思政元素，编写了思政案例初稿(见案例5、案例6)，主持物理电子工程学院课程思政建设项目一项[数学物理方法课程思政的切入与融合，山西大学物理电子工程学院课程思政建设项目(WDKCSZ202006)].

案例5：数学美学、文学、生态环境——太原“创城”、山西省经济转型.

中华诗词是传统文化的灿烂瑰宝.其经典篇章语精而意深，每吟之皆觉神情愉悦，欲醉其中.令人惊喜的是，数学含蓄、深奥的美无处不在，她的丽影也出现在古诗词里。北宋诗人邵雍的“一去二三里，烟村四五家，亭台六七座，八九十枝花”，这首诗《山村咏怀》通过列锦的表现手法把烟村、人家、亭台、鲜花等景象排列在一起，构成一幅田园风光图，并创造一种淡雅的意境，表达出诗人对大自然的喜爱与赞美之情.课堂教学中回顾数的发展，复习自然数时可以用邵雍这首诗引导学生认识到中国传统文化的博大精深，意识到保护生态环境的重要性.坚持人与自然和谐共生，树立和践行绿水青山就是金山银山的理念，坚持节约资源和保护环境的基本国策.

案例6：从“e”谈起，追根溯源、方得精髓——拥有自主知识产权

e是数学中一个重要的无理数，其近似值为2.71828……，但对于e的由来，学生们却知之甚少.在回顾数的发展，讲到无理数e时，引导学生做到追根溯源.e除了可以定义为数列极限外，还可以用级数来表示，在计算e的数值时，发现用级数形式要比极限形式更快得到其精确数值.教导学生们不仅要知其然，还要知其所以然，强调追根溯源，由此引申到“拥有自主知识产权”的问题上，通过华为起诉美国公司InterDigital的真实案例告诉学生必须走自主研发路线，用自己的品牌和技术核心，否则一切就会受制于人.

4 结语

综上所述，山西大学数学物理方法课程团队在教学理念、教学内容、教学模式、教学手段等方面尝试改革创新，取得了一定的成效.在此基础上笔者将继续优化课程设计，重整教学内容，改革教学模式，巩固教学团队，深化课程思政，努力把山西大学数学物理方法课程做得更好.