从时间演化角度讲解光电效应

何 峰

(上海交通大学 致远学院，物理与天文学院，上海 201800)

1900年左右，以维恩、勒纳德为代表的一批实验科学家获得了光和物质相互作用的丰富实验数据，但这些数据无法用基于麦克斯韦方程组的经典电动力学理论来解释.1905年，爱因斯坦发表了《关于光的产生和转化的一个试探性观点》的论文[1]，提出了光电子假说，完美解释了实验数据.这是近代物理发展中的一个光辉篇章.

现在我们对于光电效应的理解均参照爱因斯坦光电效应公式E=ћω0-W，其中E是光电子能量，ћ是约化普朗克常数，ω0是光子频率，W是逸出功.这个图像非常直观，这一解释方式也已经写进了教科书.一般高中和大学物理也是按照这个思路讲授光电效应[2,3].但是，当一束激光脉冲辐照原子时，原子并不预先知道光子的频率.在偶极近似下，激光场实际就是随时间演化的电场.对于原子而言，原子感受到随时间演化的振荡电场.那么，如何从时间演化的角度理解光电效应？

1 含时微扰论描述量子跃迁过程

爱因斯坦的光子理论可以用来判断能否发生光电效应并解释获得光电子能量的大小，但对于单个光子导致的光电离概率的大小无从给定.量子力学建立以后，根据含时微扰理论，可以计算发生光电离的概率.以一束激光和氢原子相互作用为例,相互作用之前，电子处于氢原子的基态|ψ0〉,吸收光子后电子跃迁至动量为p的末态|p〉(一般为平面波),初态和末态能量分别为E0和Ef=p2/2m，此处m是电子质量.在偶极近似下，含时微扰理论给出的跃迁振幅为[4]

(1)

其中F(t)是不依赖于空间的光电场，D是偶极矩，ω=(Ef-E0)/ћ，ti和tf是光电场开始和结束的时间.根据能量守恒，如果光子能量为ћω0，则末态的能量需要满足Ef=ћω0-E0.

从时间演化的角度来看，即使激光场已经演化了一半，原子仍然不能判断后面激光场的振荡行为.例如，图1中红色和黑色曲线是和原子相互作用的两种光电场.如图1所示，即使在t<0时刻两种光电场完全相同，但是在t=0时刻，原子仍然不知道t>0时刻这两种光场是否仍然相同.也就是说，在激光演化完成以前，原子无法精确判断光子的频率是多少，也不知道光子的能量.因此，我们会问，电子该吸收什么样的光子能量，跃迁至动量p为多大的末态？

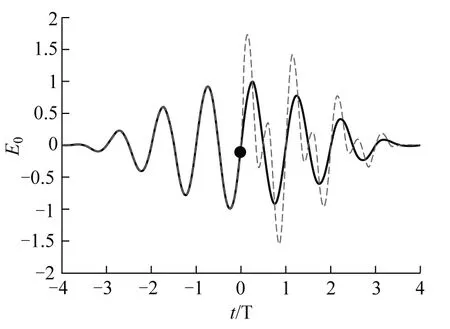
图1 激光脉冲和原子相互作用示意图(虚线和实线代表不同实验中可能使用的光场，圆点代表原子)

含时微扰论给出的跃迁振幅表达式实际上提供了从时间演化角度理解光电效应的基础.我们不妨根据图2分解表达式(1)给出的跃迁振幅.

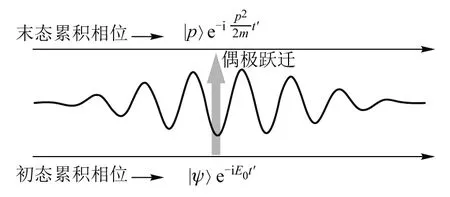
图2 量子跃迁的过程分解

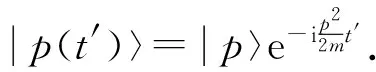
第2步：跃迁.在t′时刻，氢原子和光电场发生偶极相互作用.此刻，相互作用哈密顿量表述为F(t′)·D.在t′时刻的跃迁振幅为

〈p(t′)|F(t′)·D|ψ0(t′)〉=〈p|D|ψ0〉·F(t′)eiωt′

(2)

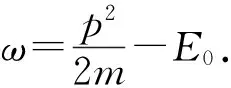
第3步：时间积分.在整个激光脉冲和原子相互作用的时间区间，在任意的t′时刻都有可能发生跃迁.既然不可能得知究竟在哪一时刻发生跃迁，那么根据量子力学的不确定性原理，需要把每个时刻的跃迁振幅相干叠加，即需要做时间积分.积分后的表达式即为方程(1).

2 不同时刻跃迁振幅的相干叠加

式(2)表明跃迁振幅携带了相位，且相位是t′的函数.因此，不同时刻的跃迁振幅的累加，必然存在干涉相长或者干涉相消的内涵.

设一束偏振方向沿着z轴的线偏振光电场可以描述为

(3)

其中F0是振幅，τ是脉冲的宽度.实际的光场是式(3)的实部，写成复数形式可便于计算.在下面的计算中，ω0=1 a.u.,T=2π/ω0，τ=10T,此处a.u.意为原子单位(atomic units).在偶极近似下，在时间区间[t1,t2]内的跃迁振幅可以用下式表述[5]：

(4)

对于较长脉冲，激光的包络[cos(πt/τ)]2可以近似看作常数.图3中的3条曲线分别对应积分区间[t1,t2]=[0,0.1T],[0,T]和[0,10T]3种情况的跃迁概率|Mp(t1,t2)|2.可以看出，当积分区间非常小时，原子尚未感受到光电场的振荡，甚至不清楚这是直流场还是交变场，因此无法知道光子的频率信息.这导致末态动量的分布非常宽.而当积分区间为一整个周期时，原子基本获悉在这段时间内光场的振荡频率，基本有了光子能量的概念，这个时候末态动量的分布呈现两个明显的峰，这两个峰对应的光电子能量为0.5 a.u..当积分区间为10T时，在这段相对较长的时间内，原子非常好地感受到了周期性的振荡，非常明确地知道了光场的振荡频率，精确获悉光子的能量.原子吸收光子后，根据能量守恒，光电子的能量必须为0.5 a.u.，也即在动量分布上精确对应p=±1 a.u.，如图3短线所示.可以想象，如果积分区间无穷小，光电子的动量分布可以无穷宽；如果积分区间无穷大，光电子的动量分布由出现在±1 a.u.的两个δ函数支配.

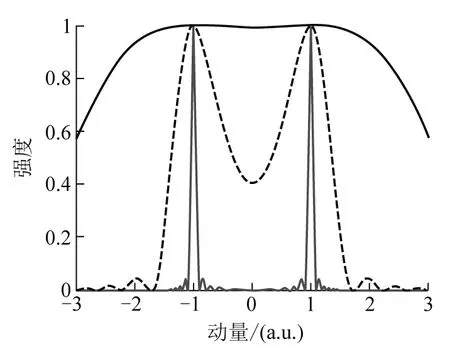
图3 光电子动量分布(点划线、实线、短线分别对应积分区间是[t1,t2]=[0,0.1T],[0,T]和[0,10T].)

基于以上分析，我们可以知道，在每个瞬时，电子可以吸收任意的光子能量.在不同时刻发生的跃迁振幅相干叠加，干涉相消和干涉相长使得最后只有满足能量守恒关系的跃迁振幅被保留下来.

3 含时微扰理论和费曼路径积分

根据费曼路径积分理论，从A传播到B的概率幅可以描述为[6]

(5)

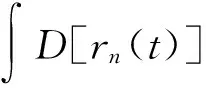
含时微扰理论和费曼路径积分的表达式在数学形式上有很多相似性.式(1)中，对最终跃迁振幅有较大贡献的积分元，其相位对时间取极值，即

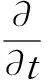
(6)

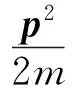
4 杨氏双缝干涉

有了在时间维度对光电效应的深刻理解后，我们可以引导学生设计时域的杨氏双缝干涉.例如，利用两束超短激光脉冲和原子相互作用，如图4(a)所示.原子有可能被第一束激光电离，也有可能被第二束激光电离.在这个实验中，两束光脉冲就相当于传统杨氏双缝干涉实验中的双缝，脉冲的宽度相当于狭缝的宽度，两束光脉冲的时间延迟相当于双缝之间的间隔.这是用电子的德布罗意波演示双缝干涉的方法.通过控制两束光脉冲的相关参数，可以控制双缝干涉的结果.图4(b)中黑色实线给出了在图4(a)中的激光场作用下，光电子的动量分布.图4(b)中点划线对应于只使用图4(a)中一束光脉冲作用得到的光电子动量分布.在两束光的作用下，在p=±1 a.u.处，原来单一的峰劈裂了，呈现了典型的杨氏双缝干涉的结果.在这个实验中，原子并不预先知道有两束光脉冲要和原子相互作用；原子只和第一束光作用后，不可能呈现杨氏双缝干涉的结构；只有当两束光都作用完了，杨氏双缝干涉才真正完成.因此光电子动量分布也是不同时刻光电离事件的相干叠加.

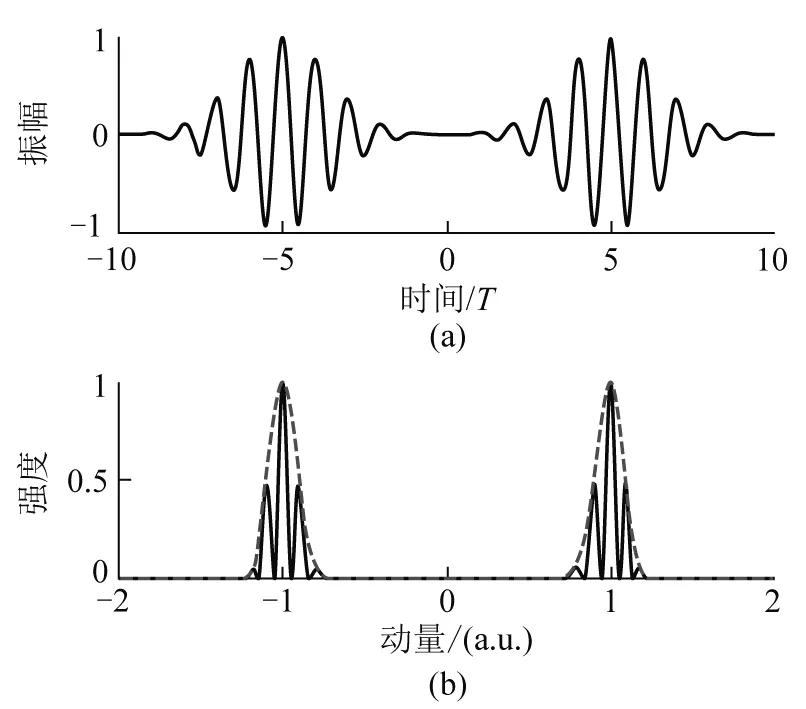
图4 (a)两束光脉冲示意图[只取式(3)实部]；(b)在激光偏振方向的光电子动量分布(纵轴都已经归一化)

5 总结

基于含时微扰的量子跃迁表达式，本文提出了从时间演化角度理解光电效应的思路.时域和频域两个维度对光电效应的解释互相补充，而且存在着内在关联.式(3)实际就是激光场的傅里叶变换.式(3)中积分区间不同，则计算结果也不同.根据不确定性原理ΔtΔE≥ћ/2，积分区间越短即Δt越小，那么光子能量的不确定度ΔE就越大.在某个非常短的时间区间内发生的光电效应实际上仍然可以用爱因斯坦光电效应公式来描述，只不过这段时间内光子的频率本来就是不确定的.不同时刻的跃迁事件相互干涉，导致时间演化结束后的光电子动量分布符合爱因斯坦光电效应公式描述的期望值.从时间演化的角度理解光电效应有助于学生从因果律上加深对基本物理过程的认识，可以启发学生融会贯通不同知识点，拓宽对杨氏双缝干涉的理解[6].