基于微分平滑理论的MMC 电容电压波动无源一致性控制方法

薛 花，扈曾辉，陈 程，王育飞，杨兴武

（上海电力大学电气工程学院,上海市 200090）

0 引言

近年来,模块化多电平换流器（modular multilevel converter,MMC）在大规模可再生能源并网方面体现出广阔应用前景,而高效的电容电压波动抑制对于确保MMC 的经济可靠运行具有重要工程意义［1-3］。实际工程中,常采用环流注入法抑制MMC 电容电压波动,通过准确快速求取注入环流的幅值和相角,设计闭环控制律,实现子模块电容电压均衡。但可再生能源发电的波动性与随机性导致MMC 运行工况多变,合适的环流注入需实现期望轨迹准确在线求取与快速稳定跟踪,因此考虑存在不确定性扰动情形下注入环流期望轨迹生成与闭环控制律设计成为拓展MMC 工程应用的关键所在。

在注入环流期望轨迹生成方面,通常采用查表法,但查表法无法根据MMC 运行工况的变化而准确给出最优注入环流期望轨迹,影响电容电压波动抑制效果［4］。为了弥补查表法的不足,文献［5-6］提出通过MMC 输出电流和调制信号瞬时值求取注入环流参考值,提升了准确性,但桥臂电流均方根显著增加,使器件功率损耗增大。文献［7］通过精确解析MMC 系统损耗与注入环流间的非线性关系,可根据MMC 运行工况求取最佳注入环流值,但数值解析法计算复杂、在线运算量大、工程应用较困难。文献［8］采用重复控制器生成二倍频环流参考值,计算简单,效果较优,但对相位精确采样要求较高,且未能解决系统参数摄动对重复控制器性能的影响。因而,考虑外部不确定性干扰和未建模误差,如何兼顾方法的简洁性、鲁棒性以及波动电容电压与注入环流间非线性关系解析的准确性,是注入环流期望轨迹设计面临的难点问题。

在闭环控制律设计方面,目前主要采用传统矢量控制方法,设计比例-积分（PI）控制器,通过dq解耦方式,实现系统在期望工作点稳定运行［9-10］。文献［5］提出并联多个比例-谐振（PR）控制器,实现更优的注入环流偶次谐波期望轨迹跟踪性能。但PI、PR 控制器参数基于MMC 小信号模型设计,由于MMC 本身具有强非线性特征,局部线性化的小信号模型仅能保证闭环控制系统具有较窄的稳定域,当存在不确定性干扰时系统运行稳定性受到挑战［11］。无源性控制（passivity-based control,PBC）方法将非线性系统视为能量转换器,通过全局能量函数整形,实现系统能量在期望工作点渐近趋于稳定［12］。文献［13-14］提出基于欧拉-拉格朗日（Euler-Lagrange,EL）模型的MMC 并网电流PBC 方法,验证了PBC 方法响应快速、稳定域宽的特点。但基于EL 模型的无源性控制律设计需沿Lagrangian 期望轨迹对系统能量函数进行求逆计算,限制了PBC 方法的工程应用。因而,突破能量函数求逆约束,提出形式简单、稳定性好、多目标集成的PBC 方法是实现闭环控制律性能提升需解决的关键问题。

为实现MMC 电容电压波动快速在线抑制,本文从系统非线性本质出发,应用微分平滑理论生成注入环流期望轨迹,避免非线性关系的近似化处理,确保MMC 运行工况变化情形下注入环流期望轨迹求取精度；设计MMC 子模块电容电压系统端口受控耗散哈密顿（port-controlled Hamiltonian with dissipation,PCHD）模型,提出结构简单的无源一致性控制方法,实现注入环流期望轨迹跟踪与三相电容电压均衡控制双目标同步达成,且系统具有全局渐近稳定性。在MATLAB/Simulink 环境下搭建七电平MMC 仿真模型,验证所提基于微分平滑理论的无源一致性控制方法的可行性与有效性。此外,借助dSPACE 平台建立MMC 实验系统,验证所提基于微分平滑理论的无源一致性控制方法抑制MMC 电容电压波动的有效性与可行性。

1 注入环流期望轨迹准确求取

三相MMC 桥式电路结构如图1 所示。MMC每相有上、下2 个桥臂,每个桥臂由N个相同的子模块（SM）级联组成,Lm、Rm分别为桥臂电感、桥臂电阻,Udc、idc分别为直流侧电压、电流,ipj、inj分别为流过j（j=a,b,c）相上、下桥臂的电流,upj、unj分别为j相 上、下 桥 臂 电 压,icirj为 相 间 环 流,ej、ij分 别 为MMC 的j相输出电压、电流,L、R分别为交流侧电感、电阻,uj为交流侧j相电压,usm为子模块输出电压,ucpa、ucna分别为上、下桥臂子模块电容电压。由于可再生能源发电具有随机性与波动性,导致MMC 运行工况多变,注入环流期望轨迹实时变化,因此快速准确的注入环流期望轨迹在线生成是实现子模块电容电压波动抑制的前提条件。

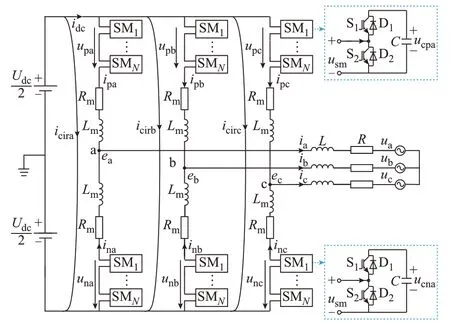
图1 三相MMC 电路结构及子模块拓扑Fig.1 Circuit structure of three-phase MMC and submodule topology

由图1 分析可知,MMC 电容电压波动Δucpa/cna与注入环流的关系如式（1）所示［4］。

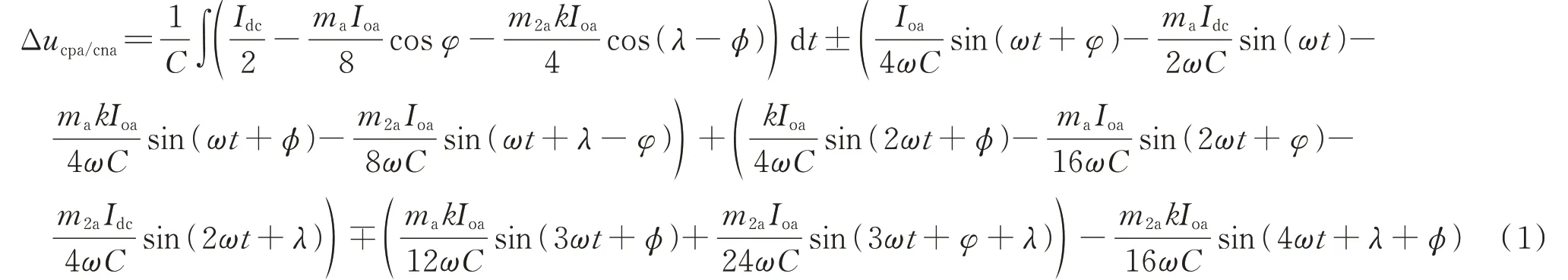
式中：C为子模块电容值；Idc为直流电流分量幅值；Ioa为交流侧输出电流幅值；ma、m2a分别为直流分量、二倍频分量调制比；ω为输出电压角频率；φ为输出电流基频分量相位；φ为输出电流二倍频分量相位；k为注入比；λ为初始相角。

由式（1）分析可知,MMC 波动电容电压与注入环流间存在强非线性映射关系,采用数值解析法,可由输出电流和调制比求取注入环流最优幅值与相角,但计算量复杂,不利于工程应用。针对这一问题,应用微分平滑理论,通过构建平滑输入变量、状态变量与平滑输出变量及其有限阶时间导数间的微分关系,实现MMC 波动电容电压与注入环流间非线性映射超平面的线性化转化,仅需设计简单的线性化状态反馈控制律,即可实现注入环流期望轨迹的快速准确求取,能够随MMC 运行工况变化自主调整期望轨迹生成。

以MMC 的a 相为例,选取上、下桥臂子模块电容电压γ=[γ1,γ2]T=[upa,una]T为平滑输入变量,上、下 桥 臂 电 流ξ=[ξ1,ξ2]T=[ipa,ina]T为 状 态 变量,上、下 桥 臂 子 模 块 电 容 电 压μ=[μ1,μ2]T=[upa,una]T为平滑输出变量。由图1 分析可知,根据基尔霍夫电压定律（KVL）,所设状态变量满足式（2）［15］：

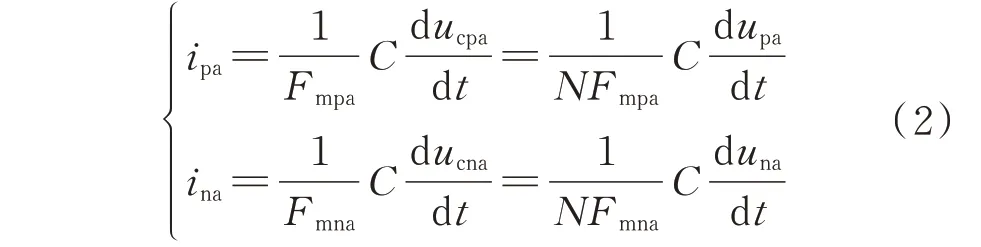
式中：Fmpa、Fmna分别为上、下桥臂开关函数；ucpa、ucna满足upa=Nucpa,una=Nucna。

根据式（2）可得,平滑输入变量、状态变量可由平滑输出变量表示为：

由式（3）可知,状态变量和平滑输入变量可由平滑输出变量及其有限阶的时间导数表示。根据微分平滑理论［16］,由平滑输入变量γ、状态变量ξ、平滑输出变量μ所描述的波动电容电压与注入环流间非线性映射满足平滑特性,所述非线性系统为平滑系统。

若定义上、下桥臂子模块电容电压参考值为μ*=[μ,μ]T,则可设计线性化状态反馈控制律,即微分平滑控制律为：

式中：K1和K2为微分平滑控制器参数。

式（4）可写为：

将式（5）代入式（3）,可得状态变量表达式,即上、下桥臂电流方程为：

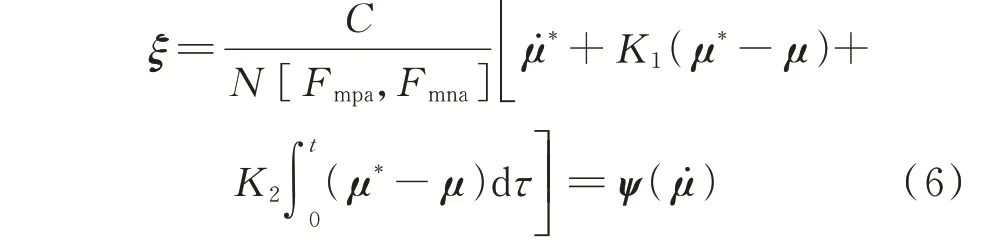
由式（3）和式（6）可知,平滑输出变量μ与状态变量ξ、平滑输入变量γ能够各自张成超平面,超平面是线性的,具有动态可逆特性［17］。因此,求解逆系统实现状态反馈控制时无须求解微分方程,设计简单的线性化状态反馈控制律,即可求取状态变量期望轨迹,避免了非线性关系的近似化处理,确保了注入环流期望轨迹的求取精度,同时所提微分平滑控制律简单、计算量小,克服了数值解析法［7］运算复杂、难以工程应用的不足。

由上、下桥臂电流与环流的关系,结合式（6）,可得MMC 各相注入环流期望轨迹i为：

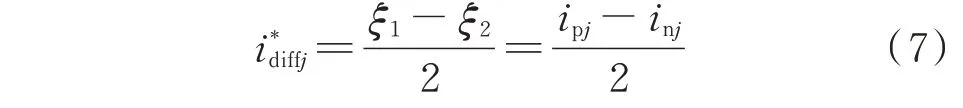
考虑可再生能源发电波动性引起的输入扰动、未建模误差以及不确定性干扰的存在,将系统平滑输出误差εi（i=1,2,3,4）定义为：

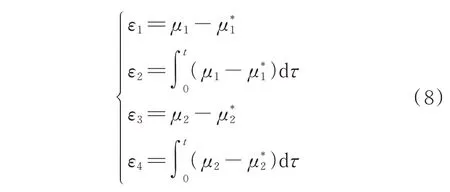
为量化分析平滑输出误差对状态变量的影响,设置半正定能量函数V为：

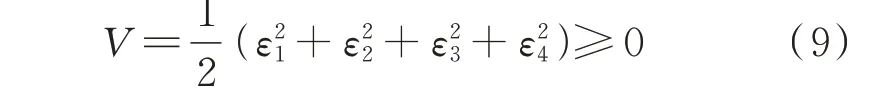
对式（9）进行求导可得：

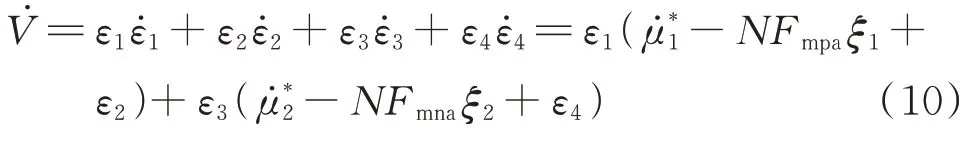
将式（6）代入式（10）可得：

当K1,K2＞0 时,由式（9）和式（11）可知,采用微分平滑控制律式（5）,可实现MMC 波动电容电压与注入环流构成的平滑系统渐近收敛至期望工作点,当输出变量稳定时平滑系统可保持稳定［18-19］。因而,所提微分平滑控制方法具有较宽稳定域和较强鲁棒性,克服了重复控制方法［8］对不确定性干扰和未建模误差较敏感的不足。

2 无源一致性闭环控制方法设计

2.1 MMC 电容电压波动系统PCHD 模型

为了避免EL 模型需沿Lagrangian 期望轨迹进行求逆计算的约束,建立MMC 电容电压波动系统PCHD 模型,求解能量函数偏微分方程,即可实现在期望平衡点的全局渐近稳定,为形式简单的无源性控制律设计准备条件。

dq轴坐标系下,MMC 波动电容电压与环流之间满足：

式中：ucird、ucirq分别为子模块波动电容电压d轴、q轴分量；icird、icirq分别为环流d轴、q轴分量；ω0为基波角频率。

以MMC 电容电压波动抑制为目标,选取PCHD 模型状态变量、输入变量和输出变量分别为：

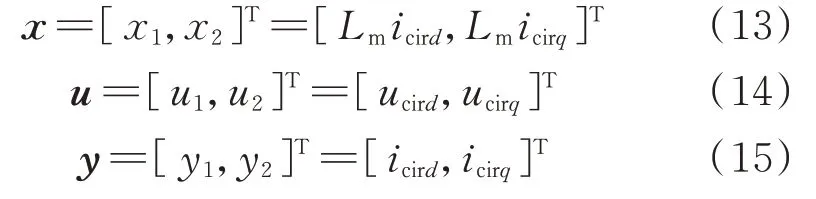
设计正定二次型全局能量函数为：

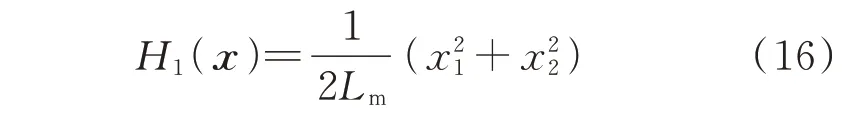
由式（12）和式（16）可得,MMC 电容电压波动系统PCHD 模型方程式可写为：

将式（16）代入式（17）,可得MMC 全局能量函数的导数为：

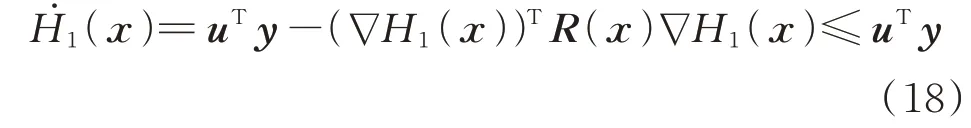
由耗散不等式（18）分析可知：非线性映射u→x满足输出严格无源定义,因此MMC 电容电压波动系统具有无源特性［20］。根据无源性控制理论［21］,由MMC 全局能量函数式（16）和电容电压波动系统PCHD 模型方程式（17）,设计无源性控制器,无论系统初始状态如何,都可确保闭环控制系统渐近收敛于期望工作点。

2.2 实现双目标的无源一致性控制器设计

由式（7）求取MMC 三相注入环流期望轨迹i,经dq坐标变换,可得dq两相注入环流期望轨迹i、i。结合式（15）,设计形式简单、稳定域宽的无源一致性控制律,避免矢量控制方法依赖于MMC模型参数、稳定域窄的不足,实现注入环流期望轨迹快速跟踪,且同时达成电容电压波动抑制与三相电容电压均衡控制双目标。

设置dq坐标系下MMC 电容电压波动系统的期望平衡点为：

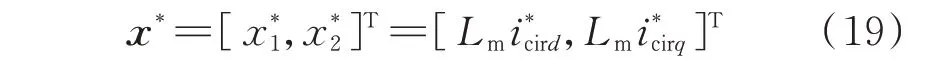
为使闭环控制系统在期望平衡点x*处能量达到最小值,即闭环控制系统能够收敛至期望平衡点,构造MMC 电容电压波动系统期望的全局能量函数为：

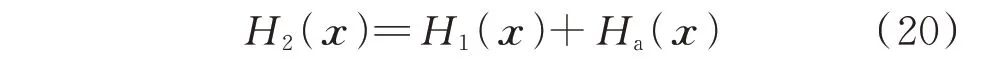
式中：Ha(x)为通过无源性控制律注入系统的能量,

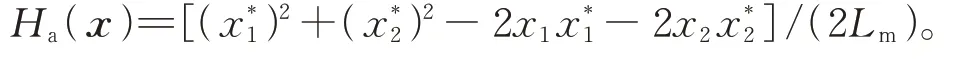
由式（19）,定义注入环流期望轨迹跟踪误差为：

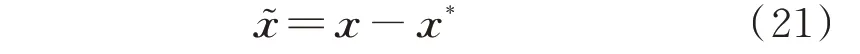
式中：x͂=[x͂1,x͂2]T。

为了实现注入环流期望轨迹的渐近跟踪,即

将式（20）代入PCHD 模型方程式（17）,可得：

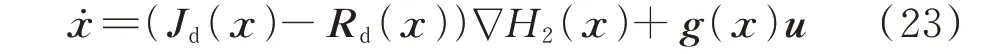
式中：∇H2(x)=∂H2(x)/∂x；Jd(x)为系统期望的互联矩阵,满足Jd(x)=J(x)+Ja(x)=−J(x),其中Ja(x)为注入的耗散矩阵；Rd(x)为系统期望的阻尼矩阵,满足Rd(x)=R(x)+Ra(x)=R(x)＞0,其中Ra(x)为注入的阻尼矩阵。

将式（20）代入式（23）,可得PBC 控制律为：

对于式（24）,在确保全局能量函数快速收敛至期望平衡点的前提下,合理选取Ja(x)=0,仅需注入较小的阻尼矩阵Ra(x),即可实现MMC 注入环流快速跟踪期望轨迹。而较小的阻尼矩阵Ra(x)表明：PBC 方法可有效控制系统内部耗散能量,仅需较小注入环流,以最小系统能耗实现子模块电容电压波动抑制,优化系统能量分配,提升MMC输出效率。

为了实现MMC 相间电容电压均值一致性,在满足电容电压波动抑制的同时,增加注入环流期望轨迹同步跟踪目标,即

根据式（25）,设计一致性控制律为：

其中,因MMC 三相电容电压期望轨迹一致,取一致性控制增益α=1。

将一致性控制律式（26）作为状态误差,引入无源性控制律中期望的全局能量函数,则每一相注入环流期望轨迹跟踪控制律都包含了相邻相的跟踪误差,有益于提升注入环流期望轨迹跟踪同步性,实现MMC 三相电容电压均值零偏差。

将式（26）代入式（20）,则期望的全局能量函数可改写为：

对式（27）求导可得：

式中：∇H3(x)=∂H3(x)/∂x。

将式（28）代入式（24）,可得无源一致性控制律：

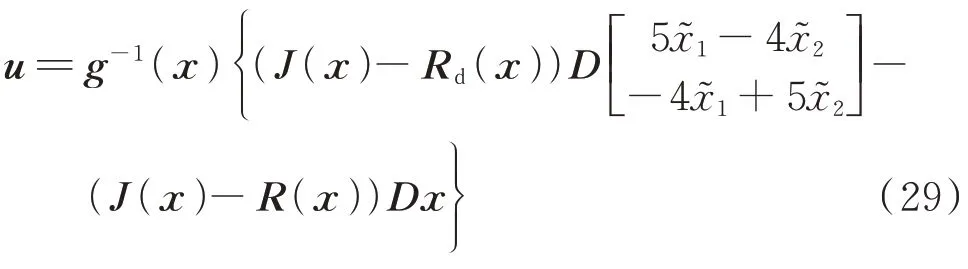
即

式 中：A1=8ω0Lm−5(Rm+ra1),A2=10ω0Lm+4(Rm+ra2),其 中ra1、ra2为 正 阻 尼 注 入 系 数；B1=−10ω0Lm+4(Rm+ra1),B2=−8ω0Lm−5(Rm+ra2)；C1=2ω0Lm,C2=−2ω0Lm；D1=D2=Rm。

由式（30）可知,选择适当的ra1和ra2可提升注入环流期望轨迹跟踪的快速性；相邻相状态变量跟踪误差的引入,可保证环流期望轨迹跟踪的同步性,实现MMC 电容电压均值无偏差,同时达成注入环流期望轨迹跟踪与三相电容电压均衡控制双目标。

基于微分平滑理论的MMC 电容电压波动无源一致性控制方法设计整体控制框图如图2 所示,注入环流期望轨迹求取方法兼顾算法的简洁性和准确性,实现MMC 运行工况变化情形下注入环流期望轨迹的自动寻优；闭环控制方法的设计兼顾稳定性需求与跟踪快速性,实现电容电压波动抑制和三相电容电压同步跟踪双目标的同时达成,提升闭环控制方法的性能。图2 中：G1,G2,…,G2N为各子模块开关信号；np,abc、nn,abc分别为三相上、下桥臂子模块导通个数；upj,diff、unj,diff分别为上、下桥臂电压调制信号。

图2 基于微分平滑理论的MMC 电容电压波动无源一致性控制框图Fig.2 Block diagram of passivity-consensus based control for capacitor voltage fluctuation suppression of MMC based on differential flatness theory

3 稳定性分析

利用La Salle 不变集定理,证明无源一致性闭环控制系统的全局渐近稳定性［22］。

将期望的全局能量函数H3(x)选为Lyapunov函数,则无源一致性闭环控制系统总能量函数H3(x)的导数可表示为：

由 式（34）可 知,当Ḣ3(x)=0 时,有x1=x,x2=x,则系统在{x∈Rn|Ḣ3(x)=0}内的解仅有{x∈Rn|x=x*},即系统的最大不变集为x=x*。

由La Salle 不变集定理可得,无源一致性闭环控制系统收敛于最大不变集,即在平衡点处渐近稳定。

又由式（31）可知,H3是径向无界的,即当‖x‖→∞时,H3(x)→∞,则无源一致性闭环控制系统在平衡点x*处是全局渐近稳定的。

4 基于MATLAB 的仿真结果分析

为验证所提基于微分平滑理论的无源一致性控制方法的可行性与有效性,在MATLAB/Simulink环境下搭建七电平MMC 仿真模型［23］。将本文方法与基于查表法的矢量控制方法［4］、基于数值解析法的矢量控制方法［6］进行电容电压波动抑制性能对比分析,MMC 系统仿真参数如附录A 表A1 所示,各方法控制参数如附录A 表A2 所示。在MMC 系统稳态运行情形下,采用本文方法进行MMC 电容电压波动抑制性能仿真测试。在t=0.3 s 时启动子模块电容电压波动抑制控制方法,仿真波形如图3 所示。

图3 稳态运行条件下采用无源一致性控制方法的MMC 电容电压波动抑制仿真波形Fig.3 Simulation waveforms of capacitor voltage fluctuation suppression of MMC with passivity-consensus based control method under steady operation condition

三相上桥臂子模块电容电压波形如图3（a）所示。由图3（a）分析可知,在未采用子模块电容电压波动抑制方法前,三相上桥臂子模块电容电压波动幅度较大,在t=0.3 s 时,应用所提控制方法,MMC电容电压波动快速减小,与理论分析结果一致,效果明显。所提基于微分平滑理论的无源一致性控制方法实现了注入环流期望轨迹的快速跟踪,暂态过渡时间短、无超调,三相电容电压均值一致性好、偏差较小。

注入环流d轴、q轴分量期望轨迹与跟踪波形分别如图3（b）和（c）所示。由图3（b）和（c）分析可知,采用微分平滑控制方法能够准确生成注入环流期望轨迹,采用无源一致性控制方法实现了d轴、q轴分量期望轨迹的快速准确跟踪,稳态误差小。

网侧三相电压、三相电流波形分别如图3（d）和（e）所示。由图3（d）和（e）分析可知,采用注入环流方法实现了子模块电容电压波动抑制,且不影响MMC 交流侧输出外特性,网侧系统保持平稳运行。

1）情形1：有功功率参考值为46 MW,无功功率参考值为零

在情形1 下,分别采用基于查表法的矢量控制、基于数值解析法的矢量控制和本文所提基于微分平滑理论的无源一致性控制方法对MMC 电容电压波动抑制性能进行仿真测试。在t=0.3 s 时,启动子模块电容电压波动抑制策略,仿真波形如图4 所示。

a 相上桥臂子模块电容电压波形如图4（a）所示。由图4（a）分析可知,MMC 稳态运行情形1 下,在t=0.3 s 时启动子模块电容电压波动抑制方法,3 种方法均能起到较好的抑制效果,电压波动明显减小。采用矢量控制方法,子模块电容电压波形畸变较明显,所含谐波较多；采用本文所提基于微分平滑理论的无源一致性控制方法,a 相上桥臂子模块电容电压幅值略大于矢量控制方法输出结果,但能够较好维持子模块电容电压波形的对称性,畸变率小,谐波少。

注入环流d轴、q轴分量期望轨迹与跟踪波形分别如图4（b）和（c）所示。由图4（b）和（c）分析可知,查表法、数值解析法与本文所提微分平滑控制方法都能根据当前子模块电容电压求取注入环流期望轨迹,在t=0.3 s 时电容电压波动抑制方法启动,查表法动态响应较数值解析法和本文方法更为快速,但查表法环流期望轨迹的准确生成与幅值、相角的准确检测密切相关；数值解析法与本文方法较查表法暂态过程更短,稳态误差更小。

a 相环流波形如图4（d）所示。由图4（d）分析可知,采用环流注入方式可实现子模块电容电压波动抑制,却会使得MMC 相间环流增大。较传统矢量控制方法,本文方法注入环流幅值最小,由于无源性控制方法充分利用电容电压波动系统内含能量,通过全局能量函数整形,实现系统能量最优调度,仅需较小环流注入,即可实现与矢量控制方法相同的电容电压波动抑制效果。

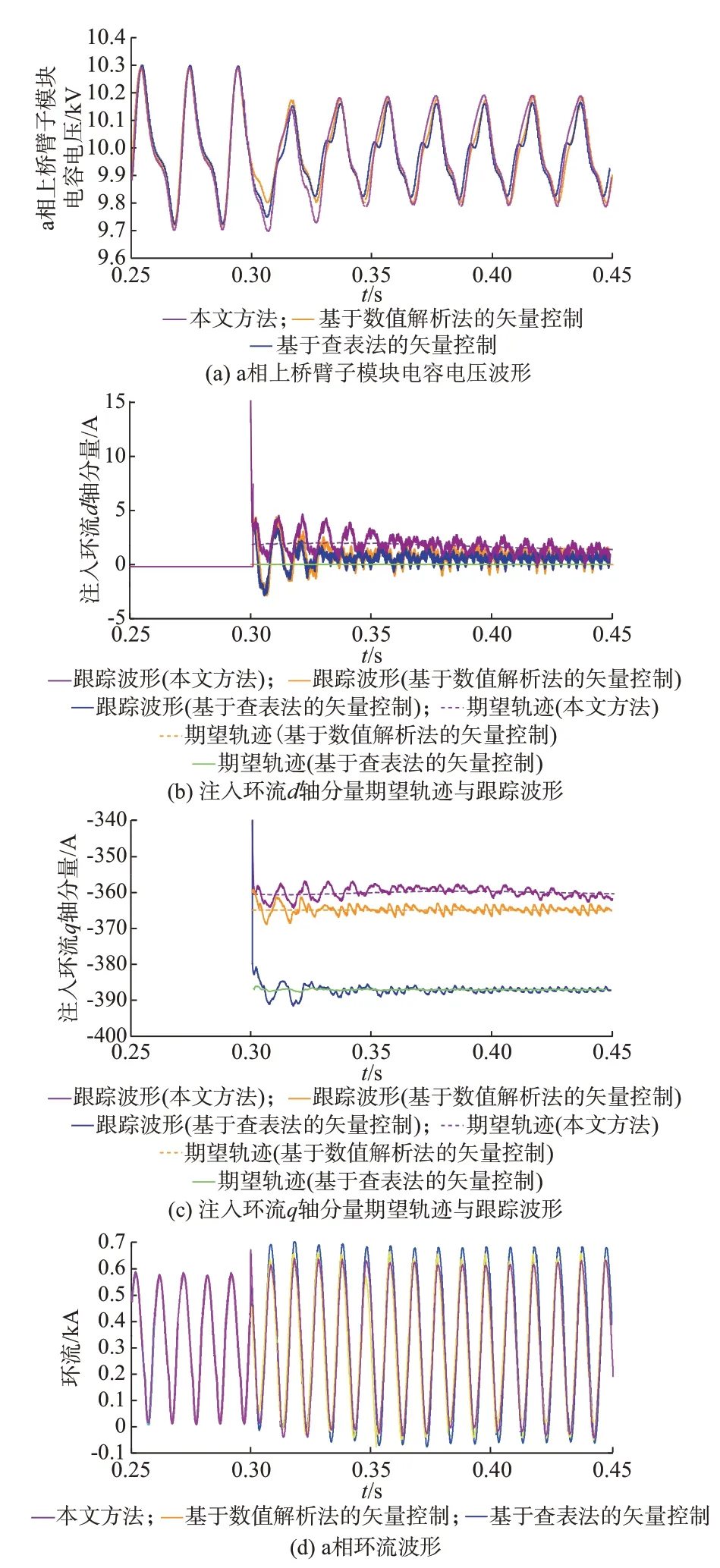
图4 情形1 下3 种方法的a 相电容电压与环流仿真波形Fig.4 Simulation waveforms of capacitor voltage and circulating current of phase a with three methods in scenario 1

为量化比较3 种方法抑制MMC 电容电压波动的性能,进一步对a 相子模块电容电压和环流进行5 个周期快速傅里叶变换（FFT）分析,如图5 所示。分析结果分别如表1 和表2 所示。

图5 MMC 子模块电容电压与环流FFT 分析Fig.5 FFT analysis of submodule capacitor voltage of MMC and circulating current

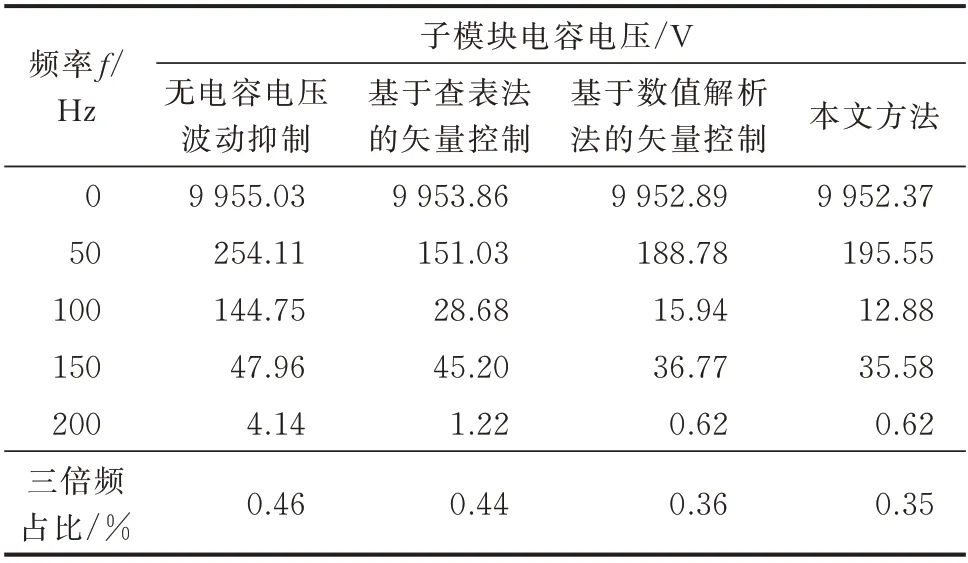
表1 3 种方法的子模块电容电压谐波分析Table 1 Harmonic analysis of submodule capacitor voltage with three methods

由图5 和表1、表2 分析可知：3 种方法均能抑制子模块电容电压波动,应用本文所提基于微分平滑理论的无源一致性控制方法,能够实现各频率谐波含量最少、子模块电容电压三倍频占比最小,因而MMC 电容电压波形对称性好、畸变率小、环流二倍频占比最小、MMC 环流增幅最小,实现了MMC 电容电压波动抑制与环流控制综合性能的最佳平衡。

表2 3 种方法的环流谐波分析Table 2 Harmonic analysis of circulating current with three methods

2）情形2：有功功率参考值为零,无功功率参考值为46 Mvar

在情形2 下,分别采用基于查表法的矢量控制、基于数值解析法的矢量控制和本文所提基于微分平滑理论的无源一致性控制方法对MMC 电容电压波动抑制性能进行仿真测试。在t=0.3 s 时,启动子模块电容电压波动抑制策略,仿真波形如图6 所示。

a 相上桥臂子模块电容电压波形如图6（a）所示。对比图4（a）和图6（a）可知,在视在功率保持不变的情况下,MMC 稳态运行情形2 下子模块电容电压波动幅度增大,不对称性和波形畸变较稳态情形1 更为显著。采用基于查表法的矢量控制方法,子模块电容电压波形畸变最为明显；采用基于数值解析法的矢量控制方法波形畸变较小,但电容电压波动幅度大于本文方法；本文方法响应快速,调节时间短,电容电压波动幅度小,依然保持了较优的控制性能,验证了本文方法能够在MMC 宽运行范围内实现期望的电容电压波动抑制性能。

注入环流d轴、q轴分量期望轨迹和跟踪波形分别如图6（b）和（c）所示。对比图4（b）和图6（b）、图4（c）和图6（c）可知,零功率因数运行条件下,注入环流d轴分量跟踪性能与理想功率因数运行条件下相似,但注入环流q轴分量幅值显著减小,查表法的注入环流q轴分量期望轨迹出现明显波动,数值解析法与本文方法能够保持注入环流期望轨迹平稳,比查表法更适应MMC 宽运行范围。基于查表法的矢量控制方法注入环流d、q轴分量轨迹跟踪虽幅值最小,但波动幅度明显,是导致a 相环流畸变的主要原因；基于数值解析法的矢量控制方法和本文方法注入环流期望轨迹跟踪快速、稳态误差小,且本文方法注入环流幅值小于基于数值解析法的矢量控制方法,表明本文方法兼顾了确保电容电压波动抑制效果与较小注入环流代价间的平衡。

图6 情形2 下3 种方法的a 相电容电压与环流仿真波形Fig.6 Simulation waveforms of capacitor voltage and circulating current of phase a with three methods in scenario 2

a 相环流波形如图6（d）所示。比较图4（d）和图6（d）可知,在MMC 稳态运行情形2 下,环流直流分量为零,电容电压波动抑制方法启动后,环流幅值减小。基于查表法的矢量控制方法环流畸变明显,控制性能不及稳态运行情形1；基于数值解析法的矢量控制方法和本文方法环流稍有畸变,但依然保持了较好的动静态响应性能,本文方法环流幅值更小,控制性能较优。

对3 种抑制方法下MMC 电容电压平衡度进行测试,在情形1 下t=0.6～0.8 s 期间,3 种方法MMC三相子模块电容电压波形如图7 所示。由图7 分析可知,采用矢量控制方法的MMC三相子模块电容电压波形畸变较明显,各相子模块电容电压均值偏差较大；采用本文方法,将相邻相注入环流期望轨迹跟踪误差作为状态误差引入无源性控制律,实现了三相子模块电容电压均值零偏差,波形畸变小。采用式（32）进行三相子模块电容电压均值偏差度计算：

图7 情形1 下3 种方法的MMC 三相子模块电容电压均值一致性测试仿真波形Fig.7 Simulation waveforms of mean consistency test of three-phase submodule capacitor voltages of MMC with three methods in scenario 1

式 中：Vdc,a、Vdc,b、Vdc,c分别为a 相、b 相、c 相子模块电容电压直流偏置量；Vdc,avg为三相子模块电容电压直流偏置量的平均值。

由式（32）计算可得,基于查表法的矢量控制、基于数值解析法的矢量控制与本文方法在t=0.6～0.8 s 期间三相电容电压均值偏差度分别为52.5%、47.5%和10.5%。经量化比较可知,本文方法可实现较优的MMC 三相子模块电容电压均衡一致性控制。

5 基于dSPACE 的实验结果分析

借助dSPACE 平台,建立如附录B 图B1 所示的122 V/750 W MMC 实验系统［24］,验证本文所提基于微分平滑理论的无源一致性控制方法抑制MMC电容电压波动的有效性与可行性。MMC 每相由6 个子模块构成,主电路开关采用SKM50GB123D模块,驱动电路采用SKHI21A 芯片,实验系统参数如附录B 表B1 所示。

5.1 稳态运行条件下电容电压波动抑制实验结果分析

MMC 稳态运行条件下,在t=0.3 s 时,启动本文所提基于微分平滑理论的无源一致性控制方法,进行电容电压波动抑制性能测试,实验波形如图8所示。

网侧三相电压、三相电流实验波形分别如图8（a）和（b）所示。由图8（a）和（b）分析可知,MMC 额定参数下,在t=0.3 s 时启动本文方法,能够保持系统平稳运行；网侧三相电压与电流呈现近似50 Hz 的正弦波形,波形较平滑,谐波小；本文方法采用注入环流方式减少子模块电容电压波动,但未影响网侧电压与电流的电能质量。

a 相上、下桥臂子模块电容电压实验波形如图8（c）所示。由图8（c）分析可知,在t=0.3 s 启动本文方法后,a 相上、下桥臂子模块电容电压明显减小,动态响应快速,超调和稳态误差小,波形畸变率小,保持了较好的对称性和渐近一致性,实现了注入环流期望轨迹渐近跟踪和三相电容电压跟踪同步性的双目标。

a 相环流实验波形如图8（d）所示。由图8（d）分析可知,在t=0.3 s 时,为实现MMC 电容电压波动抑制,注入二倍频环流分量,环流波形经短暂畸变后,幅值稍增加,快速恢复平稳运行,与理论和仿真结果分析一致。

a 相上、下桥臂电流实验波形如图8（e）所示。由图8（e）分析可知,在t=0.3 s 时,a 相上、下桥臂电流由于环流注入而发生畸变,但本文方法以最小的环流注入代价实现了期望的电容电压波动抑制效果,因此能够确保a相桥臂电流发生畸变率尽可能小。

由图8分析可知,稳态运行条件下,本文方法能够快速平抑MMC电容电压波动,动静态响应性能较好。

图8 稳态运行条件下实验波形Fig.8 Experimental waveforms under steady operation condition

5.2 动态运行条件下电容电压波动抑制实验结果分析

为测试本文所提基于微分平滑理论的无源一致性控制方法的稳定性与鲁棒性,在t=0.3 s 时,启动本文方法；在t=0.4 s 时,使直流侧电压由150 V 阶跃上升至额定值的5%,即增至157.5 V,同时使a 相上、下桥臂电阻由0.025 Ω 突增一倍,即增至0.05 Ω,实验波形如图9 所示。

图9 动态运行条件下的实验波形Fig.9 Experimental waveforms under dynamic operation condition

网侧三相电压、三相电流实验波形分别如图9（a）和（b）所示。对比图8（a）和图9（a）、图8（b）和图9（b）可知,在t=0.4 s 时,当直流侧电压突变和a 相桥臂参数摄动同时发生,网侧三相电压波形和网侧三相电流波形依然平滑,能够保持平稳运行。

a 相上、下桥臂子模块电容电压实验波形如图9（c）所示。对比图8（c）和图9（c）可知,在t=0.4 s 时,应用本文方法,能够实现存在外部不确定性扰动情形下,a 相上、下桥臂子模块电容电压经短暂调整后快速收敛至期望轨迹,保持了较好的运行稳定性；本文方法通过实现平滑输出误差渐近为零的控制目标,实现了未建模误差引起控制误差的快速消除,增强了控制系统的鲁棒性。

a 相环流实验波形如图9（d）所示。对比图8（d）和图9（d）可知,在t=0.4 s 时,外部不确定性扰动和内部参数摄动同时发生,环流畸变稍有增大,对称性受到影响,但幅值增大不明显,为维持子模块电容电压平稳,本文方法注入环流代价较小。

a 相上、下桥臂电流实验波形如图9（e）所示。对比图8（e）和图9（e）可知,在t=0.4 s 时,直流侧电压和a 相上桥臂电阻参数突升,a 相环流幅值变化不明显,因而上、下桥臂电流波形与稳态运行条件下类似,未发生明显畸变,a 相上、下桥臂电流经短暂过渡后快速恢复平稳,本文方法能消除外部不确定性扰动和内部参数摄动对闭环控制系统期望轨迹跟踪性能的影响,收敛速度快,稳定性好。

在t=1.6～1.8 s 期间,MMC 三相上桥臂子模块电容电压波形如图9（f）所示,结合图9（f）进行稳态和动态运行条件下a 相子模块电容电压谐波分析,FFT 分析结果如图10 所示,其中纵坐标表示以直流分量为100%计算各谐波幅值。由图9（f）和图10 分析可知,稳态和动态运行条件下,应用本文方法,MMC 电容电压总谐波畸变率（THD）仅为2.29%和2.65%,本文方法对2 次和3 次电容电压谐波抑制效果明显,同时三相电容电压均值保持了较好的一致性,说明将一致性引入无源性控制律对于注入环流参考轨迹跟踪同步性是有益的,验证了理论分析的结果。

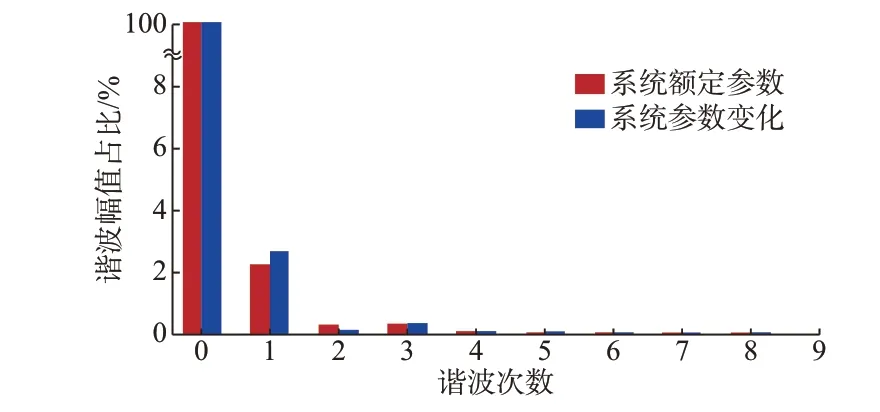
图10 稳态和动态运行条件下MMC 的a 相子模块电容电压FFT 分析Fig.10 FFT analysis of phase-a submodule capacitor voltage of MMC under steady and dynamic operation conditions

6 结语

针对MMC 波动电容电压与注入环流间非线性映射关系解析求取复杂、矢量闭环控制稳定域窄等问题,本文从系统非线性本质出发,应用微分平滑理论,提出了一种形式简单、稳定性好、鲁棒性强、同步性优的无源一致性控制方法。主要结论如下：

1）注入环流期望轨迹的快速准确生成,克服了重复控制方法对不确定性扰动和未建模误差较敏感的不足,同时避免了数值解析法对非线性关系的复杂计算,易于工程应用。

2）基于PCHD 模型,设计了全局渐近稳定的无源性控制律,通过全局能量整形,实现系统内部能量优化利用,提升了MMC 输出能效,仅需较小的注入环流,即可实现MMC 电容电压波动的快速抑制。

3）将一致性控制引入无源性控制律,保持控制器形式简单,计算量小,在注入环流期望轨迹快速跟踪目标实现的同时,完成了三相电容电压均值零偏差目标,实现闭环控制系统双自由度。

本文所提基于微分平滑理论的无源一致性控制方法在单相短路接地情形下的应用是下一步可开展的研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。