恒馏出液组成常规间歇精馏过程模拟的数值计算误差
曾 真,王为国,罗旌崧,覃远航,王存文,赵子傲
1.武汉工程大学机电工程学院,湖北 武汉 430205;2.武汉工程大学化工与制药学院,教育部绿色化学过程教育部重点实验室(武汉工程大学);湖北省新型反应器与绿色化学工艺重点实验室(武汉工程大学),湖北 武汉 430205
模拟是研究间歇精馏过程的重要方法。1902年,Rayleigh首先将数学引入间歇精馏过程的模拟研究,并提出了著名的Rayleigh方程。Rose等[1],Huckaba等[2],Distefano[3-4],Gallun等[5],Sadotomo和Miyahara[6],Cho和Joseph[7]等均对间歇精馏过程的物理模型和计算方法进行了研究,并得到有价值的结果。Galindez等[8]提出了模拟间歇精馏过程的拟稳态法。在化学工程单元操作教程中[9-10],二元间歇精馏过程的物系及过程条件均被理想化,即,其物理模型简化为理想模型。近年来,课题组基于理想模型的模拟(计算)结果,对常规[11-13]、全回流[14-16]和提馏[17-18]等间歇精馏过程的基础理论进行了研究。模拟实际间歇精馏过程时,常用实验结果来检验模拟结果的合理性及优劣。模拟结果与实验结果之间的偏差来源于物理模型误差和数值计算误差,基于理想模型的模拟(计算)结果,难以用实验方法验证其优劣。非稳态间歇精馏过程离散后进行数值计算,截断误差和舍入误差是其固有误差。拟稳态法模拟理想条件下恒馏出物组成(恒顶浓)操作常规二元间歇精馏过程,计算过程总汽化量的程序为嵌套控制结构,即总汽化量的数值结果中含有中间变量计算误差的传播误差,即,其数值计算结果的误差为截断误差、舍入误差和传播误差的耦合。由于舍入误差和传播误差是随机的,对于给定的分离任务,当理论板数有限时,根据大数定律[19],通过对截断误差可以忽略且足够多不同步长(或过程离散段数)的数值计算结果进行算术平均,可计算出与总汽化量真实值充分接近的数值,从而近似计算出总汽化量数值计算结果误差。显然,要近似计算出误差,必须先找出什么条件下截断误差可以忽略。Richardson外推法[20]是估计数值计算结果截断误差的常用方法,当随机的舍入误差和传播误差在误差中显著呈现时,直接用Richardson外推法估计总汽化量数值结果的截断误差,估计结果的稳定性较差,表明估计结果的准确性较差。本文将大数定律与Richardson外推法有机结合,提出通过拟合多组总汽化量的数值计算结果与对应的过程离散数,计算Richardson外推法误差系数的拟合法,有效地降低了(或消除)随机误差(舍入误差和传播误差)对计算误差系数的影响,提高了Richardson外推法估计总汽化量数值结果截断误差的准确(稳定)性,对完善间歇精馏过程的模拟技术有意义。
1 的数值计算方法
1.1 基本方程
假定常规二元间歇精馏过程的理想条件如下:(1)二元混合物是理想的混合物,相对挥发度视为常数。(2)塔内汽相和液相流动为恒摩尔溢流。(3)每一板块均为理论板。(4)再沸器相当于一板理论塔板数。(5)忽略理论板上的持液量和持汽量。(6)塔顶冷凝器中的汽相完全冷凝。(7)忽略塔顶的持液量和持汽量。理想条件下,常规二元间歇精馏过程的基本公式如下:
(1)相平衡方程

式(1)中,x为液相中轻组分摩尔分数,y为汽相中轻组分摩尔分数,α为相对挥发度。
(2)微分物料衡算方程

式(2)和式(3)中,nD为瞬间的馏出物总量(kmol),nW为再沸器内瞬时液相量(kmol),xD为馏出物中轻组分的瞬时摩尔分数,xW为再沸器内液相中轻组分的瞬时摩尔分数。
(3)操作线方程
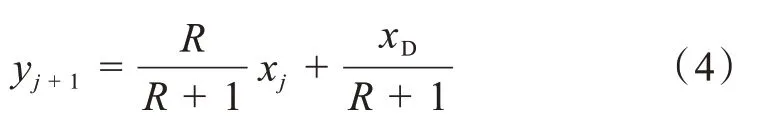
式(4)中,j为个理论塔板序号,右下角标j为第j理论塔板的物理量,R为回流比。
(4)一批物料的物料衡算方程

在式(5)-式(7)之中,nF为一批物料的原料总量(kmol),nDe为一批物料的塔顶产品量(kmol),nWe为一批物料的塔底产品量(kmol),xDP为塔顶产品量中轻组分的摩尔分数,xWe为塔底的产品量中轻组分的摩尔分数。η为塔顶产品量中轻组分的收率。
(5)一批物料的总汽化量

式(8)中,nVT为一批物料的总汽化量(kmol)
1.2 离散方程
常规二元间歇精馏过程是非稳态过程。选择xW为自变量,将由xF变为xWe的xW等段长离散为k段得离散方程如下:

式(9)-式(11)中,k数值计算时过程的离散段数,ΔxW为xW的离散步长,i为离散段序号,右下角标i为第i离散段的物理量,上标“—”为一个离散段物理量的平均。
对每一离散段物料衡算得
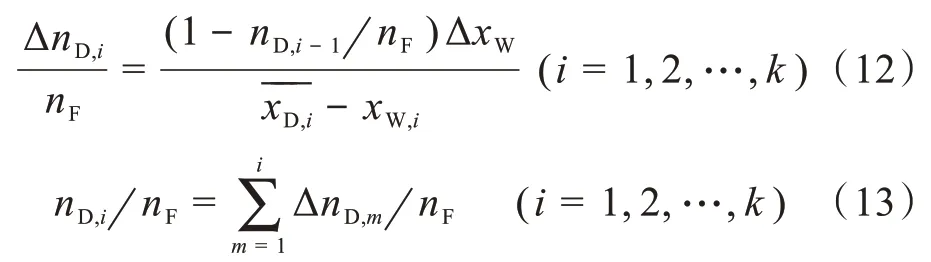
式(12)和式(13)中,nD,i为从开始到第i个离散段结束的馏出物总量(kmol),ΔnD,i为第i个离散段的馏出液量(kmol)。对于恒馏出物组成操作,式(12)中的=xDP(i=1,2,…,k)。
由式(8)得
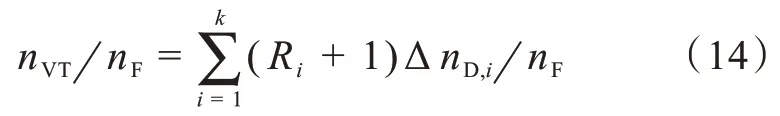
1.3 数值计算的编程步骤
拟稳态法模拟理想条件下恒馏出物组成操作常规二元间歇精馏过程,数值计算的编程步骤如下:
Step1:输入:α、nF、xF、η、xDP、N+1、k和e;
Step3:由 式(9)、(10)和(11)计 算ΔxW,xW,i(i=0,1,…,k)和(i=1,2,…,k);
Step4:由子程序计算Ri(i=1,2,…,k);
Step7:输出计算结果。
主程序中N+1为理论塔板数(包括再沸器),e为数值计算时Ri(i=1,2,…k)规定的收敛精度。
本文将由上述步骤编制的计算程序称为主程序。主程序步骤Step4是使用子程序计算Ri。在子程序中,Ri是采用二分法[21]迭代计算。子程序编程步骤如下:
Step1:由主程序输入:α、N+1、i、xDP和e;
Step2:t=0,赋Ri的初始搜索区间[R(0)i,a,R(0)i,b];

①R(t)i达到收敛精度(ε(t)i≤e),转到Step6;
②R(it)未达到收敛精度(ε(it)>e),当时,和,当时,和,转到Step3;
Step6:Ri=R(t)i,回主程序。
子程序中,t为数值计算过程中子程序的迭代次数,右上角标(t)为数值计算过程中子程序第t次迭代的物理量,εi为Ri(i=1,2,…k)数值计算结果的相对残差。
1.4 计算程序验证
由文献[22]可知,在理想条件下,当N+1→∞时可由式(15)解析计算。
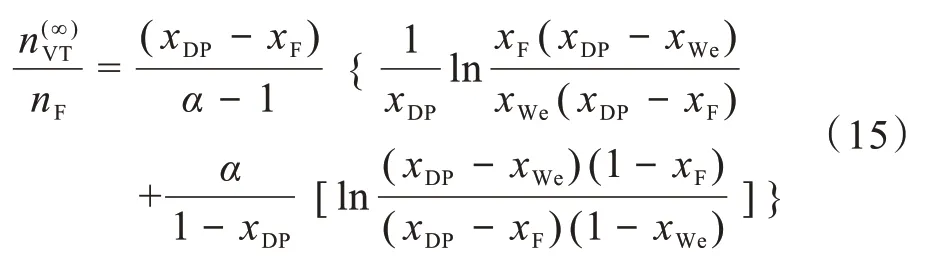
式(15)中,右上角标(∞)为N+1→∞时的物理量。
对于给定的分离任务,随着N+1增大,向渐近。为了验证计算程序,给定的分离任务Ⅰ(α=2.500 000 ,xF=0.400000 0,η=0.900 000 0,xDP=0.960 000 0)和分离任务Ⅱ(α=2.500 000 ,xF=0.700 000 0,η=0.800 000 0,xDP=0.9000000)。对于分离任务Ⅰ,由式(5)、(6)和(7)得xWe=0.064 000 0,由 式(15)得=1.486 198[右上角标(a)为解析计算结果]。对于分离任务Ⅱ,由式(5)、(6)和(7)得xWe=0.370 5882,由式(15)得1.013255。
图1显示,对于2个分离任务,随着N+1增大[右上角标(n)为数值计算结果]均向=1.013255渐近,表明的计算程序是正确的。本文中称上述验证计算程序的方法为渐近法。
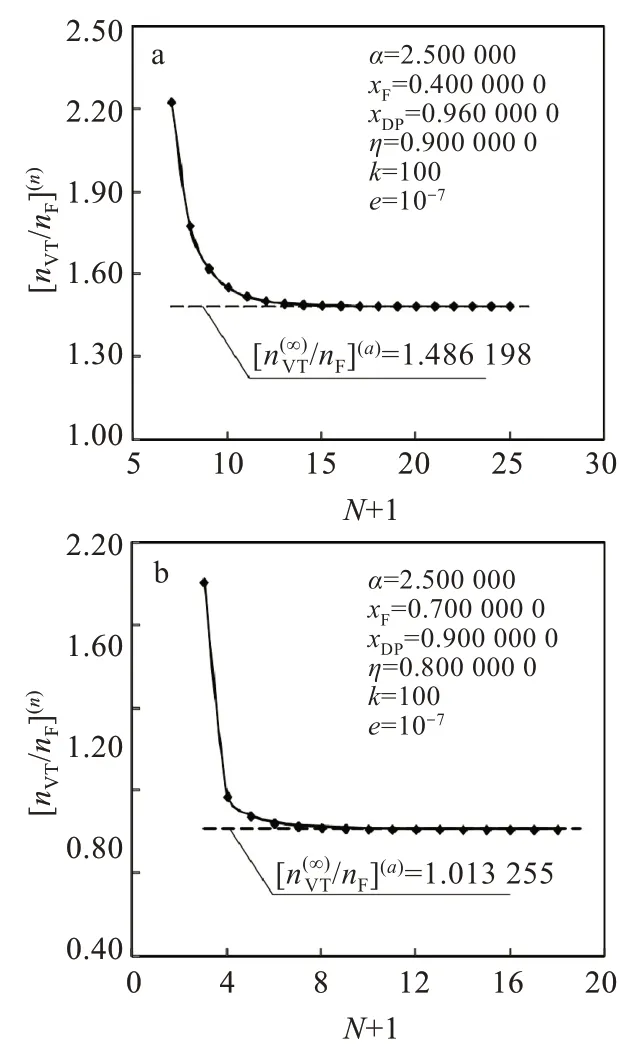
图1 理论塔板数对总汽化量的影响:(a)分离任务Ⅰ,(b)分离任务ⅡFig.1 Effect of number of theoretical plates on total vaporization:(a)separation task I,(b)separation task II
1.5 的数值计算方法
文献[12]中图1显示,对于常规二元间歇精馏过程,当N+1→∞时,x(∞)D可表示为:

在 式(16)中,R(∞)C=1/[(α-1)xW],为N+1→∞时,塔顶和塔底同时为恒浓度区的回流比。
在恒馏出物组成操作常规二元间歇精馏过程中,xD=xDP≤1,R≤R(∞)C。因此,当N+1→∞时,其瞬时回流比为

过程离散化后,由式(17)得到每一离散段的回流比为:
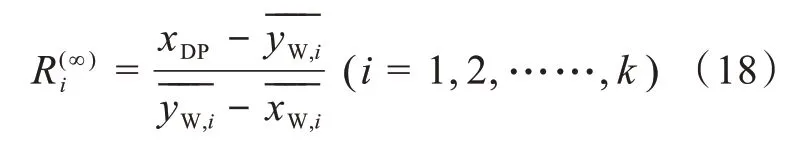
图2 过程的离散段数与总汽化量数值计算结果的关系:(a)分离任务Ⅰ,(b)分离任务ⅡFig.2 Relationship between number of discrete segments of process and numerical calculation results of total vaporization:(a)separation task I,(b)separation task II
2 [](n)的计算误差分析
非稳态间歇精馏过程离散后进行数值计算,截断误差Et和舍入误差Er是其固有误差。拟稳态法模拟理想条件下恒馏出物组成操作常规二元间歇精馏过程,数值计算的程序为嵌套控制结构,在的误差E中,应包括来自R(n)i(i=1,2,…k)计算误差的传播误差Ep,则
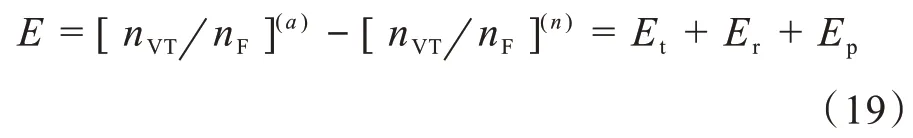
式(19)中,E为的 误 差,Er为的舍入误差,Et为的截断误差,Ep为来源于R(n)i(i=1,2,…k)数值计算误差传播引起的计算误差(传播误差)。
2.1 [](n)的误差E
对于一定分离任务,当N+1→∞时,可由式(15)解析计算,误差E可由式(19)计算。当N+1有限时,不能准确计算出的真实值,因此,不能直接由式(19)计算准确计算出的误差E(n)。由于Er与Ep是随机的,当截断误差Et很小,可以忽略时,根据大数定律[19],通过对足够多不同步长(或过程离散段数)的进行算术平均,可数值计算出与充分接近的数值从而近似计算出与总汽化量数值计算结果的E(n)真实值充分接近的数值。举例验证和应用如下:
(1)对于分离任务I,N+1→∞时,由图2(a)可见,k≥1 000,围绕波动,表示截断误差很小,可以忽略。由图4(a)可见,C(∞),(f)k=0.389 4[右上角标(f)为拟合计算结 果]。k=1 000时,由 式(24)可 得,E(∞)t≈E(∞),(f)t=3.894×10-7。k=1 000-2 000时 ,,本文使用的计算软件是32 bit系统,数值计算结果为7位有效数),当N+1→∞和k=100时,数值计算 得,=1.486159,则,由 式(19)得则 其 相 对 误 差
(2)对于分离任务Ⅱ,N+1→∞时,由图2(b)可见,k≥1 000,围绕波动,表示截断误差很小,可以忽略。由图4(b)可见,C(∞),(f)k=-0.111 1。k=1 000时,由式(24)可得,E(∞)t≈E(∞),(f)t=-1.111×10-7。由 图2(b)可见 ,k=1 000-2 000时 ,1.013255=。当N+1→∞和k=100时,=1.013266,则,由 式(19)得=-1.1×10-5。则 其 相 对 误 差
(3)对于分离任务I,当N+1=13和e=10-7时,由图3(a)可见,k≥1000,围绕波动,表示截断误差很小,可以忽略。由图5(a)可见,C(f)k=0.3930。则,k=1000时,由 式(24)可 得,E(n)t≈E(f)t=3.930×10-7。k=1000-2 000 时 ,1.496 075。当N+1=13、e=10-7和k=100时,数值得,=1.496 035,由式(19)得,E(n)≈=4.0×10-5。相对误差2.7×10-5。
(4)对于分离任务Ⅱ,当N+1=8和e=10-7时,由图3(b)可见,k≥1000,围绕波动,表示截断误差很小,可以忽略。由图5(b)可见,C(f)k=-0.112 6。则,k=1000时,由式(24)可得,E(n)t≈E(f)t=-1.126×10-7。k=1000-2000时,1.021 851。当N+1=8、e=10-7和k=100时,数值计算得,=1.021862,由式(19)得,E(n)≈=-1.1×10-5。则其相对误差
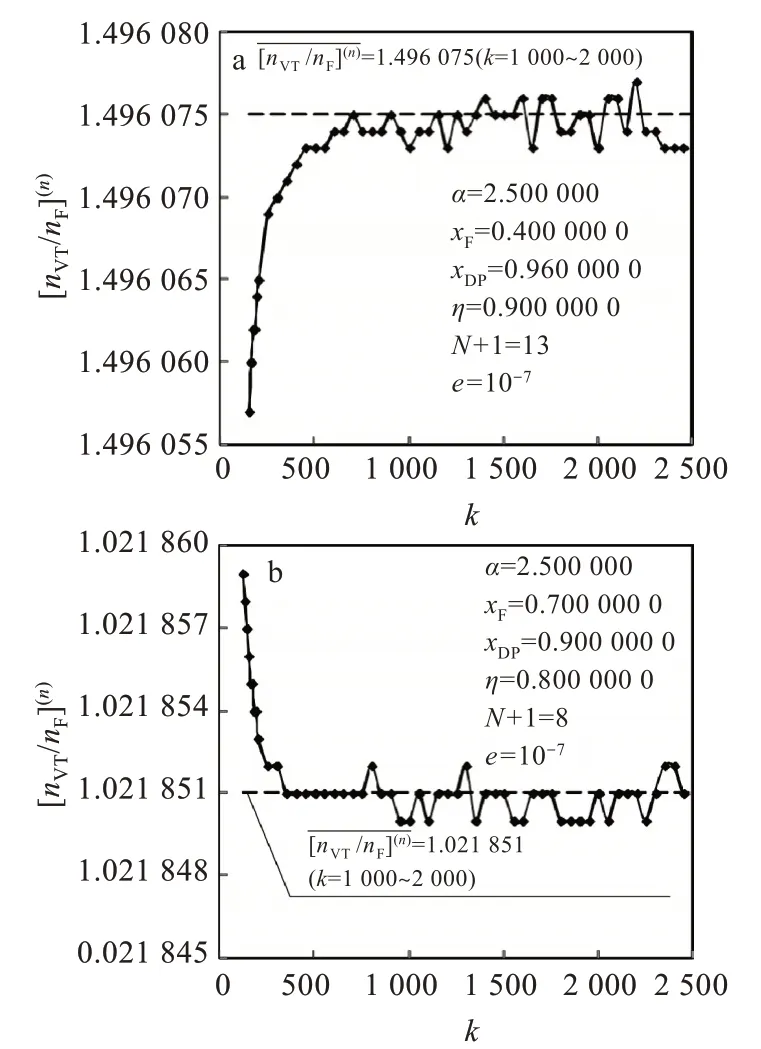
图3 总汽化量数值计算结果与过程离散段数的关系(a)分离任务Ⅰ,(b)分离任务ⅡFig.3 Relationship between numerical calculation results of total vaporization and number of discrete segments of process:(a)separation task I,(b)separation task II
例(1)和(2)为验证,例(3)和(4)为应用,因此,在截断误差可以忽略的条件下,可根据大数定律,对总汽化量数值计算结果的误差进行定量描述,可为“模拟间歇精馏过程的数值计算误差非常小”提供的定量证据。
2.2 [n VT n F](n)的传播误差Ep
由式(14)可见,R(n)i(i=1,2,…k)的计算误差可 直 接 传 播 到。 当εi=0(i=1,2,……,k)时,Ep=0。设R(ε=0)i(i=1,2,…,k)和为 对 应 于εi=0(i=1,2,……,k)的数值计算结果。由式(14)和(19)可得
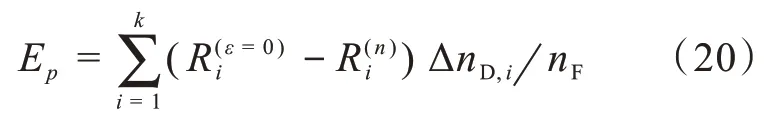

式(21)代入(20)得
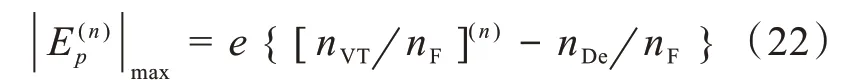
2.3 [](n)的舍入误差E r
当k不是非常大时,Er很小,可以忽略。在数学上,舍入误差量化估计是仍然需要研究的问题,基于本文数值计算结果,和的舍入误差量化估计举例如下:
(1)当N+1→∞时,R(∞)i由式(18)解析计算,因 此,的 总 计 算 误 差E(∞),(n)中,E(∞),(n)p=0。对于分离任务I,由图2(a)可见,k=1000-2 000范围内,k=1 900时,|E(∞),(n)|最大。当k=1 900时,数 值 计 算 得1.486 201,由式(19)得,|E(∞),(n)|=3×10-6。由图4(a)可 见,=0.389 4,由 式(24)可 得,由 式 (19) 可 得。假定舍入误差正比于离散段数,则,k=100时, ||E(∞),(n)rmax在10-7数量级。
(2)对于分离任务I,当N+1=13和e=10-7时,k=1000-2 000范围内,k=1000时,||最大。当k=1000时,数值计算得1.496 072,由式(19)得。由图5(a)可 见 ,C(f)k=0.3930,由 式(24)可 得 ,=3.930×10-7,由式(22)得,|Ep|max=1.121×10-7,由式(19)可得≈4×10-6。假定舍入误差正比于离散段数,则,k=100时在10-7数量级。
2.4 [n VT n F](n)的截断误差Et
由图2和图3可见,对于两个分离任务,当k较小时和是的单调函数,表明截断误差Et在计算误差E中占主导地位,当k较大时和不再是的单调函数,表明截断误差不再占主导地位,随机的舍入误差和传播误差在误差中显著呈现,当k很大时,围绕波动围绕波动,表示截断误差不显著呈现。
2.4.1 拟合法计算Richardson外推法误差系数的提出Richardson外推法是一种常用的截断误差估计方法[20],Richardson外推法是利用Taylor级数进行分析,用于截断误差估计时,在渐近线范围内常常只保留幂级数的首项。即

在式(23)中,C是与ΔxW无关的常数,O是高阶无穷小,p为计算方法的收敛精度阶,是Taylor级数首项的幂,一般为正整数。离散步长与离散段数成反比,因此,可以将式(23)变为

式(24)中,Ck为计算截断误差的系数(本文简称误差系数)。由式(24)可见,略去式(24)中高阶无穷小,如果确定了p和Ck,可计算出Et与k的数值关系。将式(24)代入式(19)得

对于两个分离任务,当e=10-7和k=100时,由2.3可知在10-7数量级,由2.2可知,在10-7数量级。结合由图2、图3与式(25)可 得,当k=100时,|E|>> |Ep|和 |E|>> |Er|Et≈E。由式(24)与(25)可见,忽略高阶无穷小Ok、舍入误差和传播误差的影响,当N+1→∞时,可 由 式(15)解 析 计 算,由 两 组和相应的k可确定p和C(∞)k。当N+1有限时,仅能计算出与真实值充分接近的数值在未知情况下,由三组和相应的k可确定p和Ck。
当随机的舍入误差和传播误差在误差中显著呈现,忽略舍入误差和传播误差的影响,直接由式(25)计算误差系数Ck,计算结果的稳定较差,即,直接用Richardson外推法估计总汽化量数值结果的截断误差,估计结果的稳定性较差。目前,在数学上,提高估计截断误差准确(稳定)性的方法是保留Taylor级数更多项数(采用更多组不同步长的数值计算结果),课题组前期研究表明,计算误差系数方法是解线性方程组,保留项数越多,计算过程越复杂,即保留项数是有限的,而有限项保留不能显著地提高截断误差估计结果的稳定性。根据的大数定律,本文认为拟合足够多组和相应的k来计算Richardson外推法的Ck,可以有效地降低(或消除)Er和Ep对计算Ck的影响,可较为准确地估计Et。
2.4.2 拟合法计算Richardson外推法误差系数Ck的验证数值计算方法的收敛精度阶p为Taylor级数首项的幂,一般为整数。在拟合和对应的k前,对p进行整数预设,拟合过程和结果可在Microsoft Excel电子表格上呈现。如果预设的p正确,拟合估计法合理,在 |E|>> |Ep|和条件下,由式(25)可见与k-p必定呈良好的线性关系(Microsoft Excel电子表格拟合的线性相关系数接近1),由式(19)和(24)可见必定成立。
由图4可见,对于2个分离任务,当k=40-150时,采用Microsoft Excel电子表格拟合和k-2的线性相关系数均接近1,表明拟稳态法数值计算具有二阶收敛精度。
对于两个分离任务,E(∞),(n)p=0,由2.3可知,k=100时在10-7数量级。对于分离任务I,当N+1→∞和k=100时,由图2(a)可见,E(∞),(n)=3.9×10-5,即 ,和因此,≈3.9×10-5。由图 4(a)可 见 ,C(∞),(f)k=0.389 4,则 ,。对 于 分 离 任 务Ⅱ,当N+1→∞和k=100时,由图2(b)可见,E(∞),(n)=-1.1×10-5,即和因 此≈-1.1×10-5。由图4(b)可见,C(∞),(f)k=0.111 1,则1.01。因此,当N+1→∞时,拟合法计算Richardson外推法的误差系数C(∞),(f)k,可较为准确地定量估计E(∞)t。

图4 采用Microsoft Excel电子表格拟合总汽化量数值计算结果与过程离散段数:(a)分离任务Ⅰ,(b)分离任务ⅡFig.4 Fitting of numerical calculation results of total vaporization and number of discrete segments of process by using Microsoft Excel spreadsheet:(a)separation task I,(b)separation task II
对于两个分离任务,当e=10-7和k=100时,由2.3可知在10-7数量级,由2.2可知,在10-7数量级。对于分离任务I,当N+1=13、e=10-7和k=100时,10-5,即,和,因 此,E(n)t≈4.0×10-5。由图5(a)可见,当N+1=13时,C(f)k=0.3930,C(f)kk-2=3.930×10-5,即,≈0.98。对于分离任务Ⅱ,当N+1=8、e=10-7和k=100时,E(n)≈=-1.1×10-5,即 ,和,因 此 ,E(n)t≈-1.1×10-5。由图5(b)可见,当N+1=8时,C(f)k=-0.112 6,C(f)k k-2=-1.126×10-5,即,≈1.02。因此,拟合法计算截断误差Richardson外推法的误差系数Ck,可较为准确地定量估计Et。
此外,对于分离任务Ⅱ,由图5(b)可见,N+1=8时C(f)k是负值,由图5(c)可见,N+1=3时C(f)k是正值,表明Et的方向有可以随N+1变化。
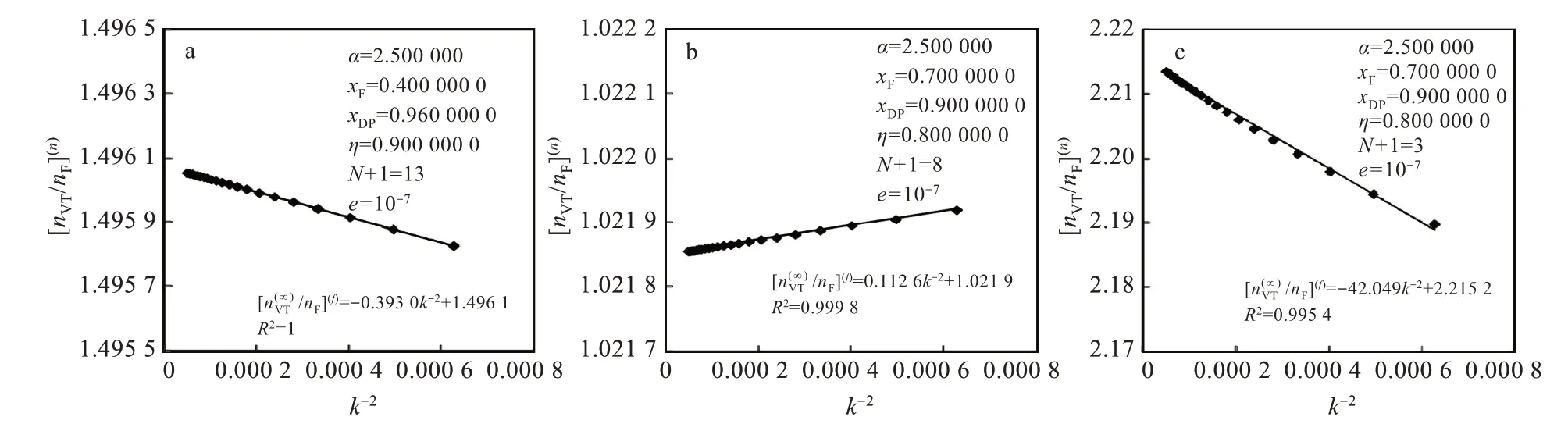
图5 采用Microsoft Excel电子表格拟合总汽化量数值计算结果与过程离散段数示例:(a)分离任务Ⅰ,N+1=13,(b)分离任务Ⅱ,N+1=8,(c)分离任务Ⅱ,N+1=3Fig.5 Examples of fitting of numerical calculation results of total vaporization and number of discrete segments of process by using Microsoft Excel spreadsheet:(a)N+1=13 for separation taskⅠ,(b)N+1=8 for separation taskⅡ,(c)N+1=3 for separation taskⅡ
2.4.3 拟合法计算Richardson外推法误差系数Ck的应用举例对于恒馏出物组成操作常规二元间歇精馏,由Fenske方程[22]知,过程结束时所需的最少理论达到其最大值,此最大值为所需的最少理论塔板数,即

由式(26),对于分离任务Ⅰ,Nmin+1=6.260899,对于分离任务Ⅱ,Nmin+1=2.976041。
图6显示N+1对C(f)k的影响。对于分离任务Ⅰ,当N+1=7时,C(f)k=3.321 2(未示出),对于分离任务Ⅱ,当N+1=3时,C(f)k=42.049,[未示出,见图5(c)]。由图6可见,对于两个分离任务,①当N+1≥2(Nmin+1)时,C(f)k≈C(∞),(f)k,表明当理论板较大(大于2倍所需的最少理论板)时,Et与相同过程离散段数的E(∞)t相当。②当N+1≥3(Nmin+1)时,C(f)k围绕C(∞),(f)k波动,表明有限组和k拟合,随机的Er和Ep对拟合结果仍有影响。
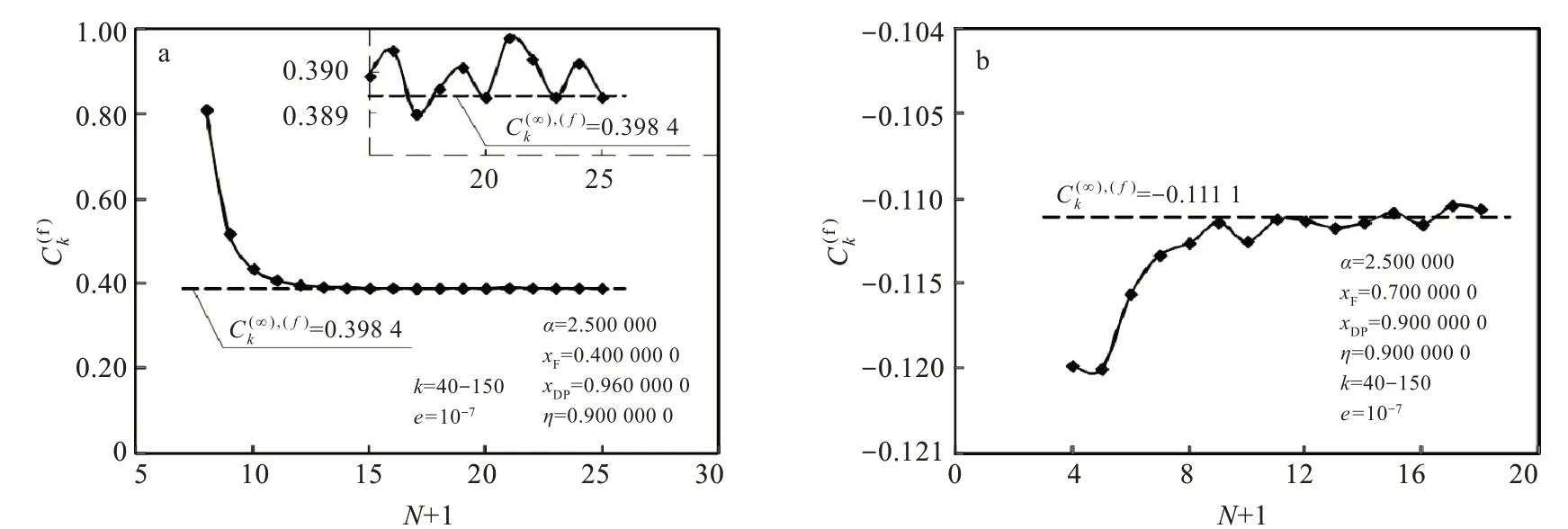
图6 理论塔板数对误差系数的影响(a)分离任务Ⅰ,(b)分离任务ⅡFig.6 Effect of number of theoretical plates on error coefficient:(a)separation taskⅠ,(b)separation taskⅡ
3 结 论
(1)根据大数定律,提出了N+1有限时,误差的近似计算方法,并举例验证和应用。误差的近似计算方法为:在的截断误差可以忽略的条件下,通过对足够多不同步长(或过程离散进行算术平均,计算出与真实值充分接近的数值再由式(19)计算出与误差真实值充分接近的数值。
(2)根据大数定律,提出了采用拟合法计算Richardson外推法的误差系数Ck。拟合法通过拟合足够多组和对应的k计算Ck,有效降低了(或消除)随机误差(舍入误差和传播误差)对计算Ck的影响,提高了Richardson外推法估计截断误差的准确(稳定)性。通过举例对拟合法进行验证和应用,并得到结论如下:①拟稳态法模拟理想条件下,恒馏出物组成操作常规二元间歇精馏过程,具有二阶收敛精度。②拟合法计算Ck时,对p进行整数预设,拟合过程和结果可在Microsoft Excel电子表格上呈现。
(3)通过举例,对模拟理想条件下恒馏出物组成操作常规二元间歇精馏过程的和的数值计算结果的截断误差进行讨论,得到结论如下:当N+1≥2(Nmin+1)时,C(f)k≈C(∞),(f)k,表明当理论板较大(大于2倍所需的最少理论板)时,Et与相同过程离散段数的E(∞)t相当。

