围压、温度及损伤程度对隧道围岩渗透率的影响

朱 亮

(中铁十九局集团第一工程有限公司，辽宁 辽阳 111000)

0 引言

深部岩石通常处于“三高一扰动”的复杂应力环境中。“三高”指高地应力、高温和高孔隙水压，“一扰动”指开挖破坏了原岩的应力环境，产生应力重分布，进而对原岩造成初始损伤。文章结合辽宁某在建隧道的实际情况，对该隧道砂岩在高温、高地应力及扰动状态下围岩的渗透性进行研究。

近年来，我国学者对岩石渗透率方面的研究成果颇丰。张磊等[1]针对采煤过程中瓦斯渗透问题，通过循环加载试验对完整煤样和裂隙煤样分别进行了渗透性试验研究。李治豪等[2]基于COMSOL数值计算方法对不同粗糙度的岩石进行了渗透性试验研究，监测了试验过程中气体流量及裂隙内部应力的变化情况。张宏学等[3]通过现场试验与室内试验相结合的方法，对气体解吸导致的页岩储气层渗透率改变进行了研究。郤保平等[4]通过压力脉冲衰减法对高温处理后的花岗岩的渗透性进行了试验研究，分析了花岗岩不同物理力学参数受温度影响情况。张玉等[5]针对油气储存在深部围岩内的运移问题，对裂隙岩石展开了复杂应力路径下的渗透性试验。王磊等[6]为了获得水蒸气在不同温度下对页岩的渗透率的影响规律，对高温处理后的水蒸气对页岩渗透率及页岩各向异性的影响进行了室内试验研究。王彪等[7]以巴郎山隧道工程为背景，对不同围压下该隧道围岩进行了气体渗透性试验研究，以此对该隧道围岩的安全稳定性进行评价。张亮等[8]针对裂隙煤岩的渗透性问题，对不同实际工况下煤岩的动态导流性能及裂隙煤岩的渗透率进行了现场测试分析。赵静等[9]针对原位油页岩在高温条件下的渗透性问题，采用高温高压三轴试验系统及气体渗透试验系统对该页岩进行了渗透率试验研究，揭示了高温高压下油页岩的渗透演化规律。侯宜峰等[10]采用室内三轴试验系统对加载破坏过程中岩石的气体渗透规律进行了研究，分析了渗透率与应变之间的关系。

综上分析，已有成果对岩石渗透率进行了较为详细的研究，但对应力、温度及损伤三项耦合方面的研究相对较少。本文在总结已有研究成果的基础上，对辽宁某在建隧道砂岩进行了渗透率室内试验研究，综合考虑了应力、温度及损伤程度对岩石渗透率的影响。研究成果能够对工程实际提供一定程度的指导意义。

1 试验介绍

1.1 试样制备

本文试验用岩样采自辽宁某在建隧道砂岩，为了确保试样均一性，所有试验用岩样均取自同一完整岩块。经现场粗加工后运抵至室内试验室，经切割、钻孔、打磨等工序后，最终制得直径50 mm、高100 mm的标准圆柱试样。

为了研究该隧道砂岩的渗透特性，需对试样的孔隙率进行测量。首先，取3个岩样放入真空饱水容器中进行24 h饱水处理，时间达到后每隔20 min对试样进行一次质量记录，直至连续3次质量误差在0.5%以内时可认为试样达到饱和。然后将饱和后的试样置于烘干仪中，2 h后测量试样质量，直至连续3次质量误差在0.5%以内时可认为达到干燥状态。最后根据饱水法计算本文砂岩孔隙率为5.63%。

为了得到不同损伤程度的砂岩试样，本文采用峰前卸荷的方式使试样具有损伤性质。首先对试样进行单轴压缩试验，获取试样的抗压强度，然后根据单轴抗压强度来确定卸荷点。本文取砂岩峰前卸荷点峰值强度分别为30%、60%、90%，以此来获取不同损伤程度的试样。

1.2 试验设备与试验方案

本文不同温度及不同损伤程度的砂岩三轴加载试验均在GCTSRTX-4000高温高压岩石试验系统上完成，渗透试验均在全自动岩石气体渗透系统上完成。为了得到不同试验条件下砂岩的渗透率，采用下式进行计算：

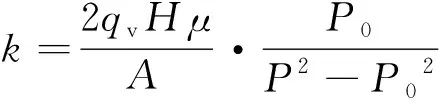
(1)

式中：k为试样的气体渗透率，m2；qv为出口端的气体流量，m3/s；μ为氮气黏度，Pa·s；P为进气段压力，MPa，通常取2 MPa；P0为标准大气压，取0.1 MPa；A为试样的横截面积，m2；H为试样高度，m。

为了定量表示本文砂岩的损伤程度，可通过下式来计算不同卸荷点处的损伤变量[11]：

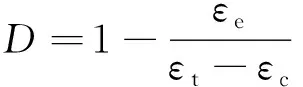
(2)

式中：D为损伤变量；εe为卸荷点处试样的弹性应变；εt为卸荷点处试样总应变；εc为卸荷点处试样的压密应变。

表1为不同温度及不同损伤程度下砂岩的三轴加载试验方案。具体试验过程如下：(1)首先在GCTS RTX-4000试验仪上对试样进行加载，当加载至指定卸荷点时卸载，以此来得到不同损伤程度的岩样。(2)将不同损伤程度的岩样放入气体渗透试验系统中，对试样施加围压，待围压达到预定值后对试样施加不同温度，温度可通过水浴箱进行控制，待温度达到预定值后，恒温2 h。打开进气阀，施加进口端气压(P=2 MPa)，并保持恒定，记录气体流量变化值qv。不同温度下氮气的气体黏度μ不同，可通过查氮气物理性质表得到。将气体渗透试验得到的数据代入式(1)便可得到不同温度、不同损伤程度下砂岩的渗透率。

表1 试验方案

2 试验结果分析

2.1 应力-应变曲线分析

渗透试验开始前，首先对完整砂岩试样进行两次单轴压缩试验，目的是为了检验本文砂岩是否具有较好的一致性。图1为砂岩单轴压缩全过程应力-应变曲线，可以看出，两个试样的应力-应变曲线的变化趋势基本一致，表现为显著的脆性破坏模式。根据单轴压缩试验数据计算本文砂岩的平均抗压强度为55.27 MPa、弹性模量为6.77 GPa、泊松比为0.384，三参数的离散度分别为0.47%、0.52%和2.85%，离散度相对较小，再次验证了本文砂岩的均一性。

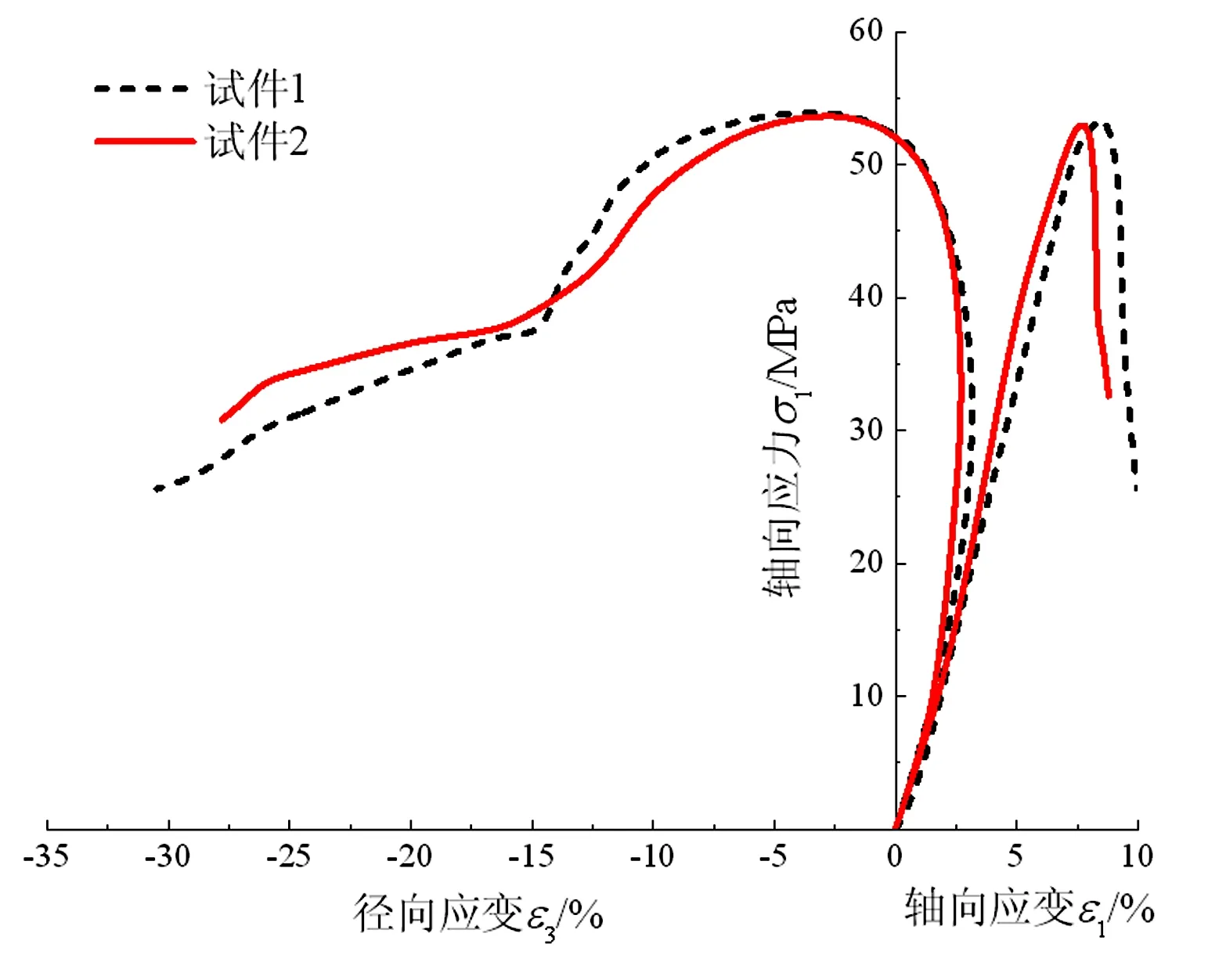
图1 单轴压缩应力-应变曲线

图2为砂岩不同卸荷点应力-应变曲线。由图可知，峰前卸荷均产生了不可恢复塑性变形，且卸荷应力越大，塑性变形越大，对试样产生的损伤程度越严重，损伤变量越大。根据图2及文献[11]，并结合式(2)计算30%、60%、90%的卸荷点的损伤变量分别为0.289、0.297、0.325，再次验证了前述观点。

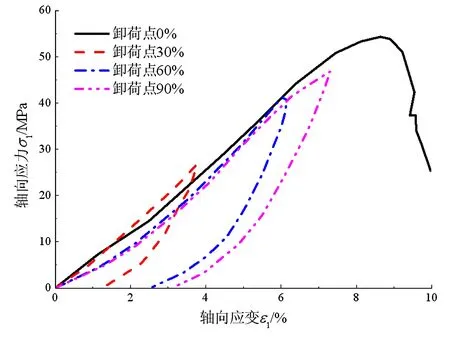
图2 不同卸荷点应力-应变曲线

2.2 围压对渗透特性的影响分析

图3为砂岩渗透率随围压的分布曲线。从图3可以看出，不同温度、不同损伤程度下试样的渗透率随围压的变化曲线基本一致，随着围压的逐渐增大，试样的渗透率均逐渐减小，且不同试验条件下的曲线均呈逐渐趋缓的变化趋势，说明渗透率与围压之间表现为负相关关系。原因是围压越大，试样内部被挤密压缩程度越大，气体渗透通道越窄，从而导致渗透率降低。对比分析不同损伤程度下的渗透率随围压的分布曲线可知，试样的损伤程度越严重，曲线斜率的变化幅度越大。原因是损伤导致试样内部孔隙率增大，内部颗粒骨架结构相对松散，围压5 MPa时试样内部仍留有大量孔隙，气体渗透通畅，渗透率较大；围压10 MPa时试样内部颗粒骨架结构被迅速挤压密实，孔隙率迅速减小，从而导致渗透率快速下降；此后，试样内部孔隙被挤压密实的速率开始减缓，孔隙率的减小速率同样放慢，最终导致渗透率下降速率趋缓。

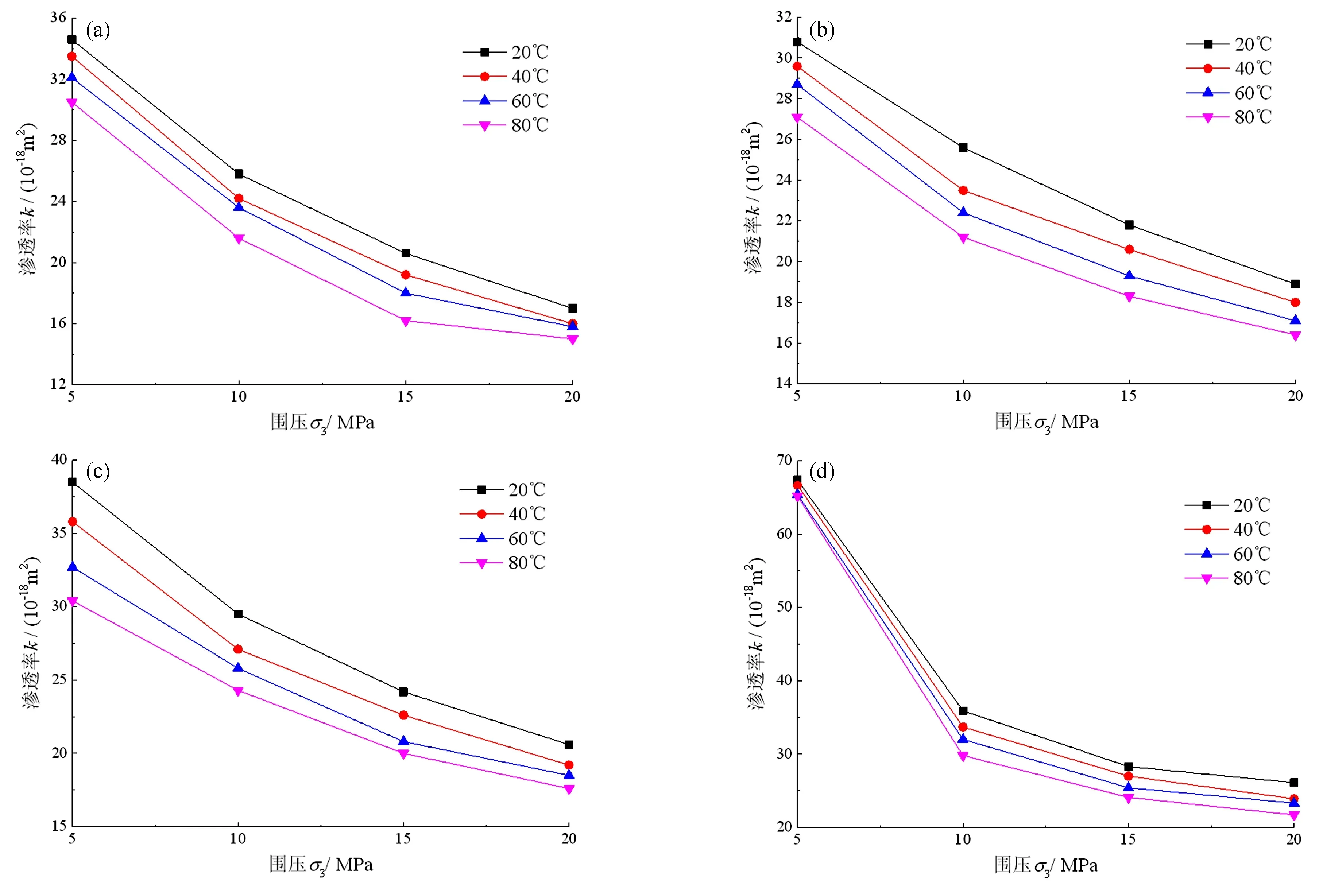
图3 渗透率与围压的关系

2.3 温度对渗透特性的影响分析

图4为砂岩渗透率随温度分布曲线。从图4可以看出，不同围压、不同损伤程度下试样的渗透率随温度的变化曲线基本一致，随着温度的逐渐升高，试样的渗透率呈逐渐递减趋势，说明砂岩渗透率与温度之间满足负相关关系。原因主要是试样内部颗粒在高温作用下发生熔融，加速了试样的腐蚀进程，自由接触面增大，随着温度的升高，试样内部一些成分开始膨胀，孔隙在膨胀作用下被逐渐挤密，气体通道变窄，从而导致孔隙率下降。对比分析不同损伤程度下试样的孔隙率可知，随着损伤程度的逐渐加重，试样渗透率的下降速率逐渐趋缓。原因是损伤程度的加重使得试样内部孔隙开度增大，即使温度的升高在一定程度上降低了裂隙开度，但对于损伤程度较为严重的试样来说，膨胀导致的开度降低对渗透率的影响远低于损伤程度造成的影响。

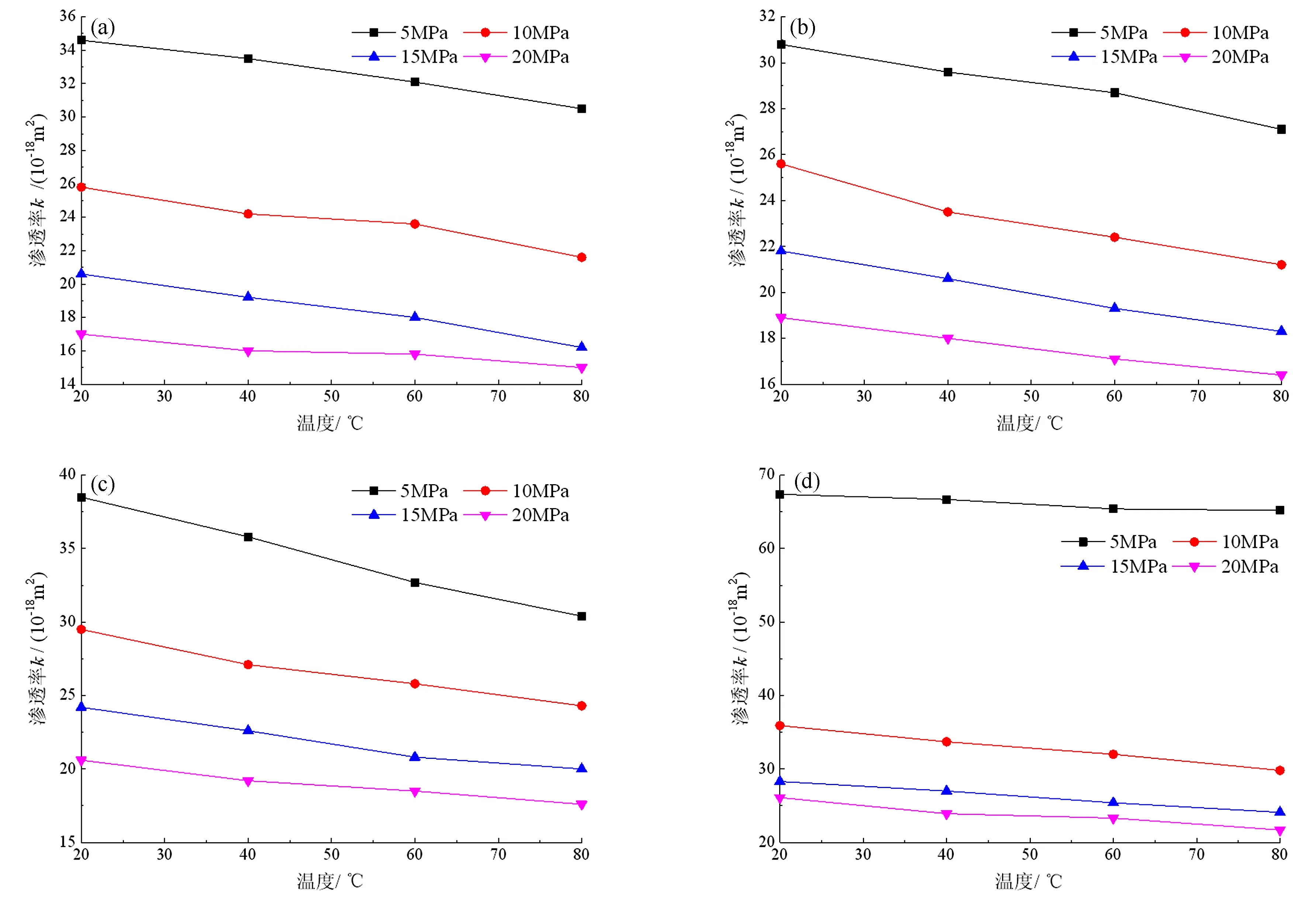
图4 渗透率与温度的关系

2.4 损伤程度对渗透特性的影响分析

图5为砂岩渗透率随损伤变量的分布曲线。从图5可以看出，随着损伤变量的逐渐增大，试样的渗透率呈逐渐递增趋势，其中，低围压(5 MPa)下，试样渗透率随损伤变量先略有降低后再逐渐增大。原因是卸荷点不同对试样产生的损伤程度不同，试样内部出现的孔隙数量也不同，卸荷点为30%峰值强度、损伤变量为0.289时，此时试样内部产生的孔隙数量最少，裂隙发育不显著，且加载初期的压密阶段使试样内部原始孔隙更加紧密，从而导致渗透率出现略微下降情况。卸荷点为60%、90%峰值强度时，损伤变量分别为0.297和0.325，试样损伤程度增大，试样内部孔隙数量增多，裂隙发育显著，导致渗透率逐渐增大。对比分析不同围压及不同温度下砂岩的渗透率随损伤变量的变化曲线可知，围压越低，试样损伤程度越严重，渗透率差异越大。原因是砂岩内部孔隙随着围压的升高而逐渐减少，试样的密实程度逐渐升高，进而使得试样的各向异性逐渐减小。

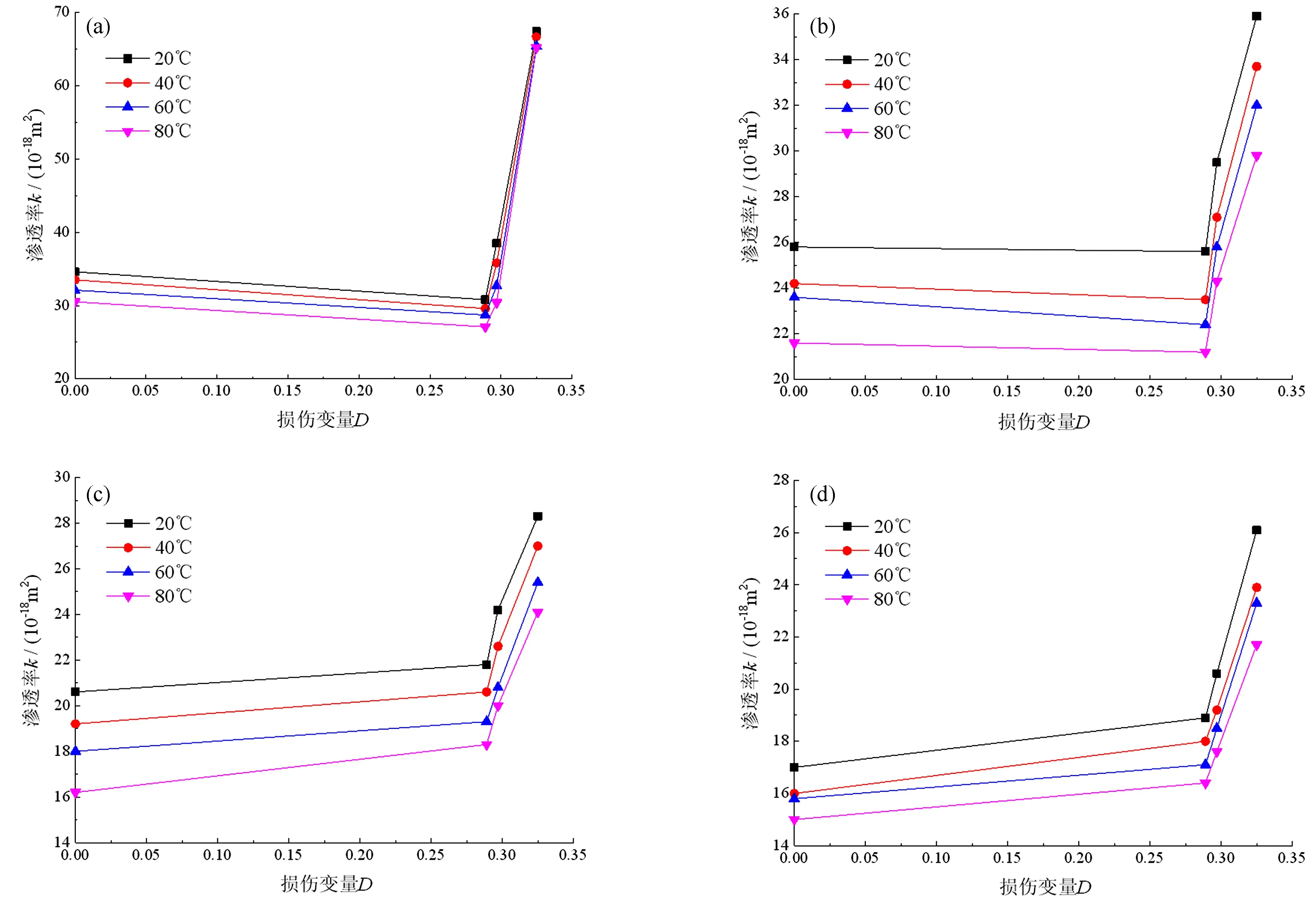
图5 渗透率与损伤变量的关系

3 结论

(1)不同温度及不同损伤程度下，砂岩的渗透率随围压的变化曲线基本相同，随着围压的逐渐增大，砂岩的渗透率呈逐渐递减趋势，表明渗透率与围压之间表现为负相关关系。

(2)不同围压及不同损伤程度下，砂岩的渗透率随温度的变化曲线基本一致，随着温度的逐渐升高，砂岩的渗透率呈逐渐递减趋势，表明渗透率与温度之间满足负相关关系。

(3)不同围岩及不同温度条件下，砂岩的渗透率随损伤变量的变化曲线基本一致，随着损伤变量的逐渐增大，试样的渗透率呈逐渐递增趋势；围压较低条件下，渗透率随损伤变量呈先减后增的变化规律。