基于蚁群算法的二维场地土石方运输路径优化研究

许辉

（中交一公局集团华中工程有限公司，湖北武汉 430014）

0. 引言

传统基建行业成本高、利润薄、工期紧张，通过合理的手段进行设计优化、方案深化比选是工程建设必须考虑的问题。作为建筑施工项目的一个重要方面，在大型工程建设中土石方调配费用占工程建安费比例很高。但土石方运输作为土石方调配中的一个重要步骤，目前却缺乏有效的针对土石方运输路径的研究。因此如何合理的规划土石方运输路径，使其在满足施工现场要求的前提下距离最短，施工成本最低是有必要的。

从20世纪70年代开始，国内外学者就对线路选型，最短路径搜寻展开了研究。孙兴等通过对GIS系统进行二次开发，建立土石方调运系统，实现了调配过程及结果输出的实时动态显示，但其对于调配路径的优化研究较少。黄丙湖等以总成本最小为目标函数建立模型，综合考虑施工次序、方向和调配的土石方量，利用蚁群算法将模型转化为求解最短路径问题，但其调配的基本思路还是基于一维蚁群算法的TSP问题，并没有考虑运输路线中存在的障碍物。缪鹍等基于蚁群算法研究了道路的纵断面曲线，建立了离散的纵断面曲线优化算法模型，但这种方式计算速度慢，对于复杂地形情况下容易产生局部收敛的现象。

针对上述文献中前人研究的成果，本文提出一种考虑障碍物条件的二维路径优化问题，目标是在全局条件下绕过地形图中设置的障碍物，自动搜寻一条最短的运输路径。以荔玉高速21分部1#取土场土石方运输为算例，首先构建二维无向网络图，然后通过Dijkstra算法进行运输路径的初始规划，最后利用蚁群算法在初始规划找寻的节点间进行二次优化得到最终的全局最优路径。

1. 初始路径规划研究

工程建设是一项系统性的、群策群力的活动，每一个环节都串联着诸多行业，其中，物料运输扮演着关键的角色。对于场地活动范围大、工程量大的施工项目，运输用的施工车辆往往占整体施工机械很大比例，这种现象在复杂场地条件下表现的尤为明显。运输距离的长短、运输速度的快慢不仅影响施工成本，对施工工期也会造成一定的影响。因此，有必要在确定施工场地后规划出若干条最优的运输路线，缩短运输车辆行驶的距离，达到降低施工成本，提高施工进度的目的。本文在MATLAB中构建一套考虑障碍物的二维地形，建立全局最短路径的数学模型，通过给定的出发点和到达点，程序能自动规划出最短路径。

荔玉高速公路是《广西高速公路网规划》“四纵六横三支线”布局中“纵二”荔浦至铁山港高速公路的组成部分，也是国家高速公路网G59广西境段重要组成部分。荔玉21分部1#取土场位于藤县境内，平均坡度达到50%。与弃土点间东西向长度约6km，南北向长度约5km。取土场内需要保护的树木较多，用地红线严格控制。因此，对该项目而言，场地内土石方调配和运输是制约施工进度的关键因素。

1.1 二维无向网络图建立

对于目标求解的最优路径问题，需要对原始的地形图信息进行抽象化建模，首先提取1#取土场地形图中的障碍物信息、通道信息等建立多边形图，图中黑色部分为障碍物区域，车辆不能通行。白色区域为车辆可通行区域，如图1所示。

图1 1#取土场地形提取图

根据Maklink图论理论，通过构造若干条自由链接线线可以将二维空间分割成若干不相交的区域，但要求二维空间中创建的图形都是凸多边形[1]。图1中创建的多边形并不完全是凸多边形，不满足Maklink图创建的条件，因此需要将该多边形进行凸化。一般而言，凸化方式为在现有的黑色障碍物多边形基础上向外扩展s长度。将扩展后的障碍物定义为含有缓冲区的障碍，即在实际汽车运输过程中，即使车辆沿着黑色障碍物区域边界行使也不会与实际障碍物发生碰撞。

一般而言，构造的Maklink自由链接线时应满足如下要求：（1）任意的2个凸多边形的连线不得与障碍物有交点；（2）每一个凸多边形顶点至少需要引出一条链接线与一个多边形顶点相交；（3）链线之间不得交叉；（4）凸多边形顶点可以与空间边界相交。在凸化后的模型上，作顶点到边界的垂线及相邻2个凸多边形障碍物顶点之间的连线，构建Maklink图。

构建完Maklink图后选取所有自由链接线的中点、平面边界点、起点和终点，互相两两连接，就构成无向网络图。1#取土场无向网络图如图2所示。

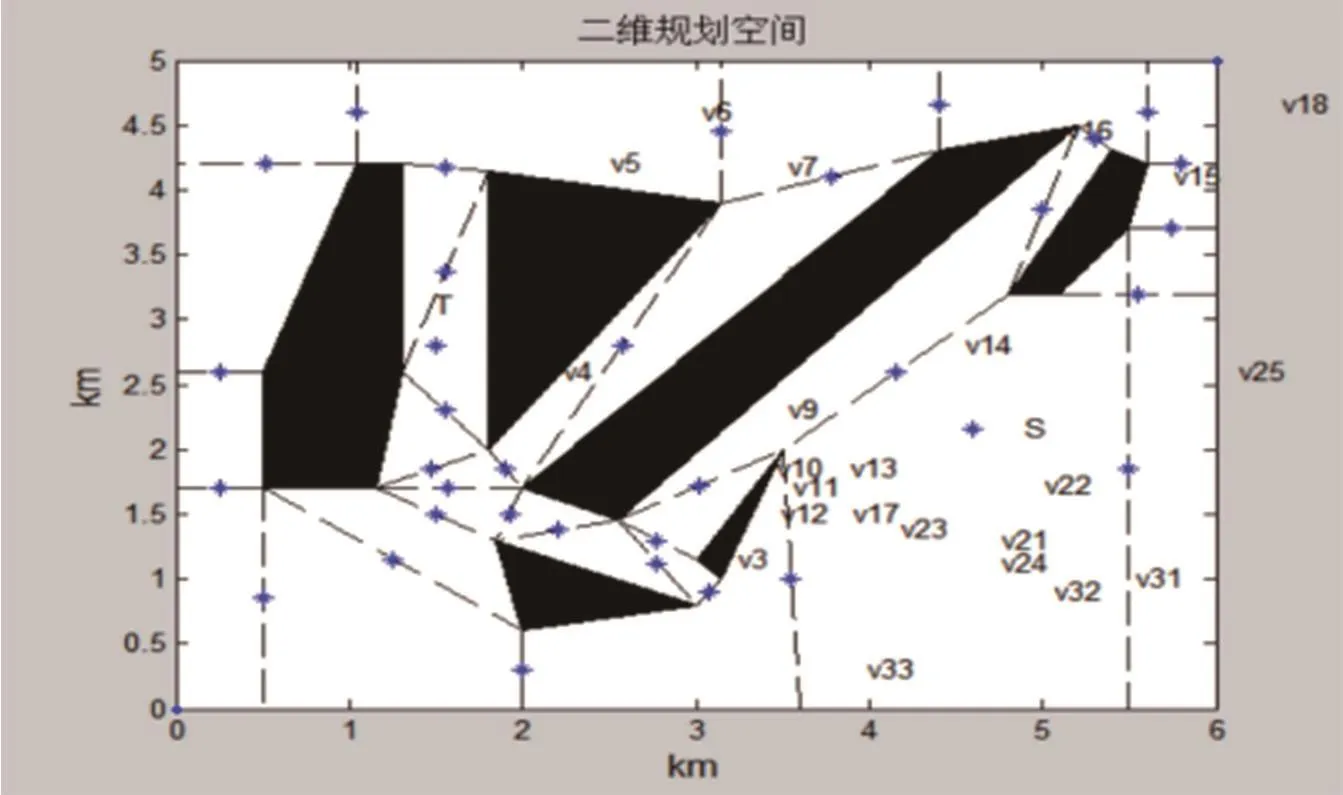
图2 1#取土场无向网络图

1.2 基于Dijkstra算法的初始路径规划

建立包含土石方运输出发点和到达点的1#取土场无向网络图后，为了避免后期蚁群算法进行二次优化时计算量过大，需先对无向网络图进行初始路径规划，以确定车辆行驶的大致方向。Dijkstra算法是典型的两点间最短路径算法，用于计算非负权值图中一个节点到其他所有节点的最短路径。引入2个距离集合（S、U），其中S集合包含已求出的最短路径的点，U集合包含未求出最短路径的点。初始化2个集合，从U集合中找出路径最短的点，加入S集合中并更新U集合路径。循环执行上述步骤，直至遍历所有节点，得到节点之间的最短路径。

在凸化后的无向网络图采用Dijkstra算法得到初始路径经过的链路为：S→V14→V9→V11→V13→V3→V8→V12→V5→T，初始化后的路径规划结果如图3所示（图中黄色线段为采用Dijkstra算法初始规划的二维空间次优路线）。

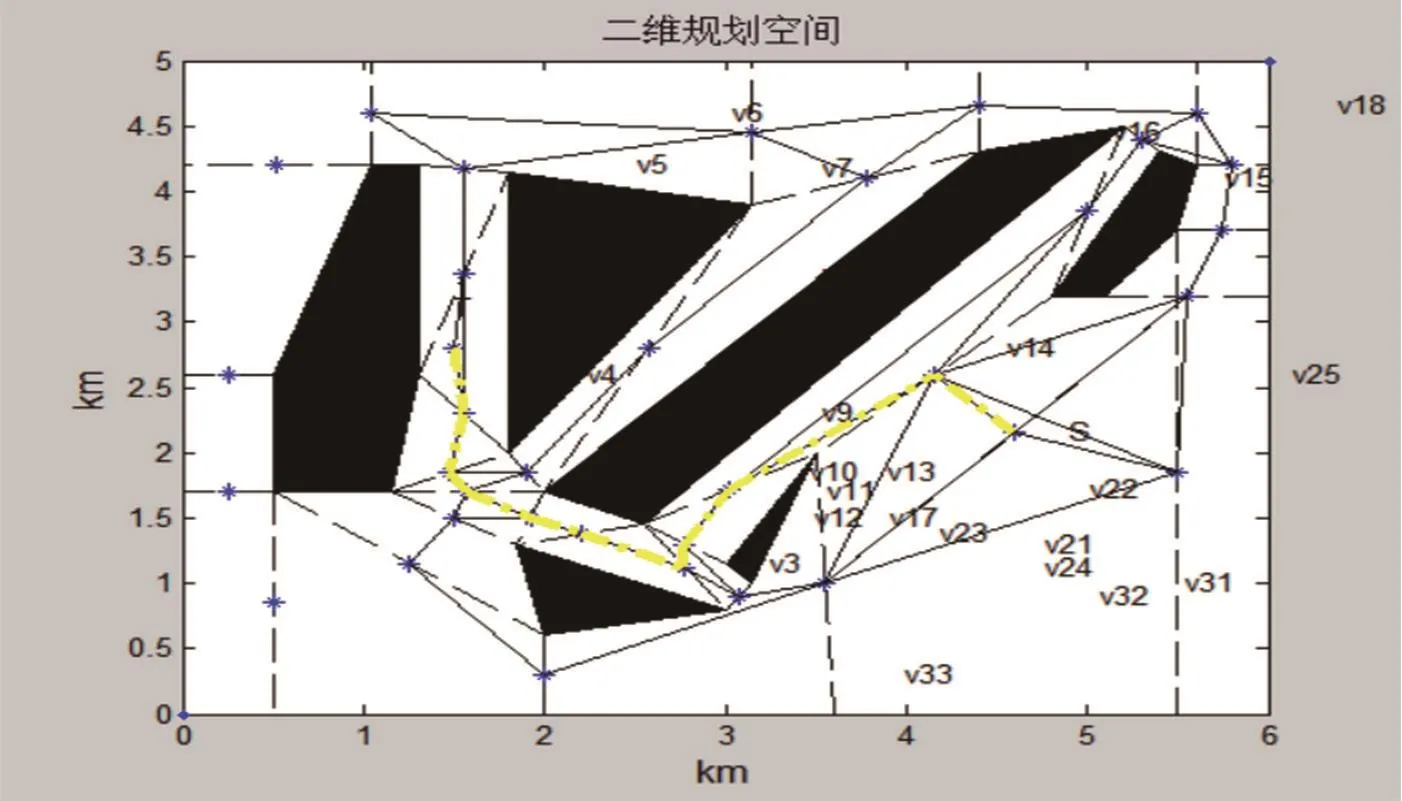
图3 Dijkstra初始规划路径结果

2. 蚁群算法路径优化研究

2.1 蚁群算法路径优化流程

蚁群算法是由Dorigo.M等人在20世纪90年代初通过模拟蚂蚁在搜寻食物时的行为开发出的一套算法，用蚂蚁行走的路径表示代求问题的可行解。行走路径较短的蚂蚁由于能首先获得食物，因此在沿途中释放的信息素较多。后方的蚂蚁总是趋向于沿着信息素较多的路径前进，随着迭代次数的增加，较短路径上聚积的信息素浓度逐渐增加。选择该路径的蚂蚁个数也增加[2]。最终，整个蚂蚁群体都会在正反馈的激励下聚集到最短路径上，此时对应待求解问题的最优解。蚁群算法最优路径搜寻逻辑如图4所示。

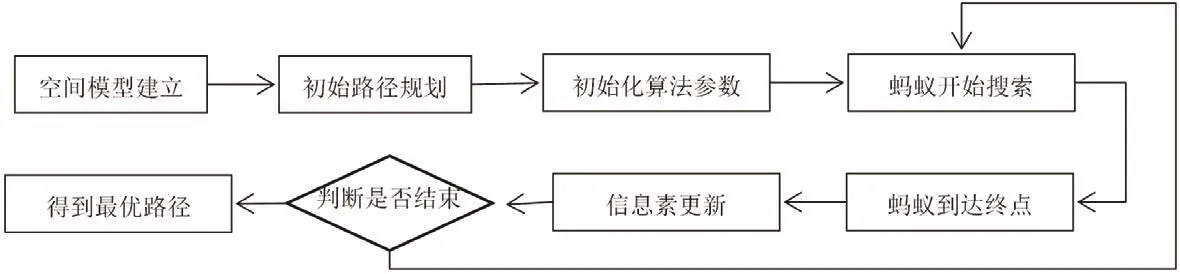
图4 蚁群算法流程图

蚁群算法优化寻找路径参数集合（h1，h2，...，hd），使得在离散化的空间里得到最短的路径。假设共有m只蚂蚁从起点出发到达终点，当蚂蚁在链线Li上搜索下一个节点Li+1时，方法为：

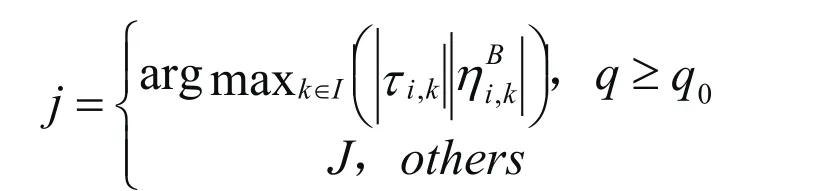
选择所有蚂蚁经过路径中长度最短的一段，更新该条路径上每一个点的信息素，即。其中，为最短路径的长度，ρ为[0，1]区间的可调参数。

2.2 工程算例与优化分析

以1#弃土场为例，模拟单次车辆运输最短路径。其中出发点位于G2地块S点，目的地位于D3地块T点。由前文Maklink图和Dijkstra算法得到的二维初始规划路径图引入蚁群算法，对每一个Dijkstra节点进行二次优化，其中选择的蚂蚁种群数量20，信息素选择概率为0.8，循环次数500次。得到的图像如图5所示。

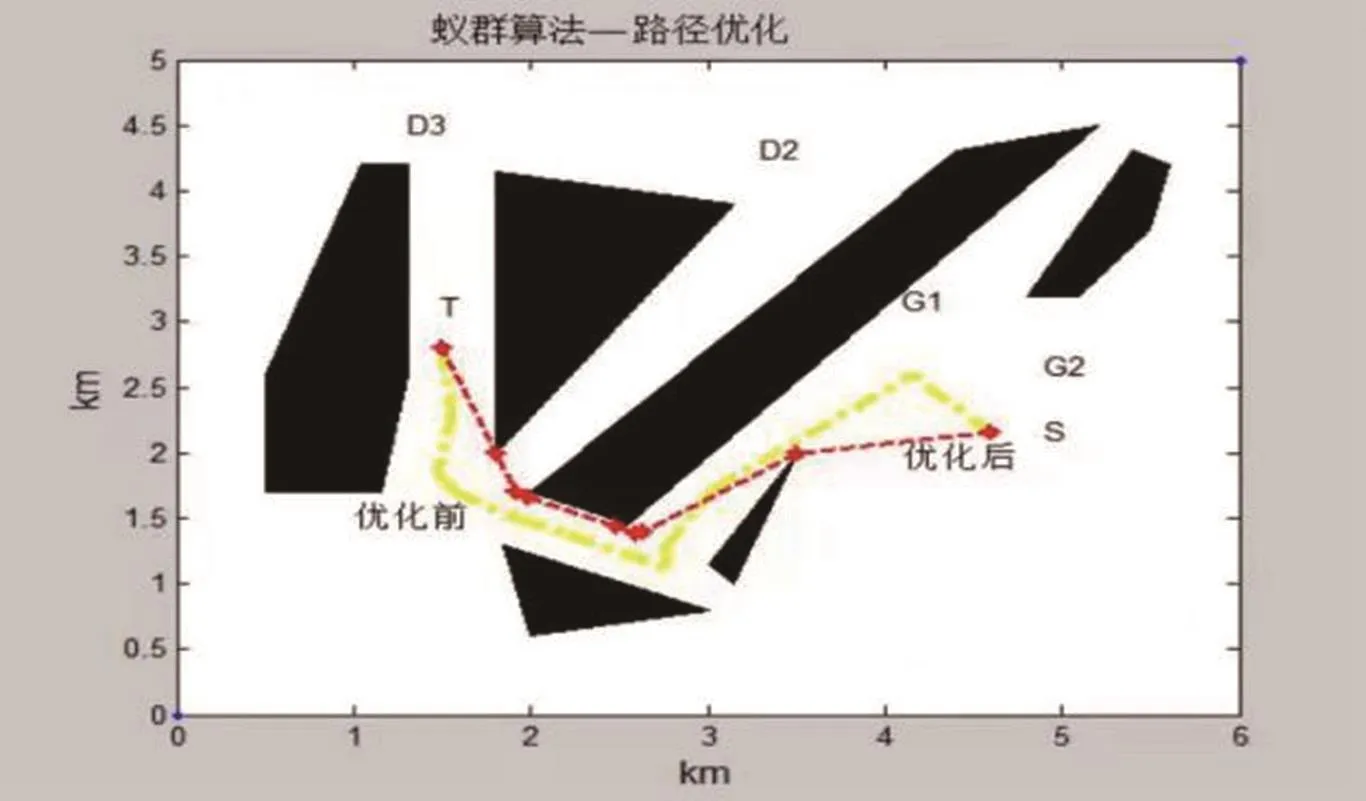
图5 路径优化结果图

图中省略了障碍物之间的Maklink线，并标注了各地块的相对位置。图中黄线部分为蚁群算法优化前的次优运输路径（即只通过Dijkstra算法在二维空间中规划的路径）。图中红线部分为经过蚁群算法优化后的最短运输路线图。通过在MATLAB中的计算，得出的从出发点S到终点T的最短距离为4.077km。从图中看出，最短的路径为从G2地块的S点出发，直线切过G1G2地块交汇处，连接G1地块拐点后贴着北侧向下经过D2地块，从D2地块沿直线到达终点T。

从算法性能上说，迭代500次时计算消耗时间3.6363s。通过蚁群算法，在前50次迭代过程中搜寻的路径长度迅速收敛，在第240次迭代后，搜寻的路径长度趋于稳定，算法整体性能较高。蚁群算法迭代搜寻示意图如图6所示。

图6 蚁群算法迭代搜寻示意图

从经济性上说，原规划的次优汽车运输路径长度为5.14km，通过蚁群算法的二次优化，将汽车运输路径长度缩减至4.077km。路线长度减少20.7%，能取得较好的经济效益。当汽车运输路线复杂途径障碍物较多时，通过蚁群算法优化后的路线长度优势更为明显。可以为今后汽车运输路线优化提供理论依据。

3. 结论

本文从运输路线建模，土石方运输路线初始规划和土石方运输路线二次优化调整等3个阶段展开施工过程中汽车运输路线规划研究。首先利用地形信息进行建模，产生扩展的凸多边形无向网络图。其次利用Maklink图和Dijkstra算法获得初始规划路径。最后采用蚁群算法对路径进行进一步优化得到满足要求的汽车运输线路[3]。

由仿真结果可知，本文采用的蚁群算法可以快速实现路线规划，与传统的手动进行路线规划相比，本文采用的路线规划方法能从全局的角度出发得到最短的路线，取得较好的效果。但本文仅考虑车辆在二维平面内的运输路线，并未考虑场地高程给汽车运输带来的路程增加影响，这将在下一步继续进行研究。