基于卷积神经网络的企业会计财务核算数据误差校正方法研究

王 强，余熙文

(1.淮北职业技术学院 财经系，安徽 淮北 235000；2.合肥师范学院 艺术传媒学院，安徽 合肥 230601)

卷积神经网络技术是现阶段高新技术研究中的热门，具有较强的表征学习能力.卷积神经网络被应用到各个领域中，得到了快速发展[1-3],在企业财务管理中具有很重要的实际意义.企业发展中，离不开财务的管理与运作，对于企业财务的管理，离不开数据的核算.企业正常经营中，每天都会产生大量财务数据，需要会计人员统计和审核，一些细微误差会导致企业财务出现异常，严重情况下会造成企业财务危机，影响企业正常运营[4-6].面对这一问题，一些技术人员和相关专业专家提出了相应校正方法，通过适当技术手段校正数据误差，获得准确的数据核算结果.

文献[7]提出基于线性回归的校正方法，该方法能够准确检测出数据误差，具有一定数据还原能力，将数据校正为正确状态，但是在网络噪声工作环境中，容易受到网络波动的影响，造成数据丢失等情况，数据的可靠性较差.文献[8]提到基于粒子群优化的校正方法，该方法利用优化后的粒子群，实现数据的自动校正，具有较高的校正精度，但在网络噪声工作环境下，同样存在数据可靠性较差的问题.

为解决上述方法中存在的问题，本文将卷积神经网络技术应用到校正方法设计中，通过检测企业财务数据中存在的误差，并将获取的误差数据借助卷积神经网络进行有效分类，并预测核算数据下一状态变化，引入外控制量并求解，根据控制量的变化校正数据误差.

1 企业会计财务核算数据误差校正方法设计

1.1 财务核算数据误差检测

为实现企业会计财务核算数据误差校正，需要检测企业财务核算数据的误差量.因此，本文检测了企业财务核算数据的误差.

假设企业会计财务核算数据集设置为：

W=[w1,w2,…,wn]∈R+，

(1)

式中，w代表数据集合中组成因子，n表示数据集中核算数据的数量.

在会计财务核算数据检测集内误差U表示为：

U=[u1,u2,…,um]，

(2)

式中，u代表核算数据检测因子.

会计财务核算数据误差检测之前，分解W，得到：

W=HHT.

(3)

并将数据集转换为另一种形式，如下：

Wc=H-1W=H-1U+H-1E，

(4)

式中，H表示下三角矩阵，H∈R+，E表示期望值[9].

计算Wc的方差矩阵，定义期望值为：

(5)

对Wc进行奇异值分解，分成前m-v个奇异值与后v个奇异值，其表现形式为：

(6)

式中，Z表示Wc列组成的正交输入基向量，D表示正交输出基向量，v表示约束矩阵行数.

通过上述计算获得最小特征值近似为1的个数即为v的取值[10].求解上述公式，即可得到数据集的误差结果为：

U=HXc.

(7)

在获得数据误差后，利用卷积神经网络确定数据之间、误差之间及数据与误差之间的关系，以数据间关系作为依据，校正数据误差.

1.2 财务核算数据间关系确定

根据上述检测的财务核算数据中存在的误差，利用卷积神经网络搭建数据分类模型，将财务核算数据作为模型的输入量，通过分析数据的特征向量，判断财务核算数据间变量的关系[11].构建的财务核算数据分类模型框架如图1所示.

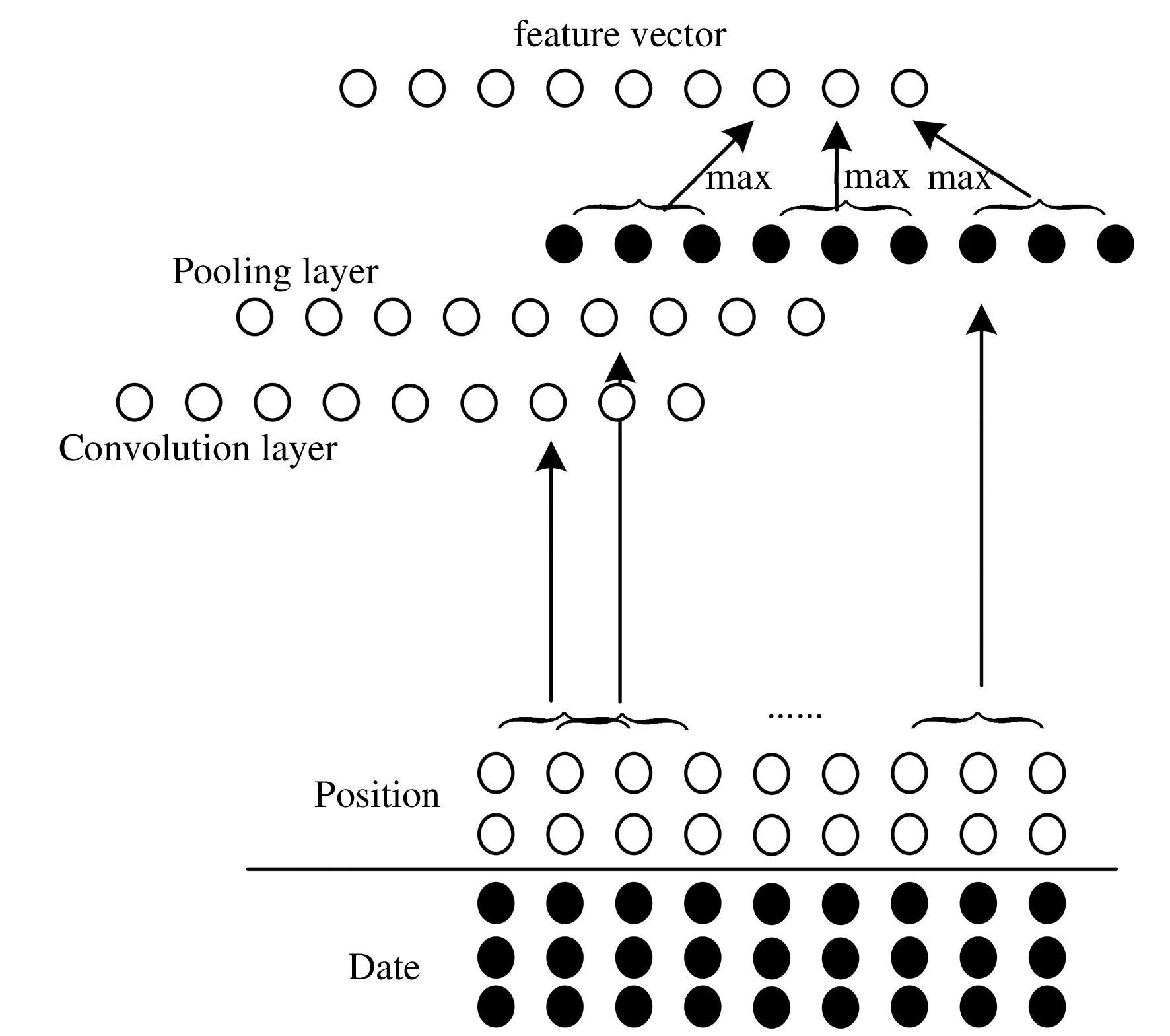
图1 财务核算数据分类模型框架

在模型内主要负责处理财务核算数据的内容为池化层和卷积层，考虑到数据关系的特殊性，对卷积层与池化层之间的连接方式重新设计，具体设计内容如图2所示.

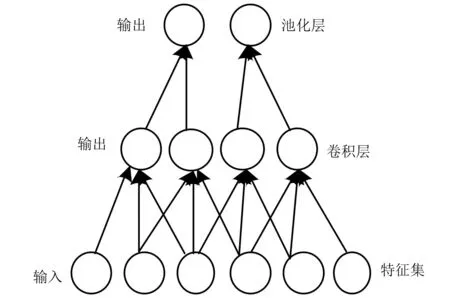
图2 卷积层与池化层连接设计

假设输入到模型内的财务核算数据为A={a1,a2,…,a|a|}，其中，ai表示数据的第i个序列，使用Ai:j表示串联序列矩阵[ai:ai+1:…:aj]，与数据进行卷积操作，得到另一个向量p表示为：

pj=K⊗A(j-k+1):j，

(8)

式中，1≤j≤|A|-k+1，K表示卷积层的权值矩阵[12].

使用滤波器捕捉输入数据的不同特征，财务核算数据的卷积运算表示为：

pij=Ki⊗A(j-k+1):j，

(9)

其中，1≤i≤n，通过模型中卷积层，即可得到矩阵P={p1,p2,…,pn}.将矩阵P分成3部分，pi={pi,1,pi,2,pi,3}，通过池化层处理得到被分段的向量：

ηij=max(pi,j).

(10)

将向量ηij组合到一起，得到一个数据完整的特征向量为：

tA=tanh(η).

(11)

通过点乘计算，得到数据A对应的类别标签，得到该类别标签的类别向量，组合成类别矩阵TA.

依据各数据类别，即可确定数据间关系.在已知数据误差和数据间关系的情况下，实现对数据误差的校正.

1.3 企业财务数据误差校正实现

根据上述分析，已知财务核算数据的误差是随机误差和核算误差之和，表示为：

Δyb=Δsyb+Δoyb.

(12)

为了精准校正数据误差，向前一步预测数据得到的误差表示为：

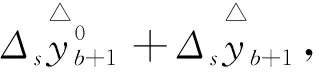
(13)

式中，s和o分别表示随机误差和核算误差的特征，b表示当前数据状态.

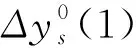
(14)

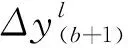
(15)

求解上述公式，计算外控制量x，即可求得b状态下修正预测值，完成对核算数据误差的修正.

2 实验分析

2.1 实验准备

选取某公司财务数据用于实验研究，该数据符合客观性、可比性以及可获得性，考虑到该样本企业财务状态，将研究目标设定为被特别处理的上市企业，采集该上市企业上一年年报数据信息，将这些数据用于企业会计财务核算数据误差校正实验研究中.采集的企业财务数据中可能包含一些歧异，这是由于财务报表自身问题造成，在实验中可能会对实验结果产生影响.因此，在获得数据后，处理样本数据，消除数据之间的歧义.由于财务指标数据意义不同，对数据归一化处理，公式如下：

(16)

式中，i表示实验数据集中的数据编号，i=1,2,…,N，N表示全部数据数量，Gi表示第i个数据样本的归一化值，xmax表示数据样本的最大值，xmin表示数据样本的最小值.在归一化处理后，使样本数据分布在[-1,1]之间.

实验中，引入基于线性回归的数据误差校正方法和基于粒子群优化的数据误差校正方法，实验设计是为了验证各校正方法的实际水平，但在实验过程中，实验结果会受到各项参数设定的影响，因此，结合实际企业财务状态，在实验中选择适当的模型参数，设置数据的窗口大小为3，向量维度为5.实验数据规模、分布特征与数据误差校正效果存在关系，数据规模越大，校正过程中需要的计算量越多，数据规模太小，又会导致校正效果不好.为了消除这一影响因素，使用matlab中的核密度估计函数，处理实验数据，计算数据集的区域概率值.分别取数据规模为10、100、1 000，获得核密度估计结果如图3所示.

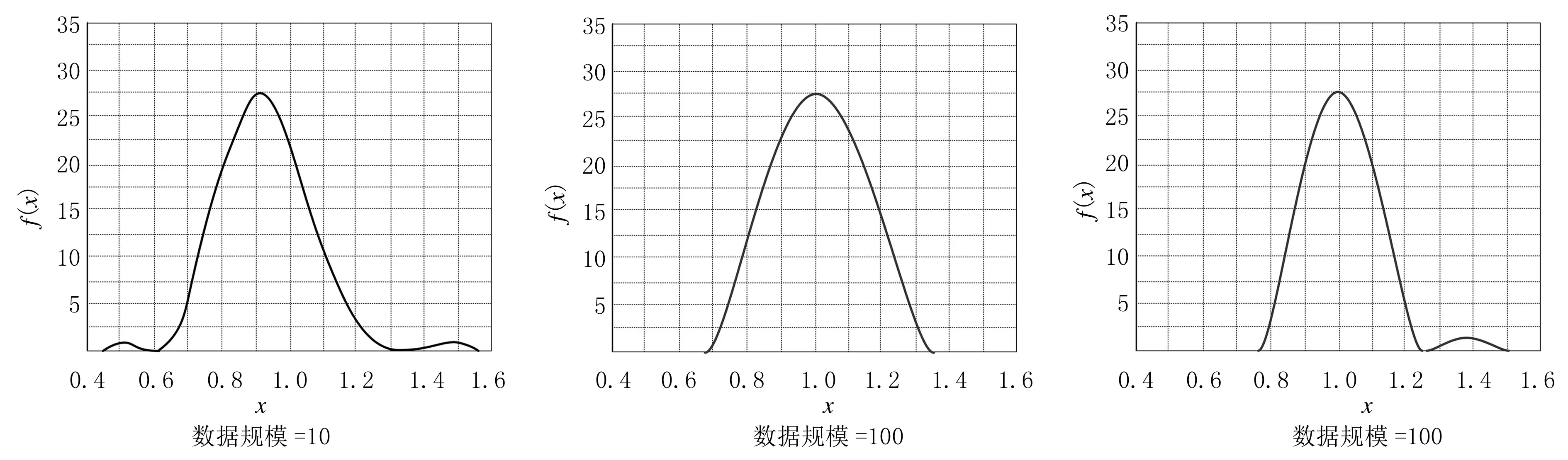
图3 数据集的区域概率值估计

从图3中显示的3组估计结果可知，当数据规模为10时，历史数据过少，估计值出现了比较严重的偏离，分布效果并不理想，当数据规模为1000时，分布情况与理想分布较接近，但是存在较多的运算量，相比之下，当数据规模为100时更适合实验研究，此时数据规模的状态与理想状态基本相符，并且运算量较少.因此，在不影响数据误差校正效果的前提下，实验中选取100作为实验数据规模.

2.2 实验结果分析

在会计财务核算数据误差校正过程中，数据补偿是一个非常重要的环节，补偿效果对数据的质量影响比较大，补偿效果越好，校正后的数据质量就越高.因此，为了验证不同校正方法中数据补偿效果，设计对比实验，以数据的累积分布图作为实验结果，设定不同的误差等级，分析不同误差等级下，数据得到补偿的百分比.实验设置两种情况，一种是在正常工作环境下，另一种在网络噪声干扰的工作环境下，实验结果图4所示.

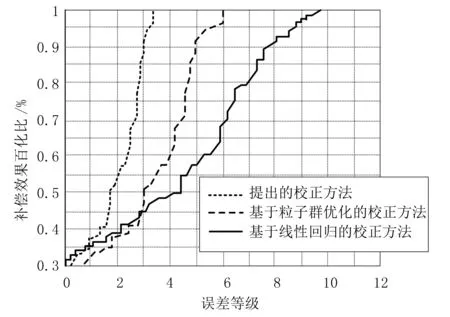
(a)正常工作环境下不同校正方法补偿效果实验结果

(b)网络噪声环境下不同校正方法补偿效果实验结果图4 不同工作环境下校正方法补偿效果实验结果

从图4中可以看出，图a在正常工作环境中，3种校正方法在实验过程中均能达到100%的补偿效果，但对比分析可知，提出本文校正方法能够在面对较高误差等级时，更快速地实现数据补偿，而其他两种校正方法面对高等级的误差需要缓冲.观察图b实验结果，在网络噪声环境下，基于线性回归的校正方法没有在实验内达到最好的补偿效果；基于粒子群优化的校正方法虽然在实验内达到最佳补偿效果，但是与正常工作环境下的补偿效果相比，并不理想；提出的校正方法在网络噪声环境下依然能够保证高水平的补偿效果，说明该方法使财务核算数据质量能够得到保障.

在企业财务核算数据完整性实验中，以数据的辍出率和数据方差作为指标.数据辍出率为数据在误差校正过程中损失的数据，其值越大说明数据损失越大；数据方差表示数据的离散性，数据离散程度越大，计算的数据方差越大，在处理过程中越容易丢失数据.数据辍出率的计算公式为：

(17)

式中，y表示真实数据的权重，a表示辍出数据.

经过计算与统计，得到不同校正方法的数据完整实验结果，如表1所列.

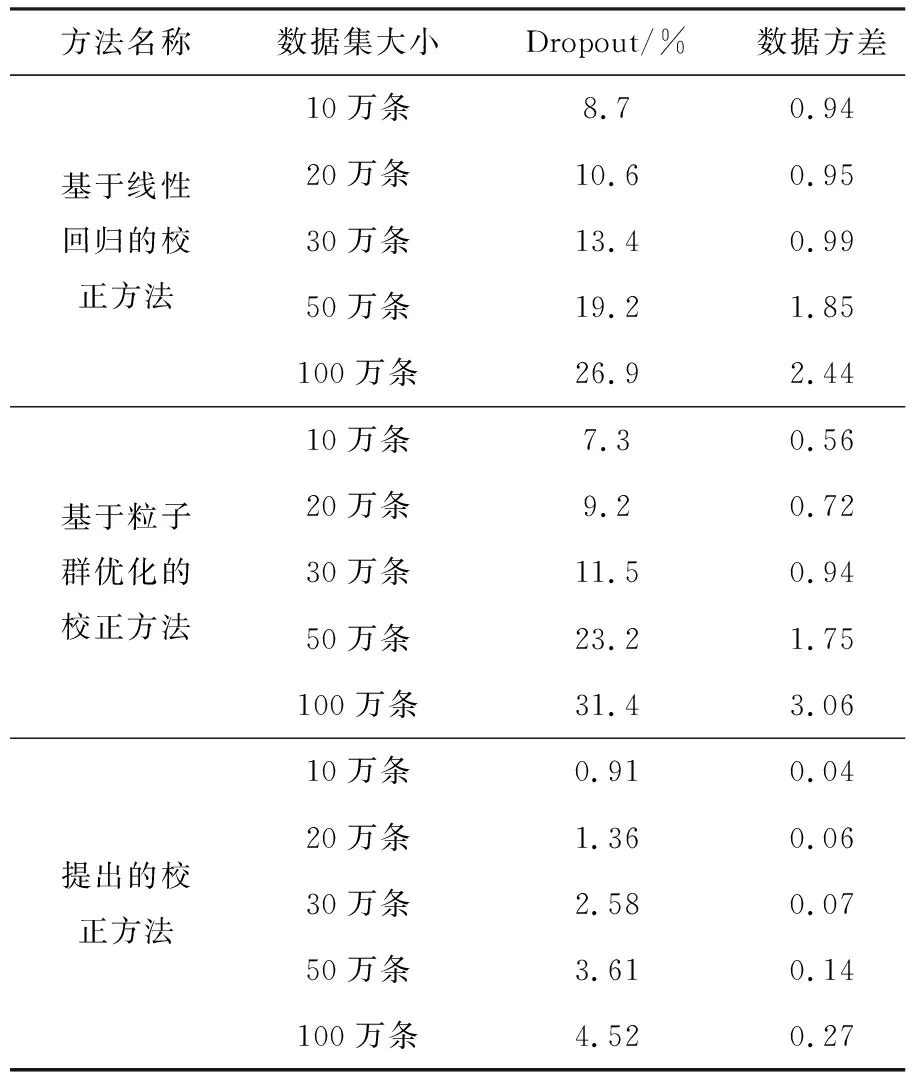
表1 不同校正方法数据完整性实验结果

实验中数据辍出率大，数据方差大，说明数据完整性差，数据丢失情况严重；反之，数据辍出率小、数据方差小，说明数据完整性好，财务核算数据安全完整.观察表1中数据分布情况可知，实验中引入的两种校正方法辍出率较高，数据方差也比较高，随着数据集大小的变化，辍出率和数据方差随之升高，最高达到了31.4%和26.9%；提出的校正方法虽然也存在数据方差和辍出率升高的情况，但是数值变化较小，最高为4.52%，在可控范围内，对数据误差校正效果小，该校正方法得到的数据完整性更好.

3 结语

本文以企业会计财务核算数据误差校正作为研究目标，将卷积神经网络引入到校正方法中，重新设计校正方法，并在方法设计完成后，通过对比实验对校正方法的应用水平进行了验证，解决了传统校正方法中存在的一些问题.由于受到技术手段和研究环境的限制，研究过程中忽略了一些研究细节，导致该方法存在一些不足之处，将在后续研究中逐一完善.