巧用错题本,提高初中生数学解题能力
廖晓兴



[摘要]分析学生“连续犯错”的根本原因,探讨纠正“一错再错”的方法,引导学生正确认识错误,开展有效指导。归纳解题策略,提高解题能力。精准收集分析,提高纠错实效。关注“一错再错”的纠正效果,巧用错题本,提高初中生数学解题能力。
[关键词]根本原因;认识错误;归纳策略;收集分析;建立错题本
初中数学教学中,普遍存在低效、无效化现象,教学过程中,不难发现许多学生在练习、作业或者考试时,出错的题在下一次还会继续犯错的现状。为此,我作为成员加入深圳市罗湖区《利用“错题本”提高数学教学效率的研究》小课题进行深入研究,研究发现:巧用“错题本”,可有效纠正“一错再错”的现象,提高初中生数学解题能力。
一、“连续犯错”的根本原因
学生出现“连续犯错”现象的根本原因:一是学生在学习新知时,没覆盖重点、难点和易错点,致使训练存在缺失、遗漏,导致踩坑、丢分;二是学生没有养成订正错误、标记错题和分类收集错题的习惯;三是纠错方法与途径缺乏专业的指导;四是学生对知识点间的联结能力弱,不能举一反三。
二、糾正“一错再错”的方法
(一)正确认识错误,开展有效指导
大部分成绩停滞不前的学生,学习和做题时都是停留在舒适区,满足于已掌握的题目,这一类题目属于无效成功。但是,学生的有效错误比无效成功更重要。在教学过程中,正确认识有效的错误,指导学生将以下两类有效错误收录到错题本中:第一类是考前已掌握,但考试时状态不佳犯错的题目;第二类是考试时盲目猜测,但经过评讲后,学生能掌握的题目。让学生订正错误时,多停留一段时间,让大脑充分思维,理解题目考察的知识点和解题技巧。此外,为切实减负,对一些简单易懂的错题,不必要求重复训练。而一些难度较大的题目,学生不易理解和纠错的,将其记录在错题本中,必要时,应指导学生进行多角度的训练,使学生得到有效的纠错。
例如,基本式:如右图,点A、B、D、E在同一直线上,AD=BE,BC//DF,∠C=∠F,试说明AC=EF。
由于AD和BE不是△ABC和△EDF的对应边,证明△ABC≌△EDF时,学生容易出错。
应引导学生先减去公共边,AD-BD=BE-BD,即AB=DE。再使用AB=DE和其他条件(根据平行线的性质得出∠DBC=∠BDF,由等角的补角相等得出∠ABC=∠EDF,由全等三角形的判定定理)证明△ABC≌△EDF,最终得出对应边AC=EF。
为达到纠错效果,可通过下面的变式1、2进行多角度的训练,由联结公共边证明三角形全等,并类比延伸到联结公共角证明三角形全等。
变式1:已知点A、F、E、C在同一条直线上,AF=CE,BE//DF,BE=DF,求证:△ABE≌△CDF。
变式2:已知AB=AC,AD=AE,∠1=∠2,求证△ABD≌△ACE。
(二)归纳解题策略,提高解题能力
初中数学课程中,主要包括如下四大模块。一是数与代数:实数、整式和分式(包括因式分解等)、方程和方程组、不等式与不等式组、函数等。二是空间与图形:图形的认识、图形与变换、图形与坐标、图形与证明等(包括全等、相似、三角形、四边形、圆等)。三是概率统计。四是实践与综合应用。在教学过程中,教师要引导学生对学习的各个新知识进行全面的归纳和梳理,让学生掌握各个知识点、重点和关键点及知识体系等,并引导学生总结出相应的解题策略。如:一些特殊几何问题,可通过画辅助线、割补法及等量代换等。解决与图像的选择题,可运用数形结合法。求函数关系式时,运用待定系数法。因式分解中,运用拆项、添项法等……这样,有助于学生对容易出现的各类错误进行纠正。此外,要指导学生进行各类题型的累加练习和一些特殊问题的练习等,让学生见多识广,不断积累实践经验。实践证明,通过上述方法,能有效地提高学生的解题能力,并减少解题错误。
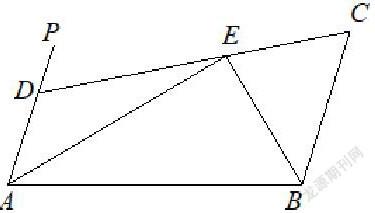
如右图,AP//BC,∠PAB的角平分线与∠CBA的角平分线相交于E,CE的延长线交AP于D,试说明AB=AD+BC。
AD和BC是不在同一直线上的两条线段,需要用三种方法等量代换:
1.全等三角形的两条线段相等;
2.垂直平分线上的点到线段两端的距离相等;
3.角平分线的点到角的两边距离相等。
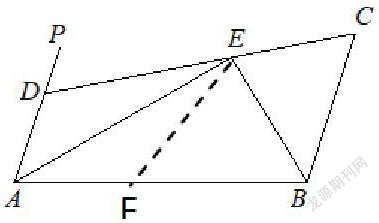
在AB上截取AF= AD,根据角平分线的性质证明△DAE≌△FAE。
结合等角的补角相等及平行线内错角相等的性质,分别可得出:∠PDE=∠EFB,∠PDE=∠ECB,从而,可证△BFE≌BCE,得BF=BC,因此,AB=AF+BF=AD+BC,利用全等三角形的两条线段相等,等量代换,证明等式。
(三)精准收集分析,提高纠错实效
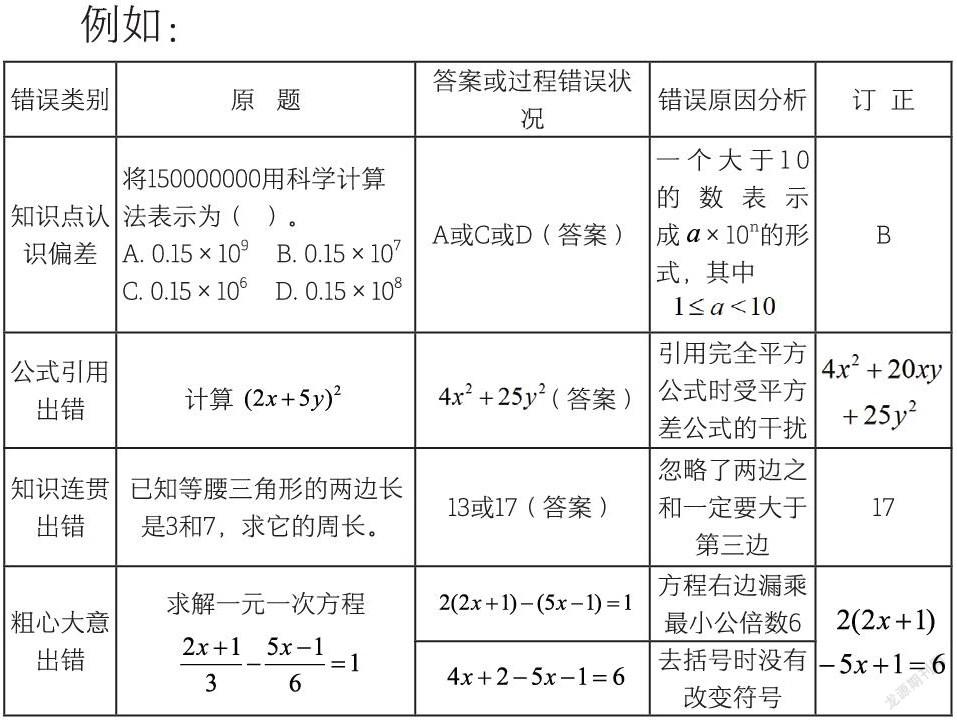
教学实践中发现,学生容易出现的错误形式:1.知识点认识偏差。2.公式引用出错。3.知识连贯出错。4.粗心大意出错(抄错数字、上下前后答案对调、漏算、计算失误等)。为了对分类收集错题进行专业指导,我的做法是:不仅要针对普遍出现的错误进行收集,及时汇总个人重复犯错的误区,还要对压轴题的解题思路进行梳理等。引导学生针对性地选择错题进行记录,分析出错的原因,并将其“抄”下来,明确其易错类别,分析错误的原因,订正错误,并建立错题本。学生的学习过程,就是不断充实和完善自我的过程,通过上述长期训练,能有效地培养学生审题能力和对错误的辨析能力、分类能力、文字表述能力等,同时,要注意引导学生学会“举一反三”,灵活运用,为纠正“一错再错”夯实基础,最后达到预防直至避免错误。
例如:
三、“一错再错”的纠正效果
基于德国心理学家艾宾浩斯研究发现的遗忘曲线,在研究过程中,对学生答题出错的现象和再次出错的原因进行复盘和分析,不难发现,没有整理纠错习惯的学生,仍然时有再现“一错再错”的现象。有建立错题本习惯的学生,能及时得到总结和梳理,“一错再错”的现象明显减少。实践证明,巧用“错题本”能取得良好的纠错收效,能提高初中生数学解题能力。
数学家华罗庚曾说:新的数学方法和概念,常常比解决数学问题本身更重要。在教学过程中,教师要对学生进行专业指导,归纳解题策略,引导学生分类收集有效错误,建立错题本,通过巧用错题本,能有效提高初中生数学解题能力。

