数学分析手段在煤矿岩性识别处理中的应用

郎 君，刘亚武，葛 军

(吕梁学院 矿业工程系，山西 离石 033001)

0 引言

中国作为能源储量大国，煤炭、石油、天然气及其他主要能源的储备量位居全球前列，随着浅部能源的勘探开发以及环保环境的制约因素，我国重要矿产的勘探新增资源量存在衰减趋势，从中国自然资源部公布的2020年中国矿产资源报告中可以看出，截至2019年底，我国煤炭的新增矿产资源量较2018年减少了256亿吨，天然气、煤层气及其他主要金属矿产也均有不同程度的缩减，但对这些矿产资源的勘查投资却逐年有所增加，其中，采矿业同比增长24.1%[1].我国的能源勘探工作由浅部地层逐步向深部地层迈进[2,3]，但深部地层附带的一些常规问题也愈来愈明显，例如深部地层地应力复杂、地质构造情况多变、岩性复杂难以识别等，这些问题都给我们的勘探开发工作带来很大的阻力，尤其是在含煤地层进行矿井设计工作时，若无法准确的提取地层岩性信息，将无法指导后续开采设计工作，且安全保障也将受到巨大影响[4]，所以，准确获取巷道地层信息和基础地质参数是我们煤矿工作的重中之重，务必高度重视.

1 方法原理

本次研究主要基于主分量分析技术，又称为主成分分析技术，旨在利用降维的思想，压缩数据空间，把涉及的多个参数指标，通过线性变换，将原有变量变换为新的线性组合，将这些数据变换到新的坐标系统中，其中数据投影的第一大方差标记为第一主成分，第二大方差标记为第二主成分，依次类推[5，6].通过这样的处理方式，使得数据集的维数减少，同时保留了包含重要数据成分的低阶主成分.处理过程如下[7]：

假设采集样本数为m，每个样本附带n个变量参数，形成m*n的一个样本矩阵，即，

Ai=[A1,A2,A3,…,An](i=1,2,3,…,m)

(1)

由于每个变量存在不同的数量级及量纲，为了避免这方面的影响，对采集样本进行标准化处理，

(2)

式中，aij为第i个数据的第j个指标，i=1,2,3,…,m，m为样本个数，j=1,2,3,…,n，n为每个样本的变量参数个数，μj和sj分别为样本均值和样本标准差.

求取各个参数相关系数rij，

(3)

进一步得到相关系数矩阵R(rij)m*n.

求取相关系数矩阵的特征值λj(j=1,2,3,…,n，n为每个样本的变量参数个数),及特征向量，最后计算特征值的累计方差贡献率，将贡献率大的选定为主成分进行分析识别.

2 实例分析

本次研究目的层选取山西某煤矿含煤层系地层，为海陆交互相含煤沉积地层，由灰黑色砂岩、页岩、碳质页岩夹煤层、石灰岩组成，是我国北方主要的含煤层系.

基于煤田测井曲线的响应特征[8](见表1)，选取目的层段响应特征较明显的几条测井曲线，作为本次研究样本，包括自然伽马曲线(GR)、声波时差曲线(AC)、补偿中子曲线(CNL)以及密度曲线(DEN)，由于自然电位SP是用于计算地层泥质含量的重要参数，深浅侧向电阻率的差值又可用于判别裂缝发育带的发育程度，所以将SP与深浅侧向电阻率的插值也作为岩性识别过程中的调整参数，一并列入主成分分析数据序列中.

表1 煤田测井曲线响应特征统计表

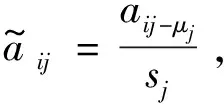
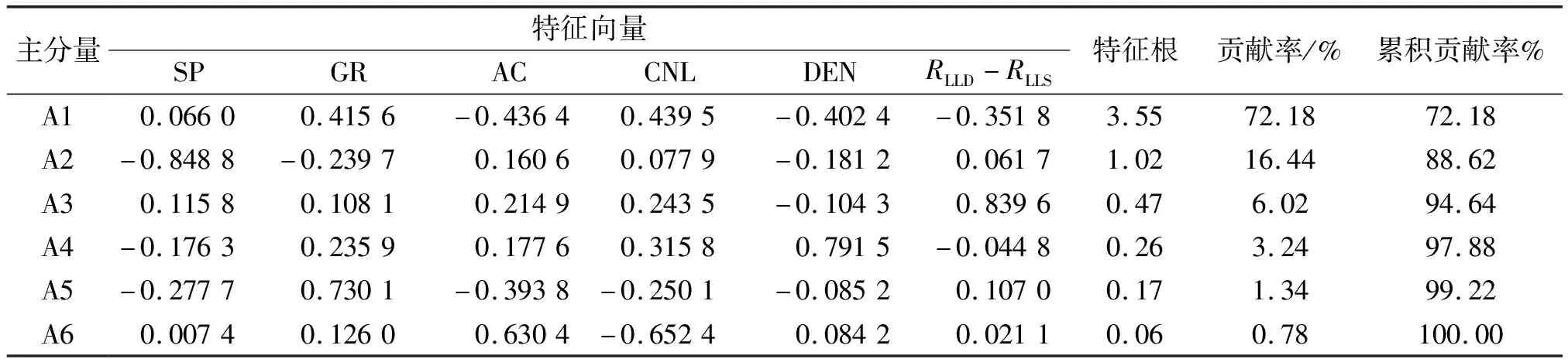
表2 特征值及贡献率计算结果

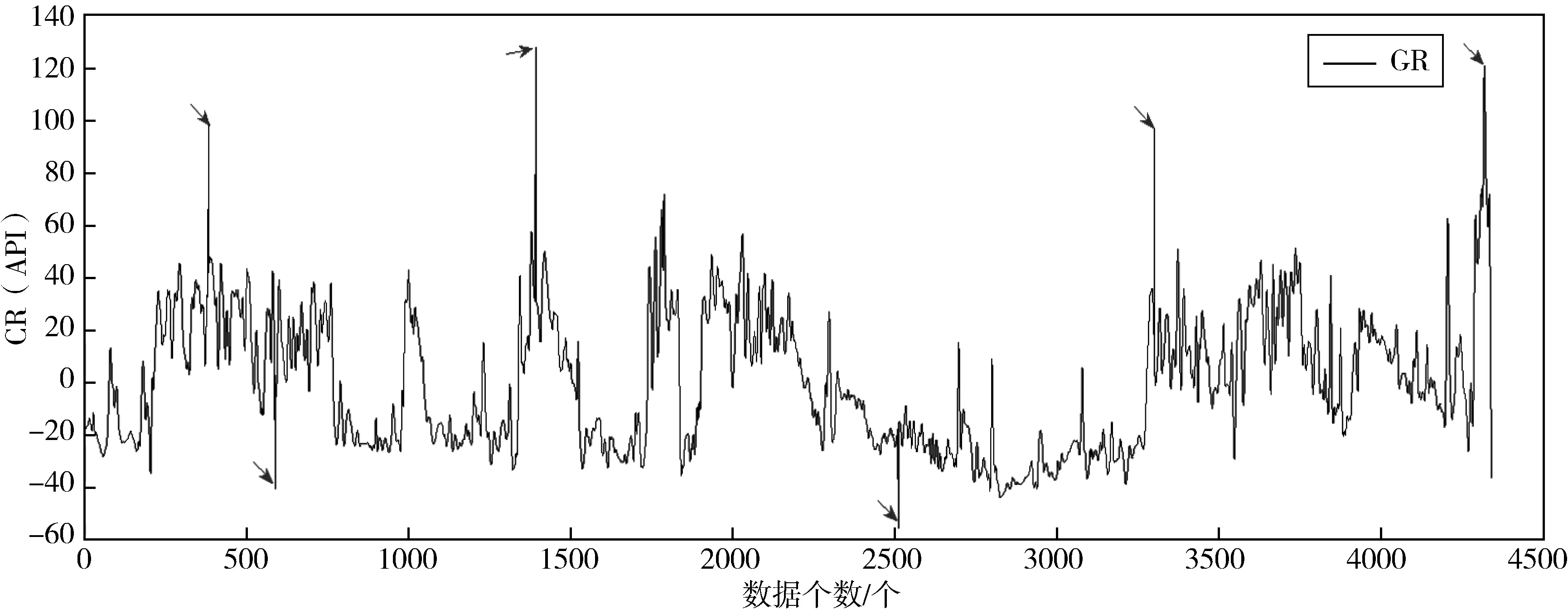
图1 数据序列中的异常点(数据来自煤田测井曲线GR值，MATLAB计算)

根据计算结果中各主分量的特征值所对应的特征向量，构建研究区含煤地层的主成分变换方程式：

A1=0.415 6GR’-0.436 4AC’+0.439 5CNL’-0.402 4DEN’+0.066 0SP’-0.351 8(RLLD-RLLS)’

(4)

A2=-0.239 7GR’+0.160 6AC’+0.077 9CNL’-0.181 2DEN’-0.848 8SP’+0.061 7(RLLD-RLLS)’

(5)

A3=0.108 1GR’+0.214 9AC’+0.243 5CNL’-0.104 3DEN’+0.115 8SP’+0.839 6(RLLD-RLLS)’

(6)

A4=0.235 9GR’+0.177 6AC’+0.315 8CNL’+0.791 5DEN’-0.176 3SP’-0.044 8(RLLD-RLLS)’

(7)

A5=0.730 1GR’-0.393 8AC’-0.250 1CNL’-0.085 2DEN’-0.277 7SP’+0.107 0(RLLD-RLLS)’

(8)

A6=0.126 0GR’+0.630 4AC’-0.652 4CNL’+0.084 2DEN’+0.007 4SP’+0.021 1(RLLD-RLLS)’

(9)

式中，GR’,AC’,CNL’,DEN’,SP’，(RLLD-RLLS)’分别为GR,AC,CNL,DEN,SP以及RLLD-RLLS经过样本数据标准化后的数值.

观察上述变换方程，可以看出A1-A6相互独立，A1的方差贡献率高达72.18%，A2次之，贡献率为16.44%，累积贡献率达到88.62%，由前人研究成果可知，若用累计方差贡献率来计算主成分个数时，一般情况下，当累计方差贡献率达到85%以上时，此时参与累计方差贡献率计算的主分量个数即为最佳的变量个数[9],说明应用A1和A2这两个主成分足以替代原有的6个变量，包含的信息能够体现样本特征.应用常规岩性交汇图分析方法得到研究区的GR-AC交汇图，如图2所示，图中所有岩样点均存在覆盖重叠现象，很难区分和识别具体岩性，尤其是当泥质含量较高的层段内，砂岩、泥岩及煤层更加难以判断，给岩性识别工作带来极大困扰.将计算得到的A1和A2两个主成分结果进行交会分析，得到的识别结果如图3所示.

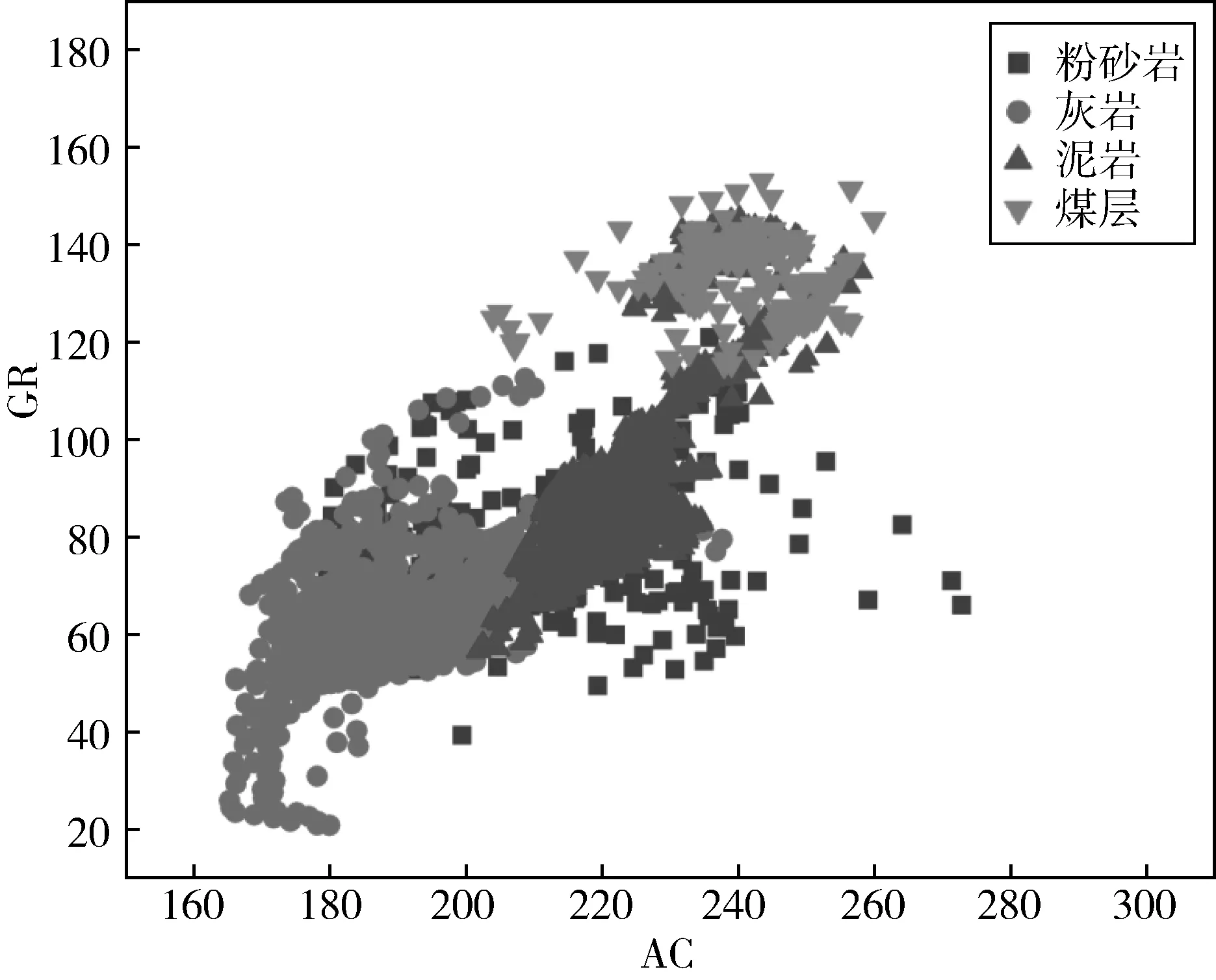
图2 GR与AC岩性识别交汇图

图3 主成分A1、A2岩性识别交汇图

由选定的两个主成分A1、A2绘制的交汇图能够很明显的区分主要岩性，除粉砂岩及灰岩类有部分交集外，泥岩和煤层能够有效的识别区分，岩性识别率得到了很大程度的提高.

4 结论

常规的岩性识别方法，由于各测井曲线之间存在相关性，且每个变量中的影响参数过于繁琐，使得维数增加，给岩性识别和判读带来困难，且识别准确率无法得到保障，以山西某矿地下实测煤田测井数据为例，采用主成分分析方法，通过累计方差贡献率敲定了足以替代所有变量参数的两个正交主成分，由主成分方程计算得到的交汇图结果，证实了该种方法手段的有效性，数据计算量更小，准确率更高，保证了煤矿下一步的采掘方案设计实施工作的顺利开展.该方法的关键在于通过降维的思想确定主成分的个数.