发动机传动箱流场的数值模拟研究

谭礼斌， 袁越锦，黄 灿， 唐 琳， 何 丹

(1.陕西科技大学 机电工程学院， 陕西 西安 710021； 2.隆鑫通用动力股份有限公司 技术中心， 重庆 400039)

发动机传动箱内的主动轮、从动轮及传动带之间是通过滑动配合实现变速目的的[1]。机械部件的运动可能会产生大量的摩擦热，造成机械部件温度的急剧升高。为确保传动箱内各机械部件能在合适的温度范围内高效可靠地工作，需要对传动箱进行良好的冷却。随着仿真技术的迅速发展，基于计算流体力学(Computational Fluid Dynamics,CFD)的数值模拟预测方法越来越多地应用于机械产品的预研开发阶段及产品性能提升阶段[2-6]。张付伟用CFD分析方法模拟了双离合自动变速箱内部各喷射油管喷口的质量流量和喷射轨迹[7]。刘宏伟等采用一维分析软件对CVT冷却系统进行了仿真分析，得出了过流面积和流动阻力对冷却系统流量有显著影响的结论，并用实验验证了数值预测结果的可靠性[8]。目前，CFD仿真技术已成为机械部件散热冷却分析研究及性能评估的重要手段[9-10]。

CFD 仿真技术实际上就是采用一系列流动控制方程，通过数值求解方法对流体流动问题进行的数值模拟。通过CFD仿真技术，可实现对复杂内部流场各位置各时间点的速度、压力、温度等物理量的直观展现。通过CFD分析，能对产品结构设计参数及设计方案的合理性进行评估与判断，以便有针对性地进行性能提升，达到产品最优化设计的目的。而以经验设计和实验验证结合的常规方法进行传动箱结构设计时，只有通过热平衡测试才能考察其冷却系统的设计效果，若冷却不理想，则需要多次结构改型和实验验证，因此会造成人力资源、实验资源的浪费与开发周期的延长。本文针对发动机传动箱冷却结构的两种设计方案，采用CFD方法，对传动箱内部冷却风速的流动特性进行数值模拟，对比分析传动箱冷却结构两种设计方案的风量及风速场，为传动箱的结构设计及评价提供理论参考。

1 发动机传动箱物理模型构建

首先采用3D建模软件CATIA构建发动机传动箱三维模型，然后将该模型导入流体分析软件STAR-CCM+中，进行几何清理、网格划分、边界设置和模拟求解，实现传动箱内部流场的数值模拟。图1所示为传动箱冷却结构的两种设计方案。其中，设计方案二是在设计方案一的基础上加大进风口面积，并调整了出风口位置。其主要目的是降低进风阻力和调整出风方向。降低进风阻力，有利于加大风量；而调整出风口位置后空气流动路径变长会造成风量降低。这两者综合下的风量提升水平是无法通过经验判定的。因此，需要采用仿真技术对两种设计方案的风量及风速场进行对比分析，以便快速确定传动箱冷却结构的设计方案。本文采用流体分析软件STAR-CCM+中多面体网格和边界层网格技术，实现传动箱计算流体域的网格划分。划分后的网格数量约为500万个。

(a) 设计方案一

(b) 设计方案二图1 两种设计方案的传动箱冷却结构Fig. 1 Two cooling structure designs of engine transmission case

2 数学模型选择及边界条件设置

假设空气在传动箱内部以不可压缩的湍流稳态流动，且空气流动遵守流体三大基本控制规则，即连续性方程、动量守恒方程和能量守恒方程[5,11]。本文的湍流计算选用k-ε两方程湍流模型。

根据文献[12]，连续性方程为：

(1)

式中：u，v，w分别为x方向、y方向和z方向的速度分量，m/s。

根据文献[13]，动量微分方程，即Navier-Stokes方程为：

(2)

式中：ρ为流体密度，kg/m3；Fx，Fy，Fz分别为x方向、y方向和z方向的体积力，N;μ为流体的动力黏性系数，Pa·s；p为流体微元体上的压力，Pa;2为拉普拉斯算子，例如

根据文献[14]，k-ε湍流方程为：

(3)

式中：t为时间,s;μt为湍动能黏度， Pa·s；k为湍动能,m2/s2；ε为湍流耗散率,m2/s3;xj为速度分量的方向，j=1,2,3；uj为对应xj方向的速度分量；Gk为速度梯度产生的湍动能项；Gb为浮力产生的湍动能项；YM为脉动扩张项；C1ε,G2ε,C3ε均为经验常数；Prk，Prε分别为对应湍动能k和湍流耗散率ε的湍流普朗特数；Sk和Sε为用户定义的源项。

传动箱内主动轮和从动轮旋转情况的仿真，可采用旋转参考系(MRF,Moving Reference Frame)方法来实现。在最小传动比时，主动轮的转速为 8 000 r/min，从动轮的转速为13 000 r/min;在最大传动比时，主动轮的转速为1 800 r/min，从动轮的转速为500 r/min。出口边界的设置如下：压力出口(Pressure Outlet)的压力为0。计算域的壁面参数采用Two-Layer All y+Wall Treatment 软件来设置。在流场模拟计算时，采用压力与速度耦合的SIMPLE(Semi-Implicit Method for Pressure Linked Equations)算法和压力基求解方法，并以二阶迎风格式对动量、湍流强度k和湍流耗散率ε进行离散化处理，使计算过程达到最佳的求解精度和收敛速度[15]。本文在CFD软件运行时，通过自动耦合方法求解连续性方程、N-S方程，并建立k-ε两方程湍流模型，获得相应的流场细节信息。

3 结果分析及讨论

3.1 风量

图2所示为传动箱冷却结构的两种设计方案在大、小传动比状态下的总风量对比。从图2可以看出，设计方案二在小传动比、大传动比状态下的总风量分别比设计方案一增大约20.9 g/s和10.7 g/s，风量分别增加约21%和65%。相对于设计方案一来说，设计方案二的风量明显增大，原因在于其进风口面积增大，降低了进风阻力，有利于提升总风量。

图2 两种设计方案在大、小传动比状态下的总风量对比Fig. 2 Comparative analysis of air quantity for two engine transmission designs at big and small transmission ratios

3.2 传动箱表面速度

图3、图4分别为小传动比状态下和大传动比状态下各截面风速的分布云图。各设计方案中截面包括：传动箱中截面、与出口平行的中截面、传动带中截面和传动箱中间横截面。

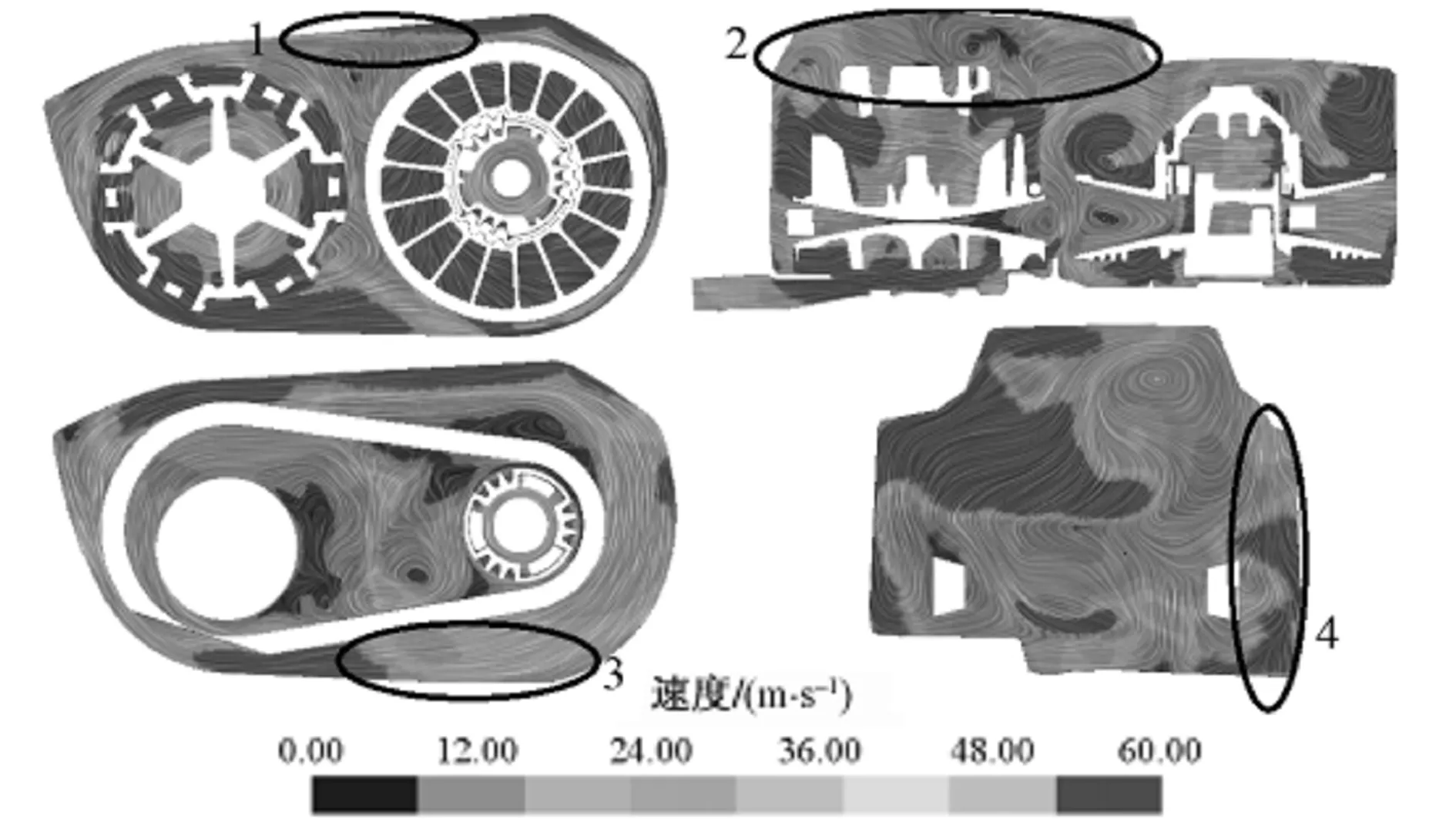
(a) 设计方案一

(b) 设计方案二图3 小传动比状态下各截面风速的分布云图Fig. 3 Velocity distribution comparisons of each section at small transmission ratio state

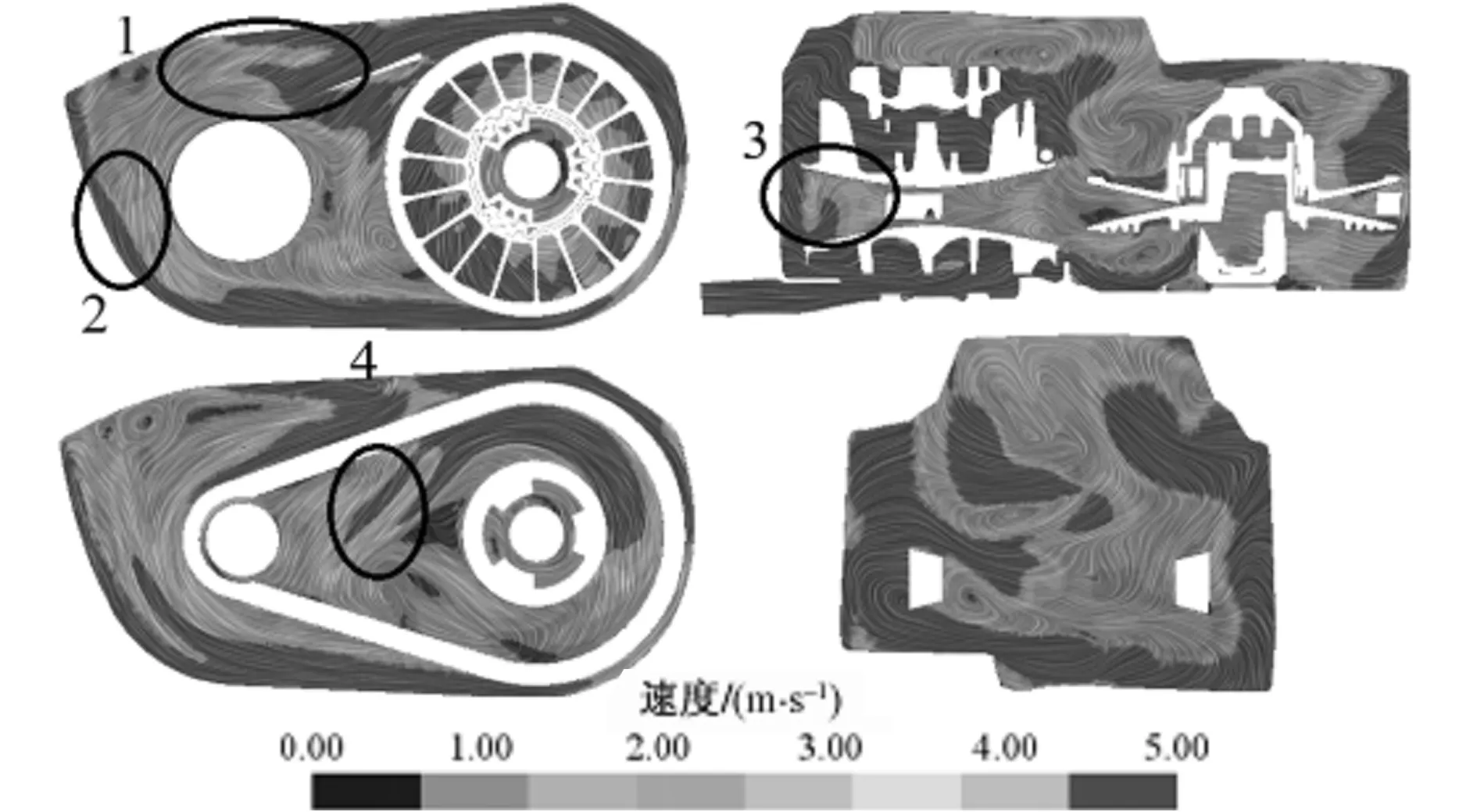
(a) 设计方案一

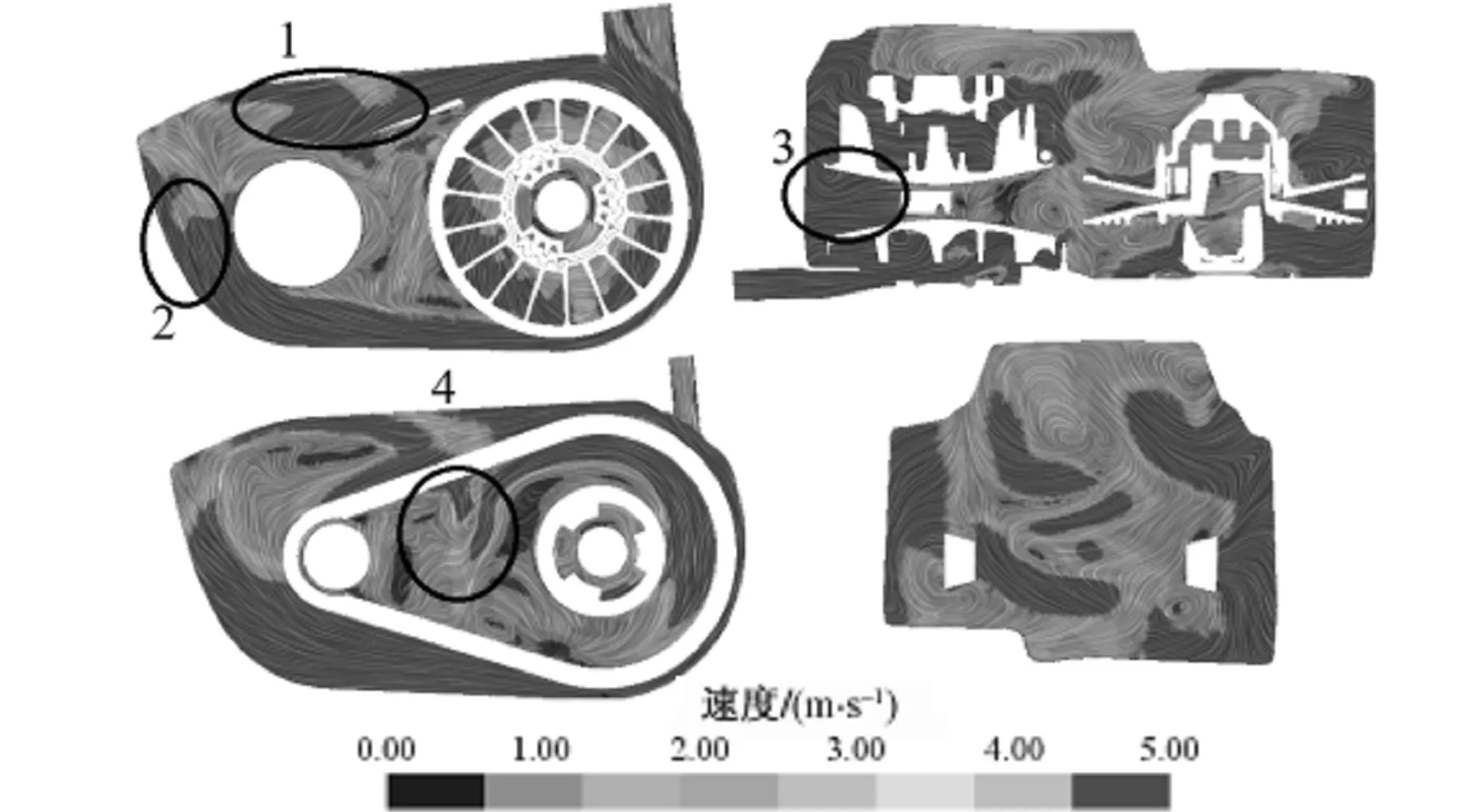
(b) 设计方案二图4 大传动比状态下各截面风速的分布云图Fig. 4 Velocity distribution comparisons of each section at big transmission ratio state

从图3、图4可以看出，设计方案二在图示圈出区域(区域1、区域2、区域3、区域4)的风速分布明显优于设计方案一。其具体表现在：小传动比状态下，区域1的风速分布较好，区域1中含速度标尺“60”的面积更大，表示风速大的区域面积增大，有利于该区域及其附近传动带的冷却；区域2同区域1，表面风速分布良好，风速较大的区域面积也略有增大，表示冷却性能有提升，也有利于该处传动部件的冷却；区域3和区域4也与传动带的冷却紧密相关，区域3和区域4的大风速区域面积增大更为明显，从原来大面积的风速在速度标尺“48”左右提升至大面积的风速在速度标尺“60”，风速提升非常明显，有利于该区域及其附近传动带的冷却。

传动箱大传动比状态时，与传动箱小传动比状态下具有类似的风速提升趋势，设计方案二的区域1、区域2、区域3、区域4表面风速的分布情况均比设计方案一好，对该区域及附近传动带冷却有利。由此可见，设计方案二的空气流动特性明显优于设计方案一。

3.3 传动箱内部件表面风速

图5、图6所示分别为小传动比状态下和大传动比状态下传动箱内部件表面风速的分布云图。图中灰度最大的区域为风速最低的区域；左边为主动轮，右边为从动轮，主动轮和从动轮的转动通过传动带实现。

(a) 设计方案一

(b) 设计方案二图5 小传动比状态下传动箱内部件表面风速的分布云图Fig. 5 Surface velocity distribution of internal parts of transmission case at small transmission ratio state

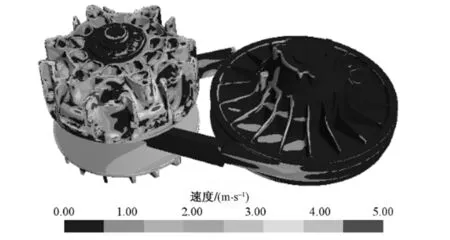
(a) 设计方案一

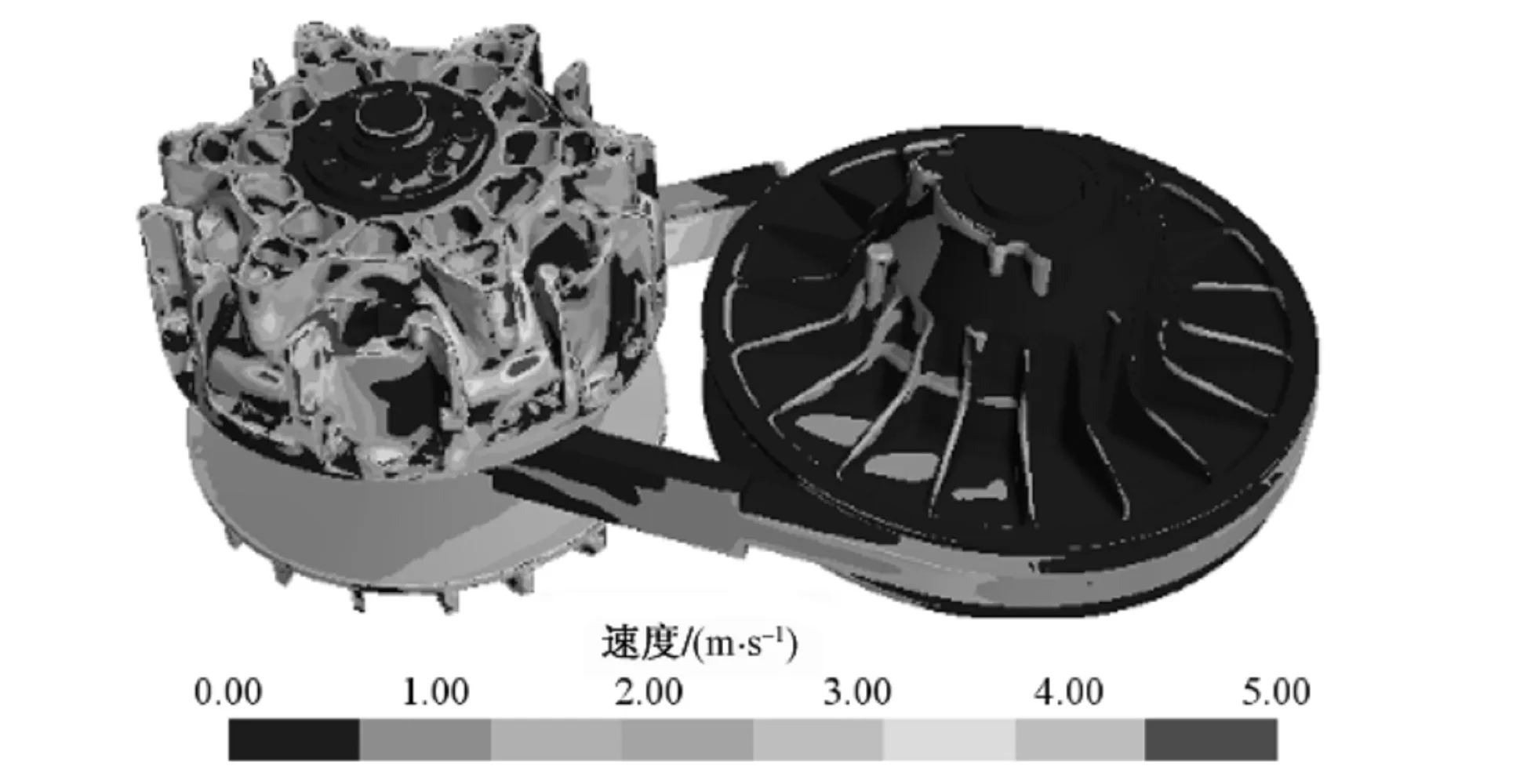
(b) 设计方案二图6 大传动比状态下传动箱内部件表面风速的分布云图Fig. 6 Surface velocity distribution of internal parts of transmission case at big transmission ratio state

从图5可以看出，小传动比时，设计方案二中主动轮表面灰度最大的区域面积比设计方案一略有减小，表示风速低的区域面积减小；设计方案一中传动带上的风速分布集中在12～24 m/s的范围内，设计方案二中传动带上的风速分布则集中在24～36 m/s的范围内，表明设计方案二中传动带表面的风速比设计方案一有明显提升，有利于传动带的冷却，延长其使用寿命，同时从动轮表面风速对应速度标尺 “60”的区域面积也略有增大。综上所述，设计方案二的传动带表面风速和从动轮表面风速分布略优于设计方案一。

从图6可以看出，大传动比时，设计方案二中传动带表面风速的分布集中在1～2 m/s的范围内，设计方案一中传动带表面风速的分布集中在0～1 m/s的范围内；设计方案二比设计方案一中从动轮表面风速较大的区域面积稍大。总体来说：大传动比状态下，设计方案二的主动轮表面风速与设计方案一中主动轮表面风速相当；设计方案二的传动带表面风速略优于设计方案一。

3.4 传动箱内风的速度流线

传动箱内风的速度流线在小传动比状态下和大传动比状态下相似，因此这里仅选择小传动比状态下传动箱内风的速度流线(图7)，进行两种设计方案的对比分析。

(a) 设计方案一

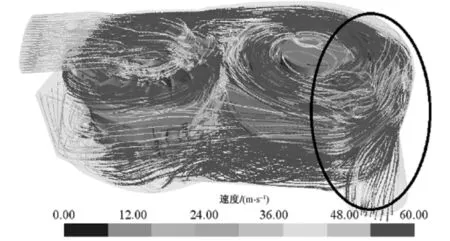
(b) 设计方案二图7 小传动比状态下传动箱内风的速度流线Fig. 7 Velocity streamline distribution in transmission case at small transmission ratio state

相比设计方案一来说，设计方案二对出风口位置进行了调整，让进风口与出风口存在一定的高度差，使得从入口进入的气流流动路径变长，冷却风的利用率变大，避免了设计方案一中“风从入口进入后直接从出口流出”的不合理现象。分析可知，传动箱冷却结构设计方案二进风口面积增大及出风口位置调整，使得总风量增大、冷却风利用率提升，有利于传动箱内部件的冷却，能延长关键零部件的使用寿命。

4 结语

本文采用CFD方法对发动机传动箱冷却结构两种设计方案下的总风量、表面风速分布及风的速度流线进行了对比分析。设计方案二由于在设计方案一的基础上适当增大了进风口面积并改变了出风方向，在小传动比状态下总风量比设计方案一增大约20.9 g/s，风量增加比例约为21%；在大传动比状态下总风量比设计方案一增大约10.7 g/s，风量增加比例约为65%。从表面风速的分布情况来看，设计方案二的传动箱内部件(主动轮、从动轮及传动带)的表面风速分布在小传动比状态下和大传动比状态下均优于设计方案一，且设计方案二改变出风方向后，冷却风的利用率提升，避免了设计方案一中“风从入口进入后直接从出口流出”的不合理现象。研究结果可为传动箱冷却结构设计及冷却性能评价提供理论参考和数据支撑。