隔板对街道峡谷内污染物扩散的影响

贺广兴 ,王 润 ,曾国梁

(1.湖南人文科技学院 能源与机电工程学院,湖南 娄底 417700;(2.中南大学 环境学院,湖南 长沙 410083)

随着我国城市的发展,城市内部的空气污染变得越来越严重。城市交通废气的排放对人体健康造成诸多负面影响,尤其在街道两边耸立的高楼形成的街道峡谷中,污染物更加难以扩散。风洞实验和CFD 模拟是研究街道峡谷污染物扩散的两种主要手段[1-5]。

大气状况和城市的整体布局是影响城市通风及污染物扩散的宏观要素。而对于城市内部的街道峡谷而言,街道长径比例[6]、风速及风向[7]、温差浮力[8]、峡谷结构[9]、屋顶结构[10]、建筑高度变化[11]、街道内部植被[12]、高架桥[13]、广告牌[14]等是影响峡谷内部空气流场和污染物扩散的主要因素。

现有文献资料中,还没有查阅到挡板的设置对街道峡谷内部污染物扩散的影响,因此笔者首次研究不同位置的设置挡板对街道峡谷内部气流组织及污染物扩散的影响程度。

1 模型建立

1.1 控制方程

本研究采用现有资料中普遍采用的标准k-ε模型[7],控制方程如下:

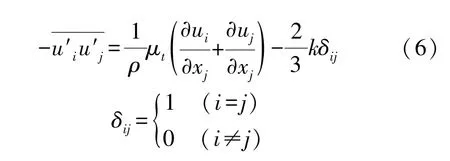
式中:ui——流体速度在i方向上的分量;uj——流体速度在j方向上的分量;xi、xj分别为i、j方向上的坐标;ρ——流体密度;p——流体压强;gi——重力加速度;v——流体运动粘性系数;μ——流体动力粘度;μt——流体湍流黏性系数;k——湍动能;ε——湍动耗散率;t——时间;Gk——湍动能产生源项;Di组分分子扩散率;Ci气体组分浓度;Sct——湍流施密特数;σk、σε——湍流Prandtl 常数;Cε1、Cε2——模型常数;δij——Kronecker 符号。

1.2 计算区域、网格划分及边界条件

1.2.1 模型计算区域

图1(a)、图1(b)分别表示参考模型(不设置挡板)和对照模型(设置挡板)的计算区域示意图,内部空气视为不可压缩气体,由于太阳辐射引起的浮力影响不予考虑。街道峡谷模型的街道宽度(B)和建筑高度(H)分别设为为0.06 m;宽为0.01 m 和高为 0.001 2 m 的线污染源布置在街道中心位置。CO 和空气的排放浓度分别设置为Qco=1×10-7m3/s、Qair=3×10-5m3/s。0.001 m 宽和0.01 m 高的挡板分别设置在离屋顶不同距离的位置,如图1(b)所示,ΔL分别设置为0.005 m、0.007 5 m、0.01 m、0.012 5 m、0.015 m、0.02 m、0.03 m,分别定义为case2、case3、case4、case5、case6、case7、case8。

图1 模型计算区域及网格化

1.2.2 网格划分

计算区域的结构化网格划分如下:挡板边界统一划分为0.001 m;气流区域下部边界划分边界层,第一层边界为0.000 5 m,扩展比例为1.15,边界层网格为10 层;街道峡谷内部网格统一划分0.001 m。无挡板和有挡板情况下,整个计算区域网格数分别为31 680 和316 70。

1.2.3 边界条件

参考其他学者的相关研究文献[15],此次模拟的入口边界条件如下:

式中:Z——距离地面高度;u(z)、k(z)、ε(z)——分别为在Z高度位置的水平风速,湍动能和耗散系数;zref——整个计算区域高度;uref——参考风速;u*(0.325 m/s)为摩擦速度;K(=0.4)为冯.卡门常数;Cμ=0.09;出口边界条件设置为0 压力梯度;上边界为对称边界条件,其他边界为无滑移边界。

2 模型验证

CFD 模拟结果的可靠性利用Meroney 的风洞实验进行验证[16]。在此风洞实验中,街道峡谷模型中的建筑高度和街道宽度分别为0.06 m;0.01 m 宽和0.001 2 m 高的发射污染物(乙烷)和空气混合气体的线源布置在街道中心位置,风向垂直于街道,气体污染物浓度测量点布置在街道旁建筑的两侧及屋顶,模型示意图如图2 所示:

图2 风洞实验模型

风速入口边界条件参照原实验,计算式如下:

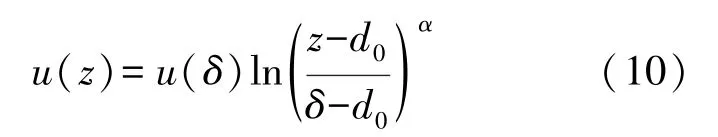
式中:d0=2 mm;u(z)——z高度处的风速;u(δ)——高度0.5 m 处的平均风速;(δ=0.5 m);指数α=0.28。

污染物浓度归一化处理[26]:

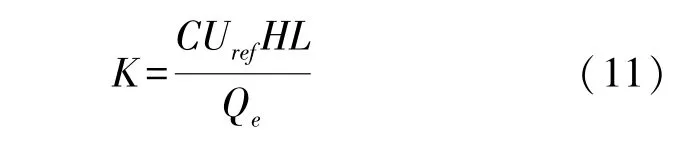
式中:C——乙烷体积浓度;Uref——参考风速,m/s;H——建筑高度,m;L——线源长度,m;Qe——污染物散发源强,m3/s。

模拟结果和实验结果对比结果如图3 所示,可以看出整体吻合情况良好,迎风面的吻合程度很好,实验数据和模拟数据基本重叠。背风面趋势吻合程度较好,中间有一个模拟数据高于实验数据,下部一个模拟数据略低于实验数据。

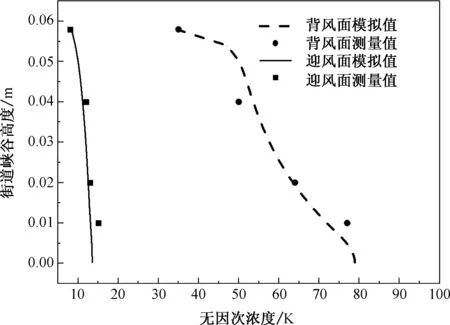
图3 模拟值与实验测量值对比

3 结果及讨论

3.1 峡谷内部流场分布

图4 展示了挡板放在不同位置街道峡谷内部流场的变化情况。图4(a)为没有挡板的情况,由于风速切应力的影响在峡谷内部形成了一个主要的、大的顺时针涡旋,空气在峡谷内部流动,此种情况不利于污染物的扩散;整个峡谷内部的速度处于低速状态;图4(b)为挡板放置在离风速来流方向的屋顶0.005 m 处时街道峡谷内部的风速流场。由于挡板的影响,峡谷内部的空气流场发生了很大的变化,内部形成主要的逆时针涡旋,涡旋外部空气从左边入口进入,在右侧区域离开了峡谷,较高的风速出现在入口处。可知,此种流场较图4(a)的流场而言,有利于无污染的扩散,峡谷内部污染物可随流场扩散到峡谷外部,有利于降低内部污染物浓度。图4(c)为挡板放置在离风速来流方向的屋顶0.075 m 处时街道峡谷内部的风速流场。由图可知,风速较大区域出现在入口处,由上述分析可知,此种情况比较有利于污染物的扩散。图4(d)为挡板放置在离风速来流方向的屋顶0.075 m 处时街道峡谷内部的风速流场。可以看出,峡谷内部流场和风速分布发生了较大的变化,在峡谷底部形成了一个顺时针涡旋。峡谷上部空气从入口进入,然后从右侧离开了峡谷,较大风速带出现在峡谷上部分区域。分析可知,由于下部形成了涡旋,污染物在峡谷的底部区域不易扩散,而上部分由于空气离开了峡谷,有利于污染物的扩散。图4(e)～图4(h)分别为挡板处于0.012 5 m、0.015 m、0.02 m、0.03 m 位置时街道峡谷内部的风速流场。由图可知,后面几种情况下峡谷内部的流场分布与图4(d)流场基本类似,区别在于随着挡板放置位置距离的增大,峡谷下部分涡旋所占的区域面积越大,涡旋所在区域不利于污染物的扩散。

图4 街道峡谷内部流场及速度分布

3.2 峡谷内部无因此CO 浓度分布

不同挡板设置条件下街道峡谷内部无因次化CO 浓度分布情况如图5 所示。由图5 可知,在无挡板下,峡谷内部CO 集中在峡谷的左边,右边的浓度相对比较低。此种现象是峡谷内部的主要顺时针涡旋,导致污染物随空气流在峡谷右侧聚集。图5(b)为挡板设置在离屋顶0.005 m 处,此种条件下,CO 主要集中在峡谷右侧区域,这是挡板的存在,峡谷内部形成逆时针涡旋,导致污染物随空气流向峡谷右侧聚集,但是涡旋外部气流在右侧流出了峡谷,因此可以带走部分CO,所以此条件下整体浓度相比图5(a)有所下降。图5(c)挡板设置在0.007 5 m 处,由图可知,此种情况峡谷内部CO 由于逆时针的气流作用在峡谷右侧聚集,但是整体浓度又有了进一步的降低。图5(d)为挡板设置在0.01 m 处,高CO 浓度发生在峡谷的下部,峡谷上部分CO 浓度较低。这是下部分形成了涡旋,导致污染物难以扩散出峡谷,气流穿过了上部分峡谷,造成上部分CO 随气流被带离了峡谷。图5(e)～ 图5(h)分别为挡板设置在0.012 5 m、0.015 m、0.02 m、0.03 m 位置,无因次CO 浓度整体分布情况与图5(d)类似,峡谷下部分浓度高,上部分较低,随着挡板设置的距离增大,峡谷下部分高浓度区域所占面积越来越大,这是挡板设置距离的增大,造成峡谷下部分的主涡旋增大,从而导致高污染物浓度区域面积增大。

图5 无因次CO 浓度分布

3.3 峡谷内部平均无因次CO 浓度

挡板布置在不同位置时街道峡谷内部CO 的平均无因次浓度分布如图6 所示。由图6 可知,整体分布呈现V 形,在无挡板时,平均无因次CO浓度为31.49,随着挡板的设置,浓度下降显著。挡板位置在0.005 m 处时,平均无因次CO 浓度为21.38,较开始下降了32.1%;挡板位置在0.075 m处时,平均无因次CO 浓度为16.41,较开始下降了47.9%;后面随着挡板距离的增加,平均无因次CO 浓度反而上升。由此可知,挡板处于0.007 5 m处对峡谷内部的污染物扩散最为有利。

图6 街道峡谷内部平均无因次CO 浓度值

4 结论

通过模拟不同挡板设置对街道峡谷内部流场及污染物浓度扩散的影响分析,可得出以下结论:

(1)挡板的设置对街道峡谷内部流场影响显著。当设置距离逐渐增大时,峡谷内部的流场变化由单个主涡旋,逐渐演变流场呈现为上下分层现象。下部分形成一个主要的涡旋,峡谷上部分气流穿过了峡谷。

(2)挡板对街道峡谷内部污染物影响明显。设置距离偏小时,污染物由向背风侧逐渐在迎风侧聚集,导致迎风侧浓度升高;随着设置距离的增大,污染物浓度分布也出现上下分层现象,下部分涡旋导致浓度高,上部分由于气流的稀释作用,浓度降低。

(3)峡谷内部污染物的平均浓度与挡板的设置距离相关,合理的设置位置可以显著降低街道峡谷内部污染物浓度。