水下爆破动水压力预测及衰减规律研究

张天宇

（1.中铁第一勘察设计院集团有限公司，陕西 西安 710043；2.陕西省铁道及地下交通工程重点实验室，陕西 西安 710043）

在邻近或下穿江、河、湖、海的城市地下交通、能源运输等工程建设中，大多数工程都面临岩体或基岩侵入建筑限界的问题。对于此类问题，目前常以水下钻孔爆破作为炸礁清航类工程的主要技术手段。

水下钻孔爆破相对于陆地钻孔爆破理论发展较晚，且二者工况环境大不相同，因此陆地钻孔爆破理论成果很难完全适用于水下钻孔爆破实践。同时水下钻孔爆破与陆地钻孔爆破所产生的危害不同，水下钻孔爆破的危害主要是爆破诱发的振动效应与水击波压力协同响应。近年来，水下钻孔爆破施工所诱发的各种效应备受国内外学者关注[1-6]。詹发民等采用自主研发的水下爆破振动监测系统进行现场监测，利用小波包分解获得振动信号不同频带的能量分布情况[7]。陈泉等以水下钻爆开挖产生的振动效应为研究对象，通过现场监测和分析得出了水下爆破振动激励下附近建筑物的结构响应特性并提出了相应的控制措施[8]。邵蔚等通过修正水下爆破振动速度公式，并利用傅里叶变换分析得出水下爆破具有明显的滤频效应[9]。苏欣通过对水下爆夯进行现场实时监测，并对水下爆破冲击波信号进行时频分析，初步得到了水下爆破冲击波强度随距离的变化关系[10]。曲艳东等利用仿真软件模拟水下爆破破冰过程中冲击波压力的作用特征，发现了在冰体覆盖的相对封闭条件和常规水下爆炸时水中冲击波压力变化的差异性[11]。张树洪等以海底爆破工程为基础，通过对现场监测数据的分析研究发现海底爆破所诱发的振动会对海洋生态环境和海洋生物造成影响[12-14]。

上述学者大多是从水下爆破振动效应和水冲击波压力角度展开研究，忽视了水下爆破振动所诱发的动水压力效应。与陆域爆破危害不同，水下钻孔爆破的危害主要是振动效应与水击波压力协同响应。当水下爆破的被爆岩体上方存在较厚的海底覆盖层，且装药堵塞后可近似不存在临空面时，爆破所释放的绝大部分能量会被岩体和海底覆盖层吸收，因此在这种工况下，本文认为水介质中的冲击波主要为爆破振动效应传播至海底覆盖层与水介质两种界面所诱发的动水压力效应，然而目前针对此工况下所诱发的动水压力效应研究相对匮乏。

本文以厦门市轨道交通3 号线本岛至翔安海底隧道工程建设项目为背景，综合分析水下爆破所诱发的动水压力峰值的影响因素，建立动水压力预测模型，并探明动水压力的衰减规律，研究成果将进一步完善水下钻孔爆破理论，以期为日后类似工程实践提供理论参考。

1 基本理论

目前，对于动水压力的预测，普遍采用美国学者Cole 等根据以往水下爆炸相关理论与试验研究所提出的水击波压力峰值公式[15]：

式中：P 为水击波压力峰值，单位为MPa；Q 为单段最大装药量，单位为kg；R 为测点到药包中心的直线距离，单位为m；k 为与爆破场地条件有关的参数；α 为衰减系数。

根据公式（1）可知水下钻孔爆破所诱发的动水压力峰值受测点到药包中心的直线距离、单段最大药量及场地条件等因素的影响，且该公式是建立在水下裸爆的基础上，若仍采用该公式对动水压力峰值进行预测，势必会产生一定的偏差。因此，为更科学、更准确地预测水下钻孔爆破所诱发的动水压力峰值，本文采用量纲分析法对传统的Cole 公式进行修正。

陆域爆破施工过程中，爆破参数、介质参数、炸药参数及地质条件等因素都会影响爆破所诱发的各种效应传播速率[16-17]。因此，类似陆域爆破可将影响水下钻孔爆破所诱发的动水压力效应变化（即动水压力峰值P）的物理量总结概括为15 个（表1）。

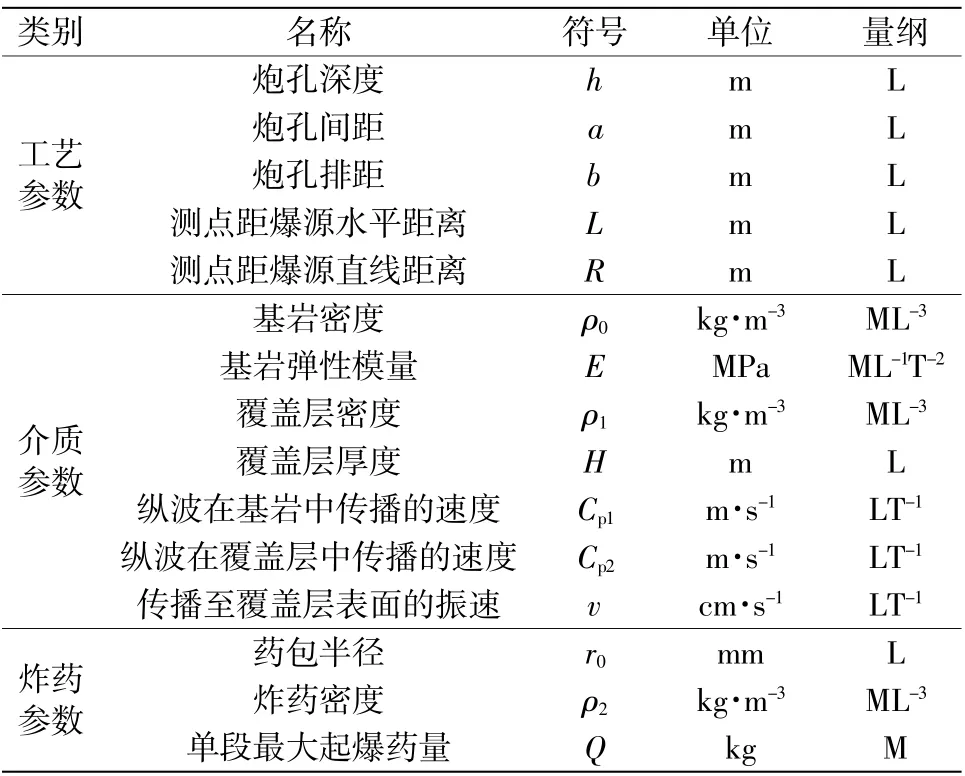
表1 影响水下钻孔爆破动力压力峰值的物理量参数表

基于量纲分析的π 定理，任一物理量x 的量纲公式可以用基本量纲的指数乘积形式来表示[18]，选取L、Q、Cp1作为独立量纲，将影响动水压力的函数模型用由15 个独立参量组合成的12 个无因次数组πi（i=1～12）之间的函数关系来表示：

因此相似标准方程可写成：

从公式（3）可以看出，要想构建完整的相似准数方程十分复杂，需要在同种工况下进行多次爆破试验才能得出相应的准数方程。在这种情况下，由于海底覆盖层和基岩经过多年的沉积，区域内物理性质变化不大。同时每次爆破施工采用的工艺参数和炸药种类相同，因此根据量纲分析法的和谐原理及不同无因次量π 的乘积或商比仍为无因次量，该公式可简化为：

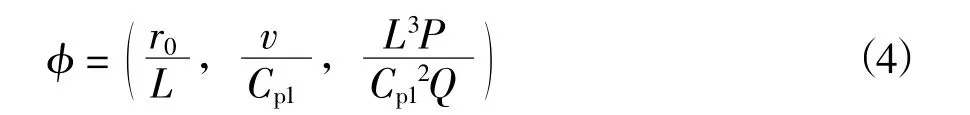
在炸药种类不变的条件下，装药半径和装药量之间存在三次函数的关系[19]，即r0≈Q1/3。且对于某一具体工程场地，Cp1可以近似为常数，因此将公式（4）按照指数函数泰勒展开化简可得动水压力预测模型：

式中：β 为与地质条件、工艺参数有关的相关系数，其余各参数含义与上述相同。

2 工程实例

2.1 工程概况

厦门市轨道交通3 号线本岛至翔安海底隧道位于厦门本岛的东北方位，左右线长分别为1415.218 m和1419.928 m，其中海域段为1.1 km，其走向如图1 所示。海域段隧道盾构施工段中的基岩突起段为花岗闪长岩，洞身范围内基岩面凸起变化较大，施工段中的碎裂强风化带、中等风化带较为薄弱，其中突起段主体为微风化基岩，其基岩凸起情况及基岩取芯情况分别如表2 和图2 所示，因此为避免施工过程中盾构轴线发生偏移、刀盘道具严重磨损，以致于造成严重的经济损失，故对侵入隧道断面的基岩进行超前爆破破碎处理。

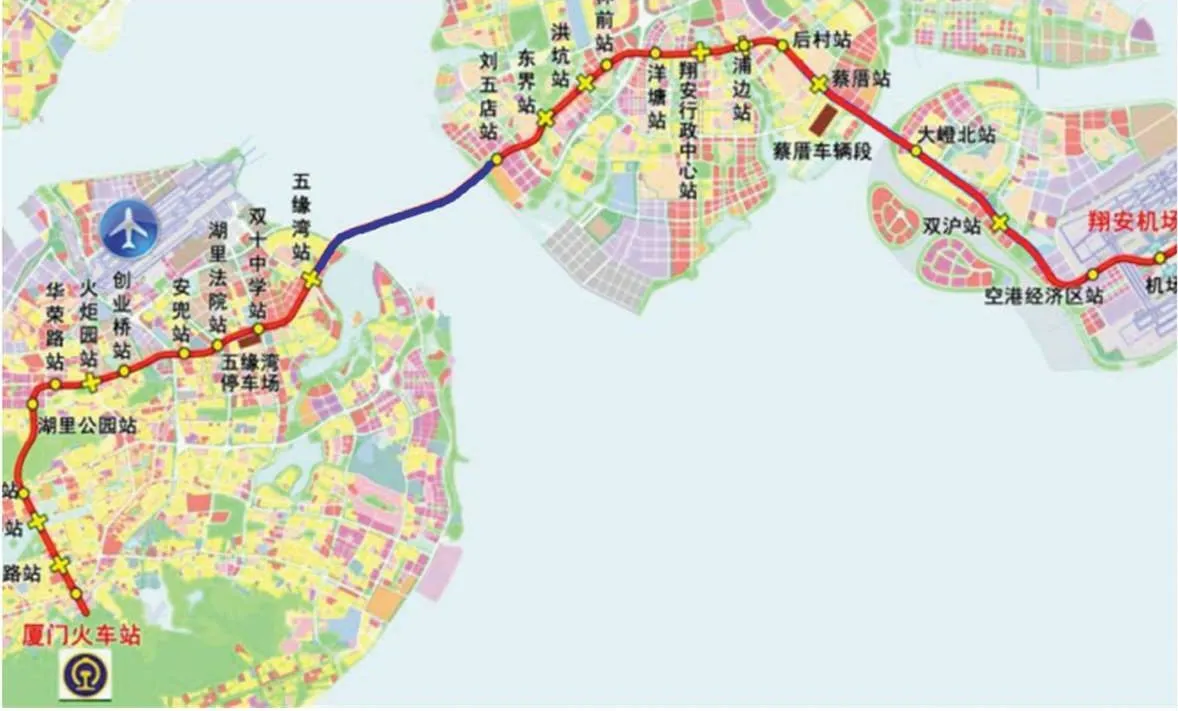
图1 厦门市轨道交通3 号线工程线路图

图2 突起基岩岩体取芯图

表2 海域段突起基岩岩体分布情况 单位：m

2.2 爆破施工及现场监测

海域段隧道施工区域水深在10～20 m，海底覆盖层厚度在25～40 m。该海域为中华白海豚、文昌鱼等海洋生物的自然保护区[20]，因此在保证基岩破碎程度满足要求的前提下，必须要最大限度地减小爆破施工作业对海洋生物的危害。

爆破施工采用水胶炸药、配套塑料导爆毫秒雷管和毫秒电雷管及高能电容式起爆器，药卷直径100 mm，长度50 cm，每卷4 kg，孔间排距为1.2 m×1.2 m，炮孔直径为146 mm，炮孔布置如图3 所示。

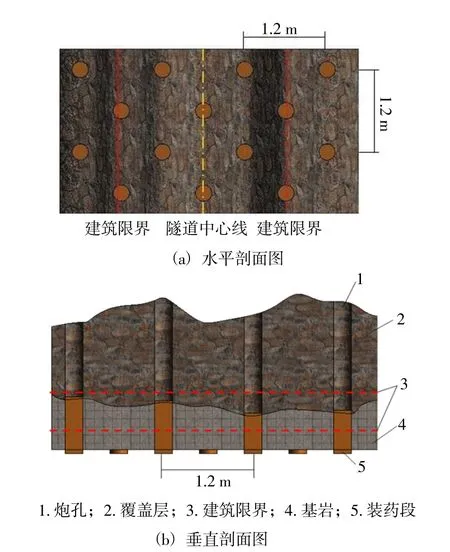
图3 炮孔布置图

由于水下监测环境复杂且难度较大，不宜同时大范围、长距离布置监测点，故采取“多监测、少布点”的监测原则。同时根据量纲分析法修正得到的动水压力预测模型（即公式（3））可知动水压力峰值与振速有密切关系，因此针对爆破振动和动水压力峰值现场监测试验分别布置2 个监测点，监测仪器在船甲板连接好后，将三矢量振速传感器施加特定配重装置后缓慢沉入水底至覆盖层表面，同时打开动水压力传感器的保护盖，并施加特定配重装置后沉入水下5m 处。振动监测仪器及动水压力仪器安装和测点布置示意图分别如图4、图5 所示。

图4 爆破振动仪器安装和测点布置示意图

图5 动水压力仪器安装和测点布置示意图

由于海水流动冲击的影响，不能正常布置传感径向和切向的指向，故提取传感器垂向监测数据作为研究对象，因本次现场试验监测次数较多，下面仅列举具有代表性的爆破振动波形图和动水压力峰值图（图6），并将试验数据整理汇总为表3。

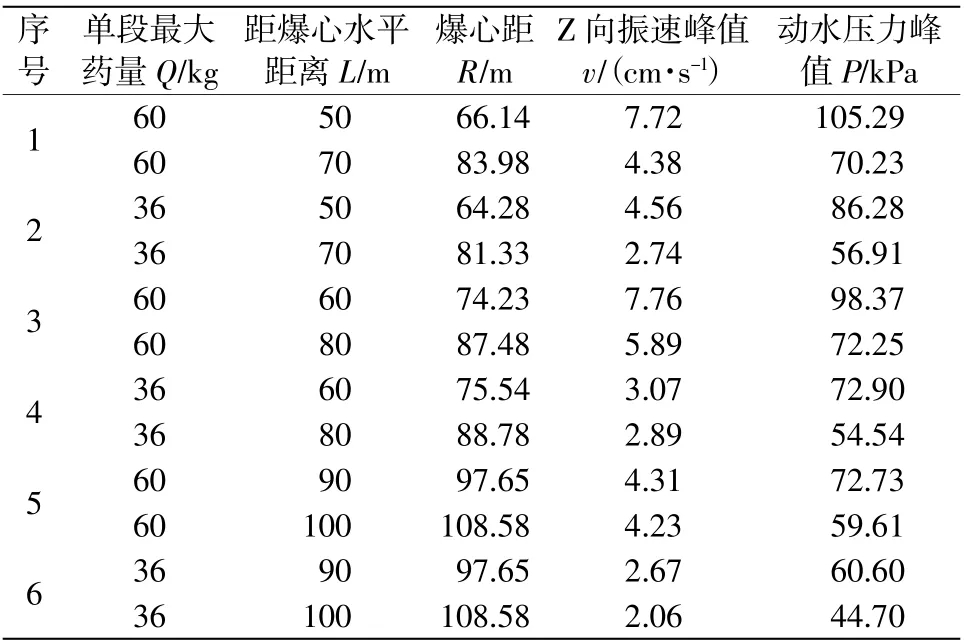
表3 动水压力监测数据

图6 爆破振动波形图和动水压力峰值图

3 信号分析

3.1 监测数据回归分析

传统的Cole 动水压力峰值公式及根据量纲分析法修正得到的公式均需要通过回归运算获取公式的相关参数。依据监测所得的数据，应用Matlab软件对上述模型公式进行非线性回归运算分析，从而得出相关参数值，如表4 所示，两种模型公式的非线性回归分析分别如图7 和图8 所示。

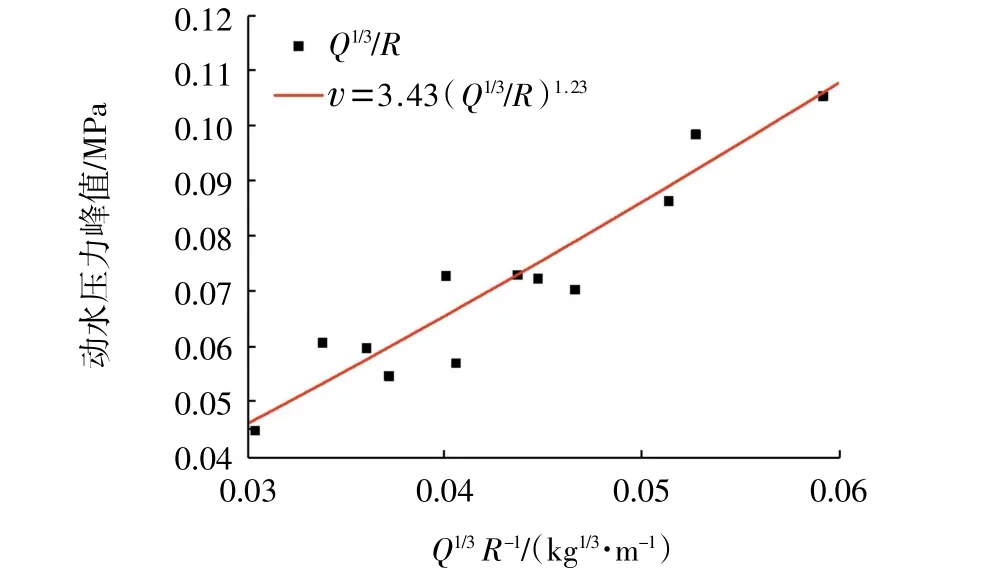
图7 Cole 动水压力公式非线性回归分析图

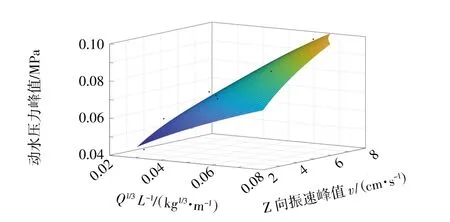
图8 公式（5）非线性回归分析图

表4 回归参数表

因此可得公式（1）为：

公式（5）为：

3.2 非线性回归分析准确度评价

海底钻孔爆破所诱发的动水压力效应传播过程较为复杂多变，非线性回归运算结果必然存在一定误差。为验证量纲分析法建立的预测模型的适用性和非线回归运算的准确度，应用得出的公式（6）和公式（7）对监测数据进行相对误差分析。ε 为相对误差，ε=|v预-v实|/v实，相对误差计算结果见表5 所示。

从表4 中的r 值可以看出，传统Cole 公式和修正得到的公式（5）非线性回归运算都比较准确，但修正得到的公式（5）相比传统Cole 公式对数据贴合度更高。从表5 可以看出，非线性回归运算得到的公式（6）和公式（7）对动水压力峰值预测都较为准确，二者相对误差区间分别为0.64%～17.11%和0.08%～6.53%，平均相对误差分别为7.31%和3.33%。因此，相对误差分析的结果证明了采用量纲分析法修正得到的动水压力模型预测更接近于实际，也说明采用特定配重固定装置的三轴矢量振速传感器及动水压力传感器对信号进行采集的准确性；同时证明了修正得到的模型公式可应用于工程实践，且比传统的Cole 经验公式更为准确。

表5 相对误差计算结果表

3.3 动水压力衰减规律分析

根据修正得到的动水压力预测模型可以发现，海底爆破所诱发的动水压力效应主要同单段最大药量、监测点距爆心水平距离及传播至覆盖层表面的振速峰值有着密切关系，为探明这些影响因素对动水压力峰值的影响程度和影响效果，依据经非线性回归运算得出的公式（7）绘制图9、图10。

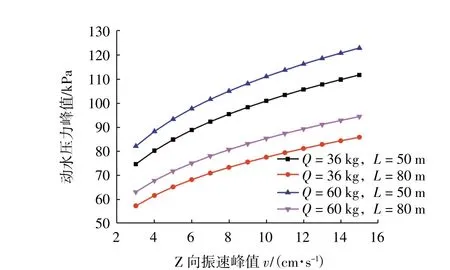
图9 动水压力峰值与覆盖层表面Z 向振速峰值关系图

图10 动水压力峰值与距爆心水平距离关系图

上图表明：①单段最大药量对动水压力峰值的影响最为明显，同时传播至覆盖层表面的振速峰值大小和距爆心水平距离大小对动水压力峰值的影响也较为明显；②动水压力峰值随着单段最大药量的增加而增大，随着传播至覆盖层表面的振速峰值的增大而增大，随着距爆心水平距离的增大而衰减。

依据费鸿禄等针对海底爆破振动速度峰值的研究成果可知，海底爆破振速峰值的大小与多影响因素有关，其中单段药量的增加是使传播至覆盖层表面的振速峰值增大的主要原因，同时振速峰值随着传播距离的增加而不断衰减[21]。因此可认为出现上述现象的原因是：爆心附近区域的振动效应较大，且振动效应强弱主要受单段最大药量影响，从而爆心附近由振动效应传递至海水介质所诱发的动水压力效应也越强烈；但随着传播距离的增大，在海水介质中传播的动水压力峰值不断衰减，同时传播至覆盖层表面的振动效应所携带的能量不断衰减，继续诱发的动水压力效应强度也不断衰弱。

4 结论

（1）运用量纲分析法建立水下爆破所诱发的动水压力相似准数方程，并对现场监测的数据进行非线性回归分析，得到水下爆破条件下所诱发的动水压力峰值预测模型。

（2）对新建预测模型和传统的Cole 动水压力公式进行准确度评价分析，二者相对误差范围分别为0.08%～6.53%和0.64%～17.11%，平均相对误差分别为3.33%和7.31%，证明了新建模型预测的准确性及应用于工程实际的可行性。

（3）现场监测数据和分析均表明，水下爆破所诱发的动水压力效应与单段最大药量、距爆心水平距离及传播至覆盖层表面的振速峰值有密切关系：动水压力峰值随着单段最大药量的增加而增大，随着传播至覆盖层表面振速峰值的增大而增大，随着距爆心水平距离的增大而不断衰减。