套筒对波流作用下桩基局部冲刷防护试验研究

罗巍，程永舟，2，黄筱云，2，王晓光

（1.长沙理工大学水利工程学院，湖南 长沙 410114；2.水沙科学与水灾害防治湖南省重点实验室，湖南 长沙 410114）

桩基础作为一种结构简单、承载力强、适用范围广的基础形式，在海洋工程中应用广泛[1]。海洋环境中的结构物桩基础同时受到波浪和水流的作用，其周围会发生局部冲刷现象，使得桩基自由长度增大，对近海结构物的稳定性造成影响[2]。在海洋环境中，水动力条件复杂多变，难以准确预测桩基周围的最大冲刷深度[3]，需要考虑采取一定的冲刷防护措施。

几十年以来，已有众多学者针对纯流条件下的冲刷防护进行了研究，并提出了多种类型的防护措施。这些防护措施主要可分为两类[4]，一类是床面加强措施，即直接对床面材料进行加强改造的措施，如抛石防护、土工袋防护、石笼防护等。Chiew 对抛石护底抗冲措施的结构和破坏机理进行了分析[5]。Zarrati 等采用抛石与护圈组合防护的方式，对防护下单桩和双桩的局部冲刷特性进行了研究[6]。付旭辉等分析了钢丝石笼防护下的冲刷机理，研究了钢丝石笼在不同水流环境中的防护特性[7]。高正荣等采用抛填沙袋与下沉护坦相结合的方式对苏通大桥进行了冲刷防护，并研究了大型桥梁冲刷防护工程的损坏特性[8]。Huang 等研究了柔性混凝土软体垫的冲刷防护特性[9]。另一类是水流控制措施，其防冲原理是扰乱来流，削弱马蹄涡等引起冲刷的水力因素。Grimaldi 等提出可以在桩后布置横向平板作为拦沙槛，限制桩后尾涡的发展范围，阻止泥沙被水流带向下游，并验证了其作为冲刷防护对策的有效性[10]。陈兵等通过放置扰流环来削弱马蹄涡，以减小桩周局部冲刷深度[11]。Somayeh 等利用喷射水流干扰桩前来流以减小冲刷，验证了该防冲措施的有效性[12]。姜松等采用桩前减冲桩作为防护措施，研究其防冲效果及桩柱周围的流场特性[13]。Elnikhely 等研究了圆形开孔对桩基冲刷防护的作用[14]。Bestawy 等研究了不同桩身开槽方式及护圈型式组合下的防冲效果[15]。Zhang等在纯流条件下讨论了护筒直径、埋置深度及水流强度对护筒防冲效果的影响，并与护圈防护进行了对比分析[16]。

床面加强措施在工程中应用广泛，但使用寿命一般较短，比如抛石防护，当水流流速比较大时，防护块石容易流失，导致防护效果逐渐减弱。水流控制措施大多受到水流流向的限制，当流向发生摆动时防冲效果较差，比如当桩身开缝与水流夹角大于45°时，便会失去防护效果[17]。此外，目前该类措施的研究大多局限于单向恒定流条件，其在波流环境中是否具有同样的防护效果，仍未得到更深入的研究。

防冲套筒是一种简单的防护结构，在桩柱周围布置套筒，可以限制马蹄形旋涡的发展空间，并将桩基周围大部分床沙的活动范围限制在套筒内部，从而减少冲刷[18]。套筒防护不受水流流向的限制，能够适用于各种水流条件下的冲刷防护。Liang 等对比研究了包括套筒在内的4 种防冲措施在波流条件下的防冲效果，发现大多数水流控制措施在波流作用下防冲效果较差，甚至产生了更深的冲刷坑，而套筒防护在波流作用下仍具有一定防冲能力，但其针对套筒防护的试验工况较少，缺少对套筒防冲效果影响因素的研究分析[19]。本试验分别在纯流及波流作用下探讨了套筒的防冲性能，进一步分析套筒高度和直径对冲刷的影响，提出最佳的套筒布置方式，为实际工程提供参考。

1 试验布置及试验工况

1.1 试验布置

试验在长沙理工大学水利实验中心的波流水槽中进行。水槽长45 m，宽0.8 m，高1 m，工作水深0.2～0.7 m。水槽设有循环造流系统并配备有沉淀池。试验沙槽位于水槽中部，长3 m，宽0.8 m，高0.6 m，内部铺满中值粒径d50= 0.406 mm 的无黏性沙，沙槽正中央埋放直径D = 0.05 m 的模型圆柱，套筒埋置在沙床中，沙槽上下游底床均为砂浆抹面，水槽侧面为玻璃边壁，水流到达桩前可形成稳定的流速剖面。试验水深h = 0.4 m，大于3～4 倍桩径D，此时可忽略水深对于冲刷的影响[20]。波高测量采用WG50 型浪高仪，流速测量采用三维点式多普勒流速仪（ADV），地形测量采用ULS-100 型水下激光三维地形扫描仪。由于水槽宽度B 有限，必须控制模型的尺寸来防止边壁效应。参考Whitehorse[21]的建议，在清水冲刷条件下，水槽宽度与模型尺寸比值B/D 应大于6。采用1.25D、1.5D、1.75D、2D 四种直径的套筒进行防冲试验，B/D 最小值为8，可忽略边壁效应。根据王顺意等[22]以及本文预试验的结果，当局部冲刷坑发展充分时，桩周最大冲刷深度始终出现在桩柱正前方，故设套筒内桩正前方、套筒外筒正前方两个位置作为特征点进行观测，两个观测点的冲刷深度分别用以表示筒内桩周围和套筒外周围的最大局部冲刷深度。桩身和筒身分别贴有量尺，以测量冲刷深度变化。试验模型布置及观测点位置如图1 所示。

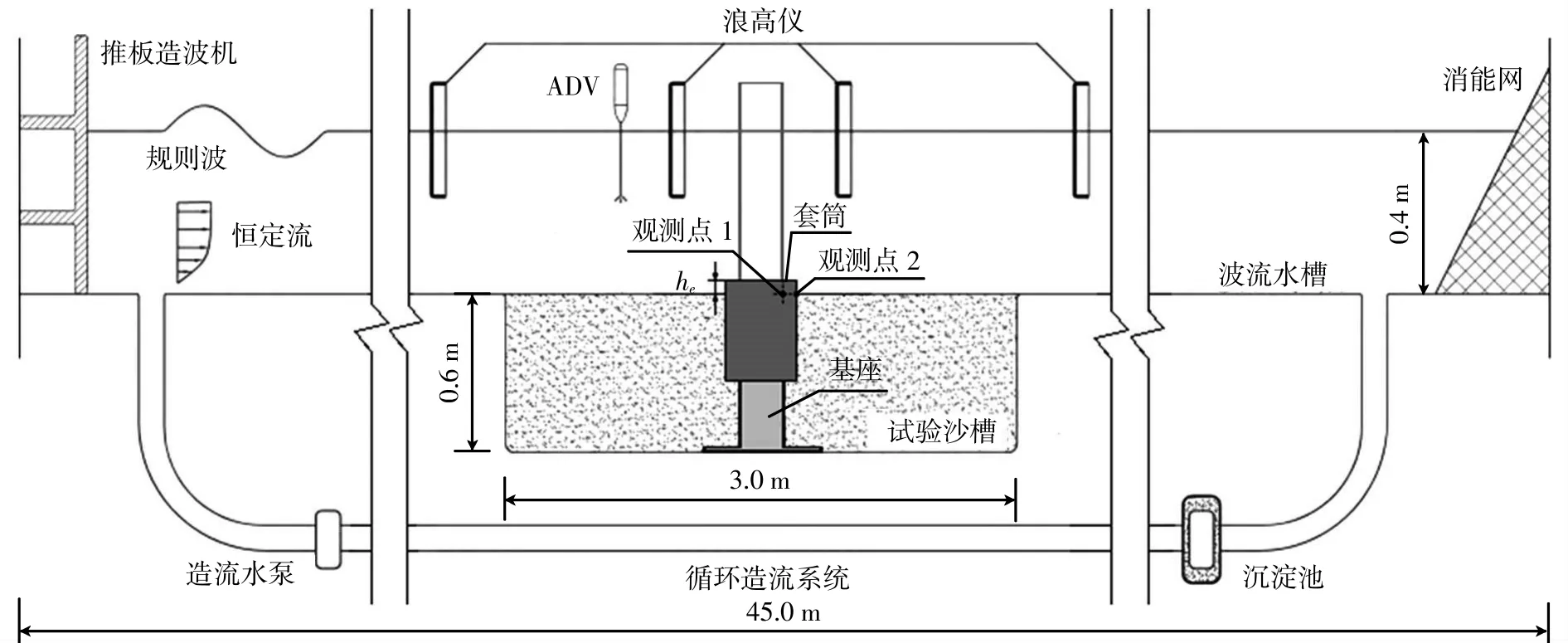
图1 试验布置图

1.2 试验方案

为研究套筒高度和直径对防冲效果的影响，对比分析各试验条件下冲刷过程、冲刷坑形态的差异，设置无防护的垂直桩作为对照组，共开展36组工况试验。试验包括纯流和波流冲刷，以及清水冲刷和动床冲刷。Melville 等提出在室内小型试验中，要达到冲刷平衡，通常需要数天时间[23]。根据预实验和程永舟等[24]的研究结果，当清水组冲刷时间达到6 h 后，冲刷过程虽仍在进行，其规律不再发生较大的变化。本试验仅对各冲刷试验的起始阶段及主要冲刷阶段进行观测，对比分析各组工况在相同冲刷时间内达到的最大冲刷深度，故设清水组冲刷时间为6 h。动床组冲刷过程较快，预试验结果表明动床组冲刷在4 h 内已达到动态平衡（图4），此时桩前床面向下游稳定输出泥沙，上游床面平均高程不断降低，该过程持续时间过长时，会产生其他无关变量影响试验结果。此外，分析波流参数对冲刷深度的影响非本文重点，故仅对比不同波流条件下的冲刷坑形态差异，综合以上考虑，将动床组冲刷时间设为4 h。冲刷试验前对水流流速、波浪波高和周期进行标定，并保存相应的标定文件，以计算机控制造流和造波。每组试验先将与各工况对应直径的套筒以相应的初始高度安装在沙坑中，抹平沙床表面，控制水泵将水注入波浪水槽至试验水深0.4 m。试验波浪为规则波，采用间歇式造波法，防止波浪变形。达到设定冲刷时间后，关闭造流、造波系统，采用地形仪测量冲刷后的床面地形。具体试验工况见表1。

定义R 为筒内冲刷深度减小率，R′为筒内外最大冲深减小率。计算公式为：

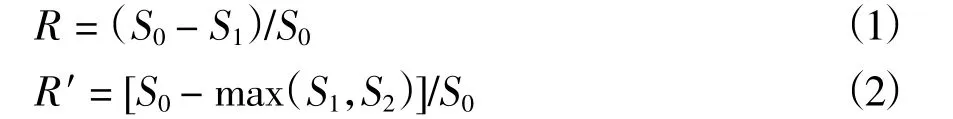
其中S0为无防护下的桩前最大局部冲刷深度。波流共同作用下的希尔兹数θ 和临界希尔兹数θcr计算公式为[25]：

式中：Uf为波流共同作用下的最大摩阻流速；f 为波流共存时的摩阻系数；U0为波流共存时的流速；D*为沙粒量纲粒度；s 为沙水密度比，本试验用沙s=2.65；υ 为运动黏性系数。本试验临界希尔兹数θcr=0.034，当泥沙起动强度θ/θcr＜1 时为清水冲刷，当θ/θcr＞1 时为动床冲刷。根据表1，本试验中C0—C5 工况组为动床冲刷，其余均为清水冲刷。

表1 试验工况

2 试验结果与分析

2.1 冲刷过程

图2 为Ds=1.5D 时，不同套筒高度与纯流条件下，套筒内外相对冲刷深度的历时曲线。从图2（a）的筒内冲深历时曲线可看出，当套筒初始高度较低时，筒内冲刷深度在前30 min 发展迅速。筒内桩前床面先发生冲刷，泥沙在桩后堆积，随后被带出筒外。随着冲刷过程的进行，桩后床面与套筒上边缘逐渐形成高度差，筒内桩后尾涡的能量不足以将大部分泥沙颗粒提升至该高度，无法继续输送筒内泥沙至筒外，致使筒内冲刷速度放缓，120 min 后，冲深历时曲线趋于平缓。根据图2（b）所示的筒外冲深历时曲线，套筒露出高度小时，套筒外水流的流动强度较弱，筒外冲刷强度较小。随着筒外冲刷过程的进行，套筒露出高度逐渐增大，筒前下潜水流、马蹄涡等水力因素亦逐渐增强，冲刷速度随之加快，90 min 左右冲深历时曲线出现拐点。

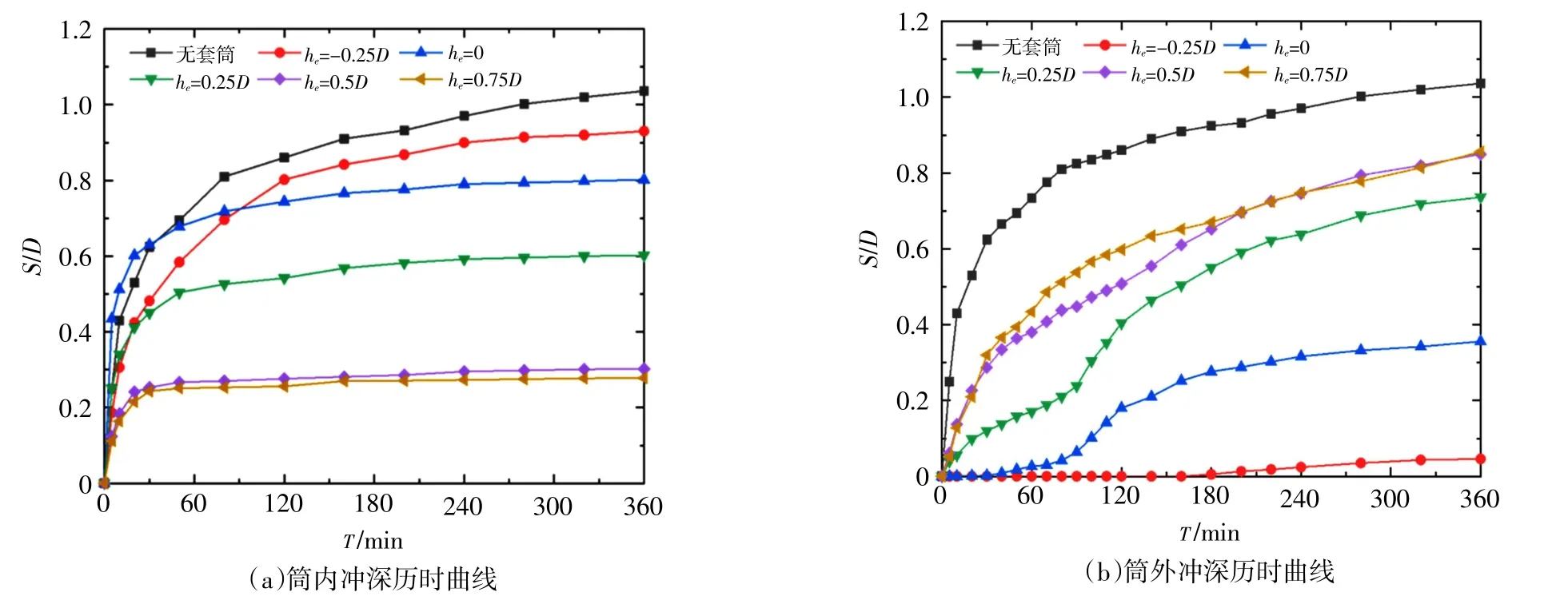
图2 冲刷深度历时曲线（纯流冲刷）

根据图3 的冲刷历时曲线特征，波流条件下的冲刷过程在60 min 前明显加快。波流冲刷过程中，波浪在桩、筒周围的反射、绕射等作用使得筒内外水流的流动强度增大。除下潜水流、马蹄涡的作用以外，还存在波浪对泥沙的上扬力，使桩筒结构附近的床面泥沙更容易起动，故筒外冲刷在初期就发展迅速。

图3 冲刷深度历时曲线（波流清水冲刷）

图4 所示的动床冲刷，由于床面切应力较大，希尔兹数θ 大于临界希尔兹数θcr，床面泥沙颗粒全面起动。如图4（a）、（b）所示，初期筒内外冲刷过程与波流清水冲刷类似，冲刷速度较快。30 min 后，随着床面沙纹发展至桩筒结构附近，大量床面泥沙颗粒被带入冲刷坑，桩前床面对冲刷坑产生净输沙，此时冲刷深度转而减小。由于床面起动具有随机性，沙纹发展至冲刷坑的时间也不具有确定性，但基本发生在60 min 前。90 min 后，整个床面沙纹发展充分，桩前床面向冲刷坑稳定输出泥沙，桩筒结构周围的局部冲刷继续发展，冲刷深度继续增大。240 min 后，冲刷坑内输出和输入的泥沙达到动态平衡，冲刷深度不再发生明显变化。

图4 波流动床冲刷过程

2.2 冲刷坑形态

2.2.1 不同波流条件下的冲刷坑形态对比 图5（a）—（c）为he= 0.25D，Ds= 1.5D 时不同波流条件下的冲刷坑地形图。图5（a）为纯流冲刷，对比图5（b）的波流冲刷地形图可看出，纯流条件下，套筒内外的冲刷深度和冲刷范围均较小，冲刷坑未形成完整闭合的圆环，沙丘面积和沙丘高度亦较小。波流作用下的冲刷坑为勺形，在套筒前方和侧前方产生较大冲刷，而筒后冲刷深度较小，沙坑到沙丘由一条沙脊连通，与大直径圆柱在波流作用下的冲刷坑形态类似[26]。波流动床冲刷下的冲刷坑如图5（c）、（d）所示，由于动床冲刷下的桩前床面对冲刷坑存在净输沙，相比波流清水冲刷，局部冲刷深度减小，但整体冲刷范围增大。动床冲刷的床面存在大规模的沙纹，清水冲刷的床面形态则较为平整，沙纹仅出现在桩后。

图5 不同波流条件下的冲刷坑地形图（he=0.25D，Ds=1.5D）

2.2.2 不同套筒高度下的冲刷坑形态对比 图6为Ds=1.5D，U=0.23 m/s，H =0.08 m 时不同高度套筒防护下的冲刷坑地形图。当套筒埋置在初始床面以下，即he＜0 时，如图6（b）所示，筒外冲刷深度和冲刷范围相比无防护时明显减小，此时冲刷过程主要发生在筒内，套筒对桩身的保护效果较差。he＞0 时，冲刷坑形态发生改变，筒外冲刷范围有所减小，筒内冲刷减弱。当he增大到0.5D 以上时，套筒足够将大部分底部来流阻挡在筒外，筒内几乎不发生冲刷，但此时筒外冲刷深度较大，套筒整体的防护效果有限。

图6 不同套筒高度下的冲刷坑地形图（U=0.23 m/s，H=0.08 m，Ds=1.5D）

2.2.3 不同套筒直径下的冲刷坑形态对比 图7给出了套筒高度he= 0.25D，U = 0.23 m/s，H =0.08 m 时不同直径套筒防护下的冲刷坑地形图。如图7（a）所示，当he=0.25D，Ds=1.25D 时，桩与套筒之间的间隙较小，桩筒整体结构与单桩类似，冲刷坑形态与无防护时相比差异不大。套筒直径增大到1.5D 时，主要冲刷过程发生在套筒内，筒外冲刷深度和冲刷范围减小，此时套筒的防护效果较好。随着直径的增大，筒外冲刷范围增大，但套筒筒身逐渐远离桩前下潜水流、马蹄涡等冲刷要素的作用范围，冲刷深度反而减小。

图7 不同套筒直径下的冲刷坑地形图（U=0.23 m/s，H=0.08 m，he=0.25D）

2.3 筒内最大冲深变化分析

图8 分别给出了筒内最大冲刷深度S1随套筒高度he和套筒直径Ds变化的曲线图。图8（a）表示筒内冲刷深度随套筒高度的变化情况，由图可知，当Ds=1.5D，he＜0 时，S1均较大；随着he的增加，筒内冲深减小。图8（b）反映了套筒直径对筒内冲刷的影响。当he=0.25D，Ds从1.25D 增大到1.5D 时，S1逐渐增大；Ds＞1.5D 时，筒内最大冲深随着直径的增大不发生明显的变化。

图8 筒内最大冲刷深度变化情况

图9 为筒内最大冲深S1随he、DS变化的二维等值线图。由图可看出，纯流条件下，he＞0.25D时，筒内原本的冲刷强度较弱，扩大套筒直径使得筒内马蹄涡的强度和活动范围增大，导致冲刷深度增大。波流条件下，波浪不断在套筒内部进行反射和绕射，导致筒内冲刷增强，该情况下扩大套筒直径能够将部分筒内波浪能量释放至筒外，从而减小筒内冲刷深度。

图9 筒内最大冲刷深度二维等值线图

此外，当Ds＞1.5D 时，套筒高度he对筒内冲刷的影响明显比套筒直径Ds的影响更大，这是由于筒内达到平衡状态时的冲刷深度主要是由桩后床面与套筒上边缘的高度差决定的。套筒露出高度比较大时，即使筒内冲刷过程仍在进行，桩前泥沙亦无法被带出套筒，只能堆积在桩后和桩侧，当筒内冲刷坑边坡接近泥沙休止角时，坡上泥沙颗粒便不再移动。桩前马蹄涡的活动范围本身有限，当直径扩大到1.5D 后，筒内冲刷深度不再发生明显变化。

2.4 筒外最大冲深变化分析

图10 为筒外最大冲刷深度S2随he、Ds变化的曲线图。根据图10（a），当Ds= 1.5D 时，S2随he的增加而增大。波流动床条件下，he过大时，筒外冲深甚至会大于无防护下的冲刷深度，这是由于在波流冲刷条件下，除马蹄涡的作用外，筒外泥沙还受到波浪的上扬力，更容易达到起动条件，致使筒外冲刷过程得以增强。波浪在筒前存在反射和绕射等作用，这个作用随着套筒露出高度的增大而增强，这与大直径淹没桩随淹没度变化的规律类似[27]。因此，当套筒初始高度较低时，筒外冲刷过程发展较慢，反之则较快。

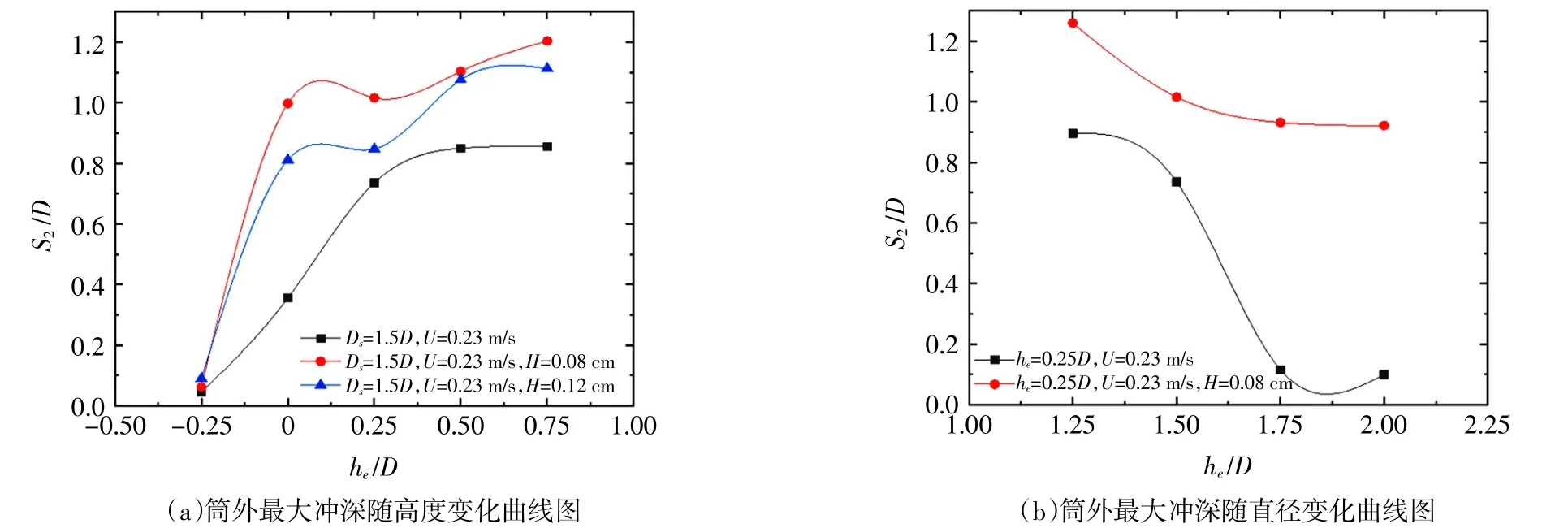
图10 筒外最大冲刷深度变化情况

图11 为S2随he、Ds变化的二维等值线图。结合图10（b）与图11 可知，he＞0 时，纯流冲刷与波流冲刷条件下S2均随Ds增大而减小。当he＜0且逐渐减小，即套筒的埋置深度越来越大时，直径对筒外冲刷的影响越来越小，这与Zhang 等[16]的试验结果相吻合。其原因是，套筒高度较低时，筒前来流大部分未经阻挡直接越过套筒，产生的马蹄涡强度较弱，不足以使筒外泥沙起动，冲刷过程仍主要发生在筒内，此时即使扩大套筒直径，也无法对筒外冲刷造成较大影响。

图11 筒外最大冲刷深度二维等值线图

2.5 最大冲刷深度减小率变化分析

图12 反映了筒内最大冲刷深度减小率R 的变化情况：当套筒直径Ds不变，R 随套筒高度he的增大而增大。he较小时，防护效果较差；he增大到0.25D 以上时，套筒对桩身的防护效果基本满足要求。继续增大高度至0.75D 以上，R 能达到70%以上，但此时筒外冲刷深度较大，与无防护时相比，波流冲刷下的筒外冲深仅减小10%，动床条件下的筒外冲刷甚至比无防护下的桩基冲刷更严重，整体防冲效果较差。

图12 筒内最大冲刷深度减小率变化情况

套筒内、外最大冲刷深度同时影响桩筒结构的整体稳定性，必须综合考虑筒内外的冲刷情况。定义筒内外最大冲刷深度减小率R′（R′=[S0-max（S1，S2）]/S0），以综合考量冲刷防护效果。给出如图13所示的筒内外最大冲刷深度减小率R′的变化曲线，由图可知R′随he、Ds的变化规律：随着he增大，R′先增大后减小；随着Ds增大，R′先增大，后趋于稳定。he= 0.25D，Ds=1.75D 时总体效果最好，此时纯流条件下的R′可达到40%以上，波流条件下也可达25%以上，基本能够满足防护要求。

图13 筒内外最大冲刷深度减小率变化情况

综上所述，采用套筒作为防护措施具有一定可行性，设计布置方案时需合理配置套筒高度和直径，同时考虑套筒内外冲刷深度的影响，以达到最佳的防护效果。

3 结论

本试验对纯流及波流作用下桩筒结构的局部冲刷过程进行了研究，并与无防护下的桩基冲刷进行对比，分析了套筒高度、直径对套筒防护性能的影响，得到如下结论：

（1）在纯流、波流清水冲刷和波流动床冲刷条件下，套筒均能起到一定冲刷防护作用。本试验工况下，筒内最大冲刷深度最高可减小70%，筒内外最大冲刷深度可减小40%左右。he=0.25 D，Ds=1.75D 时套筒总体防护效果最好，此时纯流条件下筒内外最大冲深减小率R′达到40%，波流条件下也可达25%以上，基本能够满足防护要求。

（2）套筒高度he对筒内冲刷的影响较大。直径Ds不变时，筒内最大冲深随套筒高度的增大而减小，但当套筒高度he＞0.75D 时，波流冲刷下的筒外最大冲深与无防护时相比仅减小10%，动床条件下的筒外冲刷甚至比无防护下的桩基冲刷更严重，整体防冲效果较差。

（3）套筒直径Ds主要影响筒外冲刷过程。当he＞0 时，筒外最大冲深随直径增大而减小。当he逐渐减小，直径对筒外冲刷的影响越来越小；波流条件下，he＜0 时，直径仅在1.25～1.5 倍桩径范围内对筒外冲刷产生较大影响，大于1.5 倍桩径时影响甚微。