油状大分子有机物对H型水合物稳定性的影响
张锡彦 ,梁海峰,邵伟强,张 华
(太原理工大学 化学化工学院,山西 太原 030024)
天然气相对于其他化石燃料具有污染排放量少和价格较低的优势[1],因此如何大规模且安全有效地运输天然气成为亟待解决的问题[2]。天然气水合物储运方法具有安全经济、环境友好和储气容量高等优势[3]。I型、Ⅱ型和H型水合物的最大潜能分别为56体积、154体积和201体积[1,4-5]。比较发现,H型水合物在天然气储运方面比I型和Ⅱ型更具发展前景。
天然气水合物的形成需要在高压和低温等特定的热力学条件下进行,使得气体水合物物理和结构特性的测量不准确且成本高,给经济、安全和环境方面带来各种挑战[6]。分子动力学模拟可以在纳米尺度上模拟天然气水合物体系的成核、形成和分解,因此,近年来,该方法被广泛应用于天然气水合物结构以及稳定性的研究[7]。丁丽颖等[8]模拟了不同晶穴占有率和温度对I型甲烷(CH4)水合物晶体稳定性的影响。万丽华等[9-10]研究了客体分子数以及晶穴占有率对I型CH4水合物导热性能和晶体结构稳定性的影响。张庆东等[11]研究了以四氢呋喃(THF)和CH4作为客体分子时,温度和晶穴占有率对Ⅱ型水合物稳定性的影响,得出了添加适量的THF占据大晶穴可以提高水合物稳定性的结论。
H型水合物是RIPMEESTER等[12]于1987年发现的一种与I型和Ⅱ型结构不同的新型气体水合物。梅东海等[13]首次在分子水平上研究了H型水合物结构及其稳定性,提出了H型气体水合物晶体的大、中、小3种晶穴均需被客体分子占据时才能保持稳定。王璐琨等[14]通过分子动力学模拟为H型气体水合物导热系数的模拟计算提供了可靠的势能模型和模拟算法。施军锞等[15]考察了温度对H型水合物晶体结构稳定性的影响,提出了H型水合物稳定性随温度升高而降低并且笼形结构有分解的趋势。周生平等[16]采用分子动力学方法模拟了晶穴占有率和温度变化对H型气体水合物稳定性的影响,表明晶穴填充物对H型水合物稳定性的影响作用高于温度。HAMID等[17]对CH4+大客体分子(新己烷、甲基环己烷(C6H11-CH3)和金刚烷等)二元H型水合物进行了正则系综(NVT)分子动力学模拟,研究了客体分子对H型水合物稳定性的影响,得出CH4+大客体分子的存在有助于提高H型水合物的稳定性。武文志等[1]在恒容条件下,通过实验分析了不同过冷度对环庚烷(C7H14)、环庚酮(C7H12O)、环辛烷和甲基环己烷 4种大客体分子和CH4体系的H型水合物生成过程的影响,发现过冷度越大,水合物生成诱导时间越短,但是以上两篇文献均没有对比不同大客体分子对H型CH4水合物的影响。中子衍射实验从结构角度表明了H型水合物中大晶穴理论上最多容纳的CH4分子数为5个[18]。KUMAZAKI等[19]提出,在温度t= 50 °C,压力p= 1 GPa时,H型水合物大晶穴可容纳2~3个CH4分子并且晶穴结构稳定,但此文献没有提出CH4分子数目变化对H型水合物稳定性的影响。孙志高等[20]利用恒温压力搜索法测量了CH4和C6H11-CH3体系水合物形成的相平衡条件,提出了H型水合物相平衡压力比I型低1.0 MPa以上。
在石油中常含有一些能形成H型水合物的烃类物质,近年来学者已测定了许多大分子烃类水合物的形成条件[20],但是对于大分子烃类水合物的研究多集中在单一促进效果的探讨,目前还鲜有不同大客体分子对H型甲烷水合物影响的报道。本文基于Materials Studio 8.0分子动力学平台考察C7H12O、C6H11-CH3和C7H143种大客体分子对H型气体水合物稳定性的影响,同时研究在大笼中大客体分子数不变时,大笼中CH4分子数对水合物稳定性的影响。
1 模型构建与模拟方法
模拟系统由2 × 2 × 2的H型水合物单晶胞构成,模型包含272个水(H2O)分子,24个512晶穴,16个435663晶穴和8个51268晶穴,将512和435663晶穴加起来研究,即40个小笼、8个大笼。本文研究的C7H12O、C6H11-CH3和C7H143种油状大分子有机物只能占据51268晶穴,CH4由于分子结构比较小既可以占据大晶穴也可以占据小晶穴。C7H12O、C6H11-CH3和C7H143种油状大分子有机物以及H型水合物空笼的结构如图1所示。

图1 大分子有机物和H型水合物空笼结构示意Fig. 1 Macromolecular organics and empty cage structure of structure H hydrate
1.1 模型构建
选用Materials Studio 8.0分子动力学模拟软件进行模型的构建和求解,晶胞中氧原子的初始坐标根据H型水合物晶体衍射试验[12,21-24]确定。其中,水分子构成水合物笼子,氢原子随意放入晶体中并且呈无序排列,满足Bernal-Fowler规则[25]。在x、y、z坐标方向上采用周期性边界条件。
首先采用蒙特卡洛吸附[26]在初始晶胞中的大晶穴分别填充8个C7H14、C6H11-CH3和C7H12O,每个小晶穴填充40个CH4,并将这3种模型命名为A、B、C。其次,占用6个大晶穴用来填充C7H14,小晶穴共填充40个CH4,剩余的两个大晶穴分别放入0、1、2、3和4个CH4分子,并将上述5种模型分别命名为H-0、H-1、H-2、H-3和H-4(例如:H-1即为8个大晶穴中占用其中6个用来填充大客体分子C7H14,而在剩余的两个大晶穴中,分别放入1个CH4分子)。客体分子在模型中的分配如表1所示。

表1 客体分子在模型中的分配Table 1 Distribution of guest molecules in model
1.2 模拟方法
本模拟在恒温恒压系综(NPT)条件下,研究C7H12O、C6H11-CH3和C7H143种大分子有机物对H型水合物稳定性的影响。模拟采用一致性价力场(Consistent valence force field, CVFF)来描述研究体系[27];采用最速下降法和共轭梯度法[26]进行结构优化;采用Ewald加和法描述长程静电作用力[28]和范德瓦尔斯作用力,加和精度为4.18 × 10-4kJ/mol;采用Noose-Hoover热浴法控制模型温度;采用Berendsen方法控制压力;采用简单点电荷(Simple point charge,SPC)势能模型[29]控制水分子之间的相互作用;采用Lennard-Jones势能函数来描述水分子和其他分子间非键相互作用,截断半径为1.2 nm。
本模拟对表1所示的8种模型进行松弛,将模型中的氧原子固定位置,模型温度分别在290 K、300 K、310 K和320 K的条件下进行NVT驰豫,时间步长为1 fs(1 fs = 10-15s),模拟时间为100 ps(1 ps = 10-12s),每5000步输出一帧结构图,然后解除氧原子固定,在相同条件下,采用NPT系综进行动力学模拟,控制压力为3 MPa、8 MPa[20],模拟时间为400 ps,输出步长为5000步。在以上温度压力条件下,研究了环庚酮、甲基环己烷和环庚烷3种油状大分子有机物以及客体甲烷分子数对H型水合物稳定性的影响。
2 结果与讨论
经过对上述8个模型进行NVT驰豫以及NPT分子动力学模拟过程得到晶体最终构型,比较不同温度条件下A、B和C 3种水合物笼型结构的变化,初步判定晶体结构的稳定性,通过计算水合物中主体分子氧原子的径向分布函数、均方位移以及主客体分子的相对浓度( Relative concentration,RC,代表特定法线方向距离r附近,A粒子数密度与系统内该粒子总数密度的比值),来系统地分析温度、压力以及不同客体大分子和CH4分子数对H型水合物晶体稳定性的影响。
2.1 最终构型
在p= 8 MPa,T= 290 K、300 K、310 K和320 K时,A、B和C 3种模型的最终构型分别如图2、图3和图4所示。当T= 290 K时,模型A、B和C都具有清晰的笼形结构,氢键完整并且氧原子具有良好的对称性,表明此时3种模型可以维持稳定的水合物结构。模型A和B的形变程度随着温度的升高而增大,通过对比发现:当T≥ 300 K时,模型A开始分解;当T≥ 310 K时,模型B开始分解。模型C在T= 300 K和310 K时依然可以稳定存在。当T= 320 K时,模型A、B和C都发生了分解,但模型C形变最小,水合物笼形结构坍塌数目最少。

图2 p = 8 MPa时模型A最终构型Fig. 2 Final configuration of model A at p = 8 MPa

图3 p = 8 MPa时模型B最终构型Fig. 3 Final configuration of model B at p = 8 MPa
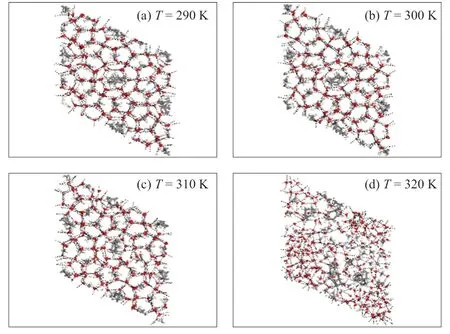
图4 p = 8 MPa时模型C最终构型Fig. 4 Final configuration of model C at p = 8 MPa
通过最终构象可以发现温度越低,水合物晶胞越稳定,并且水合物结构从边缘向内层逐渐分解,其坍塌导致客体分子释放出来,逃逸出来的客体分子会聚集在一起形成团簇。模型C在较高温度下仍可保持稳定,表明此时含C7H14的H型水合物稳定性最好。
2.2 径向分布函数
径向分布函数(Radial distribution function,RDF)表示在距离α粒子质心r(单位:× 10-10m)处出现β粒子的概率,即系统区域密度与平均密度的比值。径向分布函数(gαβ(r))的表达式[7]如式(1)所示:

式中,V为系统体积,×10-30m3;Nα为α粒子的数目;Nβ为β粒子的数目;niβ(r)为以第i个粒子为中心,在r~(r+ Δr)范围内β粒子的数目。
对于水合物来说,当水合物处于稳定状态时,由于氧原子处于初始位置附近,晶格排列有序,并且RDF曲线有多个特征峰,随着r的增大,特征峰逐渐降低;当水合物处于分解状态或不稳定状态时,氧原子处于无序状态,其RDF曲线的第二特征峰及其之后的特征峰将降低直至消失。
模拟时间400 ps,p= 8 MPa,T= 290 K、300 K、310 K和320 K时,A、B和C 3种模型主体水分子中氧原子的径向分布函数如图5所示。通过不同温度下RDF曲线可以得出,当模拟温度不同时,模型C中氧原子的RDF曲线有多个特征峰,模型C水分子中氧原子的RDF曲线在r= 2.775 × 10-10m处出现第一特征峰,表明所有相邻的氧原子都在所获得的距离上,第二和第三特征峰分别出现在r= 4.575 × 10-10m和r= 6.525 × 10-10m处,这与文献[17]一致,验证了模型的准确性。在T= 320 K时模型C中前3个特征峰依然存在,只是第二和第三特征峰相对比于低温时峰高有所下降,峰谷有所升高,表明模型C在T= 320 K时才开始分解,并且分解程度不大;模型A在T= 300 K时,相较于T= 290 K,第二和第三特征峰的峰高明显大幅下降,表明模型A在T= 300 K时水合物笼型部分结构被破坏,水合物晶体逐渐分解;模型B在T= 310 K时,相较于T= 290 K和300 K时第二和第三特征峰的峰高大幅下降,表明模型B在T= 310 K时就开始分解。

图5 不同温度下模型A、B和C水分子中氧原子的径向分布函数Fig. 5 RDF of oxygen atoms in water molecules of A, B and C models at different temperatures
T= 290 K、p= 3 MPa时H-0、H-1、H-2、H-3和H-4 5种模型水分子中氧原子的径向分布函数如图6所示。由图6可知,H-3和H-4的RDF曲线有多个明显的特征峰并且峰高最高,峰谷最低。

图6 T = 290 K、 p = 3 MPa时模型H-0、H-1、H-2、H-3和H-4水分子中氧原子径向分布函数Fig. 6 RDF of oxygen atoms in water molecules of H-0, H-1,H-2, H-3 and H-4 models at T = 290 K and p = 3 MPa
在恒定压力的同一模型下,随着温度的升高,水分子中氧原子的RDF曲线的峰高降低,但是峰谷升高,由于氧原子的有序度小,这种行为表现为水分子和水合物笼中氧原子的低稳定性,因此,当压力恒定,温度升高时,水合物分解的可能性将增加。
2.3 均方位移
在分子动力学运动过程中,模型中粒子时刻不停移动,使得每个瞬间各个粒子的位置都不一样。粒子位移平方的平均值称为均方位移(Mean squared displacement,MSD,单位:× 10-20m2)[30],其表达式如式(2)所示:

式中,N为模型中的粒子总数;Ri(t)为粒子i在时间为t时的位置;Ri(0)为粒子i在时间为0时的位置。
MSD反映了某一时刻模型中分子的空间位置与初始位置的偏离程度。由于分子不能在晶体(固体)中自由移动,所以稳定的水合物晶体中氧原子的均方位移值接近一个恒定值,即MSD的斜率接近于0。而当水合物处于分解或失稳状态时,由于分子的随机运动,MSD的大小随模拟时间线性增加,说明氧原子偏离初始位置,此时氧原子的位置坐标相对自由,水合物处于分解或失稳状态。
模拟时间400 ps,p= 8 MPa,T= 290 K、300 K、310 K和320 K时,A、B和C 3种模型主体水分子中氧原子的MSD如图7所示。

图7 不同温度下模型A、B和C水分子中氧原子的均方位移Fig. 7 MSD of oxygen atoms in water molecules of A, B and C models at different temperatures
由图7可知,当T不同时,A、B和C 3种模型中氧原子的均方位移都是模型C最小,并且在T≤ 310K时模型C的MSD接近一个恒定值。此时,水合物在初始位置上转动或振动,偏离位置较小。由于分子不能在晶体(固体)中自由移动,可推测在温度T≤ 310 K时模型C中水合物的笼形结构完整,此时模型C是一个稳定的水合物晶体。由于分子的随机运动,MSD的大小随模拟时间线性增加,说明氧原子偏离初始位置,此时氧原子的位置坐标相对自由,水合物处于分解或失稳状态。根据MSD的线性变化可以得出模型A从T= 300 K开始分解,模型B从T= 310 K开始分解,模型C从T= 320 K才开始分解。
T= 290 K、p= 3 MPa时H-0、H-1、H-2、H-3和H-4 5种模型水分子中氧原子的均方位移如图8所示。由图8可知,H-3和H-4的MSD值较小并且斜率接近为零。
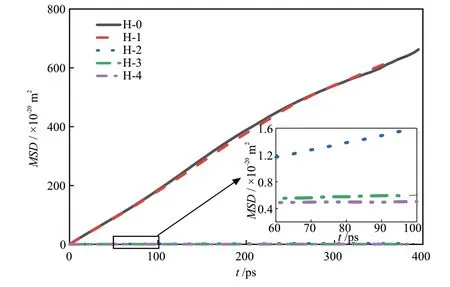
图8 T = 290 K、p = 3 MPa时模型H-0、H-1、H-2、H-3和H-4水分子中氧原子的均方位移Fig. 8 MSD of oxygen atoms in water molecules of H-0, H-1,H-2, H-3 and H-4 models at T = 290 K and p = 3 MPa
通过对比不同温度下同一模型的MSD,发现随着温度升高,MSD值增大,表明低温有利于水合物晶体稳定;通过对比同一温度下不同油状大分子有机物的MSD得出以C7H14(模型C)作为大客体分子的H型水合物稳定性最好;通过控制温度和压力,减小大客体分子数,在剩余的大笼中分别填充0、1、2、3和4个CH4分子,发现水合物的稳定性随之升高。
2.4 相对浓度
相对浓度曲线可以用于分析系统内各粒子的密度分布信息。

式中,ρr为在r处A粒子的相对浓度;ρi为r处附近区域的A粒子数密度,个/ × 10-30m3;ρtotal为A粒子在盒子内的总数密度,个/ × 10-30m3。
通过前文分析得出C7H14为大客体分子时H型水合物稳定性最好,条件最温和,所以进一步采用模型C来分析H型水合物晶体在稳定和分解时模型内主客体分子相对浓度的变化。
T= 290 K、p= 3 MPa(稳定时)和T= 320 K、p= 3 MPa(分解时)模型内主体水分子和大客体分子C7H14以及小客体分子CH4的相对浓度随x轴的变化趋势如图9所示,其中纵轴代表分子的相对浓度,横轴代表水合物盒子(1,0,0)方向的位置坐标。由图9(a)可知,水分子在T= 290 K时呈周期性对称分布,这与初始建立的2 × 2 × 2周期性模型相对应。稳定时,水分子沿着x轴呈两个峰高和一个峰谷周期性分布,但当水合物分解时,只有r= 15 × 10-10m附近的峰高存在,外层的峰消失,说明水合物笼形结构从外层开始分解。由图9(b)和9(c)可知,稳定时,C7H14和CH4分子沿着x轴对称分布,有明显的峰值。当T= 320 K时,水合物笼形结构外层开始坍塌,大笼内的C7H14和CH4分子逃逸,在水合物模型内自由移动,导致相对浓度曲线峰高降低、峰谷升高,相对浓度曲线对称性与周期性分布消失。
在水合物晶体处于稳定状态时,模型内H2O、C7H14以及CH4分子沿着(1,0,0)方向呈规则周期性分布。在水合物晶体处于失稳状态时,晶穴内部的C7H14和CH4分子逃逸并在水合物模型内自由移动,导致相对浓度曲线对称性与周期性分布消失。
3 结论
在NPT系综下,采用分子动力学模拟方法研究了C7H12O、C6H11-CH3和C7H143种油状大分子有机物作为大客体分子对H型水合物稳定性的影响,并在相同温度压力条件下,保持大客体分子数不变时,研究了客体CH4分子数对H型气体水合物稳定性的影响,得到以下主要结论。
(1)C7H12O、C6H11-CH3和C7H14作为客体分子可以占据H型CH4水合物大晶穴,并且油状大分子有机物的存在有助于提高H型CH4水合物的稳定性。
(2)H型水合物的稳定性随模拟温度的升高而降低,不同油状大分子有机物作用下,水合物稳定性顺序依次为C7H14> C6H11-CH3> C7H12O。
(3)水合物笼形结构是由边缘向中心逐层分解的。水合物笼形结构坍塌而释放出来的客体分子会聚集形成团簇。
(4)当大笼中大客体分子数不变时,水合物的稳定性随着大笼中CH4分子数的增加而升高,大笼中最多可以稳定存在4个CH4分子,且每个大笼中存在4个CH4分子的H型水合物稳定性最高。

