激光跟踪仪与机器人坐标转换公共点的选取方法

徐福乾，范百兴，黄 赫，段童虎，李慧敏，孙晨磊

(1.信息工程大学，郑州 450001；2.郑州信大先进技术研究院，郑州 450001)

近年来，工业机器人作为现代制造业的核心装备，凭借其稳定性强、可靠性高等特点，成为推动制造业发展的核心力量，机器人技术的发展与应用对国民经济建设和国防建设具有重要意义[1]。工业机器人重复定位精度很高，但绝对定位精度较差，未经标定前的绝对定位精度通常为±2～3 mm，难以满足精密零部件加工、航天器装配、武器装备生产等高端产业需求[2]。对工业机器人的运动学参数进行标定是提高其绝对定位精度的主流方法[3-6]。机器人运动学参数标定可分4个阶段：建模、测量、参数辨识、误差补偿[7]。在机器人末端位姿误差测量阶段，常用激光跟踪仪获取机器人的末端位姿误差[8-9]。进行误差测量前，必须解决激光跟踪仪测量坐标系与工业机器人基坐标系的统一问题。如何快速、准确获取坐标系转换参数是工业机器人应用领域的热点问题之一。

针对激光跟踪仪测量坐标系与工业机器人基坐标系的统一问题，张博等[10]采用机器人单轴运动与示教器读数相结合的方法，利用机器人运动轨迹的几何关系求解转换参数，但该方法操作复杂，需要采集大量数据才可保证解算精度，全过程所需时间较长。向民志等[11]利用基于距离约束的方法标定出工具坐标系，再通过基于罗德里格矩阵的最小二乘迭代法进行坐标转换参数求解，该方法能够显著提高转换参数求解的效率和质量。冯晓波等[12]利用基于奇异值分解的最小二乘拟合算法对转换参数进行求解。上述方法，均没有阐述公共点的空间几何分布及选点问题，在公共点空间几何分布较密集时，容易出现解算参数不稳定、不可靠等情况。为此，文中提出了一种基于象限分布的公共点选取方法，该方法在原有的基于距离约束的工具中心点标定的基础上，顾及了公共点空间几何分布对转换参数求解精度的影响。该方法只需在机器人工作空间内的示教点位中选取6个空间几何分布合理的公共点，即可快速、准确的求解坐标转换参数，具有稳定性强、精度高、效率高等特点，适合在工业机器人工作现场直接使用。

1 坐标系转换方法

1.1 坐标系转换系统

坐标系转换系统中涉及到的硬件主要有激光跟踪仪及其配套测量设备、工业机器人、辅助工装等，如图1所示。此外，还涉及到多个空间直角坐标系，定义在激光跟踪仪上的坐标系为激光跟踪仪测量坐标系，用{M}表示；定义在工业机器人安装基座上的坐标系为机器人基坐标系，用{B}表示，该坐标系在机器人运动过程中始终保持稳定；定义在工业机器人法兰末端上坐标系为法兰末端坐标系，用{E}表示，该坐标系是工具坐标系的参考基准；定义在机器人法兰末端安装的工具上的坐标系为工具坐标系，用{T}表示，该坐标系的原点为工具中心点(Tool Centre Position，TCP)，TCP相对法兰末端坐标系{E}固定不动，机器人以TCP作为参考点进行运动轨迹规划。文中定义靶球中心P为工具中心点，靶球通过移动靶球基座与工业机器人法兰末端实现固连。

图1 测试系统模型

实验过程中，激光跟踪仪与工业机器人基座的相对位置关系始终保持稳定。控制机器人携带靶球在其工作空间内示教若干个不同点位，同时记录在各点位处的示教器读数及激光跟踪仪测量读数。

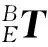
(1)

(2)

即

进一步展开得：

(4)

首先，利用基于距离约束的TCP标定方法，获取TCP(靶球中心P)在法兰末端坐标系{E}中的位置。然后，根据式(4)计算出TCP在机器人基坐标系{B}中的位置[15]。其次，考虑到公共点点位的空间几何分布对转换参数求解精度的影响，采用文中基于象限分布的公共点选取方法选取公共点，求取转换参数。最后，利用未参与坐标转换参数计算的其余示教点位进行坐标转换，检验坐标转换结果的质量。

1.2 TCP标定方法

由1.1所述可知，在进行坐标转换之前，需要对TCP进行标定。实验过程中，TCP相对于法兰末端坐标系{E}稳定不动，TCP标定即获取靶球中心P在法兰末端坐标系{E}中的位置。

根据坐标变换原理，靶球中心P在机器人基坐标系{B}中的坐标可表示为：

(5)

(6)

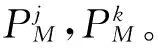
(7)

众所周知，空间中任意两点，它们在同尺度的不同坐标系中坐标值可能不同，但两点之间的距离在同尺度的不同坐标系中是相同的。因此，在j,k位置时，靶球中心P之间距离在机器人基坐标系{B}和激光跟踪仪测量坐标系{M}中是相同的。即：

(8)

将式(5)代入上式可得：

(9)

(10)

进一步展开得非线性方程：

(11)

对式(11)通过一阶泰勒级数展开，进行线性化处理，整理得到误差方程形式为：

(12)

其中，

2 公共点选取

2.1 公共点对转换参数解算的影响分析

坐标系转换参数的求解精度与公共点选取密切相关，影响转换参数求解精度的主要因素有公共点的精度、数量以及空间分布。

坐标转换的精度主要取决于参与计算坐标转换参数的公共点的测量精度，即由机器人示教器和激光跟踪仪分别获取的工业机器人每次运动停定后靶球中心P的三维坐标的精度。实验所用激光跟踪仪型号为Leica AT901-B，三维点坐标标称测量精度为±(15 μm+6 μm/m)，采用直径38.1 mm的RRR1.5"精密靶球作为反射棱镜，配合该靶球在10 m工作范围内，点位精度优于±75 μm。所用机器人为ABB IRB-4600型工业机器人，有效载荷40 kg，重复定位精度标称为±0.06 mm，出厂前经过严格标定，其绝对定位精度在±1 mm左右。实验过程中，激光跟踪仪放置在工业机器人工作空间之外约1.5 m处，如图2所示。激光跟踪仪测量的点位精度优于±75 μm，该精度远高于工业机器人绝对定位精度。因此，坐标转换结果的好坏主要取决于工业机器人的绝对定位精度。

图2 实验系统

公共点数量也是影响坐标系转换参数的因素之一。两个空间直角坐标系转换参数的解算，至少需要3个公共点。公共点数量过少时，公共点的点位误差对转换结果影响程度加深，容易造成解算结果不可靠。公共点数量一般为3～6个，不宜超过6个，因为公共点数量过多时，会额外增加计算的工作量，且对转换参数的求解精度提高不明显[16]。

在工程实际中，公共点的点位空间分布情况比较复杂，可能遇到公共点点位空间分布较为密集，公共点与转换点距离较远等情况[17]。一般地，坐标系转换参数解算精度与参与计算的公共点的空间分布几何强度呈正相关。公共点的点位精度和数量相同时，公共点空间分布较密集时，容易导致转换参数解算过程中法方程的病态性。公共点分布越离散，空间几何强度越好，求解精度越高，反之求解精度越低[18]。

2.2 基于象限分布的公共点选取方法

基于象限分布的公共点选取方法是沿着机器人基坐标系的X轴、Y轴，将机器人工作空间分为4个象限，如图3所示。工业机器人安装在自动导引运输车(Automated Guided Vehicle，AGV)承载面上，AGV可携带工业机器人在空间内实现位移。实验过程中，AGV展开4条液压支腿，增大平台与地面摩擦力，保证平台的稳定性满足实验要求。

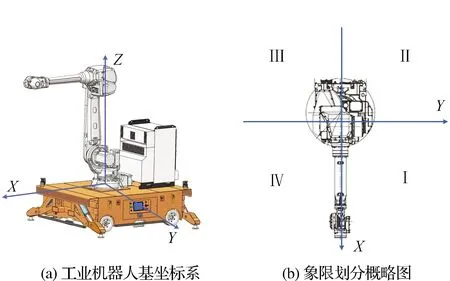
图3 基坐标系象限划分

基于象限分布的公共点选取方法主要顾及公共点的空间几何分布对转换结果的影响。根据公共点在工业机器人实际工作空间内不同象限中的分布情况，选取出分布较为离散的一组公共点参与坐标转换参数计算，以提高转换参数的求解精度。由2.1可知，为提高坐标转换参数的求解精度，同时顾及操作和数据处理的难易程度，选取6个公共点作为解算起始数据。本次实验中所用机器人的控制器对其作业空间存在一定程度运动限制，控制工业机器人在其作业空间的安全区域内示教22个位置(若无运动限制，可对称均匀示教24个位置)，如图4所示。从其中选取若干点作为解算坐标转换参数的公共点，其余未参与转换参数计算的点作为转换点来检核坐标转换的精度。基于象限分布的公共点选取方法有以下几个步骤：

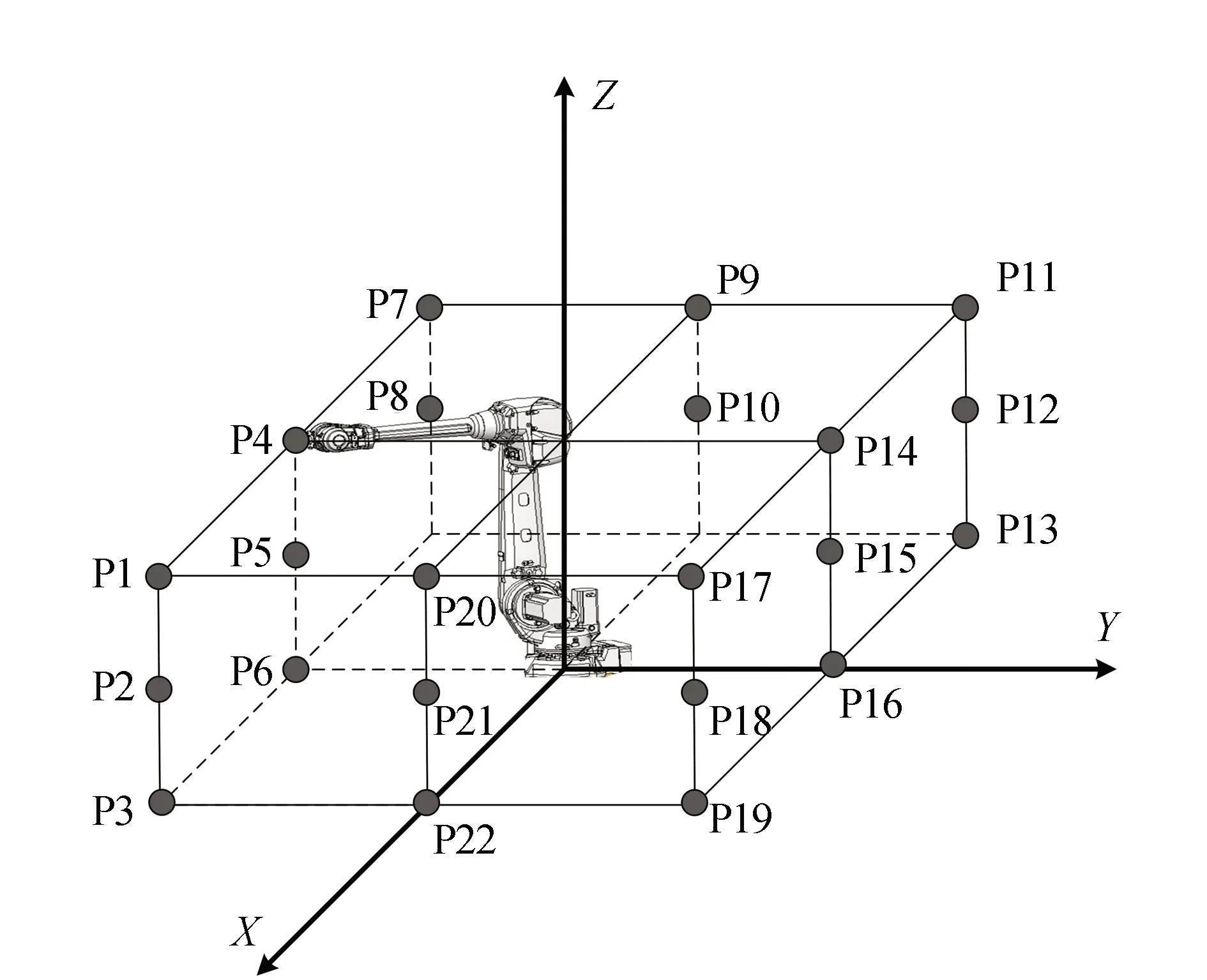
图4 示教点位分布图

1)对全部示教点位进行重心化。由于激光跟踪仪测量精度明显高于机器人的绝对定位精度，故选取激光跟踪仪测得的示教点坐标进行重心化。即求得全部示教点在激光跟踪仪测量坐标系下的X,Y,Z坐标分量上的平均值，记重心点为G0。

2)求各示教点至重心点G0的距离。计算各个示教点至经过重心化后获得的重心点G0之间的距离。

3)在象限Ⅰ、Ⅱ、Ⅲ、Ⅳ中分别选取1个距离重心点G0最远的点作为公共点。选择公共点时要令相邻象限中的公共点在Z轴上高度不同。记象限Ⅰ、Ⅱ、Ⅲ、Ⅳ中选取的公共点依次为1、2、3、4号公共点。

4)将象限Ⅰ、Ⅱ中选择的两个公共点的坐标取平均，记为G1。在剩余示教点中选择一个距离G1点最近的点，记为5号公共点。

5)将象限Ⅲ、Ⅳ中选择的两个公共点的坐标取平均，记为G2。在剩余示教点中选择一个距离G2点最近的点，记为6号公共点。

利用上述基于象限分布的公共点选取方法，选取出的公共点为P3，P5，P7，P13，P15，P17，记该组公共点为象限分布组合。另随机选择两组与上述公共点空间分布不同的示教点作为公共点随机组合一(P3，P5，P7，P9，P10，P19)、随机组合二(P1，P13，P15，P17，P20，P21)，进行对比实验。利用各公共点组合求解出转换参数后，为表示其精度，利用未参与转换参数计算的其余示教点(P2，P4，P6，P8，P11，P12，P14，P16，P18，P22)作为转换点进行坐标转换，检验转换结果的精度。

3 实验与结果分析

坐标转换的实质即获取激光跟踪仪测量坐标系与机器人基坐标系之间的相对位姿关系。实验过程中，应确保激光跟踪仪与机器人基座的相对位姿保持稳定。实验前，已使用激光跟踪仪对工业机器人不同运行状态下的AGV平台的稳定性进行了测试，其稳定性满足坐标转换实验要求。实验过程中，首先，通过TCP标定原理，计算出靶球中心P在机器人法兰末端坐标系{E}中的位置；然后，通过3组公共点进行坐标系转换，采用最小二乘法求解转换参数；最后，用未参与转换参数计算的示教点位进行转换，分析转换结果的精度。

3.1 TCP标定

TCP标定的目的是获取靶球中心在工业机器人法兰末端坐标系{E}中的位置。由1.2可知，求解TCP的位置，至少需要测量机器人工作空间内的3个示教点。为进一步提升TCP求解精度以及转换参数的求解效率，使用解算转换参数的公共点作为TCP解算的数据，并利用1.2所述TCP标定方法解算TCP的位置。3组公共点的激光跟踪仪测量坐标及对应的机器人示教器读数分别如表1、表2、表3所示，各表中A，B，C分别表示法兰末端坐标系绕机器人基坐标系Z轴、Y轴和X轴的旋转角度。

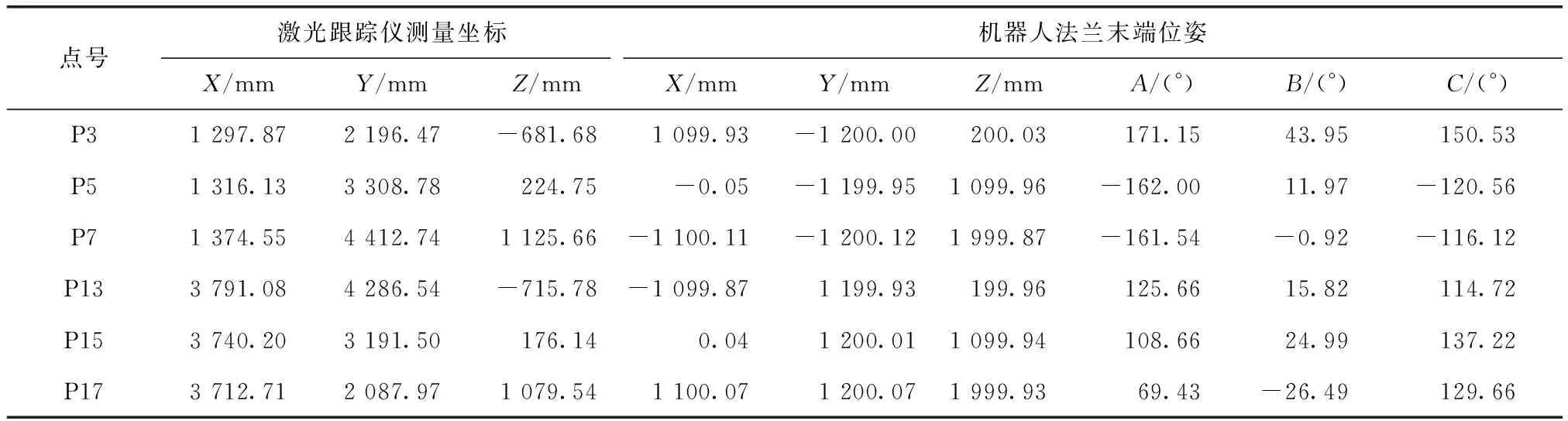
表1 象限分布组合中各点激光跟踪仪测量坐标及示教器读数

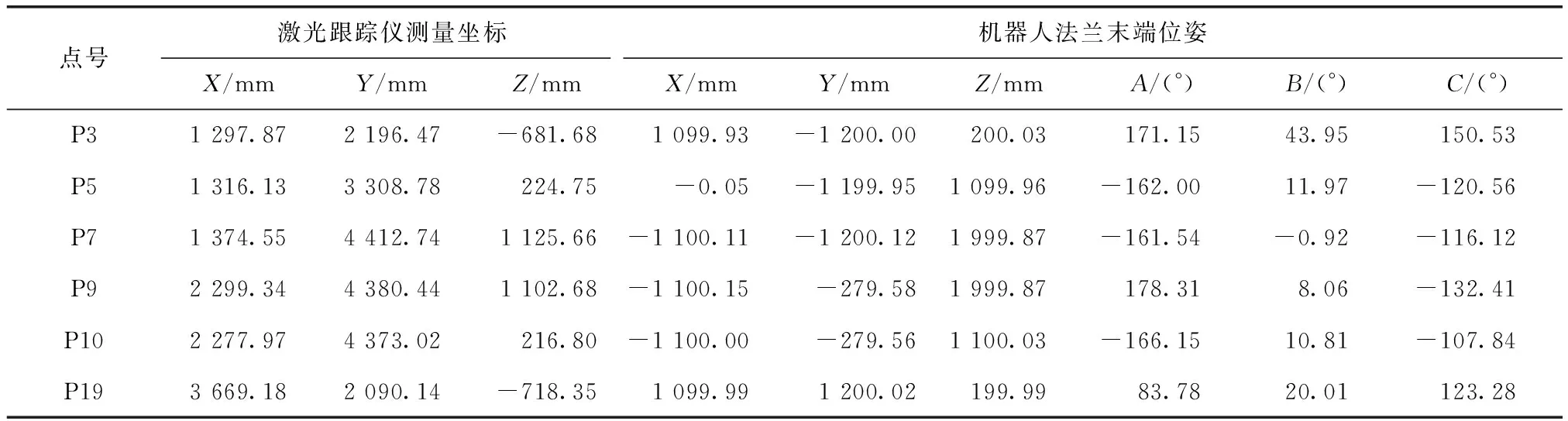
表2 随机组合一中各点激光跟踪仪测量坐标及示教器读数

表3 随机组合二中各点激光跟踪仪测量坐标及示教器读数

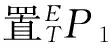
3.2 坐标系转换实验

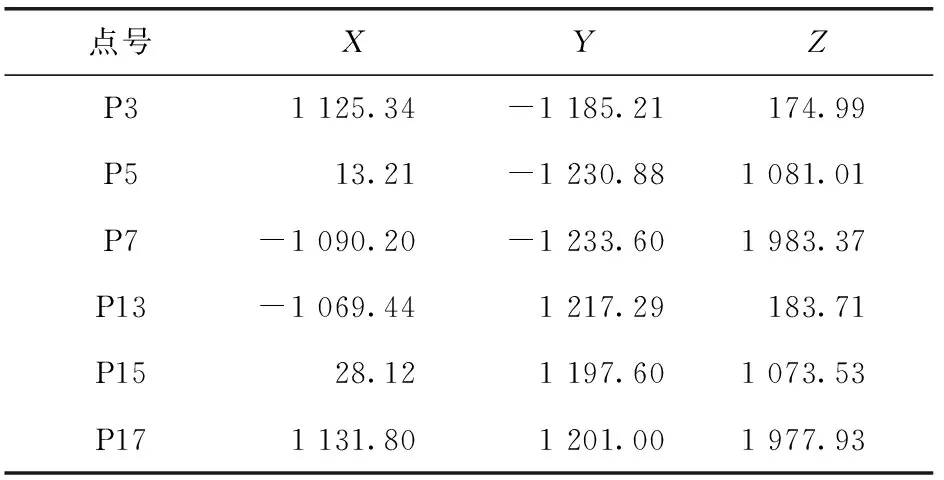
表4 象限分布组合中各点在基坐标系中坐标 mm

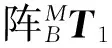
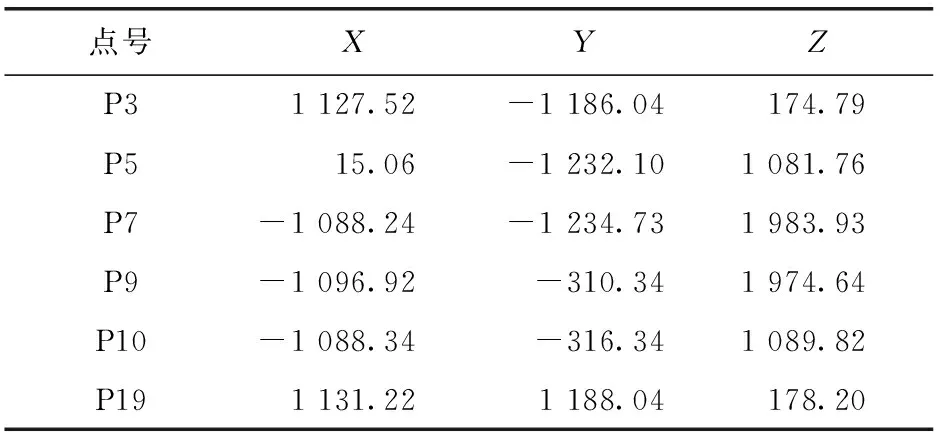
表5 随机组合一中各点在基坐标系中坐标 mm

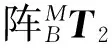
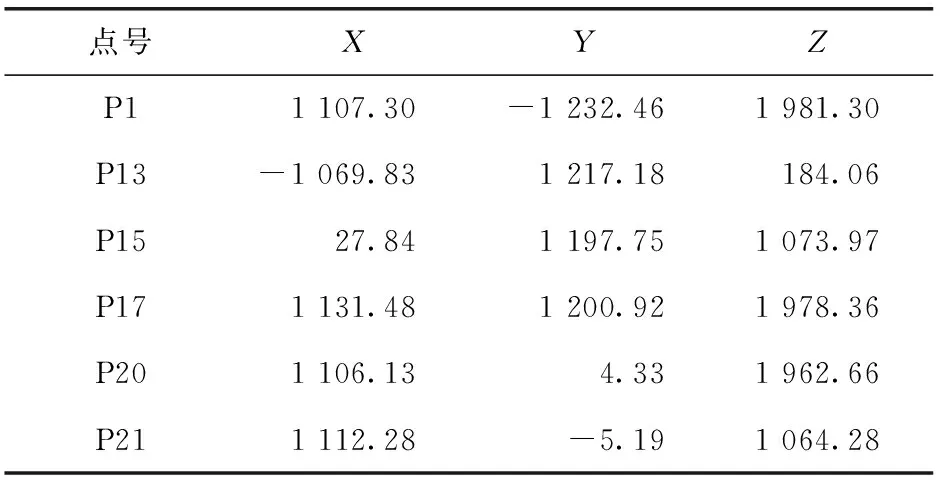
表6 随机组合二中各点基坐标系中坐标 mm

3.3 转换精度分析

将转换点转换后的点位误差和X,Y,Z方向上的转换较差绝对值的平均值作为指标来衡量基于象限分布的公共点选取方法的可行性。

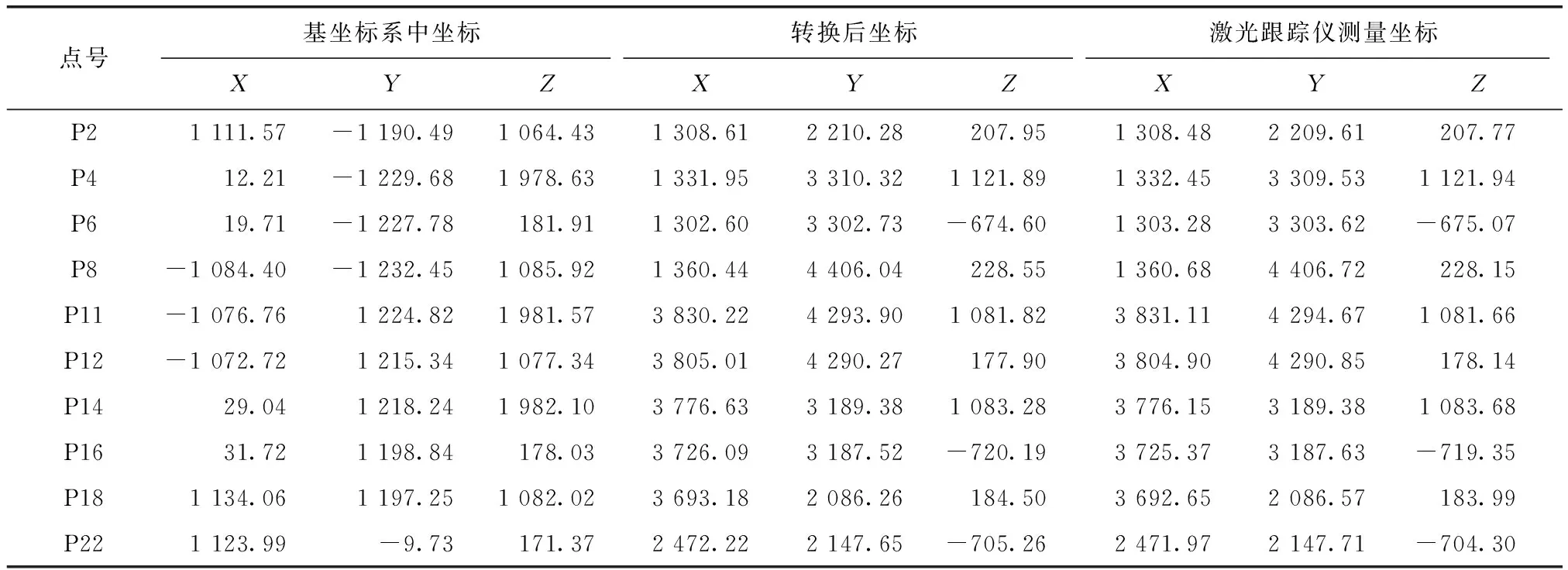
表7 公共点象限分布组合对应实验中转换点坐标 mm

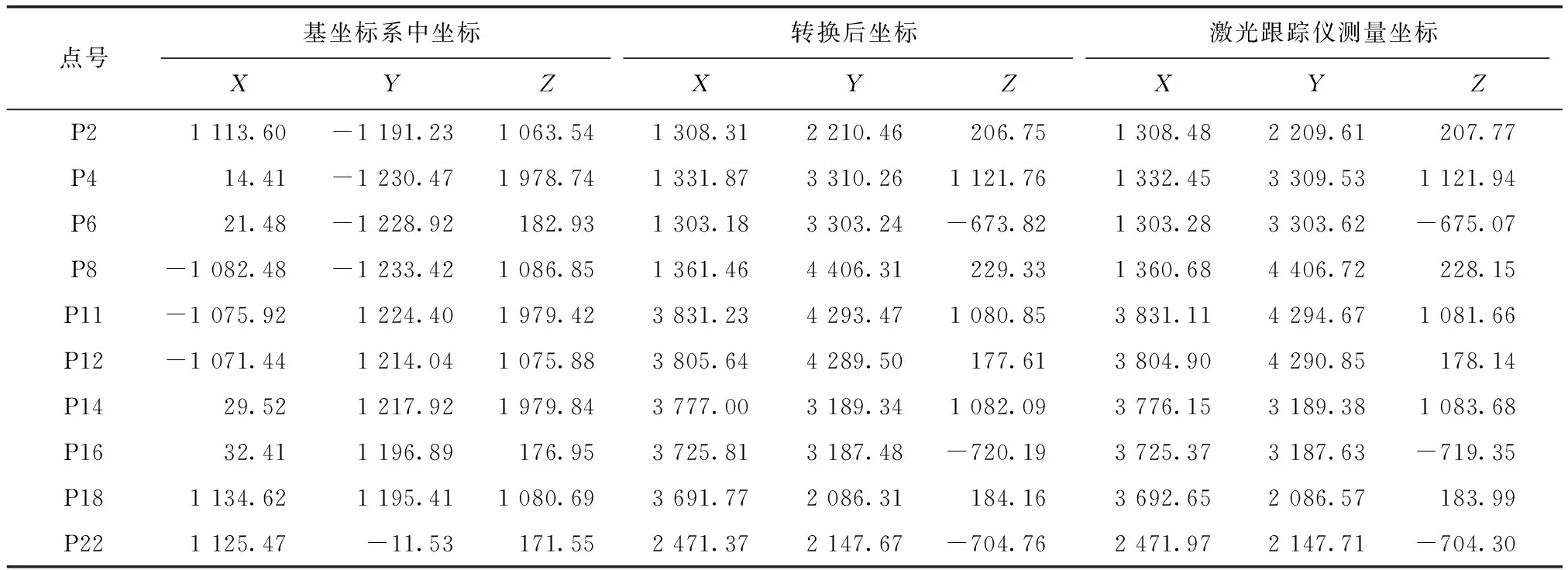
表8 公共点随机组合一对应实验中转换点坐标 mm

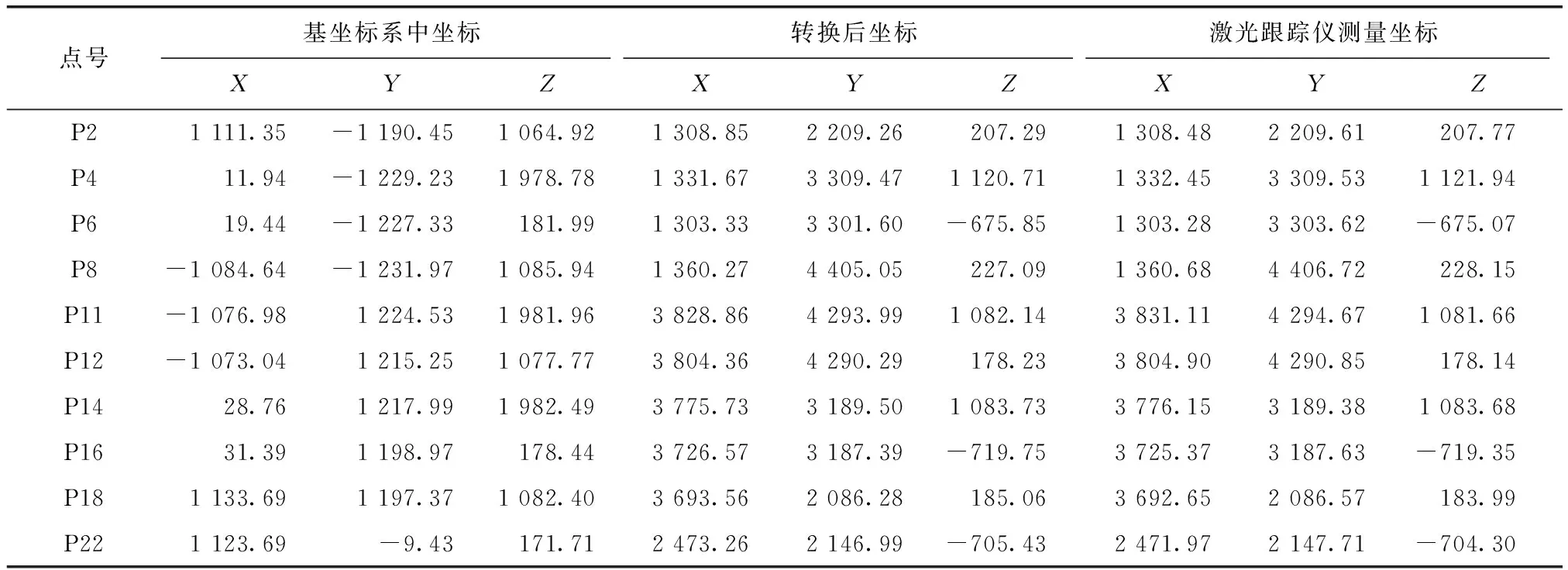
表9 公共点随机组合二对应实验中转换点坐标 mm

将经过坐标转换后得到的转换点在激光跟踪仪测量坐标系下的坐标与激光跟踪仪直接测得的转换点的坐标作差，分别得到3组公共点组合对应实验的转换点较差。3组公共点组合对应实验中各转换点在X，Y，Z方向上的较差及各方向上较差绝对值的平均值如表10所示，点位较差分布如图5所示。

表10 各公共点组合实验转换点较差 mm

图5 转换点较差分布图(mm)

进一步统计3组公共点组合实验的转换点X，Y和Z坐标分量的转换精度以及坐标转换的点位精度，得到的统计结果如表11所示。

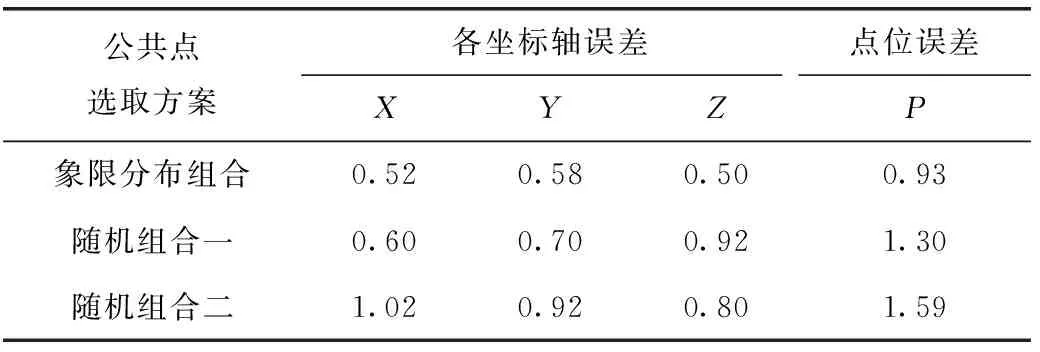
表11 坐标转换精度统计 mm

由表10、表11可知，公共点象限分布组合对应实验中转换点上转换较差绝对值的平均值分别为0.45 mm、0.49 mm、0.42 mm，相对于随机组合一对应实验中转换点X，Y和Z方向上转换较差绝对值的平均值0.53 mm、0.54 mm、0.80 mm和随机组合二对应实验中转换点X，Y和Z方向上转换较差绝对值的平均值0.82 mm、0.67 mm、0.68 mm的转换精度更好，且在X，Y和Z3个方向上的数值更加均衡。由图5也可看出，公共点象限分布组合的转换点较差分布相对于随机组合一和随机组合二更加集中，即坐标转换的稳定性更强。

公共点象限分布组合对应实验中各转换点在X，Y和Z坐标分量上RMS误差分别为0.52 mm、0.58 mm、0.50 mm，综合RMS误差为0.93 mm。公共点随机组合一对应实验中各转换点在X，Y和Z坐标分量上RMS误差分别为0.60 mm、0.70 mm、0.92 mm，综合RMS误差为1.30 mm。公共点随机组合二对应实验中各转换点X，Y和Z坐标分量上RMS误差分别为1.02 mm、0.92 mm、0.80 mm，综合RMS误差为1.59 mm。随机组合一对应实验中转换点综合RMS误差约为象限分布组合对应实验结果的1.4倍，随机组合二对应实验中转换点综合RMS误差约为象限分布组合对应实验结果的1.7倍。公共点象限分布组合对应实验中各转换点在各坐标分量上的误差和点位误差均比随机组合一和随机组合二对应实验的转换误差小，亦说明其转换质量较好。

综上所述，公共点象限分布组合对应实验的转换结果的质量优于随机组合一和随机组合二的转换结果的质量，公共点象限分布组合求解的坐标转换参数的精度更高，其稳定性也更强。

4 结束语

文中提出了一种激光跟踪仪与机器人基坐标系转换参数求解过程中所需公共点的选取方法。该方法顾及公共点空间几何分布对转换参数求解精度的影响，在公共点精度一定的情况下，仅需6个空间几何分布较合理的公共点，即可快速求解出激光跟踪仪坐标系与机器人基坐标系的转换参数。实验表明，采用基于象限分布的公共点选取方法所选取的公共点，解算出的转换参数的精度优于随机公共点组合求解出的转换参数的精度，且稳定性更强，在实际工程应用中具有良好的有效性和可行性，适合一般工业现场使用。