煤矿抽水蓄能电站水下巡检机器人姿态调节系统建模与分析

何 涛，王传礼，高 博，陈 凡，赵凯平，王伟俊

（1.安徽理工大学 机械工程学院，安徽 淮南 232001；2.深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；3.矿山智能装备与技术安徽省重点实验室，安徽 淮南 232001；4.安徽矿山机电装备协同创新中心，安徽 淮南 232001；5.国网安徽省电力有限公司 电力科学院，安徽 合肥 230061）

0 引 言

煤炭是我国主体能源，经过长期大规模的开采，许多煤矿煤炭资源趋于枯竭，或已经枯竭关闭，或因政策性关闭，从而形成待转型煤矿［1］。 中国工程院预测2020 年我国关闭矿井数量将达到1.2 万处，2030 年将到达1.5 万处［2－3］。 关闭矿井中赋存大量可利用资源，直接关闭或废弃不仅会造成资源的巨大浪费，还可能引发安全事故、环境污染及系列社会问题［4］。 为此谢和平等［5－6］、袁亮等［4］提出在我国煤矿井下开展抽水蓄能电站建设，为关停矿井的资源化利用、立体式开发和全面转型升级提供了新思路。 李庭等［7］、罗魁等［8］等针对利用废弃矿洞建设抽水蓄能电站的技术可行性开展了大量论证，论证结果均表明其在理论和技术层面是可行的［9－10］。 但废弃矿洞地下空间稳定性差，人工勘察风险大；电站建成后，其水下洞室和尾水系统错综复杂，人工巡检难度大且安全性难以得到保证，亟需专门的水陆两栖机器人。

水陆两栖机器人作为可移动的载体，其沉浮及姿态调节对机器人的综合移动性能影响巨大［11－12］。目前国内外水下机器人姿态控制主要有2 种形式，即推进器控制和重浮心变化控制［13－14］。 邱中梁等［15］设计了水银液压纵倾调节系统，该系统调节效率高、能耗较低，但液态水银密封难，且有剧毒，其泄漏易造成水体严重污染。 贾连超等［16］提出了用于水下机器人姿态调节的电磁式水下合成射流激励器，该系统能实时调节平均推力和推进效率，但其对于姿态调节过程中姿态倾角的控制难以做到实时精准，且可能会激起波纹干扰水下机器人作业。 高世阳等［17］提出了一种深海油馕式浮力调节系统，其具有良好的可行性和实用性，但其在深海压力以及复杂的海底环境下易造成油液泄漏。 同样“潜龙一号”作为深6 000 m 级自主水下航行器，其浮力调节系统采用液压油作为工作介质，但为了减少浮力调节时的能量损耗，其采用了单向浮力调节系统［18］。由于油馕式浮力调节系统结构复杂、密封易失效以及皮囊易老化及泄漏污染等问题，我国的深7 000 m级载人潜水器“蛟龙号”采用了海水浮力调节系统，而其纵倾调节因其自身重量较大，仍然采用了水银调节方式［19］。

由此可知，现有液压姿态调节系统多采用油压调节或者水银调节方式，二者均易造成泄漏和污染，且机构复杂；且大多数水下移动机器人的沉浮调节和姿态调节系统相互独立，增加了设计成本和系统的复杂性。 为此，设计了一种兼具沉浮和姿态调节功能的一体化的姿态调节系统，且考虑到煤矿抽水蓄能电站水下巡检机器人的环保要求，整个系统采用全水液压驱动，并在此基础上建立机器人的三维模型，进而开展姿态调节系统的建模与仿真分析。

1 巡检机器人姿态调节系统

1.1 姿态调节系统结构及原理

履带行走机构具有较强的复杂地形通过能力［20］，为此机器人在陆地采用履带行走，而在水下洞室和尾水系统内通行采用推进器推动。 煤矿抽水蓄能电站水下巡检机器人三维模型如图1 所示。 机器人的全水液压沉浮－姿态调节一体化系统如图2所示。 该系统主要由分设于左压载舱和右压载舱内部的姿态活塞缸、变量泵及控制阀等组成。 两姿态活塞缸结构完全相同且关于机体对称布置，姿态活塞缸主要由前腔、后腔、前腔活塞、后腔活塞、弹簧腔Ⅰ、弹簧腔Ⅱ和中间活塞等组成。

图1 巡检机器人三维模型Fig.1 3D model of underwater inspection robot

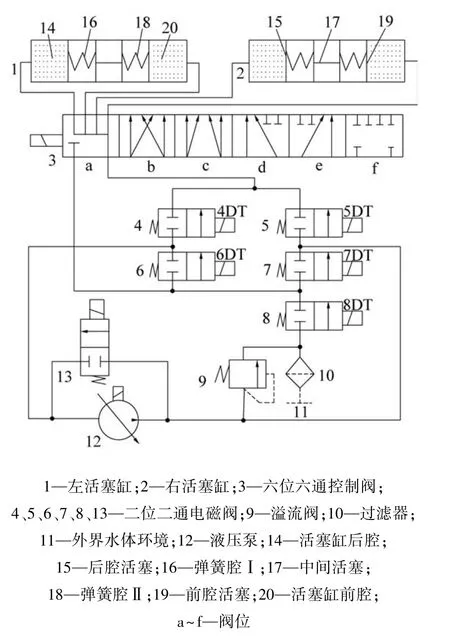
图2 姿态调节系统原理Fig.2 Schematic of attitude regulation system

姿态调节液压系统采用水液压驱动方案，传动介质来自机器人外部水体环境，为改善液压系统的防腐问题，液压元件均采用防腐耐磨材料加工。 机器人的姿态调节包括沉浮、纵倾（包括前倾和后倾）、横倾（包括左倾和右倾）、对角侧倾（包括右前倾、右后倾、左前倾和左后倾）4 种调节状态。 其中沉浮调节主要通过液压泵迫使左右活塞缸内的水介质与外界水体进行质量传送来实现，当外界水体被泵入左右活塞缸则机器人下沉，当左右活塞缸内的水介质被抽入外界水体时，则机器人上浮；后3 种状态为姿态调节状态，一般姿态调节时要确保机器人处于悬停状态，并关闭电磁换向阀8，此时系统与外环境水体环境隔绝，可确保姿态调节过程中机器人总重量恒定（即悬停状态）。

不同状态下电磁阀的电磁铁动作见表1。 对角侧倾状态，由表1 中纵倾和横倾复合控制得到。 其中右前或右后侧倾状态，可在右侧倾状态下，将六位六通控制阀调至d 阀位，控制液体介质仅在右活塞缸前后腔之间传输。 同理，对于左前或左后侧倾状态，可在左侧倾状态下，将六位六通专用阀调至e 阀位，使液体介质仅在左活塞缸前后腔之间交换。 六位六通控制阀的f 阀位为闭锁阀位，控制左右姿态活塞缸均处于紧闭状态。 上述姿态调节方案大幅简化了控制流程，提高了调节效率，且可确保姿态调节过程中，机器人本体始终处于悬停状态，提高了机器人调姿过程的稳定性。

表1 控制阀动作顺序Table 1 Control valve operation sequence

1.2 系统设计参数

机器人三维模型采用1 ∶1 建模（图1），其外形尺寸为1.5 m×1.2 m×0.8 m，设置各部件的材料属性，得到机器人机体总质量m5约为226 kg，机体总排水量φ约为0.35 m3，进而通过式（1）求得机体所受浮力F1约为3 430 N，故2 个姿态活塞缸满载充水重力应大于1 215.2 N。

式中：ρ为水的密度，取1.0×103kg／m3；g为重力加速度，取9.8 N／kg。

图3 为姿态调节模型，基于2 个姿态活塞缸结构建立非惯性机体坐标系O－XYZ，以2 个姿态活塞缸轴心所在平面为XOY平面，并以初始状态2 个活塞缸的几何中心为坐标原点。 为便于控制，通过配重使重心和浮心均位于机器人机体几何中轴线上。充水前机体初始重心为G0（0， 0，－l3），初始浮心为F0（0， 0，－l2），坐标单位为m。 为提高系统稳定性，将机器人重型设备安装在低位，确保充水前后机器人初始重心G0处于初始浮心F0下方（即l3≥l2）。

图3 姿态调节模型Fig.3 Attitude regulation model

根据初始设计方案，活塞缸直径d0＝0.3 m，活塞缸长度l＝1.4 m，弹簧腔长度l1＝0.2 m，前腔初始长度为a1＝a2＝a3＝a4＝0.2 m。 充水结束后机器人处悬停状态，此时a1＝a2＝a3＝a4＝a0＝0.435 m，对应的m1、m2、m3、m4初始值m0＝31 kg。

此时机器人在水下处于悬停状态。 以前后侧倾状态为例，由式（2）求得理论上可产生最大倾覆力矩约为312 N·m，满足机器人姿态调节要求。

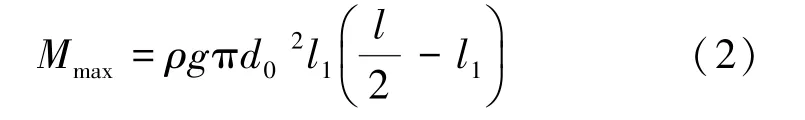
2 姿态调节系统理论模型

2.1 姿态调节模型

如图3 所示，设机器人重心为G（x，y，z），重心坐标x、y、z可根据式（3）计算得到，单位为m。

式中：mi（i＝1，2，3，4）分别为左右姿态活塞缸前后腔水体质量，kg；xi、yi、zi（i＝1，2，3，4）分别为左右姿态活塞缸前后腔水体重心坐标，m。 故可得：

式中：ai（i＝1，2，3，4）分别为左右姿态活塞缸前后腔长度，m。 充水下沉过程结束后，各部分水体总质量保持不变，即：

式中：M为姿态活塞缸充入水的总质量，kg。

弹簧腔和中间活塞质量相较前后腔水体质量太小可忽略不计，结合式（3）—式（5）可得：

式中：b0为姿态活塞缸间距，m。 机器人姿态角与重心位置关系如图4 所示，图4 中θ1和θ2分别为前倾姿态角和左倾姿态角。 在前后侧倾姿态调节过程中，设左姿态活塞缸前腔活塞位移为s，可得：

图4 姿态角与重心位置关系Fig.4 Relationship between attitude angle and gravity center

将式（7）代入式（6）可求得机器人重心坐标为

机器人姿态调节趋势为浮力和重力方向位于同一竖直线上，故结合式（5）和（8），可得前倾姿态角θ1为

以向左侧倾为例，将右姿态活塞缸前腔和后腔的水分别抽送至左姿态活塞缸前腔和后腔，此时左姿态活塞缸2 个弹簧腔继续被压缩。 设此时左姿态活塞缸前腔位移为s，可得：

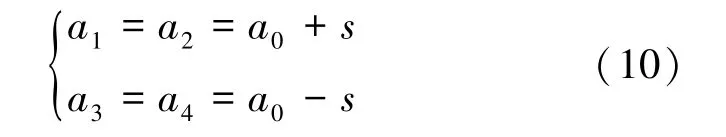
将式（10）代入式（6）可得：

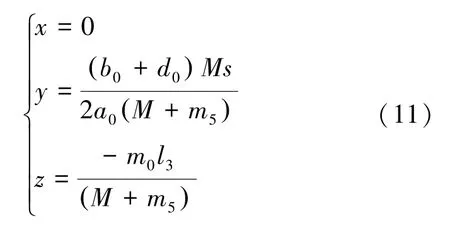
同样的根据浮心和重心位置结合式（5）和式（11），可得左倾姿态角θ2表达式如下：

2.2 系统仿真模型

利用AMESim 软件建立液压系统仿真模型，并根据式（9）和式（12）的建立参数模型嵌入仿真系统中，得到完整的姿态调节系统仿真系统如图5所示，图中位移传感器可以实时监测姿态缸活塞的位置参数。 系统的初始仿真参数见表2，仿真系统中设置4 个可独立调整变量，即活塞缸总长l、活塞缸间距b0、活塞缸直径d0和浮心z向坐标l2。节流阀jn（n＝1，2，3，4，5，6，7）等效替代六位六通控制阀，节流阀与六位六通控制阀的等效关系见表3。

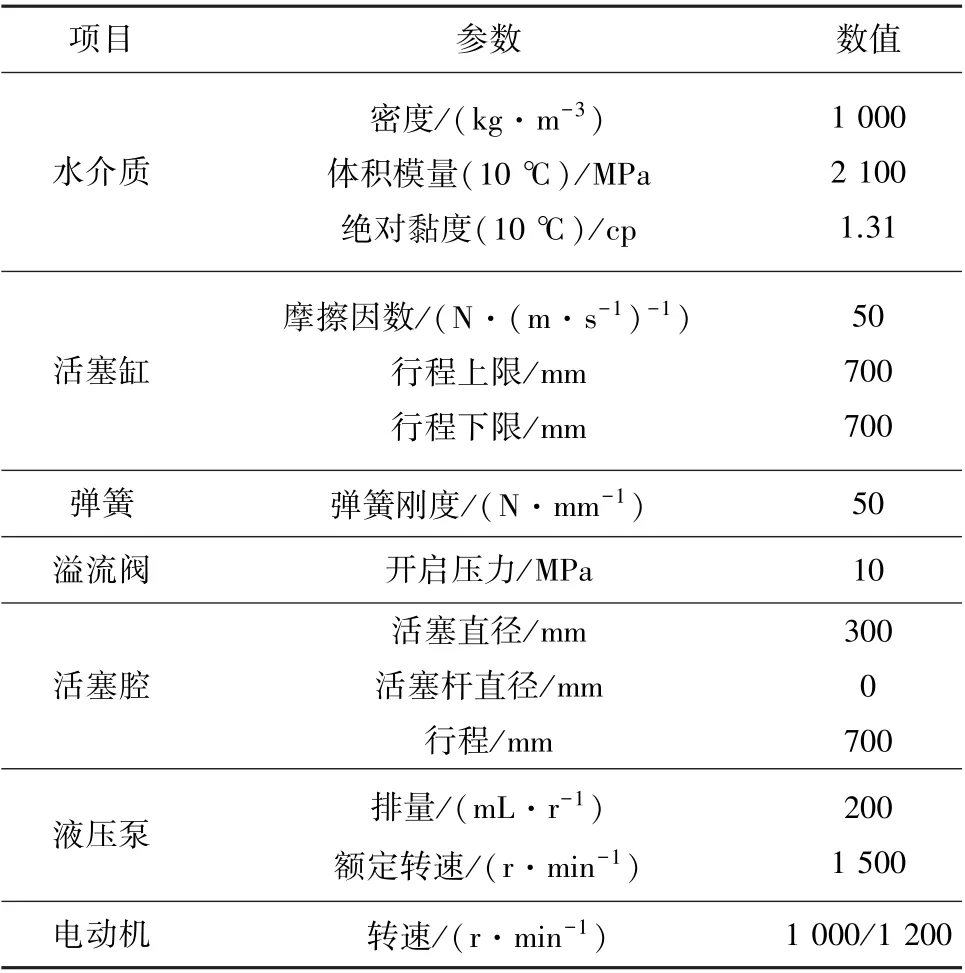
表2 系统初始仿真参数Table 2 System initial simulation parameters

表3 六位六通控制阀的等效建模Table 3 Equivalent modeling of 6－position 6－way control valve

图5 姿态调节液压系统仿真模型Fig.5 Simulation model of attitude regulation hydraulic system

3 AMESim 建模与分析

3.1 系统姿态调节过程

由于机器人的重心和浮心的设置，机器人前倾与后倾过程相反，左倾与右倾过程相反，而对角倾为前后倾与左右倾的叠加，为此，仿真仅考虑前倾和左倾两种姿态调节过程。 图6 为机器人在“充水－前倾－回正－左倾”过程中左姿态活塞缸前腔活塞位移s变化曲线。 由于机器人姿态缸尺寸均相同且姿态缸对称布置，姿态活塞缸前、后腔活塞位移也对称或同步变化，因此仿真计算仅给出左姿态活塞缸前腔的活塞位移曲线。

由图6 可知，在t＝0～20 s 为充水（下沉）过程，弹簧腔被压缩，前腔活塞位移达到0.235 m（前腔初始长度设置为0.2 m），充水阶段结束后前腔长度达到0.435 m，与设计参数相一致。 在t＝25 ～75 s，六位六通控制阀处于f 锁紧位，各缸锁止；在t＝25 ～75 s，机器人先前倾后回正，前腔活塞跟随中间活塞做往复运动，弹簧腔不被压缩，最大位移达到0.67 m；在t＝75 ～90 s，右姿态活塞缸前腔和后腔的水被分别抽送至左姿态活塞缸的前腔和后腔，左姿态活塞缸弹簧腔继续被压缩，则机器人左倾。

图6 左姿态缸前腔活塞位移Fig.6 Piston displacement in front chamber of left cylinder

仿真结果表明，通过控制姿态活塞缸的储水量可方便实现机器人的姿态调节。 图6 仿真曲线与预期的设计方案相吻合，满足了设计要求。 为优化姿态调节过程，采用单因素分析，得到不同活塞缸总长l、活塞缸间距b0、活塞缸直径d0和浮心z向坐标l2等结构参数对姿态调节过程的影响。

3.2 浮心z 向坐标l2的影响

设置l＝1.4 m、b0＝0.5 m、d0＝0.3 m，浮心z向坐标l2依次取0.1、0.15、0.2、0.25、0.3 和0.35 m，得到第1 组参数下，浮心z向坐标l2对前倾姿态角θ1和左倾姿态角θ2的影响规律分别如图7 和图8 所示。

图7 浮心z 向坐标对前倾姿态角的影响Fig.7 Influence of l2 on forward attitude angle

由图可知，当浮心z向坐标l2＜0.3m 时姿态角随着前腔活塞位移s的增加近似线性增大，但此时前腔活塞位移s的变化对姿态角的调节作用不明显，调节的灵敏度较小，同等姿态角需要更大的活塞行程，考虑到调节的灵敏性及实际活塞行程的限制，浮心z向坐标l2应取较大值，尤其是l2＞0.3 m 时，同等活塞位移下前倾姿态角θ1和左倾姿态角θ2大幅增加。 此外，对比图7 和图8 可知，调节同等活塞位移s的情况下，获得的左倾姿态角θ2要比前倾姿态角θ1大，其主要是由于机器人在x向的尺寸较大所致。 因此，设计时可通过缩短x向尺寸提高纵倾调节的灵敏性。

图8 浮心z 向坐标对左倾姿态角的影响Fig.8 Influence of l2 on left－leaning attitude angle

同时，由式（9）和式（12）可知，为保证系统空间姿态的稳定性，浮心z向坐标l2还需满足式（13）的约束关系，由式（13）求得l2＜0.38 m。

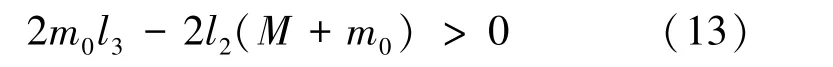
综合考虑以上因素，取l2＝0.35 m，此时无论是纵倾还是横倾的姿态倾角调节均较为灵敏，姿态角的调节范围大，且系统稳定性也可以得到保证。

3.3 活塞缸直径d0的影响

设置l＝1.4 m、b0＝0.5 m，取浮心z向坐标l2＝0.35 m，活塞缸直径d0依次取0.25、0.27、0.29、0.31、0.33 和0.35 m，得到第2 组仿真参数下活塞缸直径d0对前倾姿态角θ1和左倾姿态角θ2的影响规律，分别如图9 和图10 所示。

图9 活塞缸直径对前倾姿态角的影响Fig.9 Influence of d0 on forward attitude angle

图10 活塞缸直径对左倾姿态角的影响Fig.10 Influence of d0 on left－leaning attitude angle

由图9、图10 可知，不同活塞缸直径d0下前倾姿态角特性曲线比较分散，而左倾姿态角特性曲线相对集中。 当活塞缸直径d0较小时，姿态角随着前腔活塞位移s的增加而近似线性增大，且同等活塞位移下左倾姿态角θ2的值明显大于前倾姿态角θ1的值。 为提高前倾调节的灵敏性，活塞缸直径d0应该取较大值，但随着活塞缸直径d0的增大，尤其是当d0≥0.31 m 后，继续增大活塞缸直径d0对前倾姿态角θ1的增大作用逐渐减小。 且过大的活塞缸直径d0还会导致活塞缸尺寸布局不合理。

综合考虑以上因素，取活塞缸直径d0＝0.33 m，此时无论是纵倾还是横倾的姿态角调节均较为灵敏，姿态角的调节范围大，且系统稳定性也可得到保证。

3.4 活塞缸间距b0的影响

设置l＝1.4 m，d0＝0.33 m，l2＝0.35 m，活塞缸间距b0依次取0.10、0.20、0.30、0.40、0.50 和0.60 m。由式（9）和式（12）可知，活塞缸间距b0只对左倾姿态调节产生影响，对纵倾调节无影响。 因此，只需考虑活塞缸间距b0对左倾姿态角θ2的影响，得到第3组参数下的仿真结果如图11 所示。

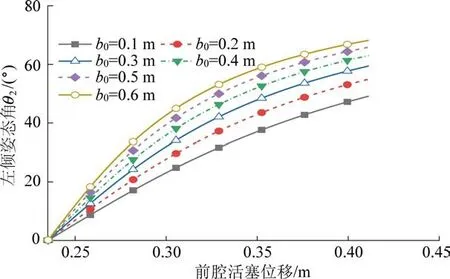
图11 活塞缸间距对左倾姿态角的影响Fig.11 Influence of b0 on the left－leaning attitude angle

由图11 可知，左倾姿态角θ2随着活塞缸间距b0的增大，其值随着前腔活塞位移的增大响应越来越快，但随着活塞缸间距b0增大，特性曲线越来越密集，可见继续增大活塞缸间距b0对姿态角的影响越来越小。 且过大的活塞缸间距b0会导致机器人的横向尺寸过大，考虑到结构布局合理和调节效率，选取b0＝0.60 m。 此时横倾姿态倾角调节均较为灵敏，且姿态角调节范围大，左倾姿态角θ2最大值达到68.20°。

3.5 活塞缸总长l 的影响

设置d0＝0.33 m、l2＝0.35 m、b0＝0.5 m，活塞缸总长l依次取1.20、1.30、1.40、1.50、1.60 和1.70 m，并将姿态活塞缸中间活塞尺寸做适应性调整以确保其他参数不变。 由式（9）和式（12）可知，活塞缸总长l只对纵倾姿态调节产生影响，对横倾调节无影响。 因此，仅需考虑活塞缸总长l对前倾姿态角θ1的影响，得到第4 组仿真参数下的特性曲线如图12所示。

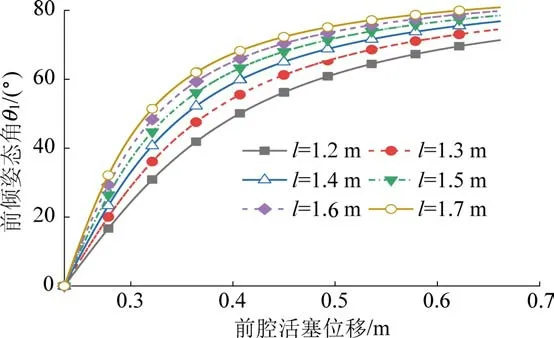
图12 活塞缸总长对前倾姿态角的影响Fig.12 Influence of l on the forward attitude angle

由图可知，当前腔活塞位移s≤0.4 m 时，前腔活塞位移s的增加对前倾姿态角θ1的增大作用较大，但当前腔活塞位移s＞0.4 m 后，继续增大前腔活塞位移s对前倾姿态角θ1的影响逐渐减弱。 而增加活塞缸总长l有助于提高姿态角调节的灵敏性，但姿态角特性曲线总体比较密集，随着活塞缸总长l的增大，姿态角的增加幅度越来越慢。 且过大的活塞缸总长l会导致机器人的纵向尺寸过大，考虑到结构布局的合理性并兼顾调节效率，选取l＝1.5 m。此时纵倾姿态倾角调节较为灵敏，姿态角调节范围大，前倾姿态角θ1最大值达到78.46°。

为便于对比上述4 组仿真最终优选的结构参数对姿态角的影响效果，得到活塞位移在0.235 ～0.4 m对应的姿态角特性曲线如图13 所示。 由图13可知，上述4 组仿真按照单因素对比分析，得到的倾角范围逐步增大。 以活塞位移s＝0.4 m 为例，第1组对比分析得到θ1，max＝46.10°，θ2，max＝59.00°；第2组对比分析得到θ1，max＝58.76°，θ2，max＝64.42°；第3组对比分析得到θ1，max＝58.76°，θ2，max＝66.87°。 最终在第4 组 对 比 分 析 得 到θ1，max＝62.24°，θ2，max＝66.87°，前倾姿态角θ1和左倾姿态角θ2的范围均得到大幅提升。

图13 4 组优选参数对姿态角的影响Fig.13 The influence of 4 groups parameters on attitude angle

4 结 论

1）为满足关停矿井资源化利用与绿色开发的需求，以及绿色液压传动发展趋势，煤矿抽水蓄能电站水下巡检机器人的姿态调节系统采用无油压传动设计，整个液压系统均以水为传动介质。

2）机器人的重、浮心采用居中设计，两多腔姿态活塞缸采用对称布置，且沉浮调节时姿态活塞缸分别与外水体环境进行介质传递，而姿态调节时水介质在姿态活塞缸内部传递，简化了姿态调节系统结构，提高了姿态调节的效率和稳定性。

3）增大活塞缸直径、浮心z向坐标、活塞缸总长及活塞缸间距均有助于提高姿态调节的灵敏性；同等活塞位移下横倾（左倾）姿态角要明显大于纵倾（前倾）姿态角；浮心z向坐标越大，其对纵、横倾姿态角的影响作用越明显；活塞缸直径越大，其对纵倾姿态角的影响越小；活塞缸总长仅对纵倾产生影响，而活塞缸间距仅对横倾产生影响。

4）活塞缸直径d0＝0.33 m，浮心z向坐标l2＝0.35 m，活塞缸间距b0＝0.5 m 且活塞缸总长l＝1.50 m时，机器人的纵、横姿态倾角调节均较灵敏，且倾角调节范围大，前倾姿态角θ1最大值为78.46°，左倾姿态角θ2最大值为68.20°。