一种融合区域生长和RANSAC的稠密点云平面分割方法
张建伟,权庆乐
(河南牧业经济学院 信息工程学院,河南 郑州 450004)
0 引 言
近年来,随着三维激光扫描技术的快速发展,高精度、数据海量的稠密点云已广泛应用于逆向工程[1]、文物修复[2]、3D打印[3]、自动驾驶[4]等领域。如何从点云中快速、准确地提取出真实场景目标信息,已逐渐成为国内外众多学者的研究热点。平面结构由于具有良好的几何特性,广泛地存在于室内外各场景中。鲁棒的平面结构可为场景结构建模[5]、机器人导航定位[6]等提供稳定的特征信息。稠密点云由于其数据细节丰富,可以较为鲁棒地反映真实地物信息,但由于其数据海量,如何高效准确处理成为难题。因此稠密点云中快速准确地提取平面结构已成为计算机领域中重要的研究内容[7-8]。
国内外众多学者针对平面提取已做了部分研究,而目前的平面分割方法可总体分为模型拟合类方法、深度学习类方法和区域生长类方法。
1)模型拟合类方法。主要包括随机采样一致性算法(RANSAC)[9-10]和霍夫变换算法(Hough transformation)[11]。RANSAC算法首先预先设定平面参数,依据点到平面的距离,在全局范围内将三维点分为外点与内点,并将内点数最多的点集作为最终平面分割结果。部分学者对RANSAC方法进行改进,SCHNABEL等提出采用八叉树优化RANSAC算法,以提高平面提取效率[12]。熊风光等提出将K均值聚类与RANSAC相结合,以提高算法中的粗差点剔除率,在一定程度上提高了RANSAC算法的准确度[13]。RAGURAM等采用附加法向矢量的方式提取数据中的三角面片。以上方法虽然有较好的抗噪性,但计算效率较低,同时未考虑空间连通性,易在稠密点云数据中产生伪平面[14]。
霍夫变换算法将原始空间中平面检测问题转化为寻找参数空间峰值问题。目前主要模型有球体、直线、柱体和平面等。田朋举等提出一种基于2DHough变换和八叉树相结合的方法,实现建筑平面的有效分割[15]。HULIK等采用矢量约束来提高Hough变换算法检测平面的准确度。但该类方法存在一定的平面误识别现象[16]。
2)深度学习类方法。通过构建卷积神经网络,对点云数据进行语义信息分割。以PointNet[17]、PointNet++[18]、PointCNN[19]等深度神经网络为代表,可有效实现在真实场景下,提取点云数据中平面结构。YU等针对稀疏点云特性,提出网络模型,提高平面拟合精度,但在稠密点云数据中的计算效率仍有待提高[20]。该类方法需大量样本清洗及模型训练等工作,当处理大规模稠密点云时,与传统方法相比并无显著优势。
3)区域生长类方法[21-22]。通常是利用法线、曲率等几何属性,分析点云局部空间的邻接关系,进而实现平面点云的生长。薛婧雅等提出基于超体素与区域生长相结合的方式提高屋顶平面的分割精度[23]。王冲等采用动态分配权重的方法来提高法线解算精度,进一步提高区域生长算法的准确性[24]。FOTSING等采用ICP算法选取可靠的候选种子点,并在生长过程中采用体素表达点云,改善平面分割质量[25]。ZHANG等提出一种基于2D和3D相互投影的区域生长方法,通过点云以及投影平面的几何信息选取初始种子点,并通过区域生长条件判断每个点的通视性,改善分割效果[26]。该类方法提取平面精度较高,但受到区域生长条件限制,平面结构的完整度有待提高。同时该方法更关注于点云局部空间变化,对于平面结构的整体考虑不足。
近年来一些学者也提出一些新方法,ZHU等将平面分解为多个平面段合并的结果,采用准逆理论(quasi-a-contrario theory)利用误警值(false alarms)评估每个平面段的分割效果[27]。WANG等用L0梯度最小化算法的区域生长以及图分割(graph cut)提取物体表面[28]。FATEMEH等提出多平面算法用于区分多平面立面的结构和非结构元素,从统计上考虑点组相对于其邻居的位置,以进行识别的隔离多平面建筑的主立面[29]。
目前众多研究方法多集中于某一类平面分割方法,并在此基础上进行优化,而忽略各类方法之间的关联性。模型拟合类方法具有严格的数学模型,但是忽略了局部空间结构的连续性。区域生长类方法强调局部空间中连续,而未对数据进行整体限制考虑,而过于严格的曲率阈值则会导致平面结构的不完整。因此,综合以上各类平面分割方法的特点,提出一种区域生长和RANSAC相结合的稠密点云平面分割方法。融合2类平面分割方法中数学模型以及局部空间约束的优点,克服空间不连续及平面完整度不高的缺点。首先采用3种滤波方法实现点云初步的预处理,然后采用混合区域生长算法实现平面结构的初分割,其次利用平面弯曲度约束对平面结构的几何状态进行判断,最后采用RANSAC算法剔除异常平面的粗差点,从整体提高平面分割的准确度。该方法综合RANSAC和区域生长平面分割方法的优点,在一定程度上提高平面分割的准确度与完整度。
1 平面分割方法
1.1 技术路线
平面分割技术路线如图1所示。首先对原始稠密点云进行预处理,利用无效点剔除、统计滤波、体素滤波,显著降低点云数据量,滤除大量离群噪声点。然后提出一种混合区域生长分割方法实现场景中平面点云的初分割。其次以整个平面为基础对平面进行弯曲度约束分析,检测出弯曲度异常平面。最后采用RANSAC算法剔除平面粗差点,提高平面分割准确度和完整度。
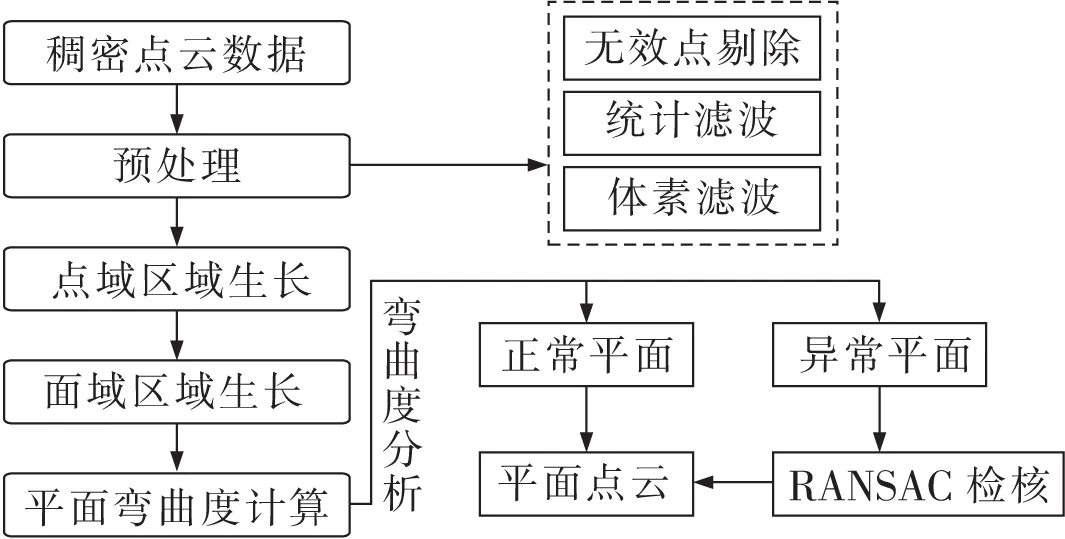
图1 稠密点云平面分割技术路线Fig.1 Pipeline of plane segmentation for dense point cloud
1.2 数据预处理
由于稠密点云数据海量,对其直接处理,严重影响处理效率,因此在平面分割前对其进行预处理,为后续平面特征提取做准备。
首先对稠密点云数据P进行数据格式检查,寻找数据中存在的“非法”格式,如点云中常见的“NAN”,并对其进行剔除。然后采用统计滤波滤除噪声点,其原理如公式(1)所示。最后采用体素滤波,在保证点云数据整体轮廓的前提下,降低点云数据量,其中体素滤波采用边长为l(0.02 m)的三维网格。在预处理后得到点云数据PV。
(1)

1.3 点域区域生长
在预处理后,以三维点为基础,结合局部邻域空间分析,制定邻域生长条件,进行点域内的区域生长。主要包括以下步骤。
1)采用Kd-tree在PV中为所有三维点确定邻域点集Gi={pk}。
2)构建邻域协方差矩阵,采用特征值分解,计算其特征值λ1,λ2,λ3和对应特征向量ξ1,ξ2,ξ3(λ1>λ2>λ3),ξ3作为该点法线,计算曲率V如下
(2)
3)根据曲率值V,对所有点升序排序。按曲率顺序,依次遍历每一点,并初始化种子队列seeds,计算每一个种子点与各自邻域点法线夹角。
4)若种子点法线与种子点法线夹角小于阈值ϑ(3°),则将当前邻域点加入种子点seeds,若夹角大于ϑ,继续其他邻域点计算。
5)若当前种子队列均判断完毕,则输出当前平面点云plj。
6)遍历PV所有点,直到所有点均已判断完毕,见式(3)将PV分为剩余点云Ple、平面点云集{plj}。
(3)
式中n为平面数量。
1.4 面域区域生长
由于区域生长条件的限制,点域区域生长后的剩余点云Ple中仍包含部分属于但未被归类到相应平面结构的三维点。文中进一步采用面域区域生长进一步处理未分类的平面点。图2为面域区域生长的示意,主要包括以下步骤。
1)平面筛选。琐碎的平面点云,通常并非真正的实体结构,或对场景结构的表达的意义不大。因此如图3所示,对于提取的平面点云,通过外接矩形面积近似作为平面点云面积,并经验性地设置面积阈值s(0.02 m2),剔除面积较小的平面,将其放回至剩余点云Ple中。
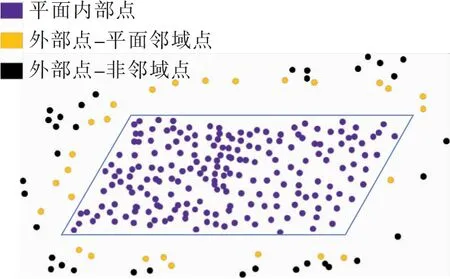
图2 平面区域生长Fig.2 Planar region growing
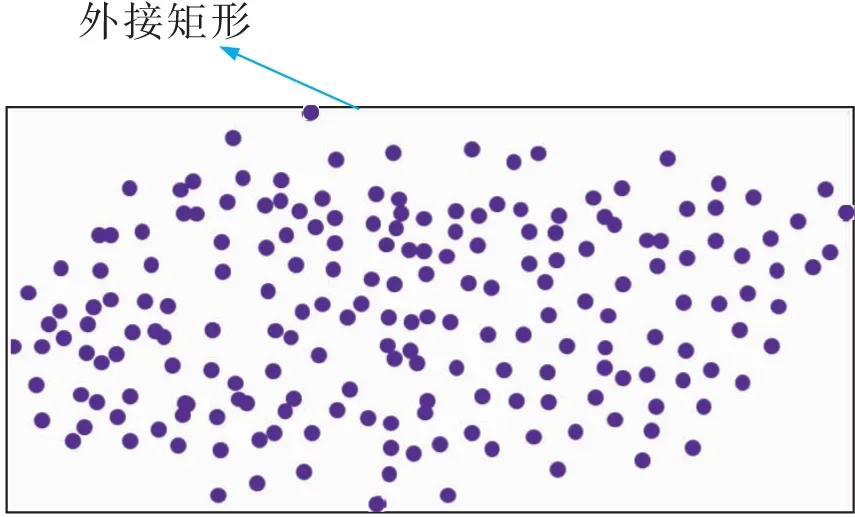
图3 外接矩形Fig.3 Bounding rectangle
2)建立邻域结构。以平面为基础,再次采用KD-tree在剩余点云中,对平面点云建立邻域结构,并去除重复的邻域点(图2中黄色点)。
3)平面生长。在每一个平面邻域中,计算其到平面的距离,若小于距离阈值d1(0.03 m),则将其归类为当前平面点云。
1.5 平面弯曲度约束
平面分割后,以每一平面点云为基础,计算平面的整体平均曲率,将其作为整个平面的弯曲度评价指标,主要包括以下步骤。
1)在公式(4)中,采用最小二乘法拟合平面方程,并计算整个平面点云重心点pc。
(4)
式中a1,…,a6为拟合的平面方程参数。
2)在公式(5)中,基于参数方程的一阶、二阶偏导、获得pc处拟合曲面的第1基本量(E,F,G)和第2基本量(L,M,N)。
(5)
式中n为法向量。
3)在公式(6)中,结合参数方程计算出主曲率ρ1ρ2、平均曲率H。若重心点的平均曲率绝对值小于曲率阈值ε(0.4),为正常平面,否则将其标注为弯曲度异常平面。
(6)
1.6 RANSAC检核平面
平面弯曲度约束分析后,平面点云分为正常平面和弯曲度异常平面。如图4在异常平面中采用RANSAC拟合平面点云方程,并计算整体平面的点云的误差,将点到平面距离大于阈值d2(0.02 m)的点,作为粗差值点,进行剔除,提高平面分割准确度。而弯曲度正常平面则无需进行RANSAC检测,可认为其已基本满足几何一致性原则,直接保存为最后的平面分割点云。最后输出所有平面点云。

图4 RANSAC检核平面Fig.4 Check plane with RANSAC
2 实验结果与分析
2.1 实验数据与环境
实验环境为Intel Core i7-5500U CPU@2.40 GHz 2.39 GHz,8.0 GB RAM,采用Ubuntu 16.04系统,C++编程实现。实验采用4组数据,其中前2组数据来自PARK学者公布的公寓及阁楼场景点云数据[30],后2组数据来自苏黎世大学(UZH)的可视化与多媒体实验室提供的办公室扫描数据(https://www.ifi.uzh.ch/en/vmml/research/datasets.html)。
图5是采用文中预处理方法后的点云结果,体素滤波采用边长为0.02m的三维体素网格进行体素化处理。从图中预处理效果可以看出,在保持整体场景特征信息的前提下,点云数据量在一定程度上有所降低、大部分离群噪声点得到有效剔除。

图5 实验数据Fig.5 Experimental data
2.2 平面分割对比实验
在平面分割实验中,选取传统的区域生长和RANSAC方法作为对比实验。各方法的分割效果如图6所示,其中不同颜色表示不同平面点云。从图中分割效果可以看出,RANSAC方法仅使用数学模型对点云进行分割,未能保证平面点云的连通性,致使多处不邻的平面段误识别为同一个平面点云。区域生长方法的分割效果总体较为良好,但平面分割受到生长条件的限制,未能保证平面的完整度,位于平面边缘附近的点云未能很好进行归类。目视效果上可见,文中方法可提取处场景中的大部分平面,同时平面之间的边缘点云也得到良好归类,平面结构的区分度较高,在保证准确度的同时也保证了平面结构的完整度。

图6 平面分割对比Fig.6 Comparison of plane segmentation
2.3 未分类点分布
为进一步对比分析平面分割方法性能,如图7提取出各方法分割后未归类到具体平面的剩余点云。在剩余点分布方面,RANSAC方法由于仅采用空间数学模型,保留剩余点数量最少。其次是文中方法,最后是传统区域生长方法。相比于区域生长方法,文中方法可以更好地处理平面边缘点,减少剩余点数量,提高平面完整度。
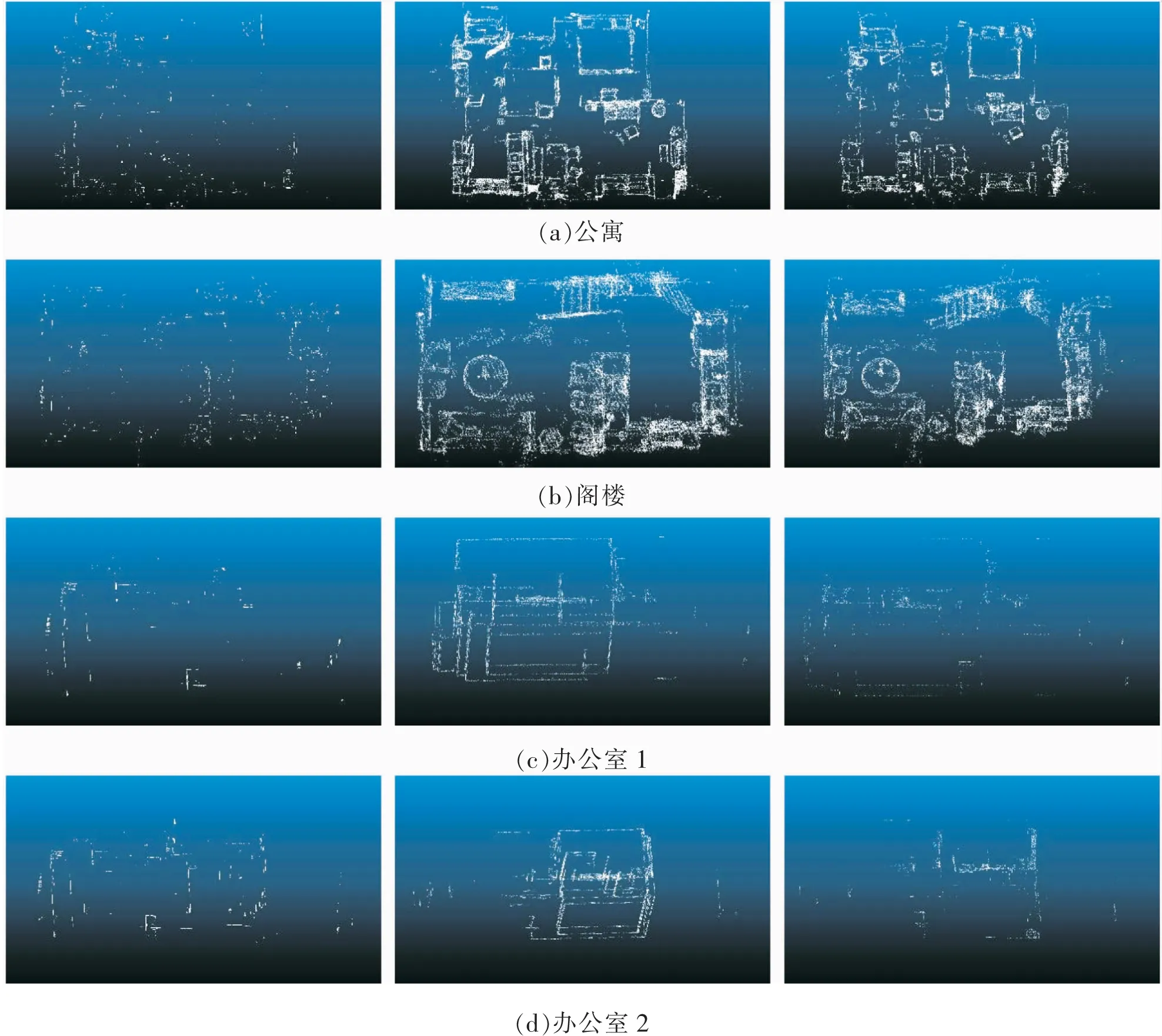
图7 未分类点分布Fig.7 Distribution of unclassified points
2.4 精度评估
进一步量化分析分割方法的性能,采用式(7)和式(8)中准确度(Corrrectness,Cr)、完整度(Completeness,Cm)[31]指标评估各算法。实验中采用CloudCompare软件的标记功能,勾选数据中的平面点并添加Label作为评估的真值。
(7)
(8)
式中TP为正确分割平面点;FP为错误识别的平面点;FN为漏检的平面点。
表1记录了实验中3种分割方法在4个数据的分割结果的平面数量、剩余点数、准确度和完整度。其中RANSAC方法由于空间几何模型在全局范围提取平面,可提取出场景中的绝大部分平面点。但由于实验数据中存在大量的平面,致使RANSAC方法所提取的大部分平面点是空间非连续的,这与空间平面的几何属性相矛盾。区域生长方法和文中方法所分割平面均由空间连续三维点构成,符合空间平面的几何特性。同时相比于区域生长方法,文中方法在准确度与完整度方面均所有提升,4个场景中准确度均提升2%左右,均达到95%以上。完整度提高效果为:公寓场景提升约20%;阁楼场景提升约27%;办公室1场景提升约12%;办公室2场景提升约11%。文中方法更加鲁棒地提取稠密点云中的平面结构,并提高平面特征的完整度。为后续场景建模以及机器人定位导航提高更加鲁棒的特征结构。

表1 平面分割量化统计Table 1 Quantitative statistics of plane segmentation
3 结 论
1)利用点域内区域生长和面域内区域生长相结合,可以有效克服传统区域生长在平面边缘分割时的欠分割现象,平面分割的完整度提高约17%。
2)采用曲率值近似表达平面弯曲度,并对所分割的平面点云进行检核,可以有效检测出异常弯曲的平面,有利于检测平面中的粗差点。
3)利用RANSAC检核平面,可以在保证平面分割的连通性的基础上,进一步提高平面分割的准确度,在典型的室内场景中,分割的准确度可达到95%。
4)基于稠密点云数据的平面分割方法可为基于平面结构的特征建模以及室内机器人导航定位提供可靠的特征基础。

