环形柔性结构四点悬吊设计方法及试验研究

马国亮，杨津浦，田建辉，韩兴本

（1.西安工业大学 机电工程学院，陕西 西安 710021；2.上海航天电子技术研究所，上海 201109）

0 引言

环形桁架天线是当今空间大口径卫星天线的主流形式，环形天线的口径从几米到上百米，美国很多电子侦察卫星上的天线均采用了这种结构形式，我国也正在研究此类大口径天线。环形天线的结构尺寸大、柔性大，导致固有频率很低，一旦受到扰动，因阻尼弱而衰减缓慢。能否快速、有效地抑制有害振动是保障卫星安全的关键，对提高卫星工作品质、延长结构寿命、节省姿态调整能量等具有重要的科学意义和经济效益。

空间环境对航天器的影响有热激励、宇宙射线、空间碎片等，最明显的是低重力影响，因此，在进行地面振动试验时，消除地面重力的影响尤为重要。在发射航天器前的地面试验中，由于重力作用，环形天线等卫星柔性附件会产生严重的静态变形，增加试验难度，影响试验的准确性。面对无法避免的重力因素影响，只有完成重力卸载或低重力模拟后再进行振动试验才具有实际意义，而通过悬吊法实现环形天线重力卸载是亟待解决的技术难题。

自低重力模拟技术问世以来，悬吊技术引起了国内外学者和研究机构的关注，并开发了很多实用系统。如美国NASA研制的自由度低重力悬吊模拟系统，采用主动伺服控制吊索对人提供拉力和位移，用于训练宇航员的行走活动；美国科罗拉多大学的GRESCHIK 等提出了一种支撑重量的“牵线木偶”式悬吊装置，在兰利研究中心得到了验证；英国剑桥大学设计的可折叠太阳翼展开机构采用被动跟随的方法进行低重力实验，恒力吊索的长度几乎不变。利用气体的可压缩性实现悬吊，如美国和加拿大提出了气动弹簧悬吊系统。国内对低重力模拟和悬吊装置的研究起步较晚，但随着航天发射任务的猛增，我国悬吊装置的技术水平已接近甚至超过欧美日等国。哈尔滨工业大学的刘振等为航天五院研制了一种星球车重力补偿系统，基于单吊索主动跟随方式，实现了重力补偿；上海宇航系统工程研究所的吴松等悬吊了一个柔性结构，分析了水平和垂直基频误差。聚焦卫星环形天线结构的悬吊和振动特性研究，西安交通大学的罗亚军等开发了一种单吊索悬吊装置，实测得到了环形柔性结构水平方向的“摇头”模态；郑宜生等提出了一种多点负刚度磁弹簧悬吊装置，能够平衡环形柔性结构的重力，且在水平方向只有很小的附加约束，使“摇头”频率接近无重力时的频率；北京航空航天大学的唐锐等设计了一种可调节平衡位置和几何参数的准零刚度悬吊装置，具有较大的承载能力；天津大学的彭浩等提出了一种水平定位和运动的重力补偿方法，在天线展开过程中实现了滑轮车对桁架节点位置的精确跟随；作者设计了环形柔性结构的“三点”悬吊装置，静力学方程是静定的。以上研究提出的悬吊方法能够实现对航天器柔性结构的重力卸载或低重力模拟，但对于环形天线结构，多点悬吊装置存在超静定问题，且多点悬吊后“点头”模态的实现问题有待深入研究。

本文以环形柔性结构的悬吊装置为研究对象，根据环形柔性结构不同模态振动方向的特点，采用吊索悬吊的方式，设计四点悬吊装置；通过力学分析解决超静定问题，形成悬吊设计的基本方法，并完成四点悬吊装置的设计和模态测试，实现环形天线结构悬吊后不同模态振动，包括“点头”模态和“摇头”模态，具有一定的实际应用价值。

1 四点悬吊装置的力学建模

由于重力的作用，柔性环形天线安装在地面上，静态变形大，采用悬吊电机输出恒力的方式来平衡重力。设环形天线结构在多点悬吊后，处于水平状态，悬吊点数量一般根据天线的节点决定，如图1 所示。图中，为支撑臂的质量，为环形天线的质量，为环形结构的直径，m为悬吊电机线圈的质量，f为摩擦力，M、N和N为支撑臂根部的支反力，F为悬吊电机输出的安培力。

图1 环形天线结构悬吊示意图Fig.1 Suspension diagram of the hoop antenna structure

悬吊结构的力系由重力、摩擦力、悬吊电机输出的安培力和支反力等组成，当力系达到静态平衡时，根据平面力学分析可知，在、方向和绕点存在以下3 个平衡方程：

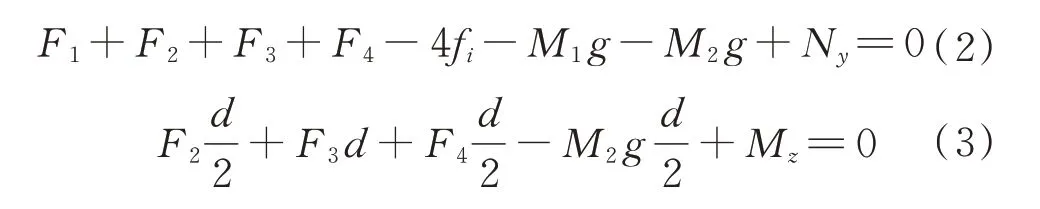
以四点方式进行悬吊设计，由于悬吊装置的对称性，可知=；结构光滑时无摩擦力，未知量有5 个，但只有2 个独立的方程，这组方程不是静定方程，结构是三次超静定结构；又因重力卸载时，N为0 或为0，M为0，此时，未知量有3 个，结构为一次超静定结构。下面通过2 种方法进行分析。

1）应用变形比较法，如图1 右上所示受力分析示意图，均布载荷=/，解除和处的约束，等效为多余约束力和。在结构悬吊平衡后，在、和均布载荷作用下，和处的挠度为0，即变形条件为

式中：多余约束力、和均布载荷产生的挠度为

式中：、为修正系数；为结构弯曲刚度，当=/2时，代入变形条件得到，再代入平衡方程得到。

2）如图1 右下所示一维梁模型，在和的作用下恢复平衡，恢复的挠度为；设和处悬吊点为多余约束点时，环形结构在的作用下恢复平衡，恢复的挠度为，挠度分别写作

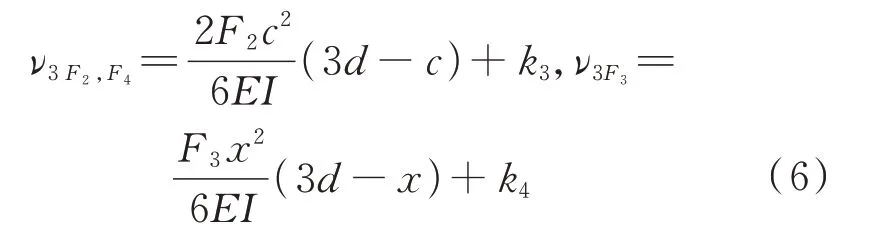
式中：、为修正系数。根据变形协调关系，在环形结构平衡后，处的挠度应为0，且处单独由、和恢复的挠度应该相等：

当=、=/2时，代入挠度得到、的关系，统一将安培力的关系写为

式中：为待定系数。

在振动试验中，悬吊电机输出安培力和信号源的电压成比例

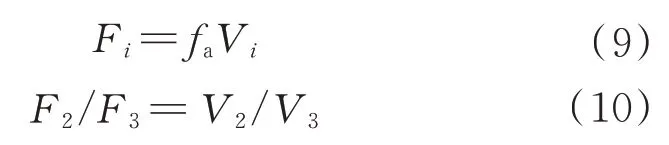
式中：为单位力；V为信号源的输出电压，即电压的比值也是安培力的比值。

2 模态分析和静态变形

实物环形天线的尺寸太大，频率很低，如南京航空航天大学戴宇航等分析了大型环形天线的模态。实验室环境中可采用相似小模型类比大结构的动力学特性，即采用缩比模型进行试验。环形柔性结构1 个缩比模型的质量为=0.350 kg，支撑臂的质量为=0.125 kg，其他几何参数见表1。悬吊电机线圈骨架为玻璃纤维，悬吊绳材料为Kevlar 纤维，和其余结构相比，可以忽略悬吊绳质量。

表1 环形柔性结构的参数Tab.1 Parameters of the hoop flexible structure

采用有限元仿真分析缩比模型的固有频率和模态振型。应用MSC Patran 建立环形柔性结构的三维模型，包含30 个节点和38 个梁单元，再应用Lanczos 解法求解振动特性。前4 阶固有振型如图2所示，前两阶固有频率分别为2.178 Hz 和2.788 Hz，属于低频振动，且前两阶模态分别为“点头”模态和“摇头”模态。因此，悬吊设计需考虑水平和垂直方向振动的影响。

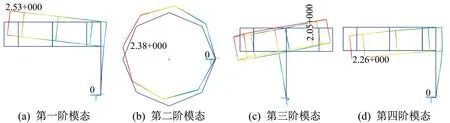
图2 前4 阶模态Fig.2 The first four modes

当无悬吊装置时，提取环形柔性结构半边环节点处的静态位移，再测量其缩比模型半边环节点处的静态位移，有限元计算和实测位移如图3 所示。有限元计算和实测静态变形结果接近，且近似是线性变形，拟合曲线分别为=0.12-0.024，=0.13-0.027。以实测结果为例，环形结构静态变形处位移为0.053 m，略大于有限元计算出的0.048 m。

图3 静态变形及曲线拟合Fig.3 Static deformation and curve fittinghang

3 多点悬吊装置试验

根据悬吊设计分析和模态分析结果，设计悬吊装置如图4 所示。

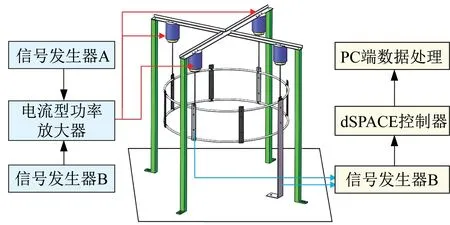
图4 振动试验示意图Fig.4 Schematic diagram of vibration test

试验装置主要包括含支撑臂的环形柔性结构、悬吊电机（XVLC70-015-00N）、四通道电流型功率放大器（西安交通大学研制）、信号发生器A（Agilent 33210A）、信号发生器 B（Keysight 33500B）、激光位移计（KEYENCE、LK-G10）和dSPACE 控制器（DS1202）等。

根据试验示意图，搭建悬吊装置实物，如图5所示。2 个信号发生器输出3 路独立的电压信号到电流型功率放大器，电流型功率放大器再输出电流信号到悬吊电机，悬吊电机输出安培力吊起环形柔性结构。激光位移计测量环形柔性结构被激振后根部和侧边振动响应，输入dSPACE 控制器，经过数据处理得到振动测试结果。在振动测试试验中，当信号发生器A 输出两路独立的电压信号（-85±3）mV 到处悬吊电机，信号发生器B 输出电压信号（-55±2）mV 到处悬吊电机时，环形柔性结构恢复平衡，此时，=，得到系数约为0.647，代入结构参数后发现其符合第2 种假设。

图5 振动试验Fig.5 Vibration test

在环形柔性结构悬吊前，分别在其端点的水平和竖直方向施加激励，通过激光位移计测量2 个方向的振动响应，如图6（a）所示。在环形柔性结构悬吊平衡后，激励并测量2 个方向的振动响应，如图6（b）所示。最后，对位移信号做傅里叶变换后得到幅频曲线，设（）为测量的振动响应，傅里叶变换为

图6 悬吊前后的振动响应Fig.6 Vibration responses before and after suspension

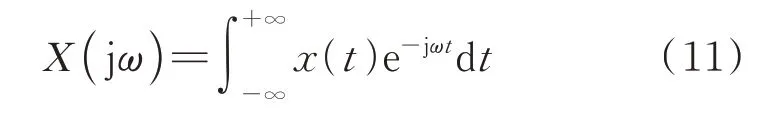
其中，振动响应为单位初始位移，初始速度和任意激励的响应之和：

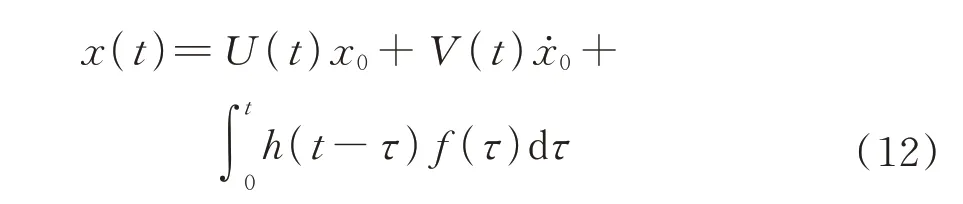
由振动响应结果可知：悬吊前，振动响应衰减缓慢；悬吊后，其衰减较快。表明在悬吊后，悬吊电机本身的阻尼特性等因素缩短了衰减过程。由固有频率可知，悬吊前，前两阶固有频率分别为2.087 Hz 和2.581 Hz；悬吊后，分别为2.294 Hz和2.534 Hz。有限元计算的前两阶固有频率分别为2.178 Hz 和2.788 Hz，略大于实测数据，说明实际模型结构的刚度可能较小，悬吊装置基本实现了悬吊要求，如图7所示。

图7 悬吊前后的固有频率Fig.7 Natural frequencies before and after suspension

在不同悬吊位置时，悬吊电机的输出力并不是恒定，会随着位置的变化而产生小幅波动。选择1个用于悬吊的音圈电机进行测试，型号为XVLC70-015-00N。力传感器为TJL-1，力测量仪为HBM，信号发生器为Keysight 33500B，电流功放为自制设备。信号发生器输出直流电压到电流功放，电流功放再输出电流到音圈电机，只需观测电压与输出力之间的关系。试验系统如图8 所示。

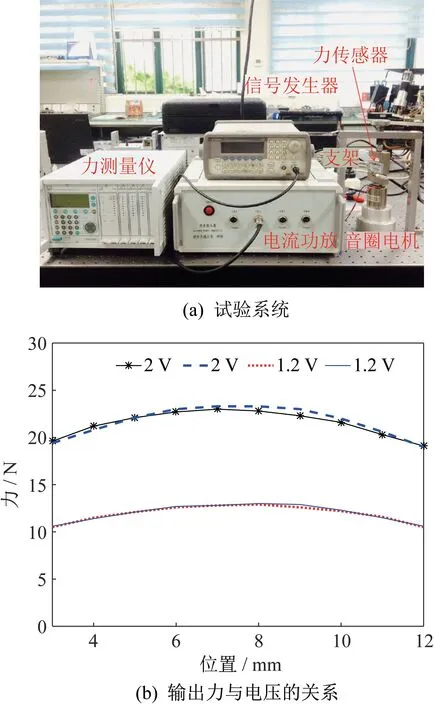
图8 音圈电机输出力试验Fig.8 Output force test of voice coil motor

由音圈电机输出力和位移的测试结果可知：在5～10 mm 的范围内，音圈电机的输出力为0.2～0.9 N之间；在6～8 mm 的范围内，音圈电机输出力的波动范围为0～0.3 N 之间。当缩比模型振动引起线圈位置变化时，输出力有一定程度的波动。缩比模型质量和刚度太小，波动的输出力相当于激励力，会对模态测试结果造成一定程度的影响。

4 结束语

本文以卫星环形天线为研究背景，基于悬吊装置设计方法，通过有限元计算和振动测试，研究了环形柔性结构悬吊装置的设计方法和固有频率，设计了1 套4 点悬吊装置，得出以下结论：1）在静力学分析时，悬吊装置是超静定的，需要补充变形协调条件使方程静定可解。2）有限元计算的结构静态变形与实际结构相比，存在一定误差。3）悬吊试验结果表明，悬吊电机的电压值和理论分析一致，第2 种假设更合理，也证明了静力学分析的合理性；同时，模态测试结果表明，悬吊前后的固有频率接近，“摇头”模态误差小，“点头”模态误差稍大，证明了悬吊装置的准确性。但受悬吊电机本身阻尼特性的影响，振动响应曲线衰减较快，需进行进一步的研究和优化。