基于改进A*算法的复杂停车场路径规划

邢孟阳，杜嘉豪，吴竟启，束 磊，郭中陽

（1上海工程技术大学 机械与汽车工程学院，上海 201620；2江苏超力电器有限公司，江苏 镇江 212321）

0 引 言

近年来，汽车保有量激增的同时，停车需求也急剧增长，为了满足停车需要，许多停车场都采用多层建筑结构，且建筑内部都十分复杂。在多层地下停车场中，由于缺少光线和标志物，驾驶员在其内部较易丢失方向感，这给停车和寻车均带来一定困难。为解决这个问题，研究学者做了大量的工作。李荣达等人采用图像识别和处理的方法，首先车载相机采集车辆周围环境图像，然后对图像进行透视处理，进而在不同灰度值下进行分割，提取出车位特征，最后通过霍夫变换提取出车位线，从而得到车位信息。该方法对于车载相机视觉范围内的车位信息具有良好的判别能力，为驾驶员提供了有效驾驶辅助。王雪松等人设计了一种改进的新型遗传算法，通过将相关领域知识融入到遗传的过程中，在不影响路径规划效率的同时，利用优化算子对算法进行优化，该方法能够有效提高利用遗传算法改进的路径规划效率。赵江等人在A算法基础上，引入了几何方法进行优化，其主要过程为：首先提取路径上所有的节点，然后删除其中的冗余节点以及可替换的拐点，最终将起点、必要拐点、终点连接成为一条最优路径，该方法有效缩短所规划路径的长度且减少了转向次数。华洪等人针对传统A算法局限于应用在静态环境下的全局中，在求解路径规划问题时存在搜索效率低，路径不平滑等问题进行了以下优化：对全局路径节点进行优化，对冗余节点要按规则进行删除，同时也可以按照规则新增必要节点，从而不仅使所规划的路径更加合理，而且还提高了搜索效率。Zhang等人提出一种结合Dijkstra和蚁群算法的融合算法，首先利用Dijkstra算法搜索效率高的特点，生成备选最优规划路径，然后利用蚁群算法具有信息反馈的优点，在备选路径中筛选出最优路径，该路径即为全局最优规划路径，最后设计实验方案，并通过数字仿真软件进行仿真测试，验证了该融合算法的优越性。

上述方法在解决特定问题时具有良好的表现，但也存在着不足，如文献［1］中提到的方法，其搜索范围局限于车辆周围，不能够实现全局搜索、全局规划。文献［2］中采用改进新型遗传算法，但该算法中起关键作用的适应度函数的选取难度较大，选取不当容易导致局部收敛，无法达到全局最优，且该算法参数较多，难以控制。因此本文选择对传统A算法进行改进优化，改进后的A算法不仅在搜索效率方面比其它算法更具优势，而且其所规划的路径对于驾驶员来说更加适宜，改进的算法控制简单，适合规模化推广应用。

1 A*算法原理

A算法是一种启发式搜索算法。在状态空间中，首先对每一个搜索的位置进行评估，得到最佳位置，然后从该位置再继续进行搜索，直至到达目标位置。算法实现流程图如图1所示。

图1 A*算法流程图Fig.1 Flow chart of A*algorithm

研究可得计算公式如下：

其中，（）是从初始位置经由节点（即现在所处位置）到达目标位置的估计距离；（）表示从初始状态到节点实际走过的距离；（）是从节点到目标位置的最佳路径的估计距离。

从式（1）中可以看出若要获取最佳路径，（）的选取十分关键。假设（）代表节点到达目标点的距离，那么（）与（）之间的关系可以表示如下：

（1）（）（）。此时，可以得到全局最佳路径，但这将导致搜索的节点过多，计算量过大，降低搜索效率。

（2）（）（）。即预估距离（）与实际距离（）相等，此时，算法的搜索过程将会严格按照最短距离进行搜索，这时拓展节点少，搜索效率相对较高，但路径未必是最佳。

（3）（）（）。此时，算法所需要搜索的节点少，提高了搜索效率，但容易导致算法局部收敛，从而无法得到全局最优路径规划。

2 对A*算法的优化

2.1 引入权重系数

A算法是在Dijkstra算法和BFS算法基础上，融合了二者的优点而成，由前文对算法的剖析可以了解，A算法中起最关键作用的是（），故当公式（1）中的（）值为0，此时A算法演变成为Dijkstra算法，而Dijkstra算法的优势就在于能够保证找到全局最短的路径，但是却需要遍历所有节点，故而会降低搜索效率。当公式中的（）要比（）大得多时，A算法中就相当于只有（）在起作用，此刻A算法就演变成为BFS算法，这个时候算法将严格按照拓展节点最短距离进行搜索，如此就能够保证得到一条相对最佳路径，但未必是最优路径。综上，是在传统A算法中引入权重系数（），原算法公式中的（）变成（）（），这里的（）≥1，由此得到改进后的算法用公式可表示为：

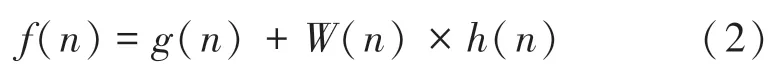
（）的引入可以为（）带来更大的权重，通过合理设置（）的值，使算法能够兼顾搜索效率和路径长度。

2.2 拐角优化

拐角优化示意如图2所示。图2中，绿色和黄色小点分别代表起点和终点，由起点至终点有图2中的1和2两种最短路径，对于算法而言，这2种路径在长度上并无差别，但考虑现实场景，对比1和2两种路径就会发现，路径1要比路径2多一次转向，而过多转向会给驾驶人带来不良体验，因此在路径规划中应予以避免。

图2 拐角优化示意图Fig.2 Corner optimization schematic diagram

3 模型的构建

为了更加真实还原停车场环境，研究中基于数字仿真软件测试平台构建了一个如图3所示的40×40的复杂停车场栅格地图。图3中，黑色的方格代表车位，考虑到在停车场中，车位的大小是基本一致的，故可用统一的变量来表示，停车场内部的道路是围绕着车位进行规划的，因此可以用车位间隙来表示道路。由于A算法是通过先计算初始位置与节点间的实际距离和节点到目标位置的估计距离，然后进行比较排序来实现拓展和路径规划的，因此就可以将每次拓展的代价设定为统一量，这样在计算的时候能够减小运算量，提高算法搜索效率。

4 仿真验证

本次仿真实验采用对比实验的方法，基于数字仿真软件测试平台，在相同条件下对传统A算法、改进A算法、Dijkstra算法、BFS算法进行对比实验。仿真实验结果如图3～图6所示。路径规划时间对比结果见表1，转弯次数统计结果见表2。

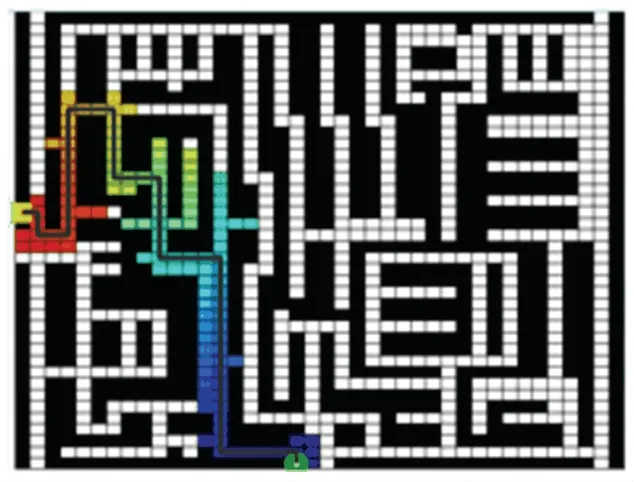
图3 传统A*算法Fig.3 Traditional A*algorithm

图4 改进A*算法Fig.4 Improved A*algorithm

图5 Dijkstra算法Fig.5 Dijkstra algorithm

图6 BFS算法Fig.6 BFS algorithm

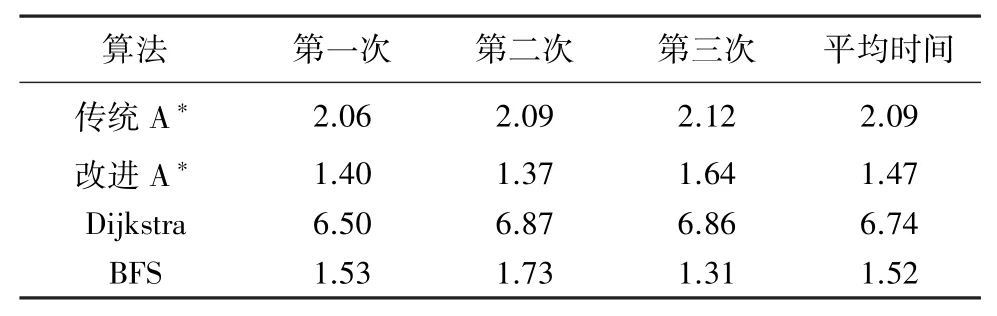
表1 路径规划时间对比表Tab.1 Comparison of routine planning time s

表2 转弯次数统计表Tab.2 Statistical table of turns

5 仿真结果分析

对比4种算法路径规划图，分析仿真实验结果可知，改进A算法的路径和传统A算法有明显区别，主要在于路径的平滑度，改进A算法要明显优于传统A算法，在路径长度方面，两者是相同的，这是由于初始位置和目标位置间的路径是固定的，因此改进A算法和传统A算法、以及BFS算法都搜索到了基于各自搜索规则所能达到的最短路径，而Dijkstra算法所规划的路径和其它3种算法都不相同，这是由于Dijkstra算法采用边缘拓展且向所有方向进行，拓展面积大，因此规划了一条最短的路径，但并不是最佳路径。从表1可以看出，改进A算法在搜索速度方便要比传统A算法和Dijkstra算法快，但比BFS算法要慢，究其原因分析可知，这是由于改进A算法要从全局考虑路径所造成的。从表2可知，路径规划中拐弯次数最少的是改进A算法，7次拐弯已经是所能达到的极限，这说明本次研究对算法的拐角优化发挥了作用。从实验结果分析，综合考虑路径平滑度、搜索时间、转弯次数三项关键指标，改进A算法与其它3种算法相比具有良好的优越性。

6 结束语

本文针对复杂停车环境中停车、寻车困难问题展开深入研究，选择对路径规划中比较成熟的A算法进行优化应用，传统的A算法是静态的规划，拓展节点相对较多，搜索效率相对较低，其规划出的路径相比启发式A算法而言存在不够平滑，不够人性化等缺点。因此本文通过引入权重系数，提高节点与目标点距离在算法中的权重来对算法进行改进。在实验测试中，研究发现算法在路径规划中可能会在相同距离条件下规划出多次转向路径，会给实际使用过程带来不良体验，因此通过在算法程序中加入拐角修正，使算法规划出的路径更加平滑，更加人性化，这些优化能够给实际使用者带来舒适的体验。未来还需解决在路径规划中全局规划、全局控制的问题，如需要将路径规划与车辆自主导航控制相结合，如此一来所规划的路径需要更加精细化，同时还要考虑到停车场内可能出现的会车、错车、行人、拥堵等复杂状况，及时引导车辆，避免危险发生。