基于液晶空间光调制器的计算全息波前编码方法

隋晓萌，何泽浩，曹良才，金国藩

（清华大学 精密测试技术及仪器国家重点实验室，精密仪器系，北京100084）

1 引 言

现阶段以平板显示为主的显示技术主要受限于显示器件与显示观感。在显示器件方面，LED 与液晶面板等应用广泛，但其发展受元件加工技术瓶颈的影响，限制了显示分辨率与视场角的进一步提升。在显示观感方面，基于双目视差的显示方案占据主流市场，但其无法提供真实三维观感的聚焦离焦效果，并在长时间观看后容易带来视觉疲劳。现有前沿显示技术研究以突破显示器件参数与显示观感的上限为主要目标，其技术路径可分为近眼显示与裸眼显示两类。近眼显示研究面向可穿戴显示设备的市场需求，采用视差屏幕、视网膜投影等技术，现已陆续产生融合虚拟现实（VR）、增强现实（AR）与混合现实（MR）等概念的高级显示设备［1］。裸眼显示研究面向大场景沉浸式的显示用户需求，已产生激光投影、全景LED 显示等技术方案，并成功用于北京冬奥会等超清显示场景。两种技术路径均以实现具有超高数据量、真实观感的三维显示为终极目标［2］。

传统的光学全息（Holography）技术包括记录和重建两个过程［3］。记录过程利用光的干涉原理，将相干光扩束准直为平面波前并分束为物光与参考光，物光照射物体并记录复振幅，参考光与物光发生干涉。物光波的振幅和相位携带着物体表面特征的相关信息，物光和参考光干涉产生的条纹则包含了物光波的振幅和相位并被记录在感光材料上。重建过程利用光的衍射原理，使相干平面波照射感光材料，在特定的衍射深度重建出被记录物体的振幅与相位。包含记录与重建的光学全息在提出时便引起广泛关注，在国防军工、文化娱乐、工业生产等领域均有着广泛的应用前景［4］。随着计算机技术与数字化编码器件的发展，传统全息中的干涉记录过程可以在计算机中通过数值计算实现，即计算全息技术（Computer-generated Holography，CGH）［5-7］。计算全息继承了传统光学全息技术中衍射重建真三维复振幅波前的优势，并将繁琐的全息光学实验操作转变为波前计算、波前编码与波前重建3 个过程。波前计算即通过矩阵计算的方法实现物光波的数值化波前传播，得到该复振幅波前在全息图平面的数学描述。波前编码将全息图平面的复振幅分布编码为与显示媒介数值格式相匹配的计算全息图。波前重建即计算全息图的光学重建过程，全息图被加载至波前调制器件［8-9］，通过相干光照射与衍射传播重建出物光波前。计算全息使用计算机来模拟光学的全息记录过程，极大地简化了全息图的生成步骤。同时计算全息技术使得全息三维重建摆脱了记录介质的限制，使全息图的数字化记录、编码与传播成为可能。计算全息技术的产生为诸多传统光学领域注入了新的活力，如计算全息的光镊阵列［10-11］可以实现动态并行的光学操纵，基于计算全息设计的衍射光学元件［12］能够实现更为精准灵活的光束整形，计算全息与光子晶体结合能够实现海量数据的光学存储与加密［13］。同时，计算全息也推动了前沿光学领域的研究，产生了很多新兴方向，如超表面全息［14-15］、计算全息激光加工［16］、计算全息光场调控［17］等。

近年来，以空间光调制器为代表的动态光学编码器件发展迅速，由此产生了数字化器件实时调制的动态重建物光波模式。现有空间光调制器根据调制方式可以分为振幅型与相位型两类。振幅型空间光调制器通过改变振幅透过率函数调制入射光的振幅，如数字微镜器件（Digital Micromirror Device，DMD）通过高速数字式反射光开关阵列的时域响应形成多样的振幅积分。相位型空间光调制器通过改变光程差调制入射光的相位，如硅基液晶（Liquid Crystal on Silicon，LCoS）通过液晶分子旋向调整有效折射率控制光程差［18］。为使全息图数据格式能够与编码器件相匹配，物光波在全息图平面的复振幅分布需要转换为相应的振幅型全息图或相位型全息图。

振幅型全息图的波前编码通过计算机模拟光学全息的干涉记录过程，将编码物光波的干涉场转换为振幅透过率函数。由于以DMD为代表的振幅型空间光调制器具有较高的刷新频率（～10 kHz），振幅型全息图也因此具有较高的时间带宽，并允许在光学重建中牺牲部分时间带宽从而实现扩展视场角［19］、抑制散斑［20］、引入运动视差［21］等效果。但由于振幅型全息图在重建时参考光照明的全息图为实函数，由全息图衍射生成的图像上方会出现未聚焦的共轭像引起的噪声。为解决共轭像问题，振幅型全息图的波前编码与光学重建过程需要引入倾斜角度的物光照明［22］或单边滤波［23-24］，从而分离或消除共轭像。

相位型全息图的波前编码是通过计算机模拟物光波衍射过程，将携带物体振幅信息的衍射场转化为具有均匀强度分布的全息图函数。以LCoS 为代表的大多相位型空间光调制器具有相对较低的刷新速率（～10 Hz），限制了相位型全息图的动态效果与功能扩展。但相位型全息图不受共轭像噪声影响，重建光能利用率高，因而也成为全息显示不可忽视的技术方向。由于全息图振幅项均匀化，自然物体的相位型全息图低频成分受到抑制，重建时的图像损失背景成分。为解决低频成分的缺失问题，相位型全息的编码需引入随机物体相位或优化过程［25-27］。同时，由于复振幅全息图可以通过一定的近似数学变换转化为相位型全息图，复振幅编码的全息图也可以通过相位型空间光调制器重建［28］。其中较为广泛应用的此类复振幅编码与转换方法包括双相位分解、误差扩散等。

本文从基于液晶空间光调制器的全息图编码算法出发，从优化求解相位型全息图方法与复振幅全息图转换编码方法两个方面对波前编码原理进行分类，对其数学理论与研究进展进行概述，并对计算全息波前编码方法的发展趋势进行展望。

2 优化求解相位型全息图方法

2.1 相位型全息图的计算原理

相位型全息图求解的基本问题可以描述为找到符合约束条件的全息图函数H=Aeiϕ，如图1 所示，该函数经由衍射传播能够得到物函数h=aeiφ.全息图函数的求解应满足3个基本约束［29］：

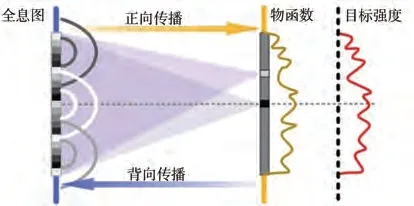
图1 相位型全息图计算原理Fig.1 Principle of computation for phase-type holograms

(i)a2=Iobj， （1）

(ii)ΔH＜∞， （2）

(iii)A2=|E|， （3）

其中，条件（i）代表物体平面的强度约束，即全息图重建强度等于目标物体强度；条件（ii）代表全息图带宽约束，即全息图具有有限的带宽分布；条件（iii）代表全息图自身的强度约束，即相位型全息图具有均一强度分布。由此可得，在全息图平面与物平面之间仅有物体相位φ为浮动变量，相位型全息图的求解可以转变为计算能够满足约束条件的相位φ。

相位型全息图的编码能够通过直接定义物体相位实现。1969 年，Lesem 等人提出了相息图（Kinoform）［5］，使用随机相位作为物体相位φ模拟光学散射，同时增强物体低频成分的扩散。但在光学重建中，随机相位引入散斑噪声，降低重建质量。1996 年，Aagedal 等人提出使用特定二次球面相位作为物体相位从而使物光在传播中汇聚并在全息图平面满足带宽约束［30］，但在重建中二次相位在图像周围造成伪影，也为全息图的高质量重建带来一定干扰。

为解决直接定义物体相位引起的重建噪声，优化算法被引入相位型全息图的计算中。由于全息图重建复振幅与重建强度之间的病态关系，存在多个有限带宽的相位型全息图其重建强度近似等于目标物体强度，因此全息图的求解可以通过非凸优化实现。全息图优化算法将相位型全息图的计算过程转换为逆问题求解，依据全息图的约束条件与物体相位的浮动，优化得到该问题的一个局部最优解。目前较为广泛应用的计算全息优化算法可以分为交替投影算法与非线性最小化算法。

2.2 相位型全息图优化：交替投影算法

交替投影算法（Alternating Projection Iteration Algorithm）通过在不同约束构成的集合之间投影迭代来更新求解的全息图函数。1972年，Gerchberg和Saxton 提出一种基于正逆傅里叶变换的交替投影算法［31］，简称为G-S 算法（图2）。该算法将物函数置于空域，将全息图置于频域，算法在迭代过程中分别在空域与频域施加相关约束条件。如图2 所示，迭代投影由空域开始，分别输入目标振幅与定义相位作为起始物函数；随后对该物函数进行傅里叶变换得到其频域复振幅分布，对该复振幅分布施加全息图带宽约束（ii）与强度约束（iii），并以约束后的复振幅分布作为全息图；将全息图进行逆傅里叶变换，从而得到新的重建物函数并对其施加物平面强度约束（i）使目标振幅替代重建振幅，完成一次循环。

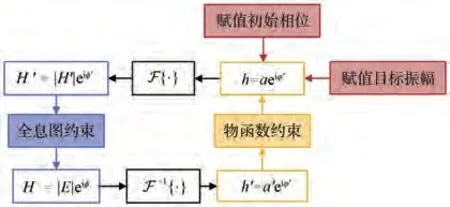
图2 G-S 迭代算法Fig.2 Principle of G-S algorithm

G-S 算法构成了计算全息交替投影算法的基本框架，其运算操作简单，因而在其原理之上产生了许多修正与改进算法。1978 年，Fienup 等人基于G-S 的交替投影框架提出误差下降算法（图3）［32］。误差下降算法在空域引入反馈约束机制：

图3 误差下降算法Fig. 3 Error-reduction algorithm

其中C代表满足约束的物点集合，ρ为反馈系数。

误差下降算法针对重建物函数中不同物点采取不同约束条件，能够有效提升重建图像质量并加快迭代收敛。

受误差下降算法思路影响，后续迭代算法产生了一系列在优化过程中使用与输出值相关的反馈约束或使用随迭代次数发生变化的软约束条件的方法［33］。其中，Wyrowski 等人提出在迭代中引入物函数平面的条件约束与全息图平面的软约束结合来使全息图函数平缓过渡至满足约束条件的局部最优解［34］。该算法在物函数平面预留信号区域与冗余区域，使用条件约束限定物函数的振幅替换区域：

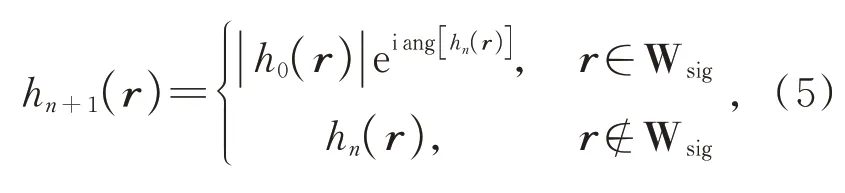
其中，ang[ ]· 为取相位算符，Wsig为信号窗内的物点集合。条件约束的使用允许物函数中的冗余区域来容纳重建噪声，实现信号区域的高质量重建。同时，在全息图平面引入随迭代次数变化的软约束：

Hn+1=ε|E|eiϕ+(1-ε)|H'|eiϕ， （6）

其中ε∈[0，1]为软约束系数，随迭代次数增加由0 渐变至1。

经由条件约束与软约束的配合，以及迭代中能量守恒系数γ对物函数平面与全息图平面能量关系的调控，混合约束的迭代傅里叶变换算法（图4）能够在实现较高精度的二维全息图重建。二次相位等缓变初始相位的引入也使该算法的二维强度重建日趋完善，逐步实现消除散斑、抑制伪影的效果［35-36］。

图4 混合约束的迭代傅里叶变换算法Fig.4 Principle of iterative Fourier transform algorithm with mix constraints

交替投影算法因其灵活性在三维物体的全息图运算中也有广泛的应用（图5）。三维交替投影的全息图优化算法可以分为相干叠加法、全局优化法与顺序优化法。

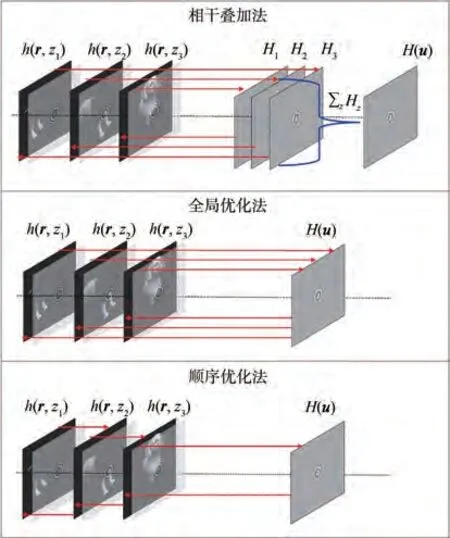
图5 交替投影算法优化三维物体全息图Fig.5 Optimization of holograms for 3D objects using alternative projection iteration algorithms

相干叠加法在不同深度的物体层与其对应的全息图平面之间交替优化，将优化后每一层物体的全息图平面相干叠加并取出其相位分量［30］。相干叠加法能够通过分层优化使物体满足带宽约束（ii），但强度约束（iii）会随叠加发生改变。叠加类算法能够最大程度保留物体深度信息，完整重建每一层物体的聚焦与离焦效果，适用于全息显示。

全局优化法则将不同深度衍射波前的相干叠加操作嵌套在单次迭代优化过程中［37］，并在全息图平面施加严格的带宽约束（ii）与强度约束（iii）。全局优化算法中三维物体的零强度点与非零强度点共同组成物体的强度约束（i），因此该方法优化所得的相位型全息图无法在聚焦深度处保留其余深度的离焦图像，其重建效果与真实世界的观感相悖。全局优化法由于能够重建单一深度振幅信息并打破层间串扰，在光学存储与加密［38］、光遗传技术［39］等领域有着广泛应用。

顺序优化法将分层的三维物体沿深度依序完成衍射计算，由前一层优化相位与约束强度得到计算层的复振幅［40］。顺序优化法在深度表现上与全局优化法类似，强度零点构成暗像素阻挡其他层光线的传播。但由于全息图按深度顺序传播，远离全息图的物体层受靠近全息图的物体层重建误差影响，重建图像质量下降。因此在顺序优化法的重建结果中，距离全息图最近的物体强度具有较高的重建精度。

2.3 相位型全息图优化：非线性最小化算法

非线性最小化算法由Zhang 等人于2017 年引入计算全息领域［41］，如图6 所示，其优化原理为定义求解相位型全息图逆问题的损失函数，通过求解损失函数对于全息图的导数，搜索损失函数梯度下降的方向并寻找相对应的全息图解。

图6 非线性最小化逆问题模型Fig.6 Inverse problem for nonlinear minimization

相位型全息图的求解可定义为优化问题：

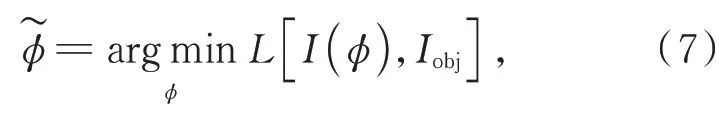
其中I为全息图重建强度，Iobj为物函数强度。非线性最小化算法的优越性表现在损失函数L的灵活选择。由于全息图重建存在目标值，l2范数能够使物函数满足强度约束（i），成为了较为广泛应用的损失函数之一，其表达式为：

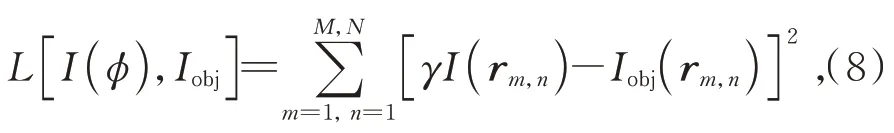
式中，γ为依据能量守恒控制全息图重建强度的系数，其表达式为

除l2范 数 外，0-1 损 失、SSIM 损 失 函 数 等 也对特定的物体强度具有突出的优化效果。在此以l2范数为例展示导数求解傅里叶全息图过程。

为搜索损失函数的梯度下降方向，依据链式法则求解损失函数对于全息图的导数，展开为：

展开式中第一项为l2范数对全息图重建强度的导数，求解为：

导数展开式第二项为全息图重建强度对全息图复振幅分布的导数，将全息图重建的传播过程转换为矩阵运算，即可得到：

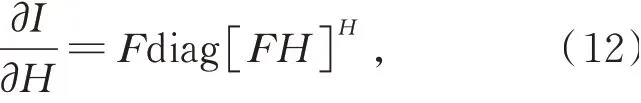
其中F代表傅里叶变换矩阵，[·]H为共轭转置算符。

导数展开式第三项为全息图复振幅分布对相位型全息图求导，根据欧拉公式展开复振幅表达式，可以得到该项为：

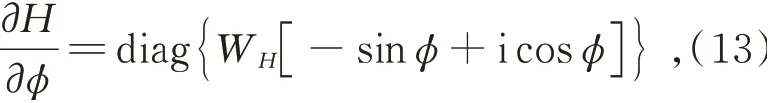
其中，WH为窗函数，它限制全息图的带宽并使全息图满足带宽约束条件（ii）。基于以上运算，结合梯度下降类型优化算法，即可实现在约束条件限制的集合内搜索全息图的局部最优解。较为广泛应用的算法包括准牛顿算法［42-43］、Wirtinger flow［44］、随机梯度下降［45］等。

非线性最小化类型算法与交替投影算法相比，运算时间较长，计算量较大。但其搜索过程中覆盖到的解函数范围略大于交替投影算法，因而在同等全息图参数与衍射重建模型下，非线性最小化算法时常能够得到重建准确度更高、噪声更低的结果。

2.4 相位型全息图优化：优化相位掩膜法

相位型全息图在物体平面与全息图平面之间仅有物体相位φ为浮动变量，由此Bräuer 等人于1991 年提出可以通过优化物体相位掩膜求解相位型全息图［29］。通过预先的相位掩膜优化使透过掩膜传播的物体窗函数近似满足全息图约束，随后将该相位掩膜作为物体相位分量计算得到全息图。优化后的相位掩膜能够使物体经过一步运算［46］或快速收敛迭代［47］得到具有较高重建精度的相位型全息图，在很大程度上缩减了全息图优化所耗的计算时长。

为使相位掩膜能够配合物体衍射产生具有较高重建质量的相位型全息图，掩膜优化算法（图7）通过设计不同的初始相位得到不同重建特性的全息图。使用随机相位作为初始优化得到的相位掩膜能够模拟物体散射表面［48］，具有符合自然物体表现的重建聚焦与离焦效果，适用于三维物体重建。但由于有限带宽的随机相位存在奇点与相位涡旋，其重建强度受散斑噪声影响。使用二次球面相位作为初始优化得到的相位掩膜能够避免散斑噪声［49］，产生较高的重建精度，但其相位缓变导致全息图编码容错率低，重建视场角受限，多用于二维图像的全息投影。

图7 相位掩膜优化算法原理Fig.7 Principle of optimized phase mask algorithm

3 复振幅转换编码方法

由于现有空间光调制器大多仅能调制振幅或相位，随之产生了将复振幅通过一定近似转换为相位或振幅型全息图的复振幅编码方法。其中复振幅-相位的转换方法因其转化误差低、运算效率高，在计算全息中应用较为广泛。

3.1 双相位全息图

双相位全息图（Double Phase Hologram）于1978 年提出，其编码方法是基于欧拉公式将归一化复振幅分量分解成为两个具有相同均匀振幅的分量［50］：

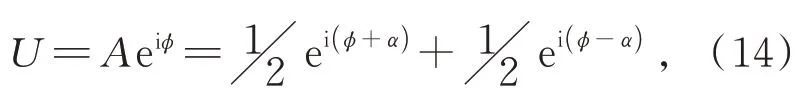
其 中α=cos-1A且。由 此 得 出，通过两幅相位型全息图的相干叠加，可恢复出全息图平面的复振幅场，如图8 所示。

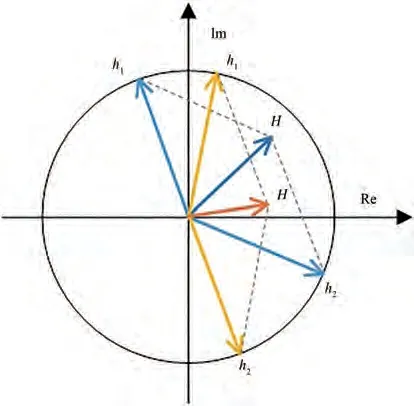
图8 均匀振幅圆内的复振幅分解原理Fig.8 Principle of complex modulation in the unite circle

基于双相位分解原理，演化出分解的双相位分量逐个像素穿插排列，使得相邻像素在衍射传播的过程中相干叠加的复振幅编码思路。

2002 年，Arrizón 与Sanchez-de-la-Llave 为在空间光调制器上实现横纵采样间隔一致的双相位全息图［51］，提出由4 个像素组成复振幅单元（图9（a）），即为巨像素编码方法（Macro Pixel Encoding）。在一个巨像素单元内双相位分量沿对角线交错排列，该结构既能够保持全息图对复振幅场的水平与竖直方向采样间隔相等，同时通过不同方向的错位补偿，极大地减小了双相位全息图的错位噪声。但由于该方法中一个复振幅的巨像素包含4 个空间光调制器像素，双相位编码对复振幅光场进行了降采样，空间带宽积的利用率仍旧相对较低。

图9 空间光调制器的双相位编码方式Fig.9 Double-phase encoding on the spatial light modulator

2014 年，Mendoza-Yero 等 人 提 出 了 一 种 基于单像素操作与采样的双相位编码方法［52］，被称为单像素编码方法（Single Pixel Encoding）。如图9 所示，将分解后的双相位分量通过互补的二元光栅进行像素级采样，该二元光栅分布为透过率0 或1 的像素棋盘格，采样后的双相位分量相加即为一幅相位型全息图。

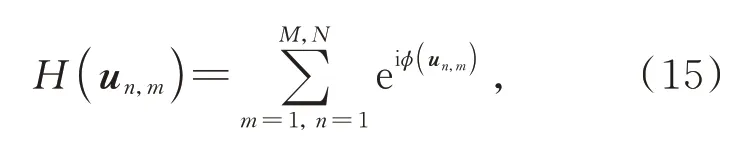
其中ϕ(un，m) 可表示为：

ϕ(un，m)=φ(un，m)+

( -1)n+mcos-1A(un，m) . （16）

图10 为基于二元光栅采样的单像素双相位编码方法的计算流程。编码后的双相位全息图像素排布如图9（b）所示，采样后的双相位分量交错分布。

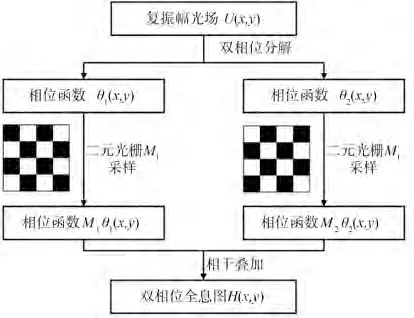
图10 单像素双相位图编码流程图［52］Fig.10 Encoding flow chart of the single-pixel doublephase hologram［52］

棋盘格采样的单像素方法保证了从物体到全息图的运算过程中采样点数始终一致，极大地降低了运算的复杂性，提升了运算效率，是保证双相位全息图能够应用于实时全息显示的关键性一步，成为目前最广为使用的编码方法。但由于该方法中运用了互补采样，由双相位恢复的复振幅受相邻像素近似的影响，局部重建精度略低于巨像素方法。

双相位全息图重建质量造成影响的主要因素，在于每个复振幅调制单元内的双相位分量存在空间错位，无法完全相干叠加［53-54］。由于双相位全息图噪声与信号在频域存在重叠，双相位全息图重建时需依靠空间滤波，遮挡大部分噪声。但同时由于包络函数分布特性，空间滤波也无法完全消除全部位移噪声，并部分损失图像重建细节。

虽然错位噪声存在，双相位全息图因其能够直接编码复振幅，与优化求解的相位型全息图相比具有明显较高的重建信噪比与运算效率，在全息显示上具有广泛深入的应用。

3.2 误差扩散方法

误差扩散方法（Error Diffusion Algorithm）最早使用于二值全息图编码，它将灰度图二值化导致的量化误差分散到周围像素，从而提升二值全息图的重建效果［55］。在相位型编码器件出现后，这种方法也被用于编码复振幅，将相位型全息图与所编码的复振幅分布之间的误差扩散到相邻像素中。

复振幅分布转化为相位型全息图的过程中会产生误差：

Eerr=Aeiϕ-eiϕ， （17）

如图11（b）所示，这项误差可以通过不同的传递系数k1，k2，k3，k4传递至相邻4 个像素，并更新周围像素值：

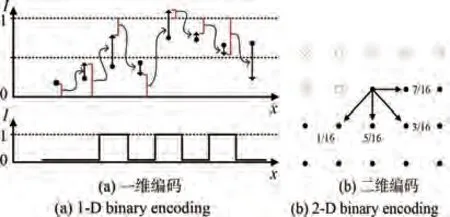
图11 误差扩散法编码二值化全息图［57］Fig. 11 Binary hologram encoding using error diffusion［57］

在此原理上，产生了多种针对误差传递系数与误差扩散方向的改进算法［56-57］。如2013 年，Tsang 与Poon 提出的双向项误差扩散算法（图12），分别沿两个不同的方向扩散误差并有效提升重建质量［58］。

图12 双向误差扩散方法［58］Fig.12 Bidirectional error diffusion method［58］

值得注意的是，误差扩散方法适用于编码相位变化平滑的复振幅分布，在计算相位变化剧烈的物体或随机相位物体时会产生较为明显的编码噪声，导致重建质量下降。此外，误差扩散方法在计算相邻像素时有着严格的先后关系，因此在运算时无法并行加速，全息图的运算量随采样点数的增加而增加。

4 总结与展望

本文介绍了以液晶空间光调制器为调制器件、以相位型全息图为调制函数格式的计算全息波前编码方法，包括逆问题优化求解的相位编码与正向近似转化的复振幅编码，分析了不同编码方案的优势与挑战。

计算全息的波前编码方式与调制器件的原理与参数紧密相关。随着大尺寸液晶空间光调制器与多种新型显示器件的发展，波前编码的方法与形式也日趋多样化。但波前编码算法也始终保持着相对恒定的侧重方向：

（1）高重建准确度。波前编码算法的重建强度准确性是计算全息波前编码所需要解决的基本问题。振幅编码的孪生像问题、相位编码的散斑与伪影问题、复振幅编码的转换误差问题是波前编码准确性提升所面临的重要难点。现有算法针对这些难点问题提出了部分解决思路与方案，但解决方案带来的带宽、视场角、空间分辨率方面的损失也为波前编码带来了新的挑战。

（2）高空间带宽积。相位编码与复振幅编码中均存在噪声与带宽的取舍问题。在高质量计算全息重建中，重建强度场的信噪比、空间分辨率、边缘锐度、对比度等都是对其视觉效果具有关键作用的指标，因此实现最大的空间带宽积利用率始终是波前编码算法追求的重要目标。

（3）高运算效率。相位剧烈变化物体的相位型编码与复振幅编码过程大多需要依赖优化算法，其运算耗时长，实时编码难度大。近年深度学习算法被引入计算全息领域，为全息图的快速生成提供了解决途径。但深度学习相关算法的全息图生成准确度与计算全息波前编码模型密切相关，编码算法的有效性仍是突破算法效率瓶颈的关键方向。

近年来计算全息在算法、器件与系统层面均取得了跨越式的发展，以优化算法与深度学习结合为主的相位编码方法在能量利用率与带宽率用率上具有突出表现，以双相位为主的复振幅编码方法兼备了高运算效率与高重建精度，使得实现高分辨率、大视场的真三维实时全息显示成为可能。以空间光调制器为代表的调制器件，不断突破像素数目、视场角、像素尺寸的上限，为下一代显示技术奠定了基础。同时，散射介质与超颖表面介入新一代显示系统刺激了波前编码技术的更新与迭代。针对不同的显示应用场景，采用不同的显示器件，设计适配的显示系统与运算算法将是未来全息显示的发展方向。