时变大气湍流对阵列合束激光传输特性的影响研究

李林野，邹 嵘，罗丽平，叶丹戈

（中国电子科技集团公司第二十九研究所，四川 成都 610036）

0 引言

大气湍流效应对激光传输的影响广泛体现在激光成像、激光测距、激光通信以及高能激光系统等工程应用领域，相关的学者也在大气湍流对激光传输的影响方面开展了相应的研究工作[1]。由于大气湍流对激光传输的影响的物理本质是湍流引起传播光束波前相位的随机起伏，所以从已有的研究成果可知，目前常用的研究手段大多为通过构建大气湍流相位屏模拟真实的大气湍流环境，并以激光经大气传输至接收端的光束质量作为湍流对激光传输影响效果的评价依据。对于阵列合束激光，国内外有学者通过仿真和试验手段对其在大气中传输时受湍流的影响进行了深入的分析研究[2]，比较全面地总结出了不同类型的合束激光在受到不同程度的大气湍流影响后传输至目标处的光束质量的变化情况。从上述研究可知，用于模拟大气湍流相位屏的方法大多是以功率谱反演（FFT）法[3]和Zernike 多项式法[4]为主，且模拟生成的湍流相位屏从空间上满足对应的功率谱模型。

大气湍流的统计特性决定了其相位不仅是空间的函数，同时也是时间的函数。因此，在研究激光尤其是连续激光经大气传输后的特性时，大气湍流的时变特性对于研究过程和结果显得尤为重要。因此，本文在进行非相干阵列合束激光的传输聚焦研究时，充分考虑了时变大气湍流对激光传输特性的影响，分别在不同的大气相干长度和风速条件下构建了随时间变化的大气湍流相位屏序列，并以激光经湍流相位屏序列传输至目标处的桶中功率比（Power In the Bucket，PIB）作为研究对象。

1 时变大气湍流模型研究

1.1 相位屏序列构造

常用的时变大气湍流相位屏序列的生成方法主要为湍流冻结法和样条插值法。湍流冻结法[13]基于泰勒湍流冻结假设理论。该理论认为，在一定的时间间隔内，大气湍流畸变波前的空间相对结构保持不变，在湍流介质中以横向风速v掠过光学孔径。因此可首先模拟生成一个较大尺度的相位屏（母屏），再根据横向风速v的大小连续选取母屏上的子区域作为子相位屏（子屏），最后将这些子屏构成时变相位屏序列。该方法虽然能模拟任意功率谱的大气湍流，但是模拟生成的母屏数据量很大，且低频成分不突出。为了提高计算效率，本文选择使用样条差值法构造相位屏序列。

样条插值法[5]在使用Zernike 多项式法构建静态的大气湍流相位屏的基础上引入了时间变量。Zernike 多项式法可将大气湍流的静态相位表示为如下形式：

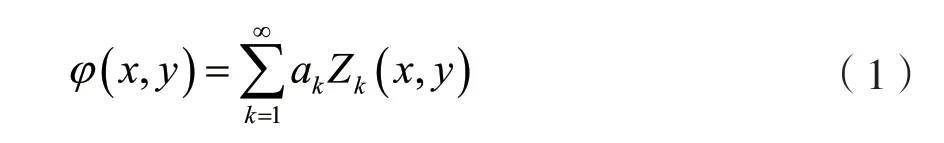
若式（1）中第k阶多项式系数ak为满足某种规律的时间变量，即可实现生成时变大气湍流相位屏序列。因此，可在t=0 时刻，先利用式（1）生成初始静态相位，然后当t＞0 时，静态相位的任意阶系数随时间变化，且变化过程满足一定的规律，即可实现对时变大气湍流相位屏序列的模拟，因此可令该序列表示为[6]：

本文选取最常见的满足Kolmogrov 谱分布的大气湍流进行分析，根据Tatarski's 模型理论[7]，该谱对应的相位屏序列在时域上的相位方差具有高斯随机分布的特性，所以式（2）中第k阶多项式里的时变系数Xk可视为时间序列上的高斯随机噪声，其服从均值为0、方差为某一特定值的高斯分布。若只考虑式（2）中的时变状态，则令：

式（2）可改写为：

NOLL 定义了湍流相位的均方残差，其表达式可写为：

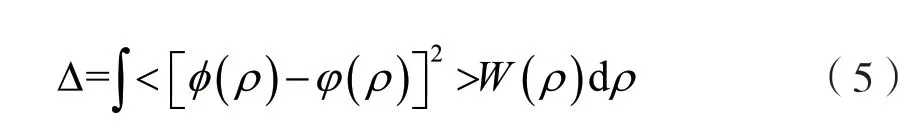
式中：ρ为在对应的相位分布圆域内的归一化的极坐标径向变量，W(ρ)为单位圆内的光瞳函数。

φ(ρ)为时变湍流相位的理论值，φ(ρ)为时变湍流相位的拟合值，即为式（4），<*>为系综平均。根据大气湍流的统计理论，由于湍流相位屏在系综域上也满足高斯分布，所以在后续推导中将时间平均等同于系统平均考虑。

同时，若选择使用前K项Zernike 多项式进行相位屏拟合，则式（5）经过推导后可简化为如下形式：

FRIED 经过计算归纳得到了均方残差ΔK的取值规律[8]如表1 所示。表1 中，D为光学孔径，r0为大气相干长度。

将表1 中的计算结果代入式（6）进行递推计算后，可得到表2 所示的计算结果。

表1 ΔK 计算结果

表2 计算结果

由上述计算结果可知，只要确定了光学孔径D和大气相干长度r0，即可确定每一个多项式系数bk平方的系综平均，而ak为已知参数，所以由式（4）可计算每一个多项式对应的Xk在时间序列上的方差，最终可得到每一个Xk随时间t变化的序列，同时将序列进行3 次样条插值即得到连续变化的曲线，它表征了大气湍流相位屏对应的不同的Zernike项随时间变化的趋势。

令光学孔径D=400 mm，在对应激光波长λ=1 080 nm 条件下的大气相干长度r0=10 cm。图1 为从经过样条插值后的大气湍流相位屏序列中任意抽出的连续变化的9 幅相位屏图像。

从图1 可以看出，利用插值法得到的连续变化的大气湍流相位屏的变换过程较为平滑，可以更真实地模拟大气湍流在时域上的变化状态。

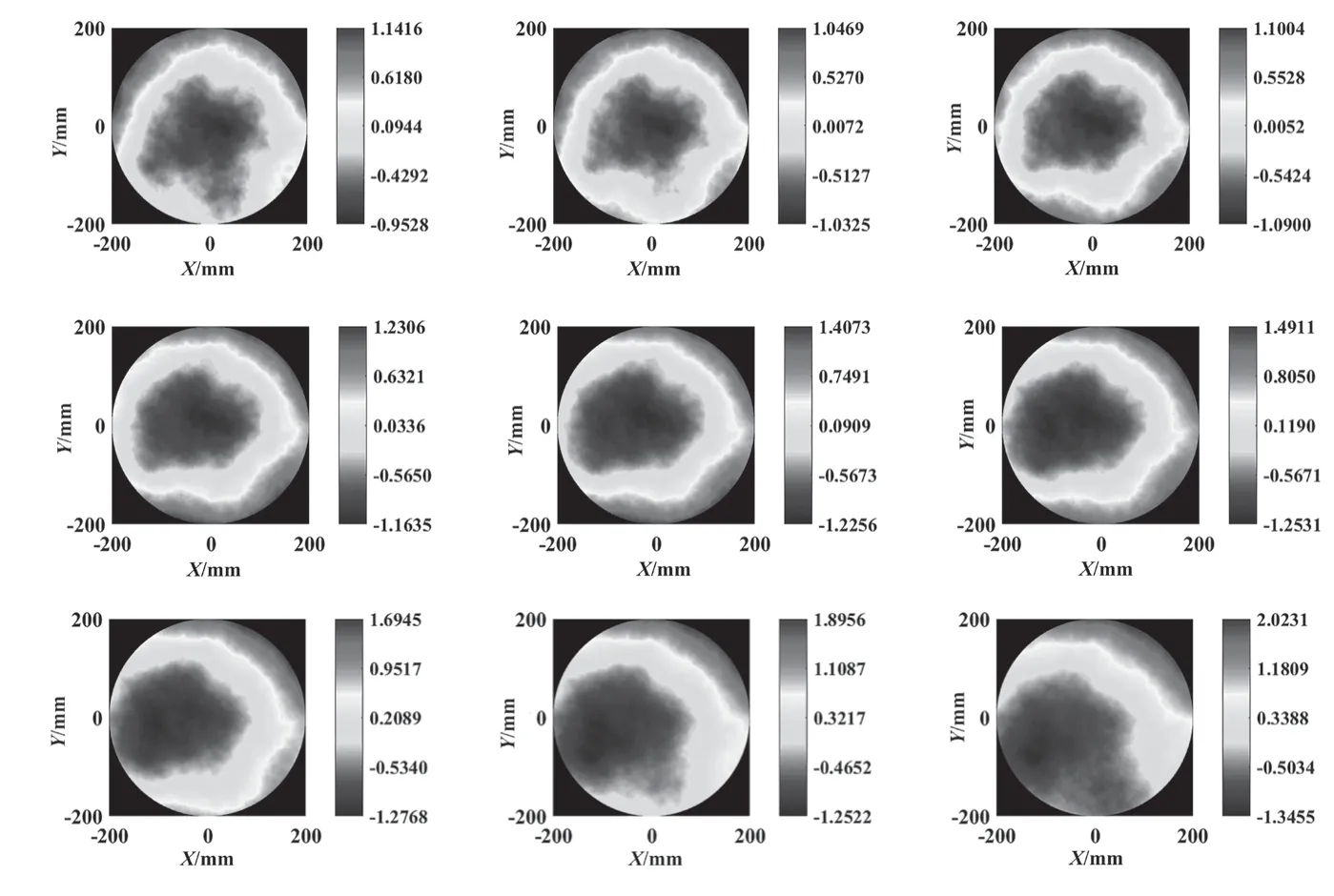
图1 连续变化的大气湍流相位屏（从左到右，从上到下）

1.2 大气湍流相位屏序列数与时间长度的关系

对于能量型的激光应用系统，在研究大气对激光传输特性的影响时，一般关心激光传输至目标处的远场光束质量，在这个过程中，同时考虑时间的累积效应会对研究更有意义，因此本节将研究把相位屏序列数与时间长度进行关联。根据泰勒湍流冻结假设理论[9]，可以假设时长t为平均风速为v时大气湍流畸变波前完全掠过口径为D的光学孔径所需的时间。因此，经过时间t后，光学孔径D对应的湍流波前可以用另一个同样满足Kolmogorov湍流统计特性的随机波前来表示，且t的表达式为：

同时，与空域尺度上的大气相干长度r0对应，时域尺度上的大气相干时间τ0也是另外一个重要的大气参数，它表示通过大气到达系统波前的时间相关性，不同时刻到达观测点的波前，如果时间间隔超过τ0，就认为它们之间的相位扰动不再相关，其表达式为：

根据对τ0的定义可知，满足Kolmogorov 统计特性的大气湍流在经过时间τ0后不再满足该统计特性。因此，为了保持每一帧大气湍流相位屏的Kolmogorov 统计特性不被破坏，就需要在t内对每一个τ0点间隔进行插值以更真实准确地模拟大气湍流的时域变化。需要插值的帧数N可表示为：

根据式（8）～式（10）可知，若需要研究的时间长度为T，则对应未插值的大气湍流相位屏序列数目可表示为：

每个相位屏之间应进行插值的数量最少为N-1。

2 时变大气湍流对激光传输特性影响仿真

2.1 激光传输建模

以非相干阵列合成形式的激光系统为例，激光经过调焦状态的发射望远镜系统扩束后传输聚焦至L处的传输过程可等效为激光先经过无焦状态的扩束望远镜系统，然后再经过焦距为L的单透镜聚焦。因此，根据角谱衍射理论，可计算得到激光在真空条件下传输距离为L时的复振幅分布，而大气湍流相位屏则用于对复振幅的相位部分进行调制。

对于表征时变状态的大气湍流相位屏序列，可先用序列中每一个相位屏对激光的初始复振幅的相位部分进行调制，同时得到每一个传输后的激光复振幅，最后再将所有传输后的激光复振幅进行相加即可模拟得到受时变大气湍流影响后的激光光强分布。

令单束激光为基模高斯光束，经过发射望远镜系统后的主要参数如表3 所示。

表3 激光参数

结合表3 的参数，根据激光传输模型仿真计算后可得激光在真空中传输前后的光强分布如图2所示。

图2 激光光强分布图

2.2 不同大气相干长度对激光传输特性的影响

从1.2 节可知，使用插值法模拟生成大气湍流相位屏序列时，若阵列激光的光学孔径D、激光传输时长T确定，则大气相干长度r0与风速v会影响生成的相位屏序列数量，最终会影响阵列合束激光经大气传输后的光束质量。

假设阵列激光的光学孔径D=400 mm，激光作用时长T=1 s，且传输的环境中风速v=3 m·s-1，分别取大气相干长度为5 cm、10 cm、20 cm 和40 cm，根据上述参数以及式（8）～式（11）可计算得到不同大气相干长度对应得到的不同数量的大气湍流相位屏序列，同时将其代入激光传输模型中进行仿真计算，可得到非相干合成形式的阵列激光传输聚焦至1 km 处远场时的聚焦光斑分布及桶中功率比，如图3 所示。

图3 不同大气相干长度下的激光远场光强分布图

计算桶中功率比所需的环围圆是以非相干合成形式的阵列激光在自由空间中传输聚焦至l=1 km处时光斑占总功率86.5%范围对应的圆域，其直径经计算为D=60.3 mm，如图2（b）所示。仿真结果如图3 所示，数据统计表如表4 所示。

由图3 和表4 可知，在相同的作用时间内，若其他因素不变，则随着大气相干长度增大，即湍流强度减弱，合束激光远场光斑直径会变小，桶中功率比会增大，且逐渐接近理想值。

表4 不同大气相干长度下激光远场参数

2.3 不同风速对激光传输特性的影响

在相同的光学孔径、大气湍流条件和激光作用时长条件下，设置不同的风速参数进行仿真，可得到当风速为1～8 m·s-1时对应的激光远场桶中功率比。在每一个相同的大气湍流条件下，当光学孔径D=400 mm，激光作用时长均T=1 s 时，不同风速条件下对应的非相干合成形式的阵列激光传输聚焦至1 km 处远场时的桶中功率比计算结果如图4 所示。

图4 不同风速下的桶中功率比

由图4 可知，在相同的大气湍流条件下，若激光传输时长也不变，则随着平均风速的增大，合束激光传输至远场的桶中功率比会降低，即光束质量下降。

3 实验验证

使用非相干阵列合束激光系统样机在外场开展距离为1 km 的传输聚焦实验，实验布局如图5 所示。

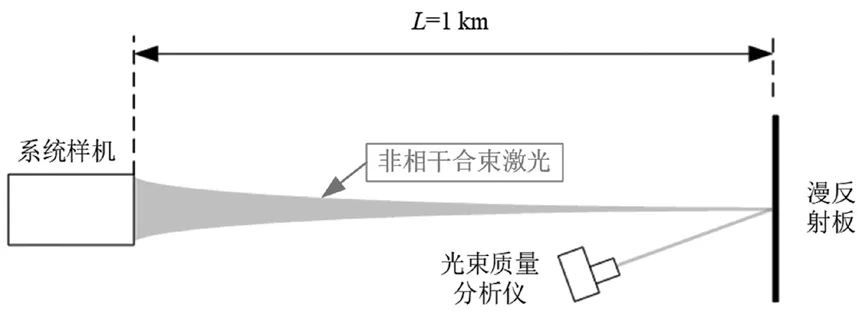
图5 外场实验布局图

实验选用Spiricon 公司的光束质量分析仪，按照图5 的布局放置好后，对光束质量分析仪进行背景滤除，再设置积分时间为1 s，最后进行物象比标定，得到比例系数k=39。通过大气参数监测系统实时监测激光传输路径上的大气相干长度，当r0=20 cm，风速v=3 m·s-1时，系统样机持续发射激光大于1 s。在激光发射结束后，读取光束质量分析仪上的测试结果，如图6 所示。

图6 1 km 处光斑测量结果

根据光束质量分析仪的物象比k以及图9 中光斑测量值结果可以得到上述实验距离下光斑直径的实际值。该值与相同聚焦距离下的光斑直径仿真值（图3（c））非常接近。而由于桶中功率比与光斑直径相关，因此激光桶中功率比的实际值与仿真值也非常接近，各值的具体参数如表5 所示。

表5 光斑直径参数

4 结语

本文通过构建时变大气湍流相位屏序列，模拟了真实条件下大气湍流随时间的变化过程，并以非相干阵列合束激光经大气传输后的远场光斑桶中功率比为研究对象，分别在不同的大气相干长度和不同的风速条件下进行了仿真计算。从计算结果可知，在相同的激光作用时间内，合束激光远场光斑的桶中功率比会随大气相干长度的增大而增大，因为大气相干长度越大，大气湍流效应越弱，传输激光受到大气的影响就会更小，所以远场光束质量会更好；而在相同的激光作用时间和相同的大气相干长度条件下，合束激光远场光斑的桶中功率比会随风速的增大而减小，因为风速越大，大气湍流波前畸变分布的变化频率越快，则在相同的作用时间内，传输激光就会受到更多不同的湍流波前畸变调制，最终的远场光束质量会更差。同时，开展了外场验证实验，实验结果表明在大气相干长度r0=20 cm，风速v=3 m·s-1的大气条件下，非相干阵列合束激光传输聚焦至1 km 时的光斑直径和桶中功率比与仿真结果基本一致。因此，实验结果证实了仿真过程的正确性。综上所述，本文对大气湍流的研究与实际情况更加吻合，可为改善能量型的激光应用系统在激光传输过程中受大气的影响提供更全面的参考。