1961～2020年三江源地区候降水变化特征分析

张 青，陈 丹，唐忠涛，白延晖，祁栋林

(1.青海省玉树藏族自治州气象局，青海 结古 815000；2.青海省玉树藏族自治州杂多县气象局，青海 萨呼腾 815300；3.青海省防灾减灾重点实验室，青海 西宁 810001；4.青海省气象科学研究所，青海 西宁 810001)

降水作为水循环过程的重要环节之一，是气候变化研究的主要对象，降水变化的研究对农作物生长情况、植被恢复状况、水资源利用及管理具有重要意义。中国区域的降水以年代际变化为主，西北西部的降水从上世纪80年代中开始明显增多，青藏高原地区属于季风降雨区，在东亚季风、印度季风、高原季风和西风带系统的共同影响下，降水的局部特征显著，20世纪70年代到90年代初期降水变化不大，90年代中后期开始明显增加，并且青藏高原降水区域性分布明显，受地理因素影响较强[1～4]。青藏高原三江源地区素有“江河源”、“中华水塔”、“亚洲水塔”之称，是亚洲、北半球乃至全球气候变化的敏感区，也是中国乃至世界生态安全屏障极为重要的组成部分，具有不可替代的生态战略地位[5]。

以往的研究大多采用月降水量、季降水量、年降水量来分析降水季节性特征以及影响因素的关系，在一定程度上反映出较大区域内降水的基本气候状态和长期变化特点，但在反映较小功能区或局部区域的变化特征研究上还是不够具体和细致[6～8]；虽然李晓英等[9]利用近50 a青藏高原69个气象台站降水资料，得到近50 a来青藏高原降水量总体呈现增加趋势，并且得到青藏高原降水由东南向西北递减；黄露等[10]利用ERA-Interim再分析资料，计算了1979～2015年青藏高原上空大气可降水量，并分层分析了其空间分布、气候倾向率及年际和年内变化特征；校瑞香等[11]利用青海43个气象站的降水和水汽压资料，计算了不同功能区的大气可降水量和降水转化率，得到可降水量自西向东呈逐渐增加趋势，降水转化率形成以青海湖区为中心的马鞍型场。

目前对三江源地区气候研究主要在气候和生态方面的研究，三江源地区在过去60 a增温显著并且增暖速率是全球平均水平(0.16℃/10a)的2倍以上，同时大幅高于同纬度及中国区域，在全球变暖背景下，三江源地区大部分极端气候指标上升[12]。李林等[13]早期研究表明三江源地区在21世纪前表现为气温升高、降水减少和蒸发增大出现干旱化气候变化趋势，在气候干旱化和人为活动的影响下出现了草场退化、湖泊萎缩、河流流量减少、土壤沙化和水土流失等生态环境荒漠化问题。从三江源地区雨季水汽输送特征来看[14]主要水汽输入边界的水汽通量1965～2004年来呈现减少趋势，影响三江源地区21世纪前的降水量，对生态恢复不利。进入21世纪后少有对三江源地区降水的变化研究分析，随着国家生态战略的布局、青海生态文明大省的建设、人工影响天气的布局，三江源地区生态恢复改观显著，本文就三江源地区着重分析候尺度上降水量的变化特征，为三江源生态恢复建设工程提供技术依据和数据支撑。

1 研究区概况

青藏高原为亚洲内陆高原，是中国最大、世界海拔最高的高原，被称为“世界屋脊”、“第三极”。三江源地区是青藏高原的腹地和主体，可可西里山及唐古拉山脉横贯其间，海拔为3335～6564 m，地理位置为北纬31°39′～36°12′，东经89°45′～102°23′，总面积为30.25×104km2，约占青海省总面积的43%，高大山脉的雪线以上分布有终年不化的积雪，雪山冰川广布，是中国雪山、冰川集中分布地之一(图1)。河流密布，湖泊、沼泽众多，是世界上海拔最高、面积最大、湿地类型最丰富的地区。也是长江、黄河和澜沧江的源头汇水区，面积按流域分为：黄河源区面积16.7×104km2，占三江源地区总面积的46%；长江源区面积15.9×104km2，占44%；澜沧江源区面积3.7×104km2，占10%。长江总水量的25%，黄河总水量的49%和澜沧江总水量的15%都来自于三江源地区，使这里成为我国乃至亚洲的重要水源地，素有“江河源”、“中华水塔”、“亚洲水塔”之称。区内气候属青藏高原气候系统，为典型的高原大陆性气候，在自然地理上占有非常重要的地位。

图1 三江源地区高程及气象站点分布图

2 资料与方法

2.1 资料

本文选取了三江源地区兴海、同德、泽库、杂多、囊谦、曲麻莱、玉树、清水河、玛多、大武、达日、久治、五道梁和沱沱河等14个气象观测站，1961～2020年逐日降水量数据。1981～2010年为历史气候。

2.2 方法

2.2.1 线性倾向估计 用xi表示样本量为n的某一气候变量，用ti表示xi所对应的时间，建立xi与ti之间的一元线性回归方程：

(1)

方程(1)可以看做一种特殊的、最简单的线性回归形式。它的含义是用一条合理的直线表示x与其时间t之间的关系。方程中a为常数，b为回归系数。a和b可以用最小二乘法进行估计。

(2)

其中

将n个时刻的累积距平值全部算出，即可绘出累积距平曲线进行趋势分析。

2.2.3 变异系数 变异系数反映数据离散程度，当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响。

变异系数 C·V=(标准偏差SD / 平均值Mean)×100%

变异系数小于15%，表示数据波动稳定，属低变异，变异系数在15%～80%之间为中等变异，大于80%为高变异。

3 结果分析

3.1 候降水量的气候状态

三江源地区1961～2020年候平均降水量总体呈正态分布(图2)。候平均降水量最大出现在38候(20.19mm)，约占全年4.3%，候平均降水量最小出现在68候(0.22mm)约占全年0.05%；62候至次年12候(除10候外)候平均降水量基本低于1.0 mm，降水较少且气候干燥；13候至61候候平均降水量≥1.0 mm，其中降水集中分布在30候至53候(跨越候数为24候，期间降水约占全年75.9%，各候降水量≥10 mm，这与青海省主汛期在6、7、8月份降水集中情况和全年占比一致。从变异系数来看，变异系数呈两峰一谷分布，5候最高(215.9%)，68候次之(200.4%)，最低为32候(40.0%)；其中27候至54候变异系数缓慢波动变化，54候至68候开始变异系数逐渐增大，68候至次年27候转入变异系数减小阶段，说明27候至54候期间候平均降水历年变化不明显，呈常年稳定状态，而54候至68候和68候至次年27候变异系数较大，期间候平均降水变化波动较大。

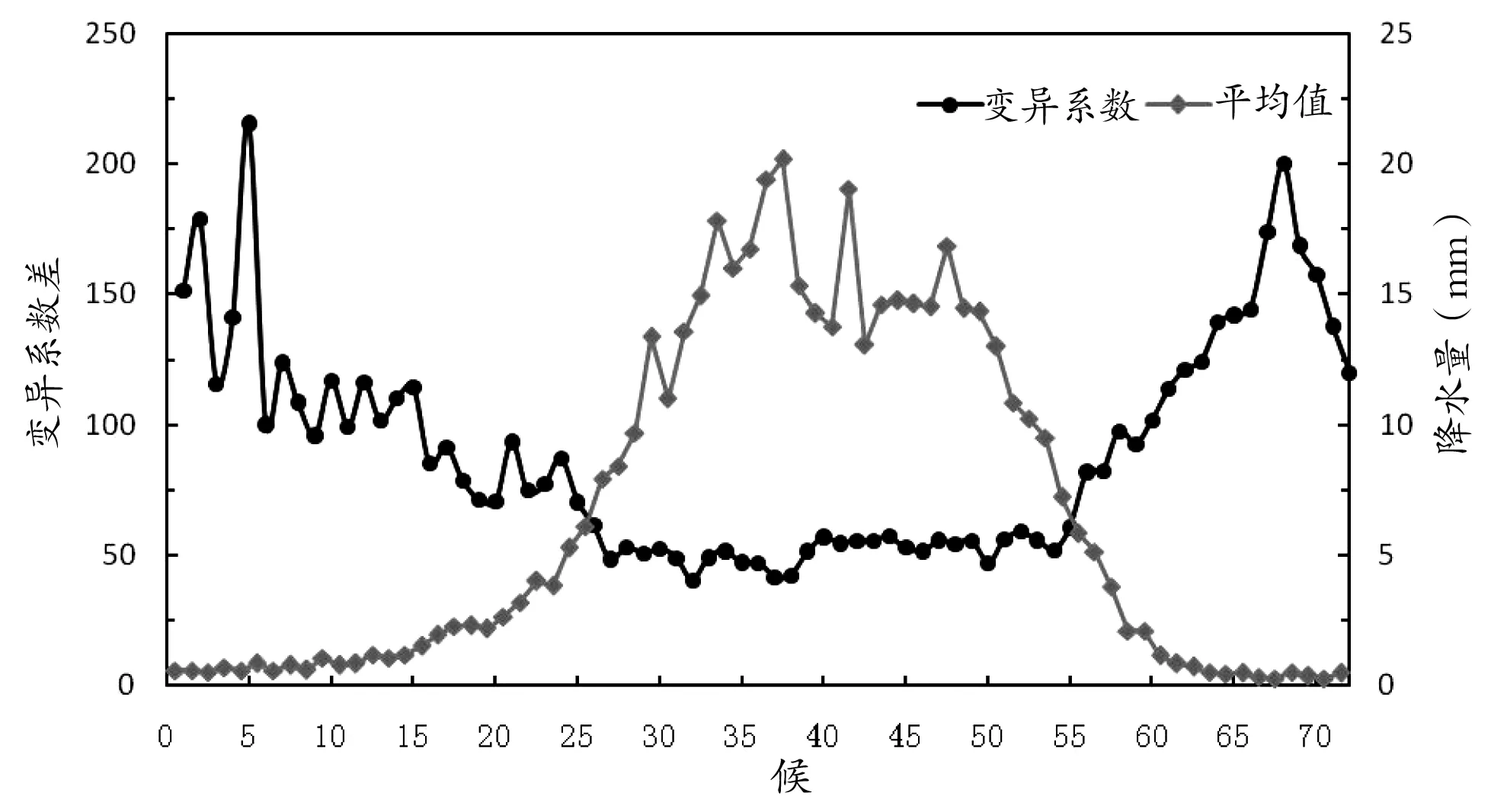
图2 三江源地区候降水量变化及候变异系数

3.2 候平均降水量年际变化

三江源地区1961～2020年候平均降水量总体呈上升趋势(图3和表1)，气候倾向率为0.16 mm/10 a，并通过了0.01显著性检验，多年候平均降水量为6.5 mm，候平均降水量最多是2018年为8.3 mm，1969年最少为5.5 mm。从9年滑动曲线来看，近60年来三江源地区候平均降水量变化大致为3阶段：1961～1988年候平均降水缓慢上升，气候倾向率为0.05 mm/10 a，未通过0.05显著性检验，1989～2002年候平均降水量呈下降趋势，气候倾向率为-0.57 mm/10 a，通过0.05显著性检验；2003年候平均降水量开始转入上升阶段，气候倾向率为0.39 mm/10 a，未通过0.05显著性检验。

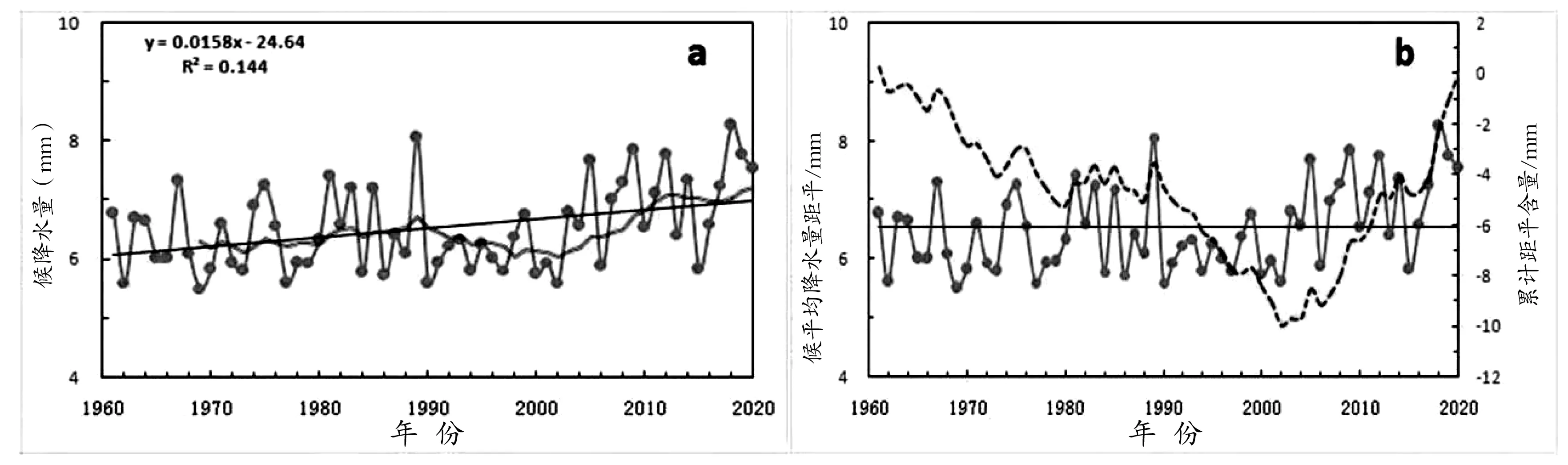
图3 三江源地区候平均降水量年际变化

从累积曲线变化来看，20世纪60年代到21世纪00年代初期，累积距平曲线呈下降趋势，期间候平均降水量比历年候平均降水量偏少的年份有28 a，占比66.7%，比历年候平均降水量偏多的年份有14 a，占比只有33.3%，说明该阶段为降水偏少期，三江源地区气候偏干；21世纪00年代初期以后，累积距平曲线呈上升趋势，期间候平均将水量比历年候平均降水量偏多的年份有15 a，占比83.3%，比历年候平均降水量偏少的年份只有3 a，占比16.7%，表明该期间为降水偏多期，说明进入21世纪初期三江源地区气候由偏干转入偏湿。

6、液压油管疲劳折损。液压油管由于油压变化频繁和油温高，致使管壁张驰频繁，极易出现疲劳折损酿成事故。为有效延长液压油管的使用寿命，最好是用细铁丝烧成弹簧放入油管内作支撑。

表1 三江源地区候平均降水的阶段趋势变化

表2给出了三江源地区候平均降水量的年代际距平变化。可以看出，三江源地区20世纪60年代、70年代和90年代距平均为负，表明候降水量比历史气候值偏少，20世纪80年代、21世纪00年代和10年代距平为正，表明候降水量比历史气候值偏多。

表2 三江源地区候平均降水的年代际距平变化

图4给出了三江源地区各候降水量气候倾向率。三江源地区1961～2020年各候中降水量为正的候数有56候(约占77.8%)，气候倾向率为负的候数有16候(约占22.2%)，说明1961～2020年三江源地区各候降水量总体呈增加趋势。分段来看候降水量气候变化率大致可分为两个阶段：39候至55候气候倾向率波动变化降水有增有减，降水增加的候有7候(约占41.2%)，降水减少的候有10候(约占58.8%)，说明近60年期间候降水量整体持平，无明显增多或减少；56候至次年38候除6个候(约占10.9%)呈减少趋势外，其他49个候(约占89.1%)降水呈现增加趋势，说明该期间1961～2020年候降水量整体增多明显。候降水变化增加最明显的候为33候(1.15mm/10a)，其次是53候(1.00mm/10a)，30候次之(0.96mm/10a)，减少最明显的候是49候(-0.68mm/10a)，其次是42候(-0.66mm/10a)，28候次之(-0.42mm/10a)。

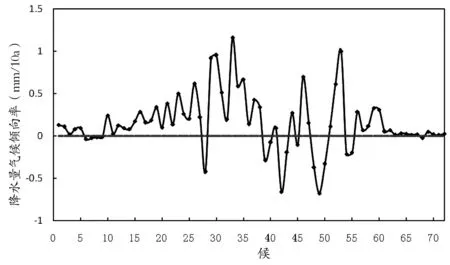
图4 三江源地区降水量候气候倾向率

3.3 气候突变前后差异

青海省平均气温在1997年发生突变[12]，以1997年为界来分析三江源地区降水在气温突变前后的变化关系。从候平均降水量在突变前后差值来看(图5a)，候平均降水量差值为正值的候有51个候，占候总数的70.8%，突变后第30候降水增加最多，增加了4.6 mm，53候次之增加3.7 mm；候平均降水量差值为负值的候有21个候，占候总数的29.2%，突变后降水减少最多的候为42候和50候，分别减少5.2 mm和5.1 mm；总体来说气温突变后候平均降水量增加明显。变异系数在气温突变前后差值来看(图5b)，变异系数差值为正值的候有34个候，占候总数的47.2%；变异系数差值为负值的候有38个候，占候总数的52.8%，总体来说降水候变异系数在气温突变前后无明显变化规律。

从降水量气候倾向率在气温突变前后的变化关系来看(图6)，气温突变前气候倾向率呈增加趋势的候有40候，占总候数的55.6%，呈减少趋势的候有32候，占总候数的44.4%；气温突变后气候倾向率呈增加趋势的候有49候，占总候数的68.1%，呈减少趋势的候有23候，占总候数的31.9%；说明气温突变后，降水量增加趋势的候数明显增多；并且候降水量增加速率明显大于突变前；表明三江源地区候降水量在1997年气温突变后降水增加趋势显著，有利于三江源地区生态的恢复。

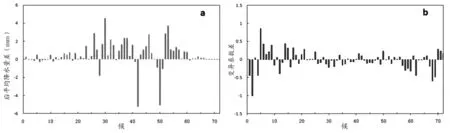
图5 突变前后降水量与变异系数差异

图6 降水量气候倾向率突变前后关系

3.4 雨季开始结束时间确定

以降水相对系数的大小来衡量雨季开始和结束[15]，通过计算各站确定候平均降水相对系数达到1.5，并且连续两候以上，则前面一候确定为雨季开始候，反之为雨季结束候。按此标准求得三江源地区降水起止候与持续候数(表3)。

从整体来看，三江源地区雨季开始候为第30候，雨季结束候为第53候，雨季持续了24个候，充分验证了3.1中降水集中分布在30～53候，可以判识三江源地区自5月31日起全面进入雨季，维持约118 d，于9月25日结束。

从各站来看雨季开始时间在第26～34候之间，最早进入雨季的是果洛久治地区(5月10日)，最晚进入雨季的是可可西里的五道梁与沱沱河(6月20日)；雨季结束时间在第46～57候之间，雨季结束最早的是果洛玛多地区(8月20日)，雨季结束最晚的是果洛久治地区(10月15日)；雨季持续时间最长的是久治，持续32候(约159d)，雨季持续最短的是玛多，持续14候(约67d)。

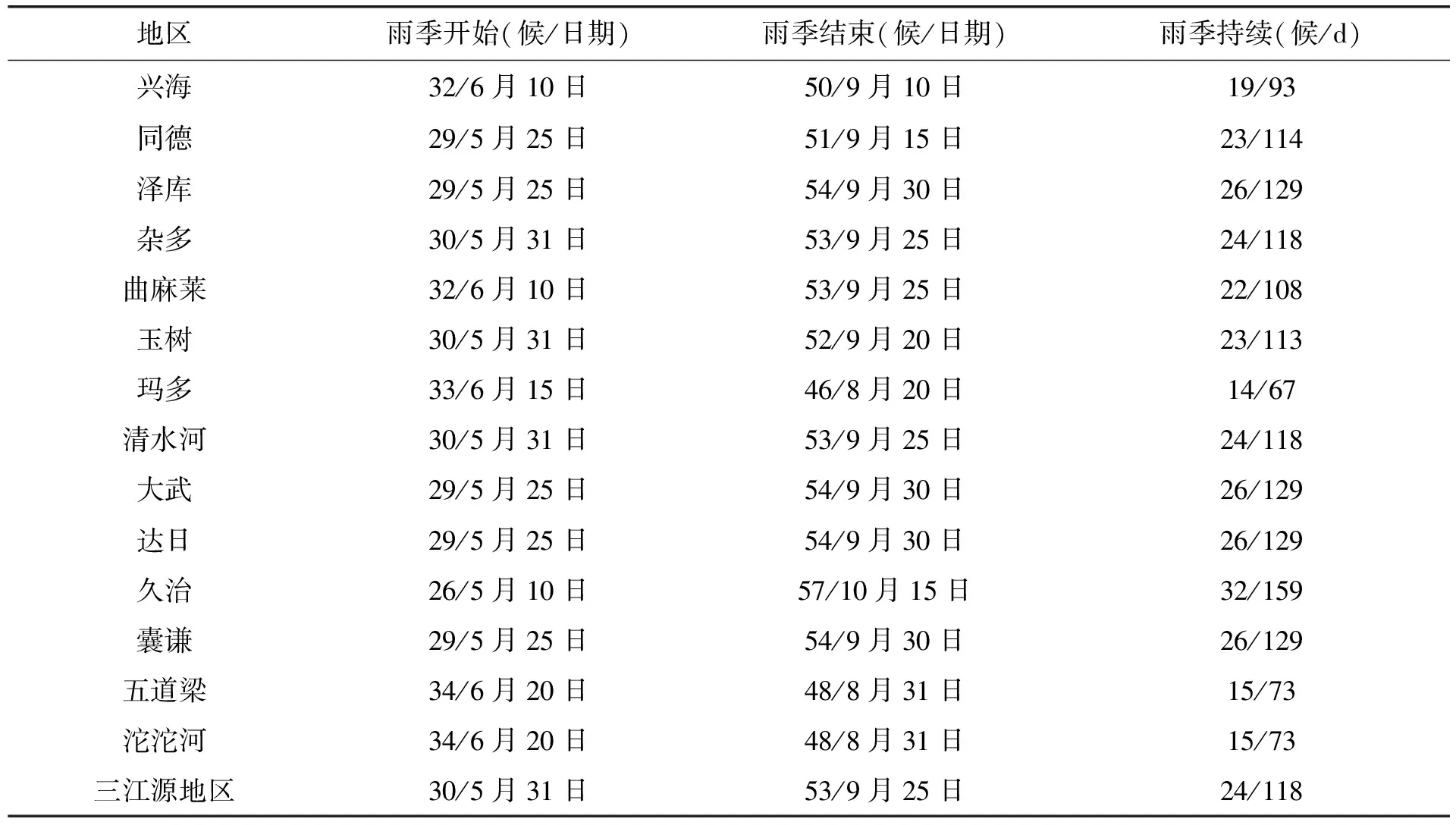
表3 三江源地区降水起止与持续时间统计表

4 结论

利用1961～2020年60 a三江源地区14个气象站点的候降水资料，分析降水量变化特征得到以下结论：

(1)三江源地区候降水量的气候状态呈正态分布，其中降水集中分布在30～53候(持续候数为24候，约占全年33.3%)，各候平均降水量≥10 mm，期间候变异系数缓慢波动变化，说明期间降水常年保持平稳状态，54候至次年29候变异波动先增后减形成双峰状态，期间候降水变化降水变异波动最大的是第5候(215.9%)，68候次之(200.4%)。

(2)三江源地区候降水年际变化呈显著增加趋势，候平均降水量以0.16 mm/10 a的速率增加，各候降水量的气候倾向率为正的候数有56个候(约占77.8%)，增加最明显的候为第33候(1.15mm/10a)。三江源地区20世纪60年代到21世纪00年代初期，为降水偏少期；进入21世纪后，降水明显增多，说明进入21世纪三江源地区气候转湿。

(3)三江源地区候平均降水量在1996年气温突变前后降水变化明显，气温突变后候平均降水量差值为正值的候有51个候，占候总数的70.8%；气温突变后气候倾向率呈增加趋势的候有49候，占总候数的68.1%，并且候降水量增加速率明显大于气温突变前，表明三江源地区候降水量在气温突变后降水增加趋势显著，有利于三江源地区生态的恢复。

(4)三江源地区最早进入雨季的是果洛久治、最晚是五道梁与沱沱河，雨季结束最早的是果洛玛多、结束最晚的是果洛久治；雨季持续时间最长的是久治、最短的是玛多；三江源地区雨季开始候为第30候(5月31日)，雨季结束候为第53候(9月25日)，雨季持续了24个候，持续约118 d。