新媒体支持下的民族地区高中数学微课设计

【摘要】本文以“三角”主题教学为例，论述高中数学微课设计的策略，认为微课设计应遵循紧扣教学目标、紧紧依托学情以及考虑各学校的设施情况三个原则，结合教学实际阐述五个高中数学微课设计具体要求。

【关键词】新媒体 民族地区 高中数学 微课设计

【中图分类号】G63 【文献标识码】A

【文章编号】0450-9889（2022）02-0082-04

随着互联网的高速发展，新媒体呈爆发式增长发展。高中数学微课依托新媒体平台，将视听等多元素结合，把数学知识生动地呈现到学习者的面前。数学微课跨越了时间与空间的限制，逐渐成为高中生新的学习方式。充分利用新媒体平台，依托名优教师的教学资源，建立起符合民族地区学情的数学学习资源库，能为我区高中生提供优质的教学资源。本文以“三角”主题教学为例，阐述高中数学微课的设计方案。

一、微课设计应遵循三个原则

（一）微课设计应紧扣教学目标

在进行微课设计的时候，我们不仅要关注每一课时教学目标的达成，还要关注章节、单元和主题教学目标的相互关系，整体把握，整体设计。三角函数是函数主题下的内容，是学生学习了指数函数、对数函数之后的又一个重要的函数。《三角函数》一章的课程目标是通过实例，学习三角函数及其性质，体会三角函数在解决具有周期变化规律问题中的作用;而《解三角形》一章是在学习了《三角函数》相关知识的基础上，通过任意三角形边角关系的研究，发现并掌握三角形中边与角的数量关系，并在生产生活中能够运用所学知识解决测量和几何计算有关的实际问题。

在制订微课教学目标过程中，教师还可以借助布鲁姆教学目标制订教学计划。布鲁姆教学目标分析指出认知领域的教育目标从低到高可以分为六个层次：识记、理解、应用、分析、综合、评价。

表1 布鲁姆教育目标分类表

[知识维度 认知过程维度 识记 理解 应用 分析 综合 评价 事实性知识 概念性知识 程序性知识 反省认知知识 ]

（二）微课设计应紧紧依托学情

不同班级、不同学校的学生的数学基础、学习习惯、运算能力和思维水平等存在差异。在学习高中数学“三角”这一板块内容之前，学生已经学习了集合、函数、圆的方程等知识，具备进一步学习三角函数的基础。但是，不同层次的学生之间仍存在着较大的差距，尤其表现在对三角知识的探究、联想以及迁移上。生源基础薄弱的学校，应注重基础知识、课本核心概念的微课设计，根据实际情况还需要加上必要的典型例题和对应的巩固练习。生源基础较好的学校可以把易错点、难点的数学知识归纳总结成微专题，进而将其录制成微课供学生学习，还可在微课的最后设计附上思维拓展的变式试题和答案，供学有余力的学生课后自主学习。但是不论设计什么类型的微课，最终目的都是达成课程标准提出的提升学生数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等数学学科核心素养。

（三）微课设计应考虑各学校的设施情况

学校的信息技术软件和硬件不同，微课设计的方案也不同。信息技术硬件软件设施较落后的学校，可以将制作完成的微课拷贝到教室电脑或者教师办公室的电脑，供学生学习。而信息技术硬件软件设施较好的学校，则可以通过班级希沃电脑、平板电脑、班级微信公众号、视频号、哔哩哔哩网站、班级QQ群、广播电视点播系统等发布微课，供学生在不同的时间和空间学习。

二、例析高中数学微课设计

下面，笔者以南宁市第三中学高中部五象校区为例，阐述高中数学微课设计策略。南宁市第三中学高中部五象校区生源较好，绝大多数学生有比较好的学习基础和学习习惯。对数学学科而言，学生掌握的数学基础知识、拥有的数学基本技能、领悟的基本数学思想、积累的数学基本活动经验都是比较丰富的，但是他们在发现和提出数学问题、分析数学问题、解决数学问题等方面略有不足，对一些核心概念、重要的公式定理的推导，在课堂学习中不能快速地接受并理解。从学生完成配套练习《新课程测评》、活页习题和周测试题的反馈来看，有些题型他们屡屡犯错，教师可以将这些问题归纳总结，形成微课供学生学习。

南宁市第三中学高中部五象校区拥有较好的信息技术硬件和软件，每位教师都配置性能较好的电脑，每个班级都配备希沃电脑，学校网络全覆盖。良好的技术支持为本校区开展微课设计提供了强大的保障。教师可以将制作好的微课拷贝到班级希沃电脑，发布到班级QQ群、班级微信公众号、视频号、哔哩哔哩网站和广播电视点播系统等平台，供学生在不同的时间和空间任意学习。

根据本校区学情，教师在制作数学微课时，应符合以下几个要求。

（一）核心數学概念和重要的公式定理应重点录制

数学概念是数量关系和空间形式本质特征的反映形式，是数学基础知识的重要组成部分。数学概念的内涵和外延组成了数学概念的本质。在进行数学核心概念的微课设计时，教师应该创设情境，精心设计数学活动，让学生经历发现、分析、提炼、升华等过程，加深对核心数学概念的理解。

在《三角函数》一章中，核心的概念和公式定理有任意角的三角函数、三角函数线、同角三角函数的关系、三角函数的诱导公式、正弦函数和余弦函数的图象与性质、正切函数的图象与性质、函数y=Asin（ωx+φ）的图象与性质、三角函数模型的简单应用，等等。教师需要针对这些核心的数学概念和重要的公式定理，精心设计微课。

在学习核心概念正弦定理的过程中，用多种方法探究证明正弦定理是学生学习的难点，针对此难点，笔者制作了微课进行突破。

设计探究一

在[]ABC中，角A，B，C所对的边长分别为a，b，c.若[]ABC是直角三角形，不妨取C=90°，则sinA=[ac]，sinB=[bc]，从而[asinA]=[bsinB]=c，又因为C=90°，所以sinC=1，所以[asinA]=[bsinB]=[csinC].若[]ABC是等边三角形，因为A=B=C，a=b=c，上述优美的关系式无疑也是成立的.对于一般的三角形，上述优美的关系式还成立吗？易得在[]ABC中，角A，B，C所对的边长分别为a，b，c，则各边和它所对角的正弦的比相等，即：[asinA]=[bsinB]=[csinC].

设计探究二

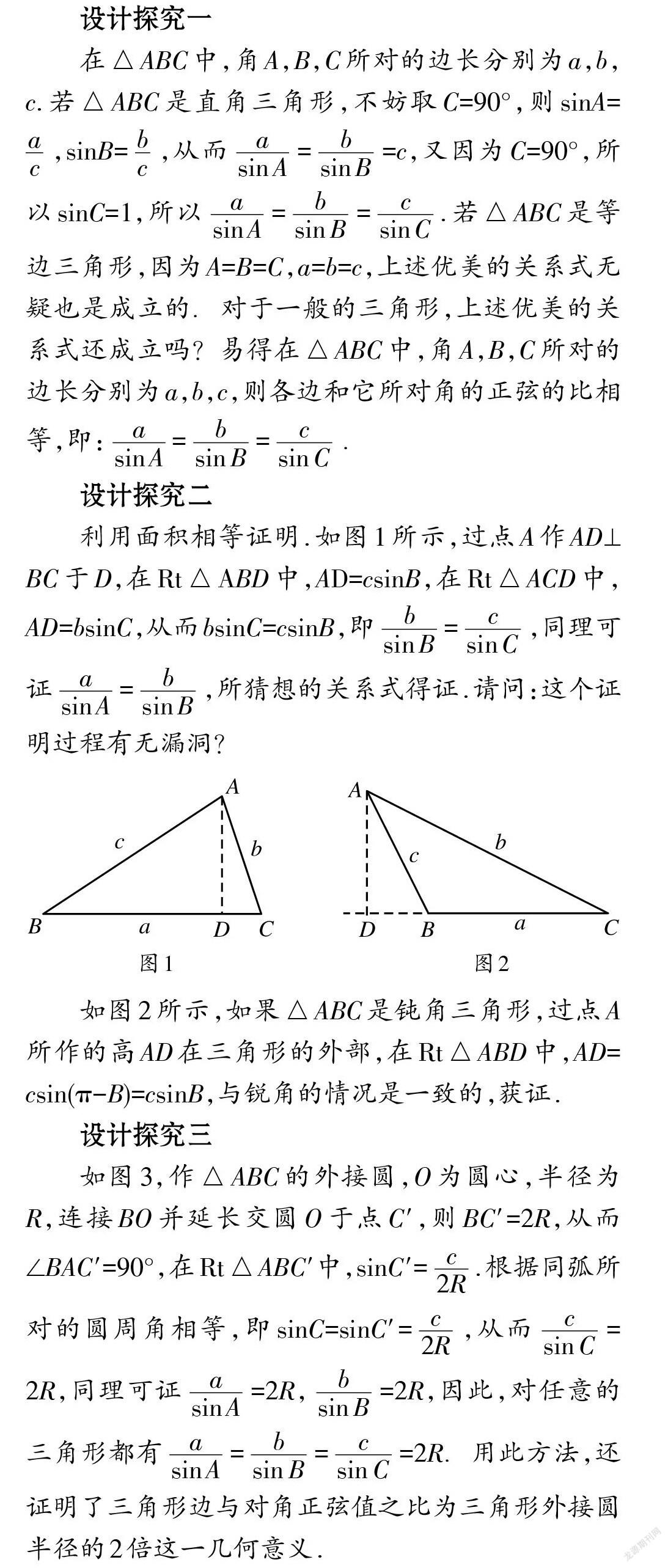
利用面积相等证明.如图1所示，过点A作AD⊥BC于D，在Rt[]ABD中，AD=csinB，在Rt[]ACD中，AD=bsinC，从而bsinC=csinB，即[bsinB]=[csinC]，同理可证[asinA]=[bsinB]，所猜想的关系式得证.请问：这个证明过程有无漏洞？

如图2所示，如果[]ABC是钝角三角形，过点A所作的高AD在三角形的外部，在Rt[]ABD中，AD=csin（π-B）=csinB，与锐角的情况是一致的，获证.

设计探究三

如图3，作[]ABC的外接圆，O为圆心，半径为R，连接BO并延长交圆O于点C′，则BC′=2R，从而∠BAC′=90°，在Rt[]ABC′中，sinC′=[c2R].根据同弧所对的圆周角相等，即sinC=sinC′=[c2R]，从而[csinC]=2R，同理可證[asinA]=2R，[bsinB]=2R，因此，对任意的三角形都有[asinA]=[bsinB]=[csinC]=2R.用此方法，还证明了三角形边与对角正弦值之比为三角形外接圆半径的2倍这一几何意义.

设计探究四

如图4，在[]ABC中建立平面直角坐标系xOy，点C在y轴上的射影为C′，则[AC]与[BC]在y轴正方向上的射影相同，分别为：[AC]cos（A-90°）=bsinA，[BC]cos（90°-B）=asinB，所以bsinA=asinB，即[asinA]=[bsinB]，同理可证A为锐角或者直角时关系式成立.

（二）抓住教学的重点和难点，有效突破

数学教学的重点和难点往往是学生掌握不到位的知识点，也是学生学习数学过程中的认知障碍，导致数学思维堵塞的源头。这些数学重点和难点如果不能有效突破，会成为学生进一步学习的绊脚石。如何帮助学生有效突破学习中的重点和难点，应该是微课设计需要重点考虑的问题。

在微课设计中借助数学实验和几何画板等工具进行验证是有效突破数学教学中的重点和难点的有效途径。比如教学人教A版必修5第一章《解三角形》余弦定理的推导，教师设置问题：在任意[]ABC中，它的三角A，B，C与对应的三边a，b，c存在怎样的关系？并利用几何画板，任意改变三边和三角的值，让学生观察边和角的变化关系，引导学生大胆提出猜想。在大边对大角的前提下，是否还有其他体现数学对称性和几何美的性质？学生提出几组大胆的猜想，教师通过操作几何画板一一验证猜想，发现不论角和边如何改变，a2=b2+c2-2bccosA这个猜想是恒成立的，接下来便是严格的数学证明。突破证明余弦定理这一难点的微课设计如下。

探究活动一

当A是锐角时，过点C作CD⊥AB，交AB于点D，则在Rt△ACD中，AD=bcosA，CD=bsinA.

从而，BD=AB-AD=c-bcosA.在Rt△BCD中，由勾股定理可得BC2=BD2+CD2=c2-2cbcosA+b2=c2-2cbcosA+b2.

即a2=b2+c2-2bccosA.

同理可证A是直角或者钝角的情况.

探究活动二

用平面向量法证明.

在△ABC中，由[BC]=[AC]-[AB]可得：[BC]=[AC-AB].

∴[BC2]=（[AC-AB]）2=[AC2]+[AB2]-2[AC]·[AB]=[AC2]+[AB2]-2[AC]·[AB]cosA=b2+c2-2bccosA.即a2=b2+c2-2bccosA.

探究活动三

利用坐标系法证明.如图5.

以A为原点，边AB所在直线为x轴，建立平面直角坐标系，证法如下：点C的坐标为（bcosA，bsinA），根据两点间的距离公式得[BC]=[（bcosA-c）2+（bsinA-0）2].整理化简得a2=b2cos2A-2bccosA+c2+b2sin2A.即a2=b2+c2-2bccosA.证明完毕.

（三）组合典型例题和习题，形成微专题

理论与实践相结合是学习的有效途径。在学习核心概念以后，借助典型例题的讲解可以帮助学生快速掌握所学知识。课本中的例题、习题都是编者精心设计的，有效利用它们可以起到举一反三的效果。结合课本“探索与发现”栏目可以拓展学生学科阅读能力，课外探索数学的能力。

以必修5中的例题为例：在[]ABC中，已知a=20cm，b=28cm，A=40°，解三角形（角度精确到1°，边长精确到1cm）。这是经典的三角形解的个数问题，并且题目特意给的是非特殊角，课堂教学必须使用计算机辅助教学才能完成。在完成此例题后，教师引导学生阅读“探究与发现”栏目“解三角形的进一步讨论”，通过几何画板设计已知角A是锐角，且a<b时分三种情况动态展示a<bsinA，a=bsinA，a>bsinA。这样一来，教师巧妙利用课本的例题、习题和“探索与发现”等材料制作微课专题，有效突破难点。

（四）典型错题应呈螺旋式上升分层设计

美国教育学家布鲁纳提出“螺旋式上升”的教育理念，其目的在于培养儿童出色的智力，即在不同时间学段出现类似的学科教学内容，利用儿童缓慢上升发展的智力水平，不断加深和拓展学科内容。瑞士教育学家皮亚杰把儿童认知发展划分为四个阶段，即感知运算阶段（0—2岁）、前运算阶段（2—7岁）、具体运算阶段（7—11岁）、形式运算阶段（11岁后一直发展）。当儿童的低层次的智力水平的平衡被冲击后，平衡能在更高一级的水平得以恢复。我们新课程数学课本内容是按照这些儿童认知规律编排的，教师在进行微课设计时，应遵循螺旋式上升分层设计原则。

比如关于三角函数ω问题是典型的错题，如何针对这些错题设计微课教学？教师可以先设计一个条件的ω情况，比如题目：已知函数f（x）=sin[ωx-π4]（ω>0）在（0，2π）上有且仅有两个零点，则ω的取值范围是？再比如题目：已知函数f（x）=sinωx+cosωx（ω>0），若f（x）在[0，2π]恰有3个最值点，则ω的取值范围是？在学生能够正确解答这些一个条件的ω情况题目之后，教师再设计两个条件的ω情况，比如题目：已知函数f（x）=sin（ωx+φ），其中ω>0，[φ]≤[π2]，[-π4]为f（x）的零点，且[f（x）≤][f（π4）]恒成立，f（x）在[-π12，π24]区间上有最小值无最大值，则ω的最大值是？通过这样分层练习，学生的学习能力能够得到螺旋式提升。

（五）应具备复习、测验和评价功能

复习是高中数学教学过程中一个非常重要的环节，它可以整合旧知形成知识结构。利用思维导图整理数学知识树是一个有效的复习方法。

测试和评价常见的形式为课堂提问、课堂观察、作业批改、书面测试、错题整理和错题重做等。书面测试可分为微测试和周测等，微测试共六题，其中选择题四题、填空题两题;周测共十二题，其中选择题六题、填空题四题、大题两题。选择题改卷均通过“门口易测网”App实现，学生考试结束后可以立即通过该App查看得分情况，也可以查看详细的解答过程;教师通过该App可以查看“班级报告”“试题报告”“试题分析报告”“知识点报告”和“比较报告”等，详细了解学生的评价情况。比如我们在一次微测试中设计了六道题，题目知识点囊括了已知两角及一边解三角形、已知两边及一边的对角解三角形、三角形解的个数、三角形面积公式、简单恒等变形、边角互化、辅助角公式等，测试的评价反馈为我们下一步的教学准备提供了数据支持。

充分应用新媒体辅助高中数学教师课堂教学和学生数学学习是一条行之有效的途径。但是，收集、筛选、整理优质数学资源，根据学情进行微课的录制，会耗费教师大量的时间和精力。本文在理论的基础上，结合实践阐述如何有的放矢设计微课。我们在实践的过程中有可能会出现很多问题，但是我们一边实践一边改进，在实践与改进中完善设计，定能探索出一条符合学情特点的、能够有效提升高中数学教学效果的可行之路。

参考文献

[1]李耀光，何小亚.新课程数学概念“螺旋式”上升编排的认知审视[J].数学教育学报，2010（4）.

[2]史宁中，林玉慈，陶剑，等.关于高中数学教育中的数学核心素养：史宁中教授访谈之七[J].课程·教材·教法，2017（4）.

注：本文系广西教育科学规划2021年度A类课题“新媒体支持下优化民族地区高中数学教学的实践探究”（编号：2021A047）的研究成果。

作者简介：陈烈（1979— ），广西北流人，高级教师，教育学硕士，研究方向为基础教育。

（责编 刘小瑗）