博弈论思想下的主播激励策略数学模型研究

张佳欣，陆媛媛

数学的价值在于应用，运用数学模型分析经济现象和经济问题已经成为世界各国应用数学研究的主流和趋势.当前，随着互联网的普及，网络直播已经成为我国一个具有巨大经济规模的新兴行业，运用博弈论思想，建立数学模型，构建函数，进行行业数据分析，可以实现最优化监管、最有效激励、最大化利润.

网络直播的运行模式是以平台主播为核心，主播与观众通过直播间实时进行网上交流互动[1］.观众根据对主播的满意度随机赠送网络礼品，从而让主播和直播平台实现收益.网络观众对主播的打赏行为在一定程度上反映了观众对主播的认可度，也使观众产生更大的参与感和体验感，从而获得心理上的满足.

目前，网络直播在诸多方面直接或间接地影响着人们的生活，越来越多的人喜欢观看直播，而且直播观众具有一定的跟随性，在某种程度上，受网络外部性的影响越来越明显.也就是说，消费者效应受到观看直播的用户规模的影响越来越大[2］.与此同时，为了保证直播行业的健康稳定发展，直播平台的监管非常重要.要规范行业标准，实行以法律标准为底线的最优监管制度[3］.针对上述情况，可以运用博弈论思想，对网络直播相关问题建立数学模型加以研究，从而精确分析网络外部性因素、主播个人努力程度、平台监管力度、平台激励策略等对网络直播收益的影响，精准把握网络直播平台的发展现状，从而进行科学、合理、有效地决策.

1 问题描述

通过分析网络外部性因素影响下、处于直播平台监管下的网络主播和直播平台的期望利润，研究主播的最优努力水平和直播平台的最优监管力度，分析网络外部性因素对平台和主播的影响，分析直播平台对主播实行激励的最优决策，进一步探索直播行业获取更大利润和良好发展的最佳策略.

2 符号说明与假设

假设网络主播的努力水平集合为A，e∈A表示网络主播特定的努力水平，设定e是一维的连续变量，e越高，表示主播越努力；直播平台的监管水平集合为B，g∈B表示直播平台特定的监管水平，设定g是一维的连续变量，g越高，表示直播平台的监管力度越强；假设平台监管对主播的表现有正向激励作用，平台的监管程度越强，主播越努力对直播进行改进和提高，从而主播表现越优秀，则主播在平台监管下的表现函数为ae+bg+ε，a∈( 0,1 )表示主播努力水平的弹性因子，b∈( 0,1)表示直播平台监管水平的弹性因子，ε∈N（0，σ2）表示与主播个人努力水平和直播平台监管水平无关、影响主播表现效果的其他因素（Eε= 0），如主播的知名度、直播环境、主播外形魅力和性格特点等[4-5］.

假设观众浏览直播并对主播进行网络礼品打赏后获得的效应函数为u=η-p+β(ae+bg+ε)+αQ，其中η∈( 0,1 )表示观众浏览直播并对主播进行网络礼品打赏所获得的满足感的货币化，p表示观众对主播打赏的网络礼品的价格（假设观众打赏的网络礼品是唯一的且价格不变），β∈( 0,1 )表示观众在浏览直播的过程中所获得的满足感的货币化，体现了观众对主播的认同与喜爱水平，α∈( 0,1 )表示网络外部性系数，Q表示给主播打赏的观众数量.

假设直播平台通过底薪和激励两部分支付给主播工资，即主播工资表达式为S(Q)=f+λQ，其中f表示直播平台给主播支付的基础工资，λ∈( 0,1 )表示直播平台按照给主播打赏的人数实行激励的数量激励系数[6］.

Hotelling 模型把观众视为在一个单位距离内的均匀分布，假设观众通过观看直播获得的满意程度的货币化η均匀分布在[ 0,1 ]区间，观众给主播打赏、不打赏的行为位于这个区间的两个边界点，令u= 0，可计算出观众观看直播时打赏与不打赏的效用无差异点η*=p-β(ae+bg+ε)-αQ，因此可得到打赏的市场需求，即给主播打赏的观众数量表达可见，打赏的数量与打赏礼物的价格、主播的个人努力水平、直播平台的监管水平、观众对主播的满意度和网络外部性因素有关[4］.各参数符号表示含义如表1 所示.

表1 符号说明

3 模型建立与求解

根据逆向求解的步骤，首先分析网络主播期望收益模型.

定理1 当直播平台给出最优数量激励系数和最优监管水平决策时，主播根据直播平

性质1 主播为直播所付出的努力程度与直播平台根据给主播实行打赏的观众人数所实行激励的数量激励系数表现为正相关.

收益函数中，并将EY分别对λ和g求偏导有

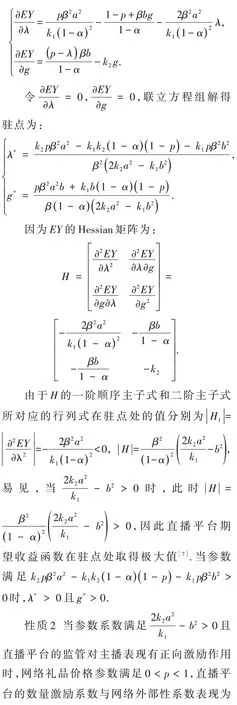
此直播平台的监管水平与网络外部性系数表现为正相关，即网络外部性系数越大，直播平台的监管力度越大.这表明，观看直播的观众越多，可能会产生的问题越多，因此，应该加强监管，监管力度越大，主播的表现越好，进而确保一个更加安全稳定的直播环境[9］.

4 系统最优决策

将λ*代入定理1 主播的最优决策e*中，得

进而将最优决策值代入期望利润函数中，可以获得在网络外部性下处于直播平台监管的直播平台和签约主播的最优期望利润.

5 算例分析

目前，我国有许多受到大众广泛关注的直播平台，如：抖音、快手平台等.假设有某一直播平台，某一主播在该平台进行直播，假设系统参数满足p= 0.9（千元），k1= 0.1，k2=0.9，a= 0.5，b= 0.8，β= 0.5，α= 0.7，f= 1（千元），分析直播平台和主播的最优决策和最优利润，计算结果如表2 所示.

表2 最优算例结果

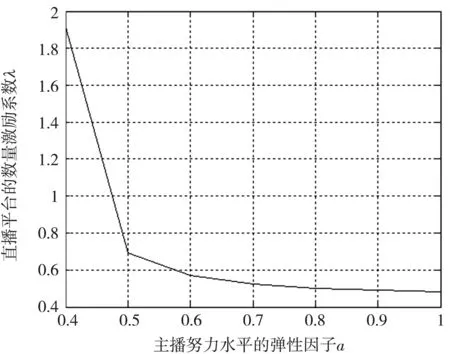
图2 直播平台数量激励系数变化

由图1~图3 可以看出，随着主播努力的弹性因子的增加，主播的努力水平呈现递增趋势；直播平台数量激励系数呈现递减趋势；直播平台的监管水平呈现递减趋势.

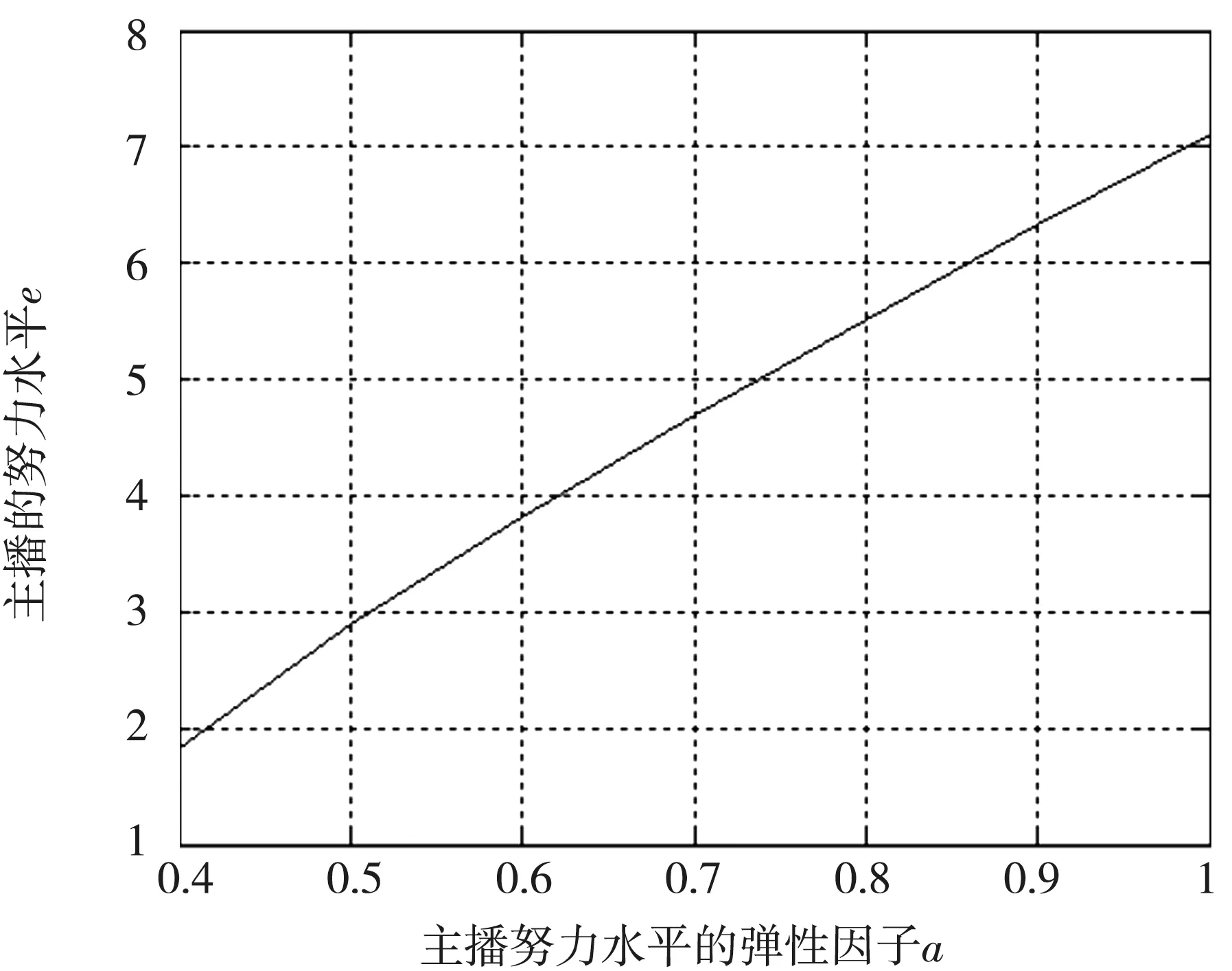
图1 主播努力水平变化

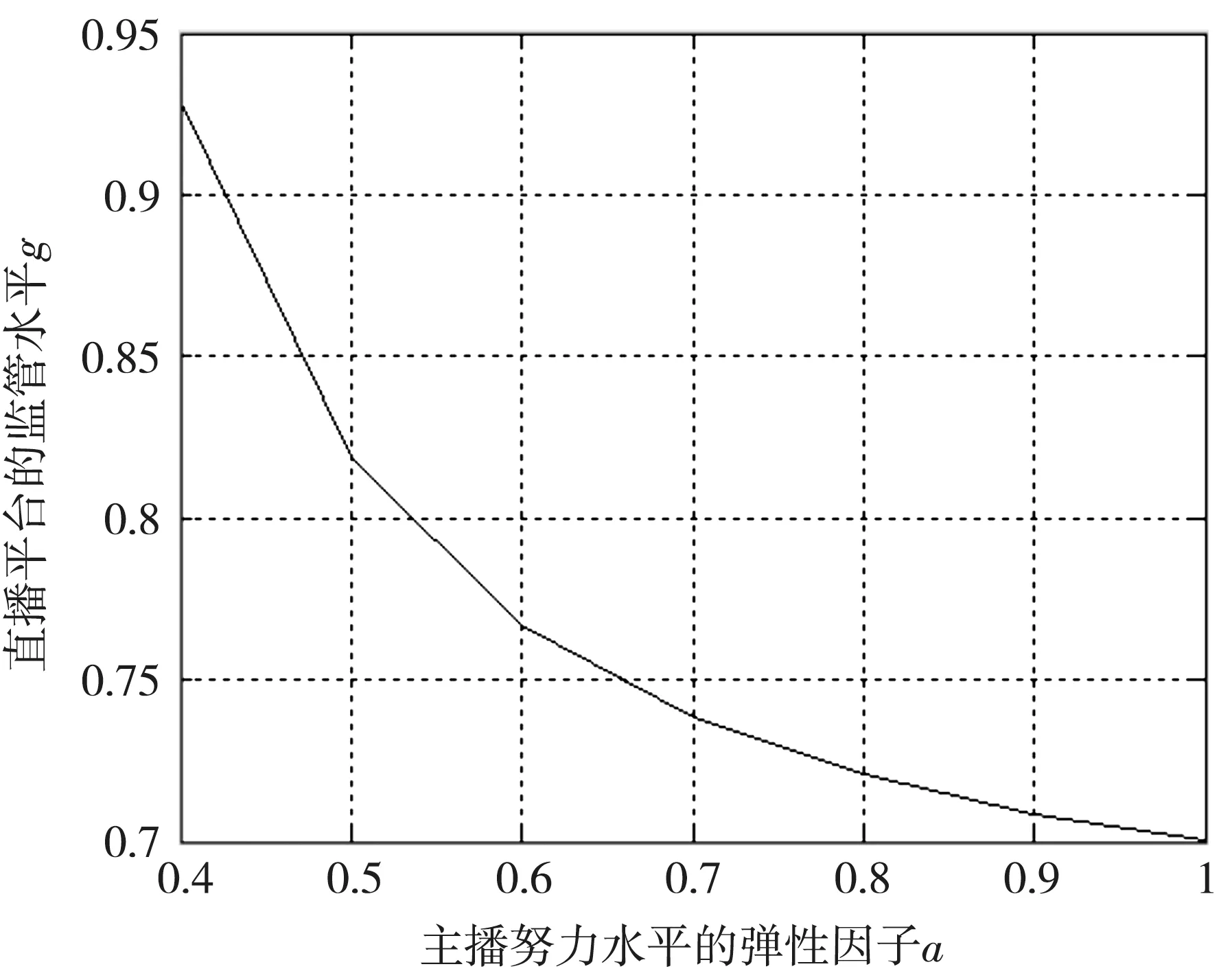
图3 直播平台监管水平变化

6 结语

由以上数学模型可以看出，当直播平台的监管对主播表现起正向激励作用时，若网络礼品价格较低，那么网络外部性影响就越强，相应地，直播平台给予主播的数量激励系数就越高，从而主播付出的个人努力也越大.同时，网络外部性加强，直播平台实施监管的强度也随之增加.具体来讲，由于网络直播受网络外部性因素影响，观看直播的用户数量越大，直播对观众的吸引力越增加；若平台给网络礼品的定价较低，则对主播的激励程度越大，会使主播更致力于直播的精进与改善，把直播做得更好，从而使网络观众给主播进行更多的礼品打赏，主播和平台获得的利润更高.与此同时，在观看直播的用户人数增多的情况下，直播平台需要加强对主播的直播内容等方面的监管，使直播的表现更加优秀，从而在创造利益最大化的同时，营造更加文明、健康、稳定的网络直播环境[10］.