IRS辅助的多天线系统下行链路低复杂度信道估计*
李素月,郝红婷,王安红
(太原科技大学 电子信息工程学院,太原 030024)
0 引 言
智能反射面(Intelligent Reflective Surface,IRS)技术的提出,很好地适应了未来蜂窝网络的需求。一般来说,IRS是一个由大量无源反射单元组成的平面,每个单元都能够独立地对入射信号进行诱导,从而可以控制振幅或相位的变化,使发射机和接收机之间的信道可以实现灵活的配置。IRS为无线通信系统提供了一种新的手段,从根本上解决了无线信道衰落损害和干扰问题,并有望实现无线通信容量和可靠性的大幅度提升[1]。
然而,IRS的引入带来了新的挑战,其中获取信道状态信息(Channel State Information,CSI)是比较困难的工作,这是由于为了实现低成本和低功耗,IRS采用无源设计,不配备射频链,因而导致它没有能力完成信道估计。尤其是除了估计基站(Base Station,BS)和用户设备(User Equipment,UE)之间的直接信道之外,还需要估计两个IRS辅助信道,即BS到IRS的信道和IRS到用户的信道。
信道估计一直是无线通信系统中重要的研究课题之一,不同的系统和信道建模对信道估计带来不同的挑战。学者们在关于IRS的一些研究工作中提出了各自有效的信道估计方法[2-4]。对于单天线下行链路系统,文献[2]研究了IRS辅助的环境反向散射系统的信道估计,通过初始估计和迭代估计获得信道参数,并进一步推导了信道的克拉美罗界(Cramer-Rao Lower Bound,CRLB)[3]。另一方面,对于多天线上行链路系统,文献[4]利用压缩感知技术将级联信道构造成块稀疏信道矩阵恢复问题,不考虑用户和BS之间的直接链路。此外,文献[5-6]提出了一种基于最小二乘(Least Squares,LS)估计准则的IRS辅助单用户上行链路系统信道估计协议。文献[6]假设在一段相干时间内信道保持恒定不变且保证IRS在整个信道估计阶段处于工作状态下,分别估计了直接链路和级联信道,最后使用IRS相移矩阵和最小方差无偏估计的结果进行优化设计。针对IRS上行多用户通信,文献[7]提出了一种基于导频的三阶段的信道估计框架:在第一阶段和第二阶段分别估计基站与用户的直接信道和一个典型用户的反射信道;在第三阶段,利用其他用户与典型用户的强相关性,以较低的导频开销估计其他用户的反射信道,其中在信道估计阶段,IRS相移矩阵基于离散傅里叶变换(Discrete Fourier Transform,DFT)矩阵获得;最后总结出信道估计所需的最小导频长度为2K+N-1(K为用户数,N为IRS反射单元数)。
然而IRS信道估计的多数文献是关于上行链路的,据调研,目前几乎没有针对IRS辅助多天线系统的下行链路低复杂度信道估计的研究。为此,本文以文献[2]为研究基础,将其IRS单天线系统模型扩展到多天线。利用反向散射信号控制IRS的各个反射面,分两个阶段进行直接链路和级联反射链路的信道估计。在传统LS算法推导的基础上,研究Gauss-Seidel(GS)迭代算法,避免矩阵求逆,降低了计算复杂度,仅需较少迭代次数。为了进一步评估系统性能,进行了CRLB的推导。在仿真实验环节首先仿真了下行链路导频生成方式和导频长度对估计算法的影响,然后通过对比LS算法和GS迭代算法的均方误差(Mean Square Error,MSE)性能,验证了所提出算法的有效性。
1 系统模型
考虑一个如图1所示的IRS辅助的下行链路通信系统模型,BS通过下行链路与一个单天线用户通信,其中BS配有M根天线,IRS包含N个反射元素。h∈M×1表示BS到用户的直接链路信道增益,pn∈M×1表示BS和IRS的第n(1≤n≤N)个反射元素的信道增益,qn∈为IRS的第n个反射元素和用户之间的信道增益。

图1 下行IRS辅助系统
根据系统模型,在时刻i,用户接收到的信号可表示为
(1)
式中:x(i)∈1×M为BS发射的导频信号;φn,i表示IRS的相位和衰落的影响;w(i)表示均值为零且方差为σ2的独立同分布的加性高斯白噪声;c(n)表示向用户传递二进制信息位的反向散射信号,取值为0或1,也可用来控制IRS的工作状态。
把式(1)中的第二项表示为级联反射信道,即
(2)
需要指出的是,IRS的反射元素的个数及相移设计,与级联信道g的估计精度无关。
由于用户端的功率和处理能力受限,需要采用低复杂度的信号处理技术。接下来从基础的LS算法出发,探索低复杂度的信道向量h和g的估计方法。
2 算法推导
2.1 LS估计算法
假设信道在一段相干时间内保持恒定不变,考虑的信道估计分两个阶段完成。在第一阶段,先估计直接链路信道h,假设第一阶段的导频长度为K0。此时令IRS保持关闭状态,即c(n)=0。基于式(1),用户接收到的信号表示为
u0=X0h+w0。
(3)
式中:u0=[u(1),u(2),…,u(K0)]T是K0×1维的接收向量,X0=[x(1);x(2);…;x(K0)]是K0×M维的发射导频矩阵,w0=[w(1),w(2),…,w(K0)]T表示服从零均值且方差为σ2的独立同分布的加性高斯白噪声向量。在此统一说明:公式中上标T和H分别表示向量或矩阵的转置及共轭转置运算。
在第二阶段,主要任务是估计级联信道g。假设采用K1个导频符号,此时令IRS处于工作状态,即c(n)=1。基于式(1),用户接收到的导频信号向量为
u1=X1h+X1g+w1。
(4)
式中:u1=[u(1),u(2),…,u(K1)]T是K1×1维的接收向量,X1=[x(1);x(2);…;x(K1)]T是K1×M维的发射导频矩阵,w1=[w(1);w(2);…;w(K1)]T表示加性高斯白噪声向量。这里,两阶段采用的总导频长度记为Kp=K0+K1。
将式(3)和式(4)合并起来,可得
(5)
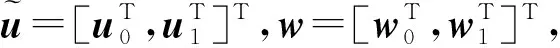
(6)
因此,可以得到
(7)
式中:t=[h,g]T为要估计的信道向量。
由式(7),利用LS算法,信道向量的估计结果为
(8)
式中:
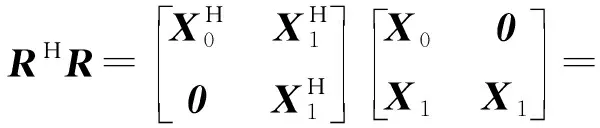

(9)
将式(9)代入式(8),可得

(10)
通过式(10)得出直接链路和反射链路的LS信道估计结果分别表示为
(11)
(12)
需要说明的是,式(8)中求逆矩阵F的维数是2M×2M,式(11)和式(12)中求逆矩阵的维数均为M×M。可见式(11)和式(12)相对于式(8)维数减少一倍,大大降低了矩阵求逆的计算复杂度。
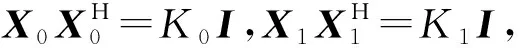
(13)
(14)
2.2 GS估计算法
已知对于下行大规模MIMO系统,信道矩阵R的列是渐近正交的[8]。因此通过将任意2M×1的非零向量表示为e,可以得到eHFe=(Re)HRe>0,这说明矩阵F是正定的。此外,通过FH=(RHR)H=F,可以进一步得出矩阵F是厄米特(Hermitian)正定的。

(15)
式中:上标i∈表示迭代次数。
正如前面所提到F是厄米特正定的,因此也可以将F分解为
F=D+L+LH。
(16)
式中:D=diag(diag(F))为对角矩阵,而且L和LH是F的对角线以外的上三角和下三角矩阵。式(8)的形式等价为Ft=z,用GS迭代算法来表示如下:
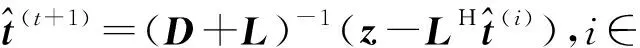
(17)

需要注意的是,由于矩阵F是厄米特正定的,因此所采用的GS迭代算法对于任何初始解都是收敛的(收敛条件:迭代矩阵((D+L)-1LH)的谱半径小于1,其中谱半径指的是其矩阵特征值的绝对值的最大值[10])。接下来将通过对比计算复杂度,说明GS迭代算法相比LS算法的优越性。
2.3 复杂度分析
由于复杂度主要由复数乘法的次数决定,考虑用复乘数对计算复杂度进行分析。基于式(16)中D和L的定义,式(17)的解可按元素表示为
(18)
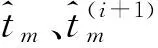
表1通过公式比较了LS算法和GS迭代算法的复杂度,可以看出,对于公式(8),LS算法的复杂度为O(8M3),而GS迭代算法的复杂度为O(4M2),低了一倍。而为了保证近似性能,通常需要更多的乘法计算。相比较而言,GS迭代算法所需的乘法计算次数更少,能够进一步降低整体方案的复杂度。
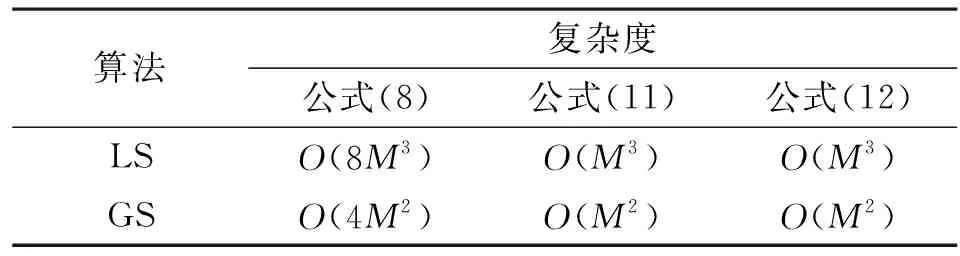
表1 复杂度对比
3 CRLB推导
CRLB经常被用来计算理论达到的最佳估计精度以评估参数的性能。接下来用CRLB推导算法的理论性能。
基于式(7)可知,向量是要被估计的参数,其中t[1∶M]=h,t[M+1∶2M]=g。
已知对于每个参数t「i⎤,i=1,…,M,…,2M,它的CRLB可以作为Fisher信息逆矩阵的第「i,i⎤个元素,由此可得出
var(t[i])≥CRLB(t[i])=[I-1(t)]ii。
(19)
式中:var(t[i])表示t[i]的方差;I(t)是维数为2M×2M的Fisher信息矩阵,其中I(t)的第[i,j]项可定义为
(20)
式中:i,j=1,…,M,…,2M。
根据式(7)和式(20),以天线数M=2为例,可得维数为4×4的Fisher信息矩阵I(t)为
(21)
式中:ln表示对数运算,p(u;t)表示随机向量u对t的概率密度函数。
假设w~N(0,σ2I4×4),其中I4×4是维数为4×4的单位矩阵,因此p(u;t)可表示为
(22)
为了简化p(u;t),基于式(6)、式(7)和式(22),对p(u;t)取对数后得到


(23)
接下来将式(23)代入式(21),进一步计算可得I(t)为
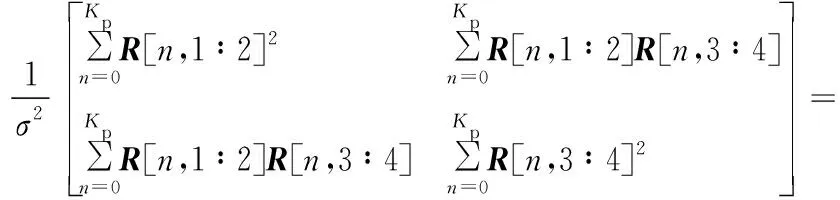
(24)
对式(24)中的矩阵I(t)求逆可得
(25)
基于式(19),由式(25)可得信道h和g的CRLB为
(26)
(27)
4 仿真分析
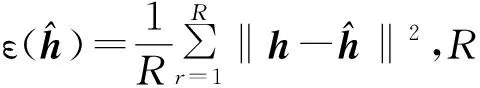
4.1 导频设计对估计性能的影响
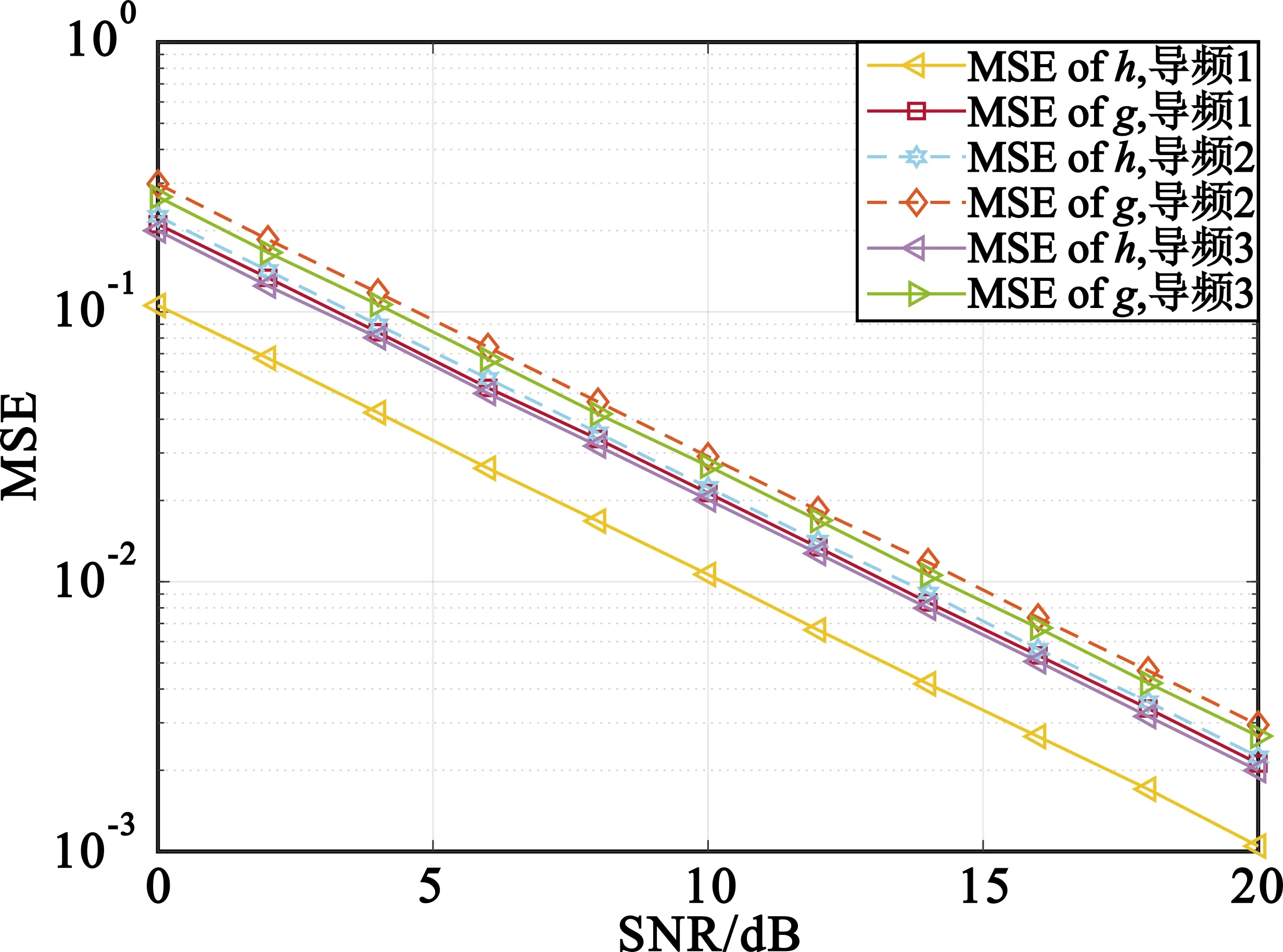
图2为LS算法下三种不同的导频序列对MSE的影响,这三种导频分别是,导频1:随机生成+1和-1的序列,即(2×rand([0 1],Kp,1)-1);导频2:随机生成指数序列,即exp(-1i×2×π×rand(Kp,1));导频3:生成正交导频序列由DFT矩阵获得。图2(a)和(b)仅K0取值不同,Kp相同,均为40。联合观察图2(a)和图(b)发现,当K0=10或K0=20时,三种导频序列的MSE估计性能接近,但是由从图2(a)可以明显发现,当采用导频1时,信道h和g的MSE估计性能是最好的。因此,在接下来的仿真实验中均采用导频1来评价不同算法的MSE性能。
(a)K0=10
图3仿真了K0固定、总导频长度Kp变化下LS算法的MSE性能,设置信噪比(Signal-to-Noise Ratio,SNR)为15 dB。从图中可以看出,K0固定的情况下,信道h的MSE不受总导频长度变化的影响,呈现一条直线。不过,由于Kp的增加使得K1增加,反射信道g的MSE逐渐减小。当Kp=60时,信道g在K0=30时的MSE低于K0=45时的MSE,这是因为K0=45时对应的导频长度K1太短(为Kp的1/4),导致g的估计误差变大。然而,当Kp≥90时,信道g在K0=45时的MSE高于K0=30时的MSE,原因是导频长度K1大于Kp的1/2。此时,继续增加Kp对信道g的误差性能提升很小。总体而言,无论导频多长,信道g的估计总比信道h的估计性能差一些,这是由于前者的估计受后者的估计误差影响。
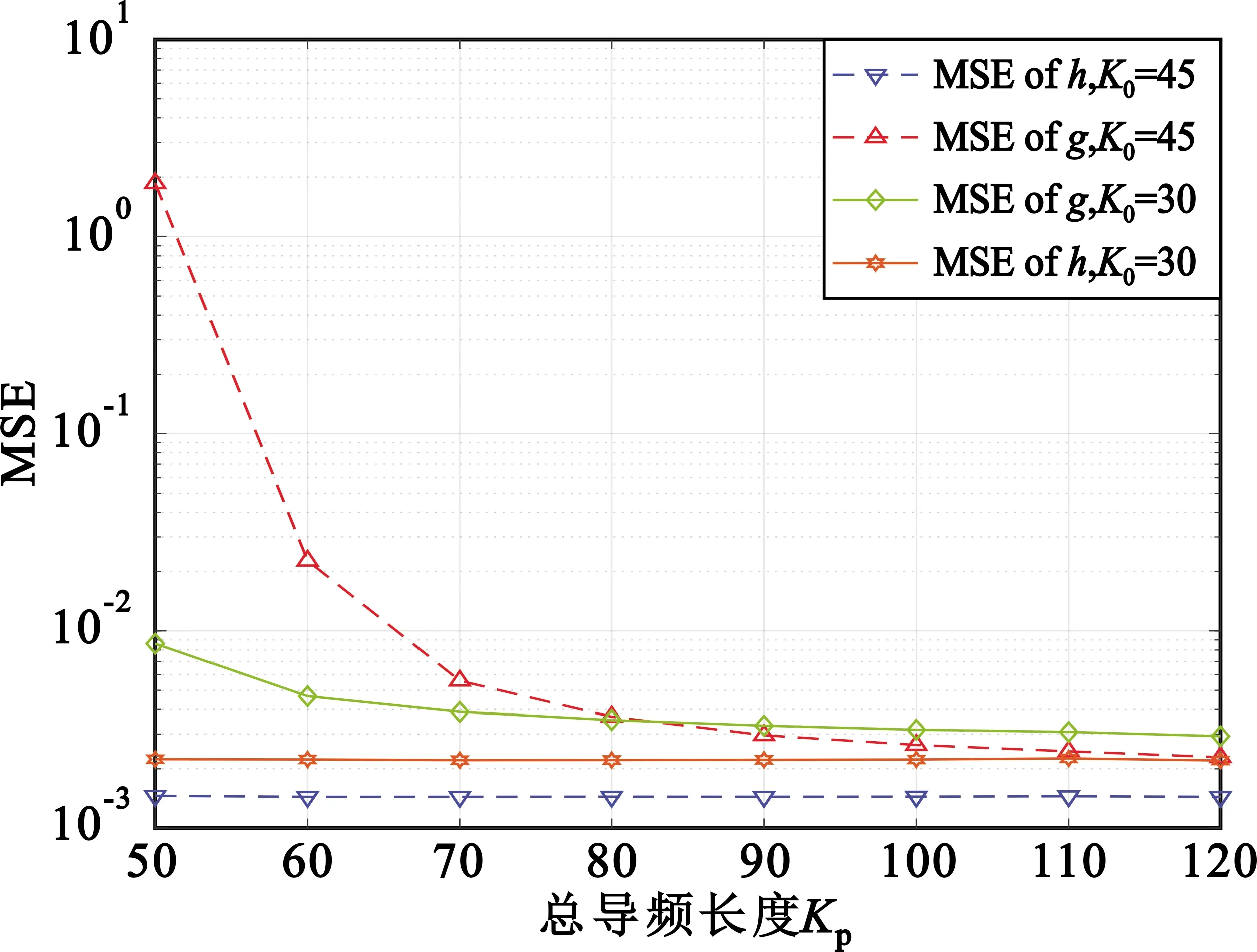
图3 LS算法下Kp对MSE的影响
图4在总导频长度Kp固定的条件下,通过改变K0来观察MSE的变化。此场景的参数为Kp=80。由图可见,当K0≤40时,直接链路h的MSE和反射信道g的MSE都在逐渐减小;然而,随着K0的增加,信道g的性能变差,这是由于K1长度不够造成的(K0>40使得K1小于总导频长度的一半)。显然,SNR较高时,h和g的估计精度都明显提高。
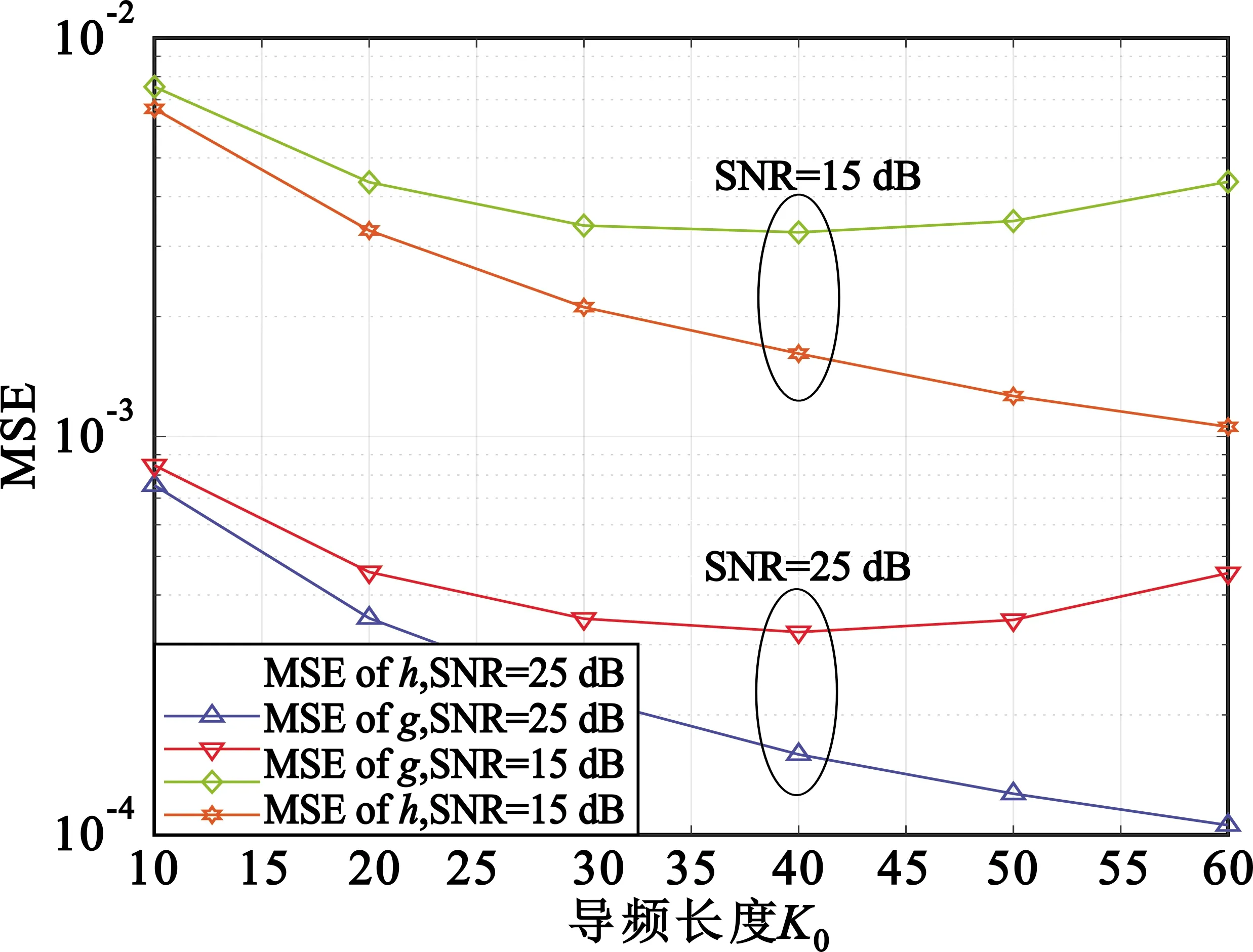
图4 LS算法下K0对MSE的影响
4.2 算法性能对比
本小节仿真对比LS算法和迭代的GS算法的MSE性能,设K0=K1=20。图5显示了LS算法下信道h和g随SNR变化的MSE性能,并根据式(26)和式(27)获得相对应的CRLB。由图可知,随着SNR的增加,h和g的MSE均呈下降趋势;当SNR较高时,估计误差和CRLB之间的差距减小。

图5 LS算法下MSE和CRLB的估计
图6显示了LS算法和GS迭代算法的MSE估计性能的对比结果。从图中可以明显看出,LS算法和GS算法的MSE曲线几乎完全重合,GS迭代算法只需要迭代4次就可以实现与LS算法相同的估计误差性能,因此GS算法实现了更好的性能与复杂度的折中。
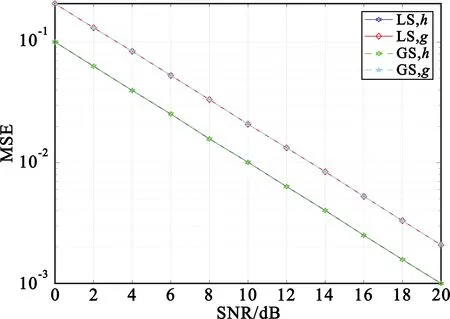
图6 LS估计和GS估计的MSE对比
图7为不同天线数M下GS算法的MSE性能仿真结果。从图中可以明显看出,当天线数增加时,M=4时的MSE要比M=2时的大。这是由于当天线数增加时,需要估计的信道参数以及同信道干扰增加导致估计误差变大。

图7 GS算法下不同天线数的MSE对比
5 结 论
本文研究了下行链路IRS辅助多天线系统的信道估计问题,利用迭代GS算法取代直接的矩阵求逆对直接信道和IRS反射信道进行估计。为了计算理论上的最佳估计精度,进行了CRLB的推导。实验仿真结果表明,为了获得良好的估计性能并降低复杂度,应选择合适的导频序列。信道估计的两个阶段对应的不同导频序列长度对MSE性能有一定的影响,在总长度固定的情况下,应考虑合理分配。GS迭代算法享有低复杂度优势的同时,可达到与LS算法相同的误差性能。

