公路特大桥施工中三角高程进行三等水准测量方法的应用
张怀亮
(中铁十六局集团第五工程有限公司,河北 唐山 064000)
0 引言
目前, 我国重点工程项目对高程精度的要求越来越高,在公路特大桥施工过程中,一般要求三等, 传统的高程测量方法是水准测量和三角高程测量。 这两种方法虽然各有特色, 但都存在着不足。 水准测量是一种直接测高法,但水准测量受地形起伏的限制,使得测站增多,误差积累也增加,当桥梁梁板架通时,水准线路长度减小,其高程精度很难达到三等要求。 三角高程测量是一种间接测高法, 它不受地形起伏的限制, 且施测速度较快。 但精度较低,且每次测量都得量取仪器高和棱镜高。 计算时还得考虑球气差和竖盘指标差的影响,不但麻烦而且增加了误差来源[1]。 尤其在地形起伏较大的山区,采用水准测量方法,不但工作量大,而且测站数太多,若以水准线路长度作为限差计算条件,则很难达到三等精度要求。 使用传统的三角高程测量方法, 由于测量距离远, 误差来源多,大大降低了测量的精度,显示了它的局限性。经过长期摸索, 总结出一种新的三角高程测量方法。这种方法既结合了水准测量的任意置站的特点,又减少了三角高程的误差来源,同时每次测量时还不必量取仪器高、棱镜高,而且不用考虑球气差和竖盘指标差的影响,使三角高程测量精度得到进一步提高,施测速度更快,计算更加简单[2]。
1 三角高程测量的传统方法及计算理论
如图1 所示, 设A、B 为地面上高度不同的两点。 已知A 点高程HA, A、B 两点的高差hAB,即可由HB=HA+hAB得出B 点的高程HB。 由此看出,若要测得B 点高程,必先测出两点间高差。
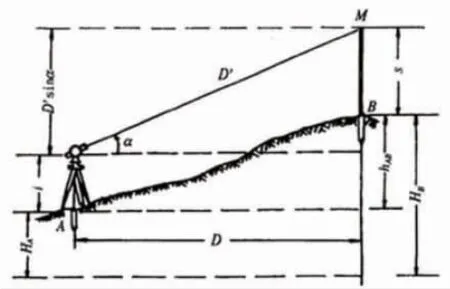
图1 三角高程测量
将全站仪架设在A 点,仪器高为i,反射棱镜架设在B 点,镜高为s,测出视线与水平线之间的夹角,即:竖角α,若A、B 两点的水平距离为D,由三角函数关系可得高差的基本公式如式(1)所示。

在全站仪观测时, 直接读取的是竖盘读数θ,其水平方向一般为90 °(正镜), 存在三角函数关系,因此,高差计算可转换为

竖角计算受竖盘指标差影响,用x 代表竖盘指标差、θ 代表度盘读数,那么竖角计算方法如下

高差的计算还应考虑地球曲率和大气折光影响, 地球曲率对高差影响的改正值通常用公式p=来计算,其中R 为地球半径,一般取地球平均半径6 371 km; 大气折光对高差影响的改正值通常用公式来计算,其中k 为为大气折光系数。此两项合称球气差改正值,计算式为f=p-r=(1-K)。
A、B 两点高差的精密计算如式(2)所示。

从公式(2)中可以看出,影响三角高程精度的因素除了测距误差和竖盘读数误差外, 还存在以下四项误差来源:
(1)指标差测定误差。
(2)仪器高量测误差。
(3)棱镜高量测误差。
(4)球气差改正值中的大气折光系数k 值误差。
这四项误差实际上难以准确测定,若要消除此四项误差就必须寻求新的测量方案——对边测量法。
2 对边测量方法及理论
这种方法就是将全站仪架设于A、B 两点中间的O 点上,A 点为后视点,B 点为前视点,前后视距D 尽量相等,采用正倒镜法观测,前后点采用同一厂家同一型号的一对棱镜和对中杆, 使得前后棱镜高i 相同。这种测量方法的优点在于能够消除指标差、仪器高、棱镜高、球气差等误差。
2.1 竖盘指标差误差的消除
在三角高程测量过程中,采用正倒镜法观测能够消除竖盘指标差误差。 分析如下:
盘左观测时,考虑指标差的影响,竖角计算如式(3)所示。

盘右观测时,考虑指标差的影响,竖角计算如式(4)所示。

一测回竖角值为盘左、盘右竖角的均值,计算如式(5)所示。
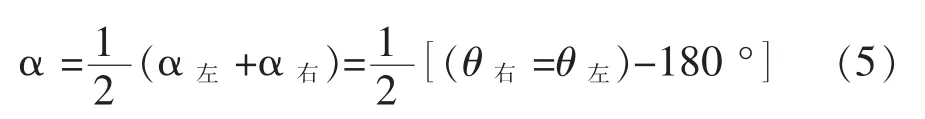
这样就消除了竖盘指标差对三角高程测量的影响。
2.2 仪器高、棱镜高量测误差的消除
在对边测量方法中,前后视的棱镜高相等,都用s表示,这样就可以直接消除仪器高、棱镜高,因此就不存在仪器高、棱镜高的量测误差。 为阐述清晰、直观,暂时不考虑其他误差的影响, 计算O 点到A 点的高差, 根据三角高程的基本计算公式(1), 得hOA=DAO×tgαOA+i-s,A 点到O 点的高差hOA=-hOA,即:
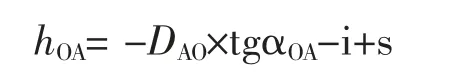
同样计算O 点到B 点的高差为:

A、B 两点的高差hAB,就是A 点到O 点的高差hAO与O 点到B 点的高差hOB之和,计算如式(6)所示。

从公式(6)中可以看出,A、B 两点的高差与仪器高、棱镜高没有关系,因此也就不需要量测仪器高、棱镜高了。
2.3 球气差改正值的消除或削弱
两点高差的精密计算如式(7)所示。
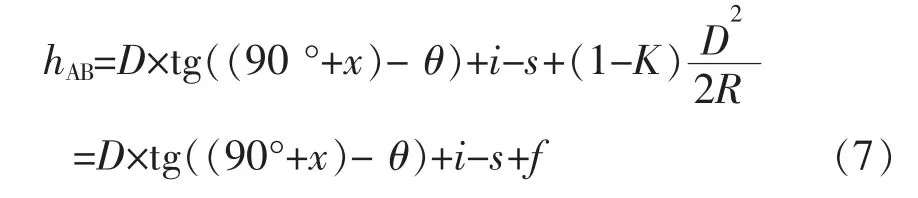
为阐述清晰、直观,暂时不考虑其他误差的影响,且指标差、仪器高、棱镜高已被消除,公式可转化为式(8):

这个公式表述的意义实际上是A 点的仪器中心到B 点棱镜中心的高差。
计算O 点到A 点的高差, 根据公式 (8),得hOA= DAO×tgαOA+f, A 点到O 点的高差hAO=-hOA,即:

同样计算O 点到B 点的高差为:

A、B 两点的高差hAB,就是A 点到O 点的高差hAO与O 点到B 点的高差hOB之和,计算如式(9)所示。

从公式(9)中可以看出,A、B 两点的高差与球气差没有关系,或者说关系不大,可以忽略不计。用全站仪观测两点高差的距离,一般不超过1 000 m(如果两点之间距离过长,则应加设转点),当前后视距差为15 m 时, 设AO 的距离为520 m,OB 的距离为505 m,经计算,两段球气差改正值之差为仅为1.01 mm。 所以,值得注意的是:采用这种方法应尽量使前后视距离相近,视距差不能超过15 m,前后视距离也不要过长,一般在300 m 左右为宜。
现在的全站仪能够直接测出两点间的高差,在不考虑仪器高、棱镜高、球气差等误差因素时,在仪器内将仪器高、棱镜高设为0 m,计算A、B 两点高差时直接采用公式hAB=hAO+hOB=hOB-hOA,既方便又快捷。
3 对边测量在工程中的应用
十堰至天水高速公路白水河特大桥,桥长812 m,按《工程测量规范》规定,水准等级为三等。 本桥附近有3 个控制点,分别为LJ33、LJ34、LJ35。 采用三角高程测量法 (对边测量) 观测, 自LJ33 测至LJ35,为保证测量精度,又从LJ35 号点经临时点A测至LJ33 号点,形成闭合水准线路。 表中C1、C2、C3、C4 为仪器测站编号,每测站施测三测回,具体观测值见表1。

表1 观测值
由表1 可见,采用三角高程测量方法(对边测量法)能够满足三等水准测量精度要求。
4 结语
随着科学技术的发展,全站仪的自动照准功能的开发,使全站仪的捕捉功能越来越精确,三角高程对边测量法也有了更大的发展空间和推广使用价值。

