面向抛磨机器人的高精度力控装置设计与分析*
熊次远,杨桂林,刘立涛 ,冯 凯 ,陈庆盈 ,张国龙,3
(1.中国科学院宁波材料技术与工程研究所,宁波 315201;2.浙江省机器人与智能制造装备技术重点实验室,宁波 315201;3.宁波大学科学技术学院,宁波 315300)
0 引言
抛磨作为零件加工过程的重要工序,其加工质量对工件的耐蚀性、耐磨性、疲劳强度等有重大影响[1]。传统的抛磨依靠人工操作,效率低,环境差,一致性差[2]。近年来,采用工业机器人进行抛磨成为趋势,机器人抛磨属于连续接触式作业,需要精确控制抛磨过程中的压力[3-5]。机器人进行力控制的方法[6]主要有两种:一种是通过控制机器人关节的力矩实现力控制,该方法需对机器人建立准确的动力学模型以及开发相应的控制算法,而由于传统的工业机器人自重大、惯量大,受机器人惯性冲击影响,力控精度低;另一种是在机械臂末端安装额外的力控装置,由机器人实现运动控制,力控装置实现力控制,该方法动态响应好、通用性好,成为机器人力控的主流方式。
按照自由度不同力控装置分为单自由度和多自由度两类。多自由度力控装置灵活性好,但是结构复杂、质量大、成本高,目前市场上还没有成熟的产品。单自由度力控装置以结构简单、质量轻、成本低等优势成为市场的主导产品。国外已经商业化的产品有美国生产的AFD系列[7]和奥地利生产的FerRobotics系列[8]力控装置,其都属于气动式。针对气动式力控装置存在响应速度慢、力控精度低的共性问题,团队创新性提出了气电混合式力控装置设计方案,并设计出几种力控装置样机[9-10],兼具柔性好、缓冲能力强、响应快、精度高等特点。但是由于都是采用气囊作为气动组件,而气囊输出力较大、外形尺寸大且随位移变化输出力变化较大,导致力控装置存在结构不够紧凑、响应速度不够快等问题。
本文针对传统气动式力控装置存在力控精度低、响应慢的问题,提出了一种基于音圈电机和氮气弹簧并联输出的高精度力控装置设计方案。通过将高精度的音圈电机和输出力相对恒定的氮气弹簧并联输出的方式,使之在具备高力控精度和高响应速度的同时还具备良好的缓冲性能;通过引入拉伸弹簧,并将氮气弹簧安装于中空音圈电机内部,使力控装置结构紧凑,并进一步提高其响应速度和力控带宽。对其输出力特性进行分析研究,有助于实现工件抛磨接触力的精密控制。
1 系统设计
1.1 方案设计
基于音圈电机直驱的高精度末端力控装置设计方案如图1所示。

图1 力控装置设计方案图
其中定平台固定于机械臂末端,在定平台和动平台之间并联设置有音圈电机和氮气弹簧,音圈电机定子和定平台直接连接,动子和动平台直接连接;将音圈电机设计成中空结构,并将氮气弹簧同心设置于其内部,使其结构非常紧凑;进一步地,在定平台和动平台之间还并联了多根拉伸弹簧,以提高响应速度和力控带宽。动平台和抛光工具之间设有力传感器用于检测抛光过程的实际接触力。
1.2 结构设计及有限元分析
基于音圈电机直驱的高精度末端力控装置的结构如图2所示,主要由音圈电机、氮气弹簧、拉伸弹簧、动平台、定平台、固定外套、活动内套、导向装置、光栅位移传感器等组成。其中氮气弹簧、中空音圈电机、活动内套和固定外套依次从内到外同轴心布置。固定外套、音圈电机定子、氮气弹簧缸体直接或间接与定平台固定连接,组成固定组件;活动内套、音圈电机动子、氮气弹簧活塞杆直接或间接与动平台固定连接,组成活动组件。活动组件和固定组件之间通过导向装置导向,导向装置由沿周向均布的三根双滑块精密直线滑轨组成,滑轨和活动内套连接,滑块和固定外套连接,从而使其具备承受较大侧向负载的能力。在音圈电机、氮气弹簧和拉伸弹簧的共同作用下,活动组件沿着导向装置可往复运动,其行程由限位块限制。位移传感器包括高精度光栅尺和光栅读头。

图2 力控装置结构图
机器人抛磨加工时,力控装置除了受到抛光压力外,还受到由于摩擦产生的侧向力,其大小和抛光压力成正比,力控装置侧向刚度对其导向和力控精度有重要影响。采用有限元分析方法,对结构模型进行简化处理,保留主要结构尺寸,设置材料类型为铝合金,进行四面体网格划分,在定平台上表面添加固定约束,在动平台侧面施加150 N集中力,力控装置在最大行程位置时,应力和位移云图如图3和图4所示。从中可知最大应力仅约为5.8 MPa,最大位移只有0.005 2 mm,该力控装置强度符合设计要求,具有较大的结构刚度,有利于提高力控精度。
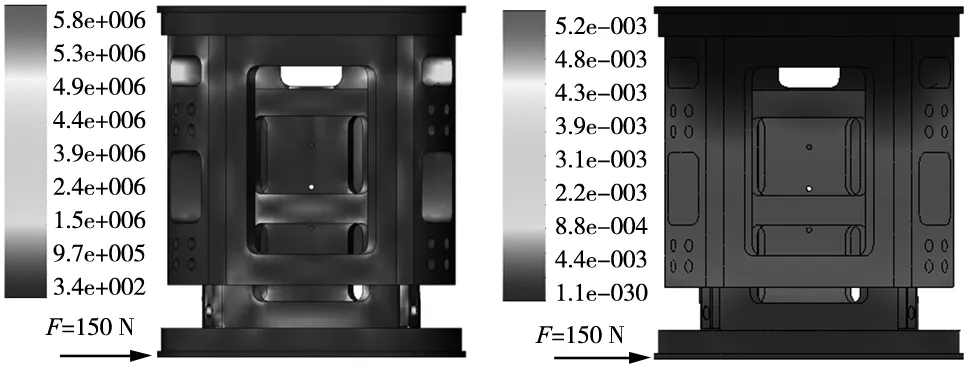
图3 应力云图 图4 位移云图
2 系统性能分析
影响系统输出力的组件有氮气弹簧、音圈电机和拉伸弹簧,分别对其输出力特性进行分析研究。
2.1 氮气弹簧输出力分析
氮气弹簧内部结构如图5所示,其压缩过程可认定为等温过程[11],根据气体状态方程有:
P0V0=PxVx
(1)
式中,P0为初始状态压强;V0为初始状态体积;Px为压缩量x时压强;Vx为压缩量x时体积。

图5 氮气弹簧内部结构简图
当氮气弹簧压缩位移x时,其体积计算公式为:
Vx=V0-πd2x/4
(2)
联立式(1)和式(2)可得氮气弹簧压强和位移的关系:
(3)
进一步地,得出氮气弹簧弹力和位移的关系:
(4)
式中,F0为初始状态弹力;Fx为压缩量x时弹力。
由式(4)可知,通过改变结构参数和初始压强,可使氮气弹簧具有较小的弹簧刚度。通过将位移分段,如图6所示,在小段位移范围内可以近似用线性关系来替代。所选氮气弹簧行程为40 mm,通过限位使其位移在10~30 mm变化,并用线性关系来替代,故氮气弹簧弹力和位移可简化为:
(5)
式中,F1为氮气弹簧压缩位移10 mm时的弹力;F2为氮气弹簧压缩位移30 mm时的弹力;10 mm≤x≤30 mm。

图6 氮气弹簧弹力和位移特性曲线
2.2 音圈电机输出力分析
音圈电机主要包括永磁体定子和线圈动子两部分,将音圈电机设计成空心结构以便将氮气弹簧设置于其内部,中空音圈电机结构如图7a所示,其输出力与线圈中电流成正比,计算公式如下:
Fe=nBLi=kei
(6)
式中,ke=nBL为力常数;n为线圈匝数;B为磁场强度;L为每匝线圈的长度;i为线圈中电流。
音圈电机电路模型如图7b所示,根据电压平衡方程得:
(7)
式中,R为电阻;L为电感;Blv为反电动势。此处忽略反电动势的影响,对式(6)和式(7)进行拉普拉斯变换得到音圈电机输出力的传递函数为:
(8)
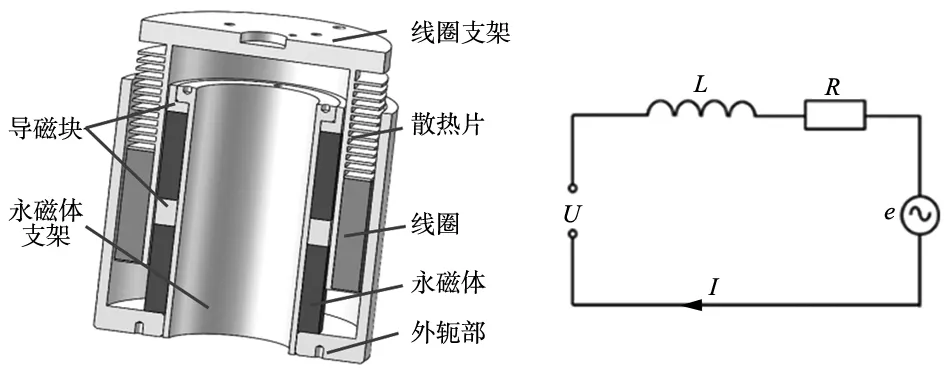
(a) 音圈电机结构图 (b) 音圈电机电路模型
2.3 拉伸弹簧输出力分析
对动平台进行受力分析可知拉伸弹簧拉力始终向上,氮气弹簧弹力始终向下,当力控装置处于缩回位置(行程为0 mm)时,拉伸弹簧拉力最小,氮气弹簧弹力最大,向下的合力最大,此时音圈电机所需的持续输出力最小应等于向下的合力,这样才能保证最小压力为0;当力控装置行程增大时,拉伸弹簧拉力增大,氮气弹簧弹力减小,向下的合力减小;当力控装置处于最长位置(行程为20 mm)时,拉伸弹簧拉力最大,氮气弹簧弹力最小,向下的合力最小,此时音圈电机输出力向下时产生的压力为整个行程内都能够提供的最大压力。
动平台两极限位置受力分析如图8所示。

(a) 最小压力状态 (b) 最大压力状态
根据力平衡方程可得:
FLmin+FY+FJmin=FDmax+mg
(9)
FLmax+FJmax=FDmin+FY+mg
(10)
式中,FLmin和FLmax为拉伸弹簧的最小拉力与最大拉力;FDmin和FDmax为氮气弹簧的最小弹力与最大弹力;FJmin和FJmax为抛光的最小压力与最大压力;FY为音圈电机持续输出力。
由于该装置行程为20 mm,最小压力为0,并且拉伸弹簧和氮气弹簧输出力和位移都是线性关系:
FLmax=FLmin+20kL
(11)
FDmax=FDmin+20kD
(12)
联立式(9)~式(12)可得:
FJmax=2FY-20(kL+kD)
(13)
式中,kL为拉伸弹簧刚度;kD为氮气弹簧刚度。
令120 N≤FJmax≤170 N,将设计的音圈电机持续输出力FY=125 N,选取的氮气弹簧刚度kD=0.3 N/mm,代入式(13)可得:3.7 N/mm≤kL≤6.2 N/mm。
3 系统动力学模型及弹簧刚度优化
3.1 系统动力学模型
该力控装置可等效为如图9所示的弹簧-质量-阻尼系统,由牛顿第二定律得到系统动力学方程为:
(14)
式中,m为运动部分质量;c为阻尼系数;x为位移;FJ为接触力。对式(14)进行拉普拉斯变换得:
(15)
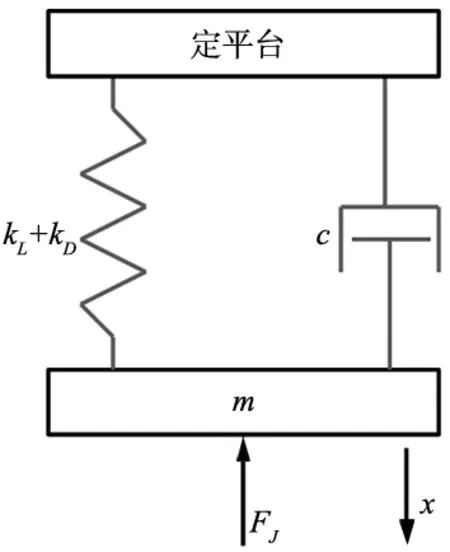
图9 系统等效模型
3.2 拉伸弹簧刚度优化
由式(15)可得系统的特征方程如下:
(16)

从而得到系统的响应时间t和超调量σ如下:
(17)
(18)
将测得参数m=3 kg,c=185 Ns/m代入式(17)、式(18),得到超调量和响应时间随拉伸弹簧刚度的变化情况如图10所示。从图中可知,在拉伸弹簧刚度约束范围内,随着拉伸弹簧刚度的增大,系统的响应时间变小,反之,超调量变大。需对拉伸弹簧的刚度进行优化,通过加权的方式将多目标优化简化为单目标优化问题。
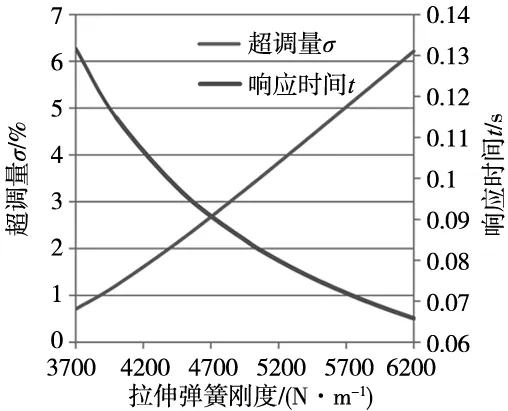
图10 超调量和响应时间随弹簧刚度的变化情况
(1)目标函数。考虑到目标以降低响应时间为主,故将响应时间的权重因子取为0.6,将超调量权重因子取为0.4,然后通过加权得到目标函数为:
Y=0.6t+0.4σ
(19)
(2)约束条件。通过上述对动平台受力分析,得到弹簧刚度的取值范围为:3.7 N/mm≤kL≤6.2 N/mm。
(3)优化算法。遗传算法是一种常用的全局最优解算法,选用遗传算法对系统进行优化求解。
(4)优化结果。优化结果如图11所示,优化前后主要参数如表1所示。当拉伸弹簧刚度为5445 N/m时目标函数收敛,优化后超调量由0.71%增加到4.2%,但响应时间由132 ms降低到75 ms,综合考虑优化结果有效。
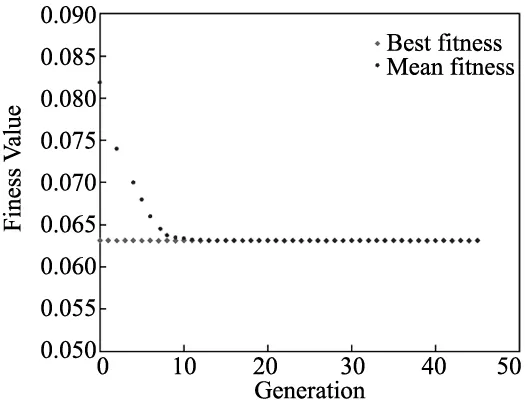
图11 优化结果

表1 优化前后主要参数
4 样机研制及实验验证
研制的基于音圈电机直驱的高精度末端力控装置样机如图12所示,该样机及其主要组成组件参数如表2和表3所示,基于该力控装置搭建的抛磨机器人实验系统如图13所示。利用该实验系统对汽车轮毂进行抛磨实验,以验证该力控装置的力控性能。

表2 样机结构参数

表3 主要组成组件参数

图12 力控装置样机图13 基于新设计力控装 置的抛磨实验系统
为了测试该力控装置的响应时间和力控精度,进行阶跃力和恒力跟踪实验。采用直接力控算法,由力传感器实时检测并回馈实际抛磨压力,并根据实际力与期望力的力偏差信号控制音圈电机的电流大小实现抛磨压力的精确控制,其控制原理图如图14所示。其中,Fr为期望力;Fc为实际力;e1为力偏差;e2为电流偏差;id为电流环输入;i为电流输出;ig为重力补偿电流;FY为音圈电机输出力;FL为拉伸弹簧输出力;FD为氮气弹簧输出力。
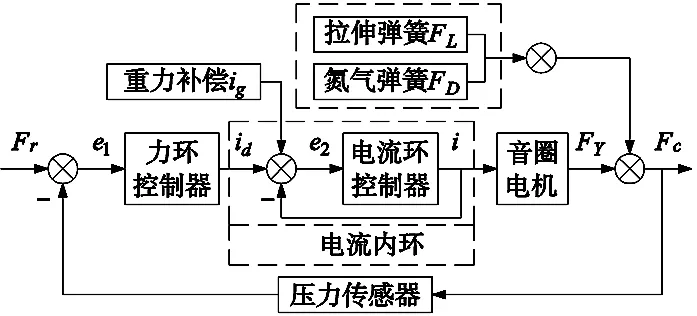
图14 直接力控原理图
在该系统中,力环和电流环均采用PID控制器, 设置期望抛磨接触力先由5 N突变为10 N,然后恒定在10 N,实验结果如图15和图16所示。
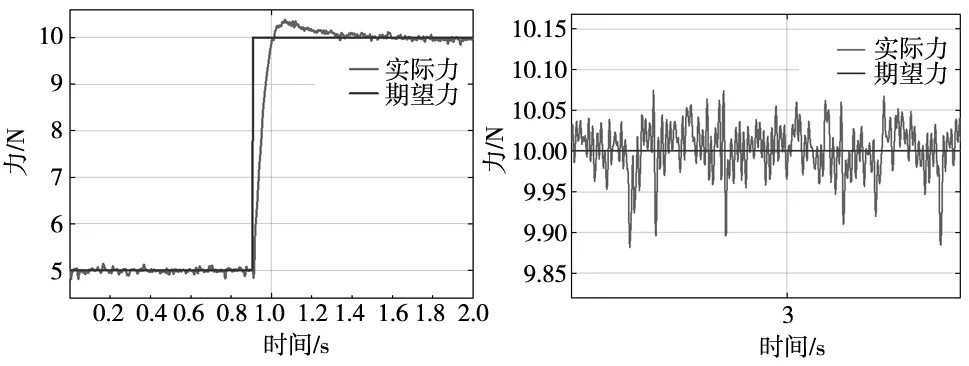
图15 阶跃力跟踪实验结果 图16 恒力跟踪实验结果
由图15可知,接触力从5 N突变到10 N的过程中,该力控装置的响应时间小于0.1 s,过程中出现了短暂的超调现象,之后迅速稳定下来。
由图16可知,该力控装置的力控制精度为±0.1 N,其响应时间和力控精度均优于传统的力控装置。
5 结论
本文提出了一种基于音圈电机直驱的高精度力控装置设计方案,并通过将氮气弹簧和音圈电机并联,使之在具备高力控精度和高响应速度的同时还具备良好的缓冲性能;通过引入拉伸弹簧,进一步提高了系统的响应速度和力控带宽。分别对氮气弹簧、音圈电机、拉伸弹簧的输出力特性进行分析研究,并对拉伸弹簧的刚度进行了优化。基于优化结果研制出力控装置样机并进行机器人抛磨实验,实验结果显示该力控装置基于音圈电机的快速响应和高精度的特性其阶跃力跟踪响应时间小于0.1 s,力控制精度为±0.1 N,其力控性能明显优于传统的力控装置。该力控装置兼具有缓冲性能好、结构紧凑、力控范围大、带宽大、质量小等多种优点,在机器人连续接触式加工领域具有非常广阔的应用前景。

