面向电力消费量的多因素插值算法研究

李道强,汪涛,申少辉,徐俊

（1.浙江电力交易中心有限公司，浙江杭州 310000；2.北京科东电力控制系统有限责任公司，北京 100194）

1 引言

由于我国电网管理日趋现代化，电力数据日益完善和丰富，为研究电力市场运营规律提供了更加完善详实的基础。但由于电力信息平台发展不完善，和早期数据不完备，以及电力数据因来源不同而造成数据分布不规则，数据缺失等各种问题，给数据的获取和使用带来不便[1]。此外，在数据查询、插值或完善时，还涉及不同影响因素的作业存在差异，即灵敏度不同，为此本文以电力能源供给为例，探索适应新一代电力信息平台的数据查询插值算法及工具。

现货电力供给包括火力、水利、风力、太阳能等多方面来源，其变化受煤炭和石油价格、降水、气温、光照、国家政策和投资等多方面因素影响，很难做到不同因素组合下的数据齐全，属于多维不完备数据，给数据规律的查询、使用和规律研究带来困难，为此本文针对电力市场特点构建查询和插值算法，为电力数据的研究提供基础。

目前常用的多维插值算法有双线性插值、反距离加权插值、克里金插值法等。这些算法应用在很多的领域，如图像处理领域[2-3]；气象空间领域[4-5]；土地资源领域[6-7]。其中图像处理领域包括医学图像分析；卫星遥感图像分析；军事雷达图像分析和天文观测图像分析。本文针对现货电力市场数据多因素、多尺度等特点，尝试三因素的四面体插值、加权邻域插值，并使用Fortran95 语言开发相关程序，分析它们特点和效果。

2 加权邻域插值

邻域插值算法是基于反距离加权法的简化算法，其把对插值点有影响的点限制在一定的邻域内，只认为在此邻域内的点才有意义。对于电力数据，因为各个因素量级不同，所以作用差异明显，这种算法难以直接使用。为此，本文对其进行改造，建立如下加权邻域插值算法。

设某关心指标y，如某时的电量供给量，数据库中对应该指标的n 个影响因素为xi(i=1，2，…，n)，构造如下多维插值算法。

1)设目标值为y(j)某数据点j，其坐标为x(i)i(i=1，2，…，n)，采用向量2 范数定义该点到目标点ai(i=1，2，…，n)点加权距离平方为：

2)对应目标点内的m 个参考数据，计算每个离散点对目标值所占的权重为：

其中，wi(i=1，2，…，n)为各个因素的权函数，并与该因素的尺度、对电力目标值灵敏度有关，在实际使用中可针对各个因素进行选择确定。

3)以hi作为m 个离散点权重系数得出最终插值计算公式为：

其中，y即为所需要提取的电力信息目标值。

加权邻域插值算法考虑了邻域内数据点对目标插值点的影响，当邻域范围较小时，邻域数量个数可能较少，数据可能会出现不够准确或失真现象；当邻域范围较大时，则会因数据量大，局部变化规律被淡化现象。在实际使用时，可通过给定参考数据个数，构建变化和自适应的邻域范围来实现查询和插值。本算法的程序流程图如图1所示。

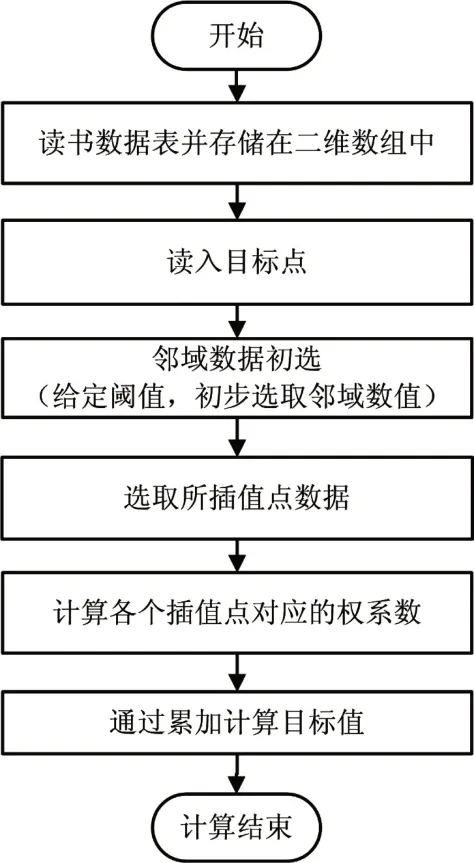
图1 邻域插值算法程序设计流程

3 三因素四面体算法

电力数据往往影响因素较多，比如某地区电力消费量会随着气温、当地生产活跃度、时间段不同而变化，为了探求适应性更强的数据查询和插值方法，这里借鉴有限元法的思路，给出三因素四面体单元插值算法。可以适应各种数据分布情况。

实现插值算法时，可搜索目标点最近的四个数据点，三指标构成的三维空间中，会形成一个四面体，再进一步构造如下四面体的插值函数。

设电力指标量在四面体各顶点的值分别fi(i=1，2，3，4)，则该指标场量可以按照如下插值函数计算：

式中：Li(i=1，2，3，4)为各顶点在四面体（图2)上的体积坐标。

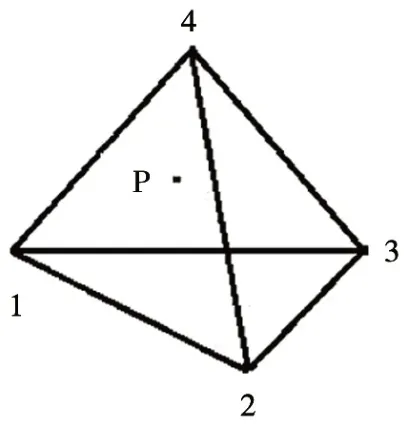
图2 三因素四面体

设插值目标点为P，并设各矢量P1、P2、P3、P4分别为矢量则各部分的体积分别为：

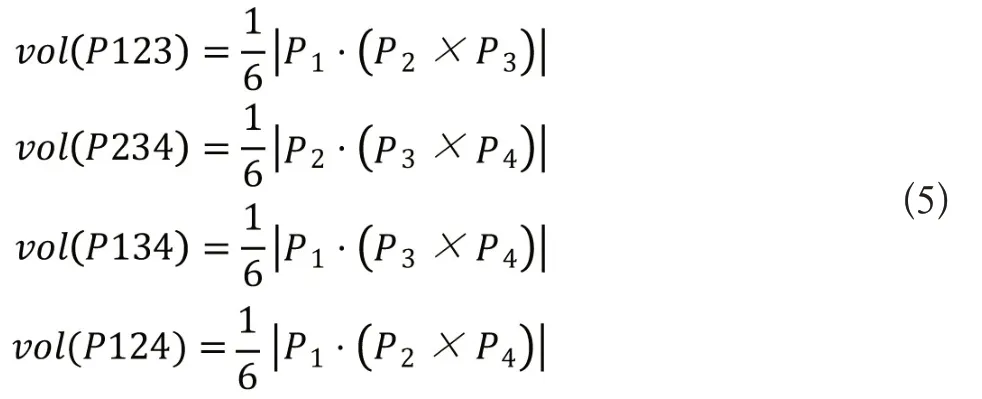
同时，

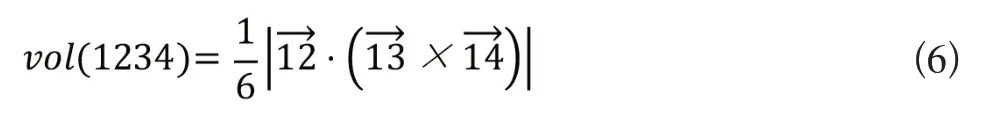
则各体积坐标可表达为：

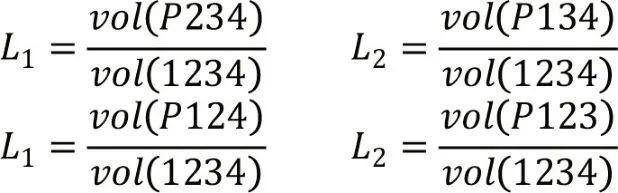
4 插值算法精度比较

利用以上三种插值算法，对某地区近几年最大用电负荷（见表1)进行查询研究，为了验证算法，删除表中个别数据，并采用文中给出算法进行查询预测测试研究。这里依次将各个数据点作为查询目标点，三种算法的误差统计如表2所示。

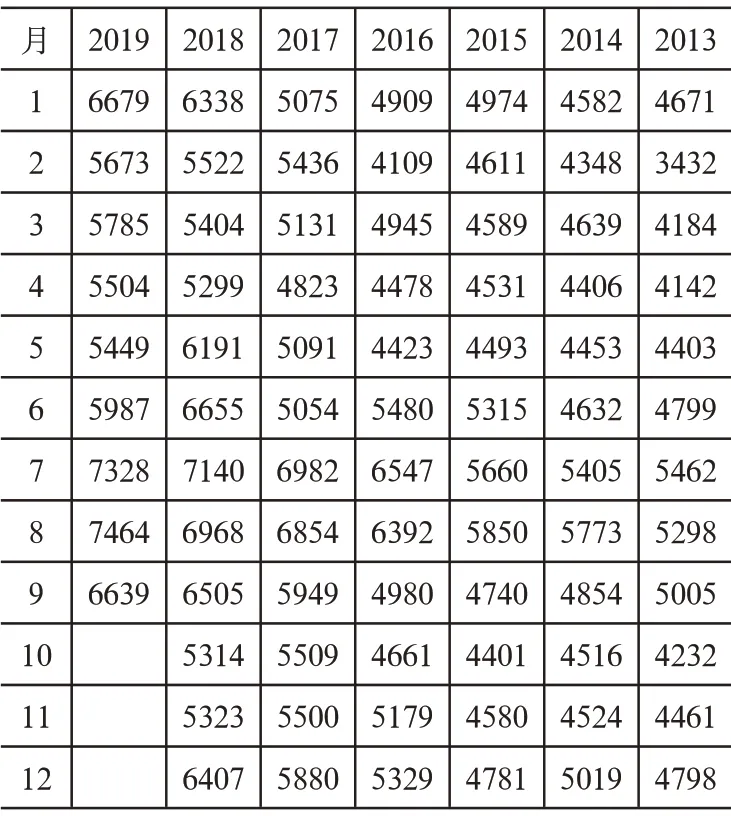
表1 某地区电力消费量(万千瓦时)

由表2可以看出，对于不规则分布的离散数据，邻域插值算法误差较大，四面体插值算法误差很小。

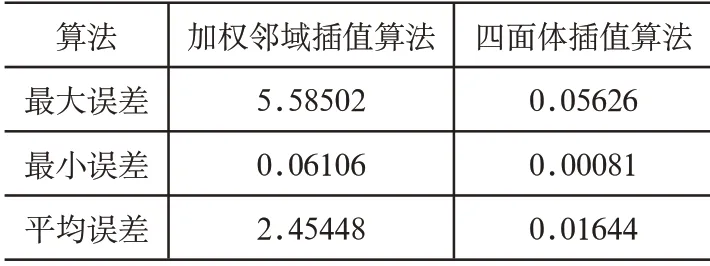
表2 误差统计(%)

5 结束语

本文针对电力信息平台融合中的电力数据缺失等问题，给出了两种插值提取方法。总结如下：

（1)两种算法均具有较强的适应性，对应数据分布没有严格要求；

（2)加权邻域插值算法可以适应各种因素个数情况下的数据提取，其算法精度受到提取目标点与临近数据距离，以及因素对目标值的敏感度影响较大；

（3)经过对比，发现四面体插值算法具有比较高的效率和精度，非常适合不规则分布电力数据的特点。