基于DEA算法的矿山修复生态效益评估模型

谷丛楠

（天津市地质研究和海洋地质中心，天津市河东区 300000）

0 引言

矿山生态修复包括污染废弃地以及未污染而被挖损和压占的土地，20世纪，随着社会经济的不断发展，矿产资源被大量开采挖掘，资源遭到破坏[1～2]。其中，最为严重的为植被破坏和水源污染。植被破坏会导致滑坡、山洪、塌陷等事故发生，水源污染会导致周边居民患病，如痢疾、霍乱和伤寒等，面对此类矿山，对其展开矿山生态修复现已成为重要的环境治理议题[3～4]。张雪松等[5]认为CW-GRAP模型对随州市土地整治综合效益评价具有重要意义，罗明等[6]认为粤北南岭典型矿山生态修复工程技术模式与效益预评估具有重要意义，上述两种模型完成了矿山修复生态效益评估，但修复生态效益评估均存在不同程度评估偏差，且稳定性能较差。

数据包络分析方法(Data Envelopment Analysis,DEA)是运筹学、管理科学与数理经济学交叉研究的一个新领域。它是根据多项投入指标和多项产出指标，利用线性规划的方法，对具有可比性的同类型单位进行相对有效性评价的一种数量分析方法。DEA算法在评估输出高于输入的有效性评估方面具有绝对优势，且无需对数据实施量化处理和权重假设，评估结果较为精确。因此，本文构建基于DEA算法的矿山修复生态效益评估模型，采用层次分析法建立矿山修复生态效益评估指标体系，获取一级、二级和三级评估指标，通过DEA算法构建矿山修复生态效益评估模型，以完善实际生态效益评估过程中存在的缺点，为矿山未来发展规划提供参考依据。

1 矿山修复生态效益评估模型

1.1 矿山修复生态效益评估指标体系建立

在进行第一轮矿山修复生态效益评估指标选取时，该指标需具有客观性、独立性、系统性等特点，由于所选取的矿山修复生态效益评估指标要按照矿山地理区域特征和其修复生态效益目的进行合理选取[7]，因此，在第一轮指标选取的基础上进行第二轮指标筛选，且该指标获取的难度一般，可从时间、空间等方面较好地反映该矿山水土生态恢复情况、走向和生态效益恢复布局与结构，并在数量上和层次上充分展示矿山修复生态效益规模与矿山系统功能和水平即可，使最终选取的矿山修复生态效益评估指标具有一定的实用性。依据上述原则所构建的矿山修复生态效益指标体系不仅单个指标可进行延伸，且兼备描述、评价功能。

本文利用层次分析法，建立矿山修复生态效益评估指标体系，并结合专家意见将矿山修复生态效益评估指标体系分为一级、二级和三级3个指标等级，如表1所示。矿山修复生态效益的关键目标是合理反映修复生态效益结果[8]，因此选择土壤、植物和水等作为生态和成本等经济指标，而社会指标则可作为导向指标，生态、经济和社会等三方面作为矿山修复生态效益指标，从矿山修复生态效益指标中能够获取其生态恢复情况[9]。

表1 矿山修复生态效益评估指标体系Table 1.Evaluation index system of ecological benefits of mine restoration

为提升评估结果标准化，并具有较高可比性，利用五级制评分方法对矿山修复生态效益指标进行评分[10]。

1.2 基于DEA算法的矿山修复生态效益评估模型

带有非阿基米德无穷小量ε对第j0个DMU实施评估的DEA模型表达公式如下：

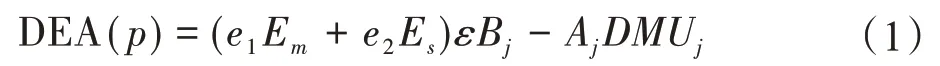
公式（1）中，Aj=(a1j,…,amj)T、Bj=(b1j,…,bsj)T分别表示决策单元j的投入与产出要素集合，(Aj,Bj)表示第j个决策单元DMUj，j=1,…,n，Em表示m维向量空间，Es表示s维向量空间。

将下标设置为0，即Aj0和Bj0可用来表示某个特定的决策单元，利用C2R模型判断该特定的决策单元的有效性[11]，其对偶规划表达公式如下：

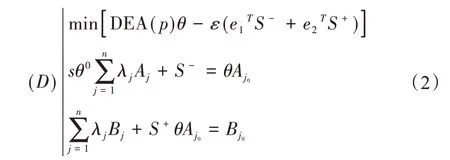
公式（2）中，λj≥0，S-≥0，S+≥0，θ表示决策单元的有效值，θ0为(D)的最优效率评价指数，λj表示对评价比例系数。S-m表示项输入剩余变量，S+表示s项输出松弛变量，其表达公式如下：

对C2R线性规划模型求解，可得θ0、、S0-、S0+数值，并对其进行有效性判定，判定流程如下：

第一步：当θ0=1并满足S0-和S0+分别为0的条件时，则判定第j0个DMU是DEA有效，在由决策单元组成的矿山修复生态效益系统内，原投入基础上的产出达到最优化，表明此时该决策单元同时符合规模和效益的最高标准[12～13]。

第二步：当θ0=1并满足S0-和S0+分别不为0的条件时，则判定第j0个DMU是DEA弱有效，在由决策单元组成的矿山修复生态效益系统内，可在投入a0基础上适当降低S0-或提升S0+，从而保证产出b0不发生变化。

第三步：当θ0＜1，则判定第j0个DMU是DEA无效，其解决办法是适当降低原投入a0和θ0的比例，保证产出b0不变。

第四步：通过(D)的最优解，对第j0个DMU的规模报酬性展开分析判定，令：

当SR＞1时，表示规模报酬递减；当SR=1时，表示规模报酬不会变化；当SR＜1时，表示规模报酬递增[14]。在判定SR时，需在公式（2）内加入以下约束条件：

其中j=1,2,…n。

在分析第j0个DMU时，利用DEA模型对n个评价对象展开有效性判定，并根据最优解对评价对象的相对效率序列进行判定[15]。依据λ可判定形影决策单元内的规模效益变化情况。

当DEA为无效的DMU单元时，可利用投影定理对其进行处理，处理过程如下：

假设决策DMU0单元相对应C2R模型的最优解为θ0、S-、S+，令：

公式（7）中，(a0′,b0′)表示DMU对应的（a0，b0）在DEA相对有效面的投影。依据上述假设条件，相对于原来的n个DMU来说，此时DEA判定为有效。

假设a0′=a0，且b0′=b0，则DMUj0(a0,b0)为DEA有效的充分条件，其表达公式如下：

公式（8）中，Δa0表示输入剩余，Δb0表示输入亏空。

当DEA为无效的DMU单元时，对其进行投影，在保证输出数值一定的情况下，降低原来的输入，或在保证输入数值一定的情况下，提升输出数值，利用该投影方法，可有效判断DEA无效时矿区修复生态效益系统的具体情况。

2 仿真实验分析

为了验证本文设计的基于DEA算法的矿山修复生态效益评估模型在实际应用中的性能，进行一次仿真实验分析。以某地一大型矿区为例，将该矿山分为三个区域，由于该矿山修复生态效益评估所需时间较长，因此选择该矿区最近3年内9862个生态效益数据为评估对象，分别从评估有效性、评估准确性和评估效率以及评估稳定性方面对该矿区生态效益展开评估。由于DEA模型指标不受量纲限制，将矿区修复生态效益输入输出数据设定在[1，100]内，具体数据详见表2。将该矿区生态效益数据输入到C2R模型内展开评估。

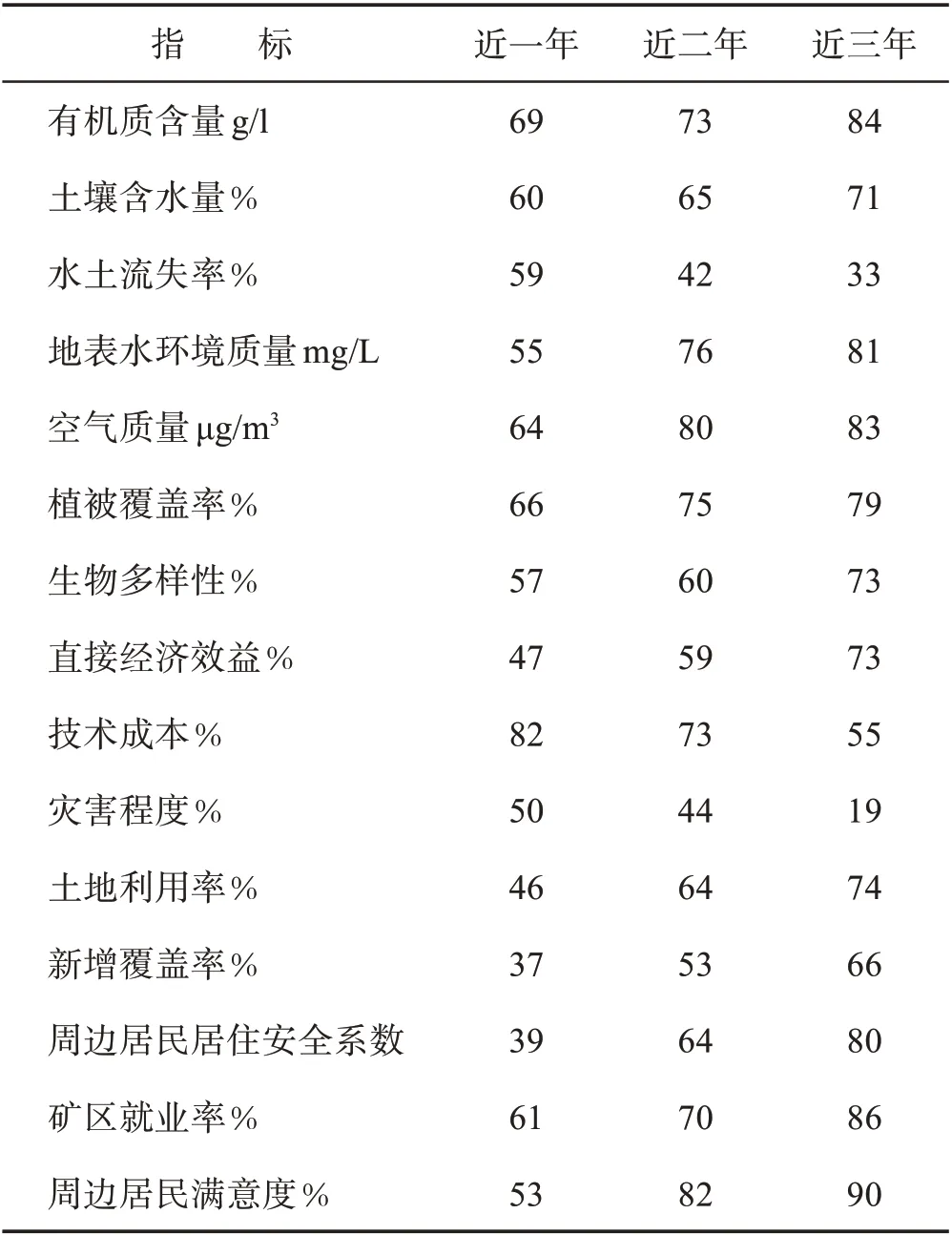
表2 矿区修复生态效益输入输出数据Table 2.Input and output data of ecological benefits of mine restoration

2.1 模型有效性分析

采用专家评分的形式对该矿区生态效益进行评分，评分结果如表3所示。

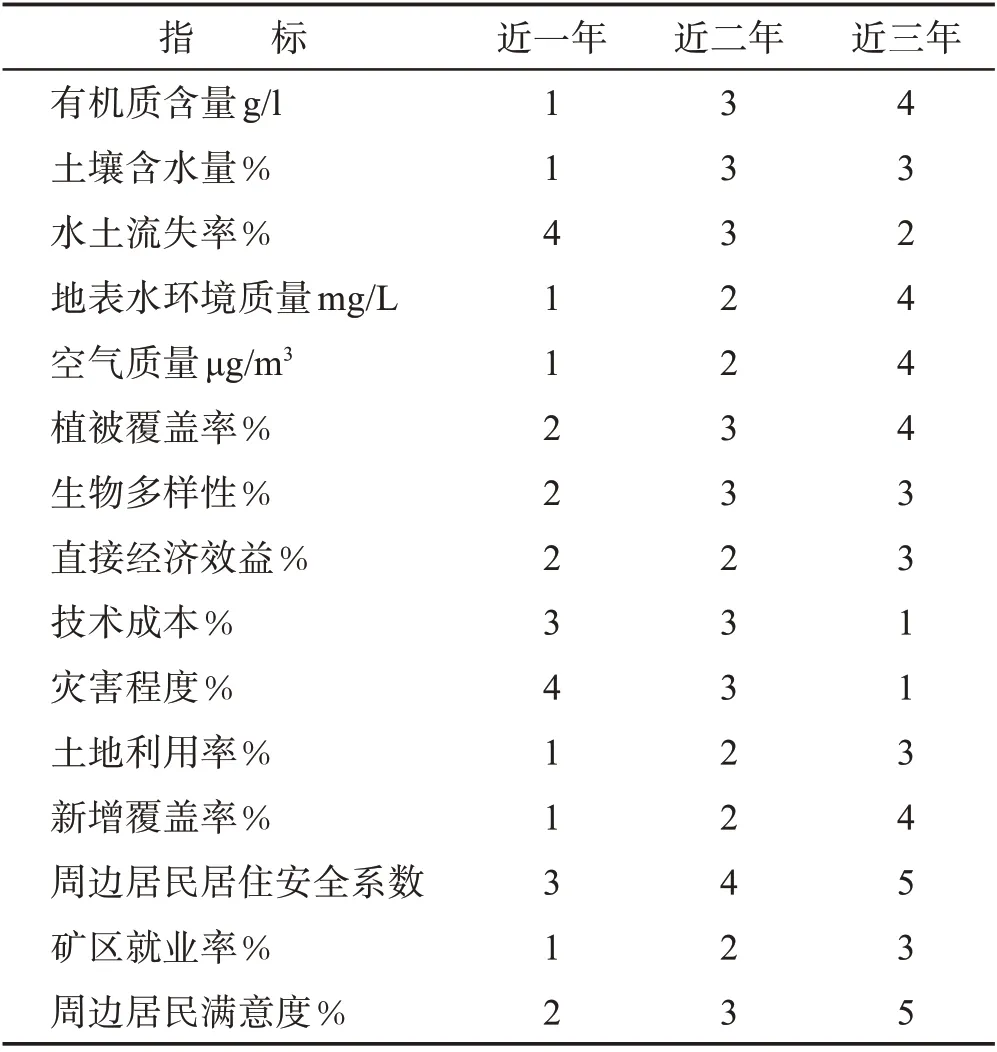
表3 专家评分结果Table 3.Expert scoring results

采用本文构建的基于DEA算法的矿山修复生态效益评估模型对该矿区生态效益进行评估，将专家评分结果与本文模型的评估结果进行对比，得出本文模型对矿区生态效益评估结果（表4）。

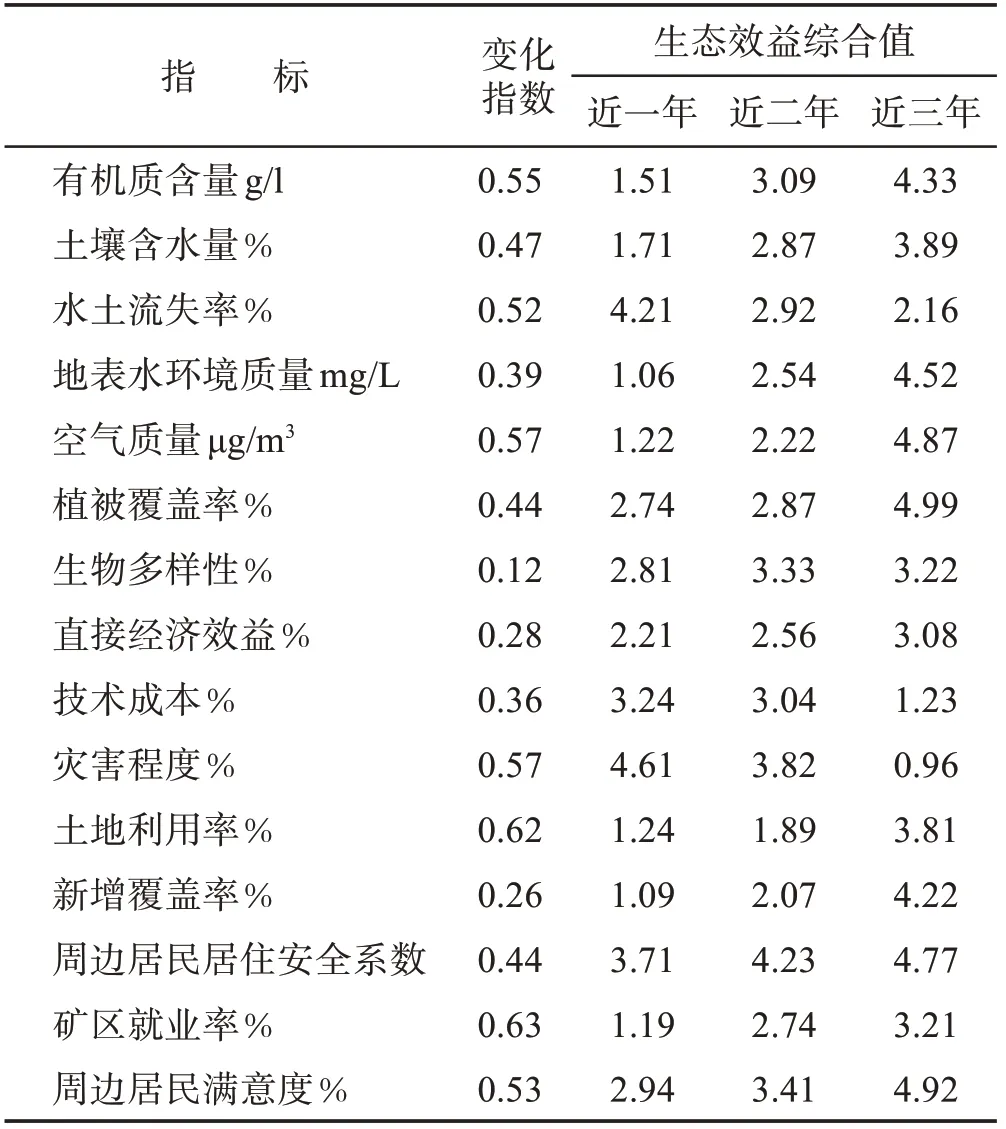
表4 本文模型评估结果Table 4.Evaluation results of this model

综合分析表3和表4可知，使用本文模型对该矿区修复生态效益指标评估结果与专家评分结果较为接近，且该评估结果更为精确，该矿区生态效益综合值一目了然，而且能有效评估该矿区各个指标的变化指数，由此可见本文模型具有较高的有效性。

2.2 评估准确性分析

以均方根误差作为衡量指标，进一步验证本文模型的评估准确性。取10个三级评估指标，计算其均方根误差，对比本文构建的基于DEA算法的矿山修复生态效益评估模型、文献[5]模型和文献[6]模型的评估平均均方根误差如表5所示。

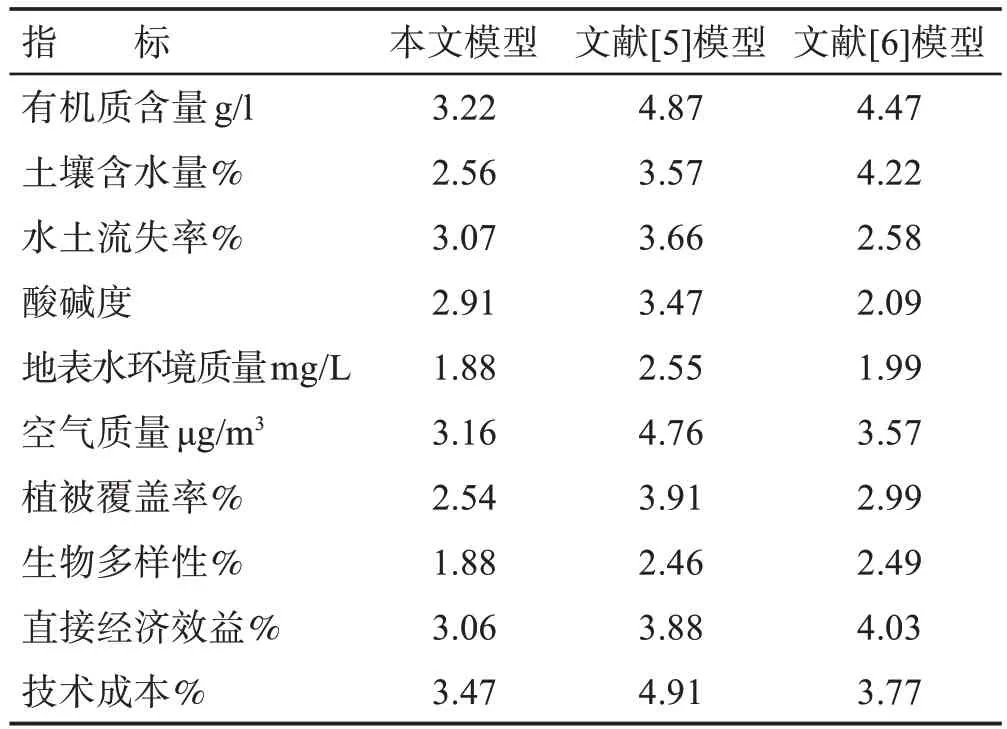
表5 三种模型评估均方根误差Table 5.Root mean square errors of evaluation by three models

分析表5可知，本文模型的评估均方根误差结果相较文献[5]模型和文献[6]模型评估的均方根误差结果而言，相对较低，且其平均均方根误差为2.78，而文献[5]模型和文献[6]模型的平均均方根误差分别为3.80和3.22，该结果表明，本文模型均方根误差最低，其修复生态效益评估结果与实际结果接近度最高，该模型具有较高的评估准确性。

2.3 评估效率分析

测试不同数据量情况下三种模型的评估效率，结果如表6所示。

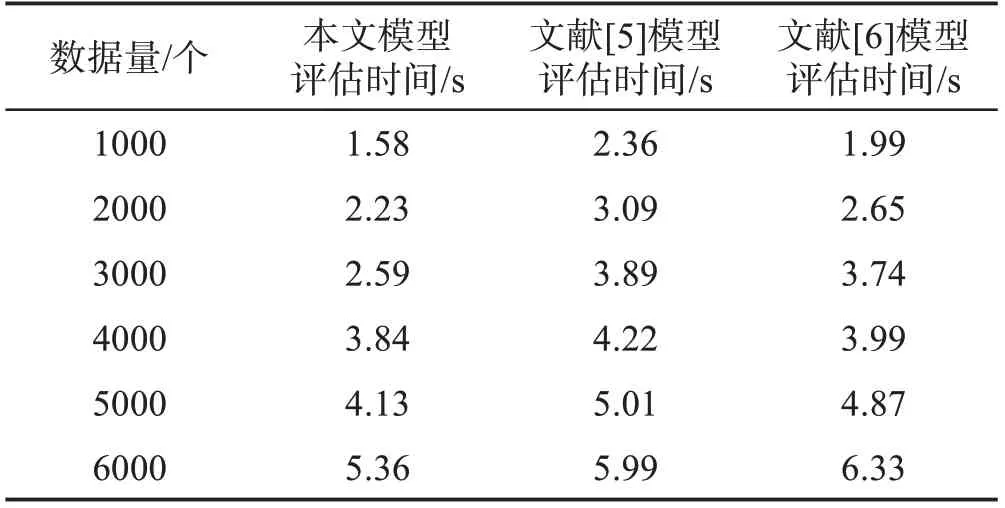
表6 三种模型评估效率结果Table 6.Results of evaluation efficiency of three models

数据量/个 本文模型评估时间/s文献[5]模型评估时间/s文献[6]模型评估时间/s 7000 8000 9000平均耗时/s 6.02 7.21 8.87 4.64 6.49 8.06 9.54 5.41 6.87 8.44 10.22 5.46

分析表6可知，随着数据量增加，三种模型评估耗时也随之增加，其中本文模型的评估时间最短，平均耗时最低，且与文献[5]模型和文献[6]模型平均耗时相差0.82s左右，差值较大，表明本文模型评估效率较高。

2.4 模型稳定性分析

以灵敏度为实验指标，绘制三种评估模型的ROC曲线，验证三种模型稳定性能，三种评估模型ROC曲线如图1所示。

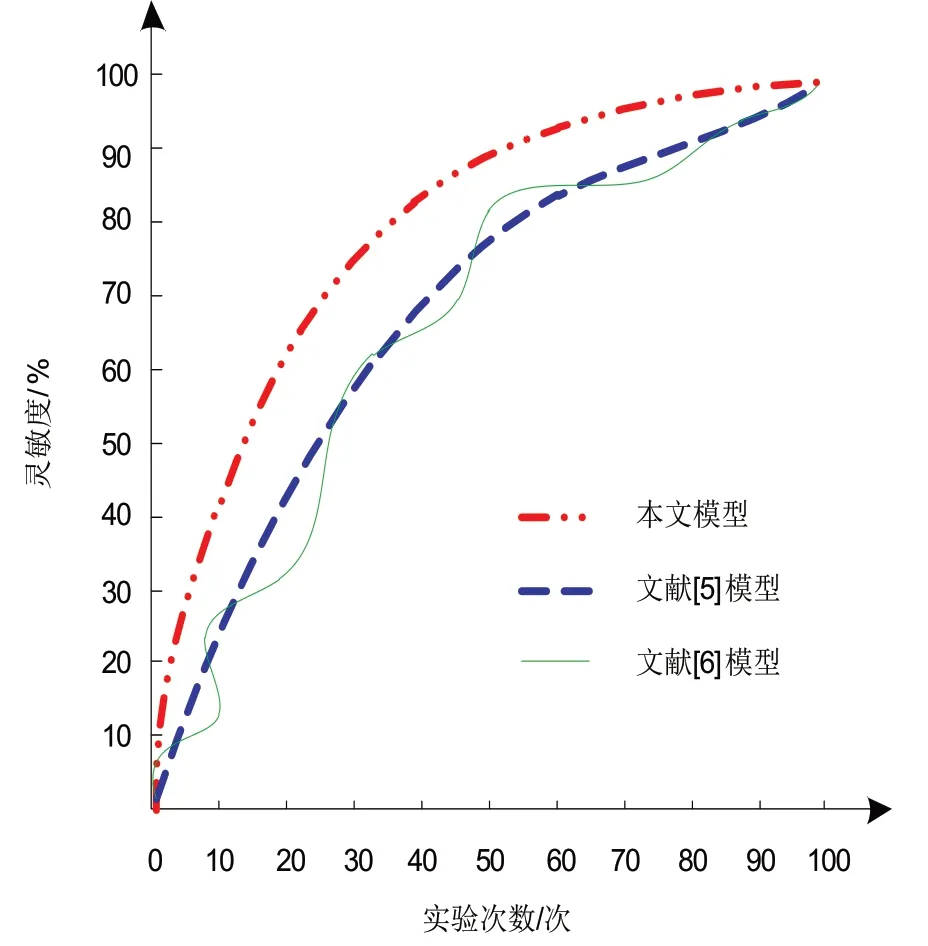
图1 三种评估模型ROC曲线Figure 1.ROC curves of three evaluation models

分析图1可知，在三种评估模型的ROC曲线中，文献[6]模型ROC曲线波动较大，而文献[5]模型与本文模型ROC曲线较为平滑，表明本文评估模型和文献[5]模型稳定性能较好，且本文评估模型的灵敏度数值均高于文献[5]模型和文献[6]模型，由此可知，本文模型稳定性能优越。

3 结语

针对传统的矿山修复生态效益评估模型存在评估准确性低、评估时间长的问题，本文利用DEA算法建立矿山修复生态效益评估模型。

（1）将该模型应用在矿山修复生态效益评估中，根据矿山地理区域特征和其修复生态效益目的，构建具有客观性、独立性、系统性等特点的矿山修复生态效益指标体系，利用本文评估模型评估矿山修复生态效益指标，为矿山可持续发展提供相应科学依据。

（2）实验结果表明：本文模型对矿区的修复生态效益指标评估结果与专家评分相差较小，且评估数值更为精确；均方根误差值较对比模型低，且平均均方根误差值仅为2.78，评估准确性较高；随着数据量增加，模型评估耗时也增加，评估平均耗时仅为4.64s，模型评估效率高；模型ROC曲线较为平滑，且灵敏度数值均较高，模型稳定性能强。

（3）虽然本文模型在评估矿山修复生态效益时展现了极高优越性，但该模型依然存在一定局限性。首先DEA算法虽然对每个决策单元展开横向比较，但无法为研究人员提供理论上的最大数值，其原因在于DEA算法是非参数算法，统计假设检验具有一定难度。其次矿区环境复杂，对其进行修复生态效益评估时间跨度较长，且评估过程存在多个环境、多个层次，复杂性较高，各个指标之间关联度较高时，会发生评估多重共线性情况。因此，对矿山修复生态效益评估需各个部门及各类人才共同协作，以提升评估最终结果。