基于智能预测和机理模型的换热网络清洗决策
蒋宁,张元毅,范伟,赵世超,徐新杰,徐英杰
(浙江工业大学机械工程学院,浙江 杭州 310023)
随着工业大数据和工业物联网的发展,对过程工业建立智能化监控平台可以进一步提高生产安全和生产效率。现役的石化装置中布置了较多的传感器,但仅实现关键指标的阈值报警,而不能实现对生产运行性能的预测及优化。换热网络是过程工业系统中重要的能量回收单元,提高换热网络的运行性能可以有效减少公用工程能耗。目前,针对换热网络的研究,主要是通过换热网络的优化设计和优化改造方法,提高换热网络的能量回收能力。对于石化装置的换热网络而言,换热器长时间处在高温高盐的运行条件,导致换热器性能衰退,进一步影响换热网络的运行性能。
目前提出的换热器结垢模型,主要是以Kern提出的污垢增长的微分方程为基础,综合考虑其他不同因素对换热器结垢的沉积率和剥蚀率的影响。Ebert 和Panchal提出的阈值结垢模型认为化学反应可以加快污垢生长,剪切效应可以减缓污垢生长,当化学反应和剪切效应的作用处于平衡时,此时污垢生长缓慢;Knudsen 等和Polley 等对该模型进行了改进,获得了更好的预测精度。随着智能算法的发展,可以进一步挖掘数据隐藏的关系,更多地关注运行条件对换热器性能的影响。樊绍胜基于影响污垢变化的因素有部分关系已知的特点,提出一种基于灰色理论的污垢预测方法。徐志明等采用改进的灰色理论的污垢预测方法,综合考虑未来的一些扰动因素对污垢预测的影响,通过在建模过程中及时去掉数据集中的旧数据补充新数据,实现换热器性能的中长期预测。Sun 等采用遗传算法优化后的支持向量机模型,优化后的训练精度要明显优于标准的支持向量机模型。神经网络算法(ANN)具有较强的学习能力和构建非线性的复杂关系的优点,被广泛用于工业数据的建模。Aminian 和Shahhosseini采用前馈网络和反向传播算法相结合的方法对神经网络模型进行训练,通过试错法找出隐藏层数和神经元数的最佳组合,与实验数据相比,ANN模型的平均相对误差为26.23%,ANN 模型对原油污垢热阻变化率的预测精度明显优于阈值结垢模型。Sundar等提出以深度学习为基础的预测模型,对错流式换热器中的污垢形成进行预测分析。基于该深度学习模型的结果表明,污垢热阻绝对平均预测误差低于10kW,系数超过99%。
换热器结垢是一个长期存在的问题,而由结垢所造成的换热器换热效果衰退,一方面需要通过更严格的操作条件来减缓换热器结垢,同时需要增加冷热物流末端的公用工程供应以满足工艺生产要求。通过对结垢的换热器制定定期清洗方案,可以重新恢复换热器的传热性能。Smaїli 等提出,污垢可被大致分为两层,即新鲜层和老化层,老化的程度决定了沉积物的状态,也决定了污垢层去除的难易程度。针对这两层,操作员可以选择不同的清洁方式,清洗方式可分为溶剂清洗和机械清洗。溶剂清洗无法彻底清除沉积物,而在污垢沉积物老化超过一定程度之前,机械清洗是不经济的。基于两层沉积模型优化换热器清洗周期,Ishiyama 等提出沉积模型和经济模型,也提出了超清洗周期的概念,即一个清洗周期包括数个子循环,每个子循环的长度由给出的经济模型进行评估。Pogiatzis等使用两种方法来生成混合清洁调度问题的解,第一个基于启发式行进算法,选定下一个子周期的清洁方法,最终选择机械清洗;第二种以每一个子周期长度为变量,选定溶剂清洗的数量,模拟3种情况,即基本情况、沉积速率变化、老化速率变化,找到每种情况最佳溶剂清洗次数和一个清洗周期的天数。但上述方法仅仅局限于对单台换热器清洗方案的研究,无法从系统集成的角度分析换热网络整体性能的变化,来制定清洗方案。
目前对换热网络的清洗决策主要是建立相应的混合整数非线性规划(MINLP)模型,通过不同算法进行求解以获得经济性的清洗方案。Pogiatzis等提出了一个MINLP模型,研究了热交换器的清洗调度问题;基于此,Georgiadis 等建立新的混合整数线性规划(MILP)模型,该模型没有考虑有关传热或结垢模型的非线性模型,对小型换热网络清洗问题,该模型能够实现全局最优性。樊婕等提出以换热器清洗的最大允许污垢热阻为优化变量,取代表示换热器是否清洗的二进制变量,将混合整数非线性规划问题(MINLP)转化成非线性规划问题(NLP),降低求解难度。这种求解模型对石化现场换热网络的性能监测比较少,同时为了获得最佳的经济性方案,而忽略了石化现场清洗换热网络其他因素的影响。Biyanto等采用帝国竞争算法(ICA)求解,通过该方法求解得到的清洗计划相比原来节省了约44.83%的传热损失,在44个月内节省了105 万美元,占结垢损失费用的22.12%,具有较好的经济性。Xiao等提出了一种遗传/模拟退火算法(GA/SA)同时优化柔性换热网络和清洗计划的新方法。与以往的MINLP 模型不同,通过初次综合策略可以有效地消除同时多周期MINLP 模型中的大量的二元变量,进一步优化了换热网络中换热器的匹配关系及换热器传热面积和运行周期。Diaby 等采用遗传算法来求解在结垢和不同老化情况下,原油炼厂预热机组最佳清洗时间表的问题。与未优化清洗和不进行清洗时的原油炼厂预热机组相比,通过遗传算法优化得到的最佳清洗计划,可以实现较大的经济效益。
与单台换热器性能预测模型不同的是,换热网络由多台换热器组成,不同换热器性能变化对换热网络整体性能变化的影响不同,换热网络整体性能变化要比单台换热器性能变化更显著。目前对换热网络的清洗决策主要是建立相应的MINLP 模型,通过不同算法进行求解以获得经济性的清洗方案。这种求解模型对石化现场换热网络的性能监测比较少,同时为了获得最佳的经济性方案,忽略了石化现场清洗换热网络时一些其他因素,包括不同清洗准则的制定、公用工程成本的定价、停用清洗时间和换热器清洗成本的定价等的影响,这主要影响了最佳清洗的选择及经济性结果,而且也没有考虑清洗时无备用换热器的影响,在换热器停用清洗期间换热网络需要更多的公用工程来满足生产工艺要求,需要考虑停用清洗所带来的损失费用和清洗成本。因此,本文提出了一种基于智能预测和机理模型的换热网络清洗决策方法,通过将换热器智能预测模型与换热网络性能模拟模型相结合,获得换热网络的性能变化趋势,从而从网络整体性能变化角度来制定清洗方案,实现换热网络的高效运行。与原有的方法相比,该方法基于现役运行数据建立换热器性能智能预测模型,同时对换热网络整体性能进行监测,更能反映现役换热网络的性能状态。
1 基于数据的换热器性能智能预测
原油装置的换热器长时间处在高盐高温的运行状态,导致换热器结垢、性能衰退严重,传统的时间序列预测模型和污垢阈值模型对换热器性能预测差异较大,因此本文基于神经网络算法建立换热器性能智能预测模型,以获得换热器的性能变化趋势。
1.1 原油换热器阈值结垢模型
传统污垢热阻的计算公式中参数较多,测量不方便,同时计算误差较大,对于给定的流体组成和换热表面状况,换热设备换热面的温度和流速是影响设备中原油污垢生长的重要因素。因此,针对流速和温度两个重要因素,学者提出了有关温度和流速的原油换热设备结垢的经验公式,主要包括以下4种阈值模型。
Saleh 等提出的模型只考虑了温度的影响,未考虑流速对污垢形成速率的影响,该模型主要运用在过渡区域,见式(1)。
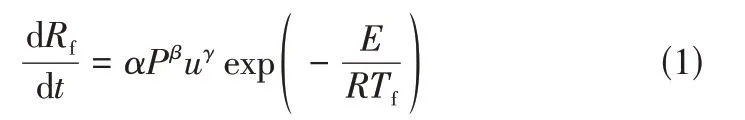
1995 年,Ebert 和Panchal提 出 了 原 油 污 垢 生长的阈值模型,该模型表明污垢的生长不仅取决于化学反应和温度,还与管壁的剪切应力有关,见式(2)。
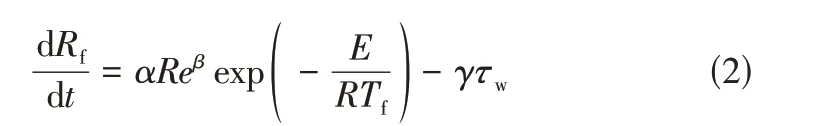
2002 年,Polley 等对原油结垢的阈值模型进行了改进,模型中引入了普朗特数,见式(3)。
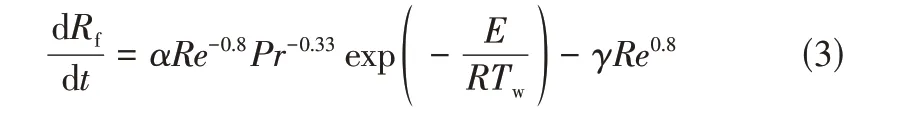
2006 年,Jafari 和Mejidi提 出 了 一 种 新 的 模型,见式(4)。
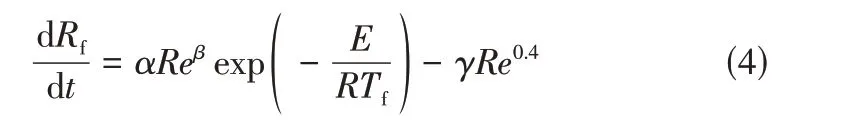
表1 的实验数据是某原油换热器在60h 内的11 组实验数据,包括时间、流速、雷诺数、温度和污垢热阻变化率。

表1 各维度数据分布指标表
该实验的污垢热阻变化曲线如图1所示。通过拟合上述阈值模型的经验公式,发现无法通过以往的经验公式较好地拟合该台换热器的阈值结垢曲线。因此,根据阈值结垢模型的一般方程表达式,拟合得到式(5),拟合公式的为0.07886,为0.0018,绝对平均误差为0.0005m·K/(kW·h),相对误差率为77%。从表1中可见,该台换热器的流速变化区间小,导致不同时刻雷诺数()基本相同,以致传统阈值模型中的关键参数成为一个固定参数,使得针对该实验的阈值结垢模型不能反映流速的影响,导致经验公式在该实验数据上的失效。根据以往的研究可知,阈值结垢模型反映的是温度和流速之间的制约和平衡关系,往往实验中需要较大范围的温度和流速的实验,以探究不同温度和不同流速之间的关系;而对于较小范围的温度和流速的实验,由于温度范围或流速范围较小,无法发现两者之间的内涵关系,传统理论研究的经验模型无法适用。
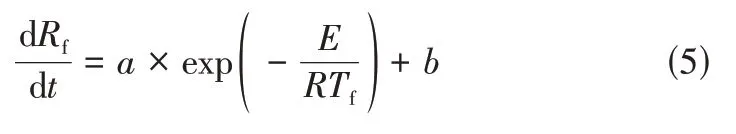
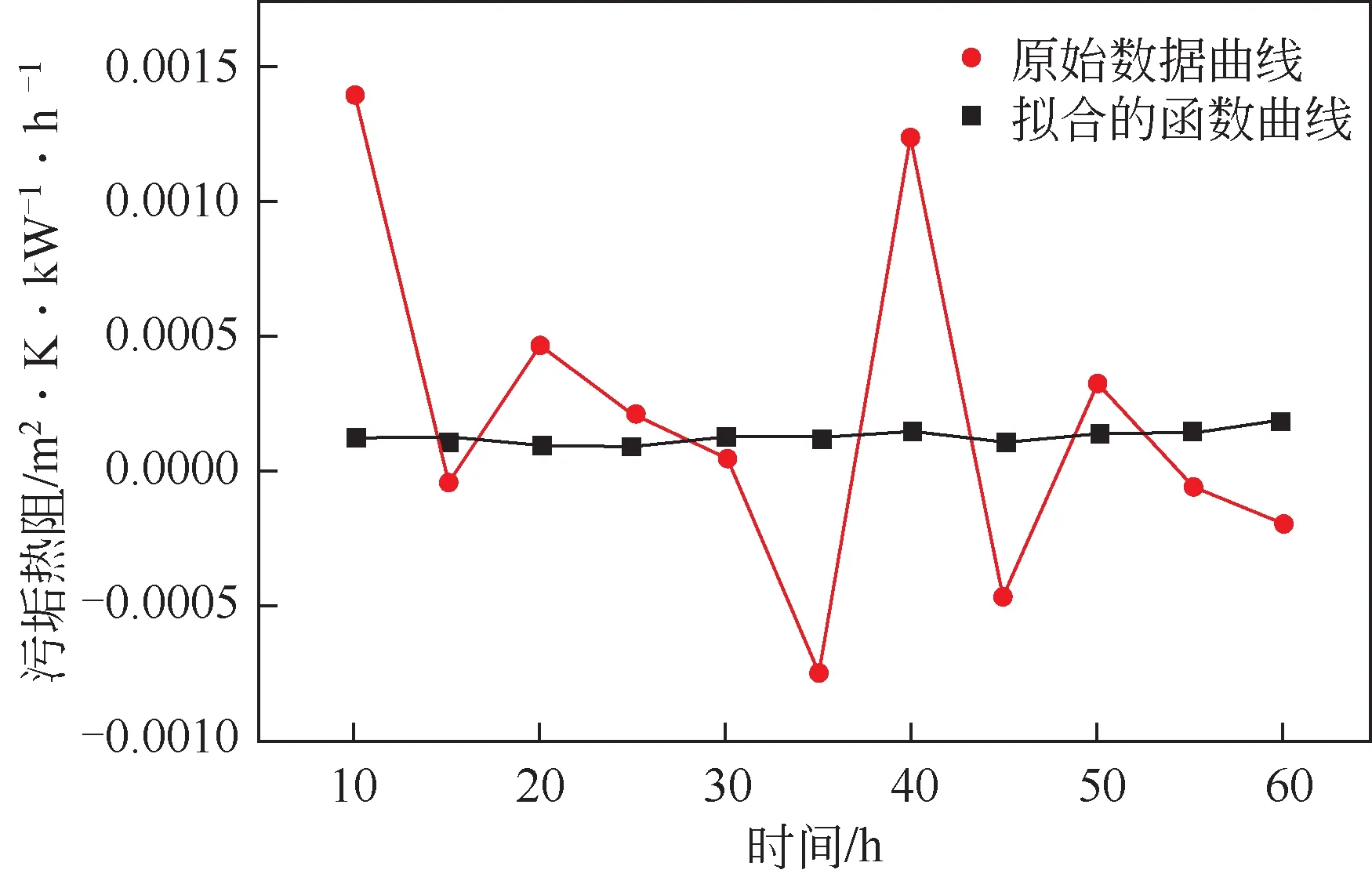
图1 经验模型的拟合结果
1.2 神经网络预测模型建立
随着工业数据规模的扩大,支持向量回归(SVR)、自适应增强算法(Adaboost)等传统的机器学习对大数据模型很难有较好的训练效果,而神经网络等深度学习算法的发展,具有广泛的适用性,可以充分挖掘数据的内在关系,可以对换热器运行数据建立更好的智能预测模型,神经网络模型的建立步骤如下。
(1)收集换热器结垢数据,该数据集由时间、黏度、压力、流速、氧气含量、热负荷、管壁温度、管腔温度和污垢热阻9个维度数据组成。
(2)根据归一化公式,对该数据集各维度数据采用线性函数归一化处理,采用归一化处理的数据集,各维度数据都分布在[0,1]的范围内。
(3)选择神经网络神经网络层数,输入层为时间、黏度、压力、流速、氧气含量、热负荷、管壁温度、管腔温度8 个结点,输出层节点数为1 个(污垢热阻)。选择恰当的隐藏层层数,神经元数和激活函数。
(4)采用不同的优化器训练BP 模型,直到模型达到理想的预测性能,从而建立BP 神经网络预测模型。采用不同的回归模型评估指标平均方差(MSE)、均方根误差(RMSE)和差等反映回归模型的预测结果的优劣。
本文通过对文献[25]中的原油换热器的污垢数据采用神经网络预测模型,经参数训练后,得到最佳的参数组合为神经元数为100,隐藏层数为1层,激活函数为linear,优化器为adam方法,训练样本为600组,与SVR模型和Adaboost模型训练的结果曲线如图2所示。从图2中可以看出,采用神经网络(BP)模型和SVR 模型的预测结果明显优于Adaboost 模型。BP 模型和SVR 模型在训练集和测试集上都逼近原始数据曲线,训练效果较好,而Adaboost模型在训练集和测试集均无法逼近原始数据曲线,导致训练效果较差。不同算法的污垢预测模型的评价指标结果如图3所示。从图3中可以看出,采用BP 模型和SVR 模型在MAE、RMSE 和三个指标上相近,采用Adaboost 模型在MAE、RMSE和三个指标上要明显劣于神经网络模型和SVR模型,神经网络模型在此三个指标上反映出的结果最优。因此,小数据集上,BP 模型和SVR 模型都具有较好的预测效果,Adaboost模型预测结果较差。随着工业数据规模的增加,神经网络算法可提供更好的优化器算法,能够快速地训练得到最佳的参数组合。传统的机器学习方法如SVR 算法,当数据量较大时,需要求解的高阶矩阵存储和计算将耗费大量的机器内存和运行时间,导致复杂度增加,不适合大规模数据的建模。随着不同类型算法的提出,为不同结垢机理的换热器运行数据建立智能预测模型提供了更多选择。
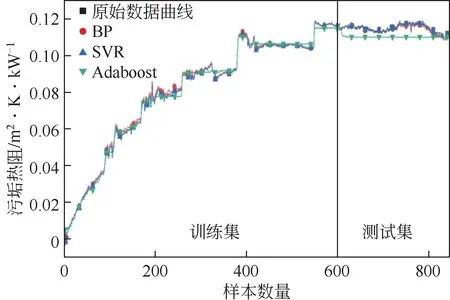
图2 与传统机器学习模型结果比较
图3 不同预测模型评价指标结果对比
2 换热网络的性能模拟模型
本节建立基于数据和机理的换热网络性能预测方法,实现对现役换热网络的性能预测。
换热网络是由数量较多的换热器,通过换热器之间的串联和并联,实现冷热流体的热量交换。因此,换热网络性能的模拟可以先模拟单个换热器的性能,再根据换热网络中换热器之间上下游和串并联关系求解获得。
在以往的研究中对单个换热器性能的模拟,通常假设换热器没有发生相变,基于能量守恒定律和换热器传热方程,此时换热器性能模拟的具体计算见式(6)~式(8)。
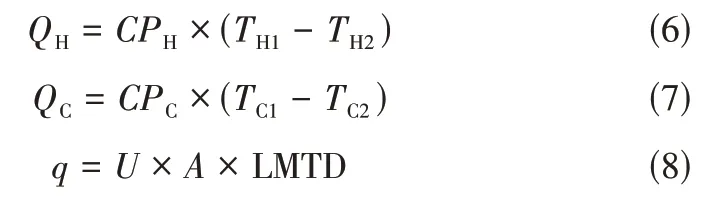
其中,LMTD 为对数平均温差,计算公式见式(9)。
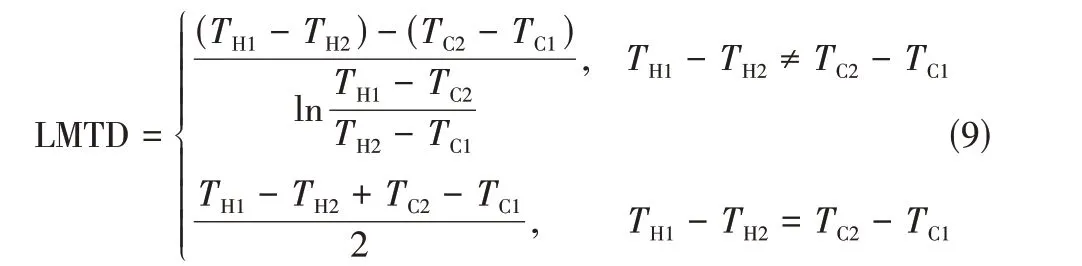
为简化计算,设参数,表达式见式(10)。
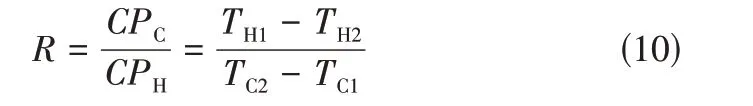
当≠1时,有式(11)。
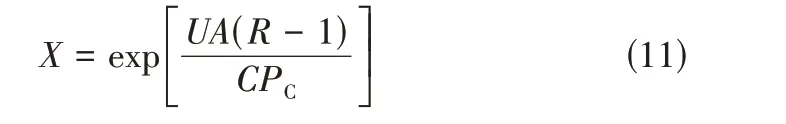
依据对以及的定义,可将公式转换为式(12)、式(13)。
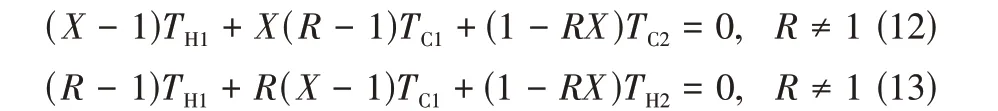
当=1时,公式可以转换为式(14)~式(16)。
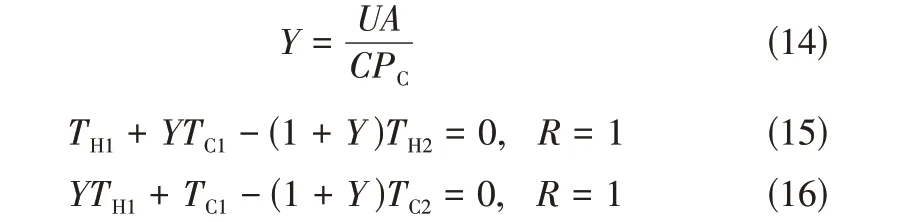
由此可见,在已知换热器的换热面积、冷热物流通过此换热器的进口温度以及热容流率、传热系数的信息后,可求得该换热器的或以及值,由此构成换热网络性能模拟非线性方程组的、、系数矩阵,则式(12)、式(13)或式(15)、式(16)这两个方程仅有两个未知量(热物流的出口温度和冷物流的出口温度),对于一个由台换热器组成的换热网络而言,则共有2个方程,通过求解这些方程,可以得到换热网络的温度分布。最后根据温度分布与物流目标温度,可求得换热网络公用工程的消耗量。
3 换热网络性能预测方法
3.1 方法介绍
随着工业物联网的发展,石化公司对现有的石化装置布置了多种传感器。虽然石化现场能够采集到换热器的温度、流速、压力等工况运行数据,但是对采集数据的应用仅停留在简单的计算和阈值报警,因此失去了让数据促进生产节能增效的作用。通过对采集的换热器运行数据建立神经网络预测模型,可以进一步改进对换热器运行性能的监测,实现石化生产的智能化。
由于换热网络中换热器之间存在上下游和串并联的关系,导致换热网络中换热器之间相互耦合,从而导致不同换热器的性能衰退对下游换热器性能和换热网络整体性能的影响不同。单纯通过换热网络的进出口温度数据建立神经网络性能预测模型来实现对网络性能预测,模型的预测精度有限,同时不能反映换热网络中不同换热器的性能衰退对网络性能的影响,因此将单台换热器智能预测模型与换热网络性能模拟模型相结合,实现对换热网络性能的预测。
目前石化现场采用的清洗方案,主要是根据换热器热性能衰退到一定程度时,对该台换热器进行停用清洗,该清洗方案对换热器的干预较少,换热器性能可能长时期处在较差的运行状态,从而导致换热网络需要较多额外的公用工程能耗供给以满足生产工艺要求。因此本文提出基于换热网络整体性能来制定清洗方案的方法,当多台换热器同时发生性能衰退时,换热网络的整体性能变化要比单台换热器性能变化更显著,因此从换热网络整体性能变化的角度制定清洗方案,可以提前对换热器运行性能进行清洗干预,使得换热网络整体性能保持在较好的状态。
3.2 求解流程
基于智能预测和机理的换热网络性能预测方法的求解流程如图4所示,具体实现步骤如下。
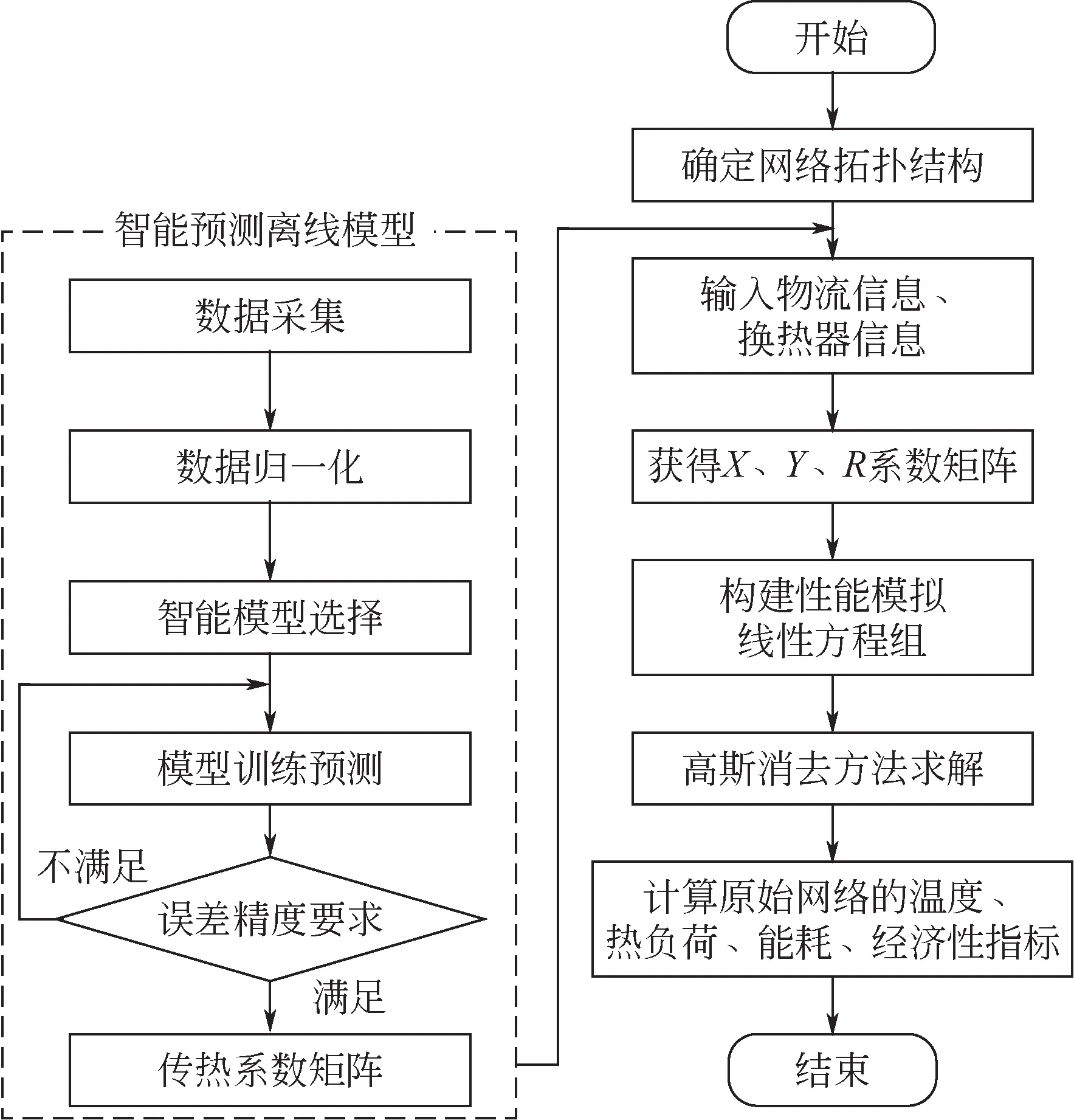
图4 本文方法的流程图
(1)确定网络拓扑结构
根据现役的换热网络结构图,确定换热网络中换热器的拓扑结构关系,将网络结构信息编写为可识别的矩阵信息。
(2)输入传热系数矩阵
通过换热器运行工况数据的采集、数据归一化处理、预测算法的选择和训练预测,获得换热器运行周期内预测的传热系数值,建立换热器智能预测模型,以满足模型预测误差精度要求。将不同换热器的传热系数数据构建换热网络的传热系数矩阵,传递给换热网络性能模拟模型。
(3)换热网络物流信息和换热器信息
收集换热网络的物流信息,包括冷热物流的进出口温度、热容流率、质量流量等;收集网络中换热器的信息,包括换热器的面积、传热系数等。
(4)获得、、系数矩阵
对步骤(1)和步骤(3)得到的换热器参数信息,获得换热网络性能模拟非线性方程组的、、系数矩阵。
(5)构建性能模拟线性方程组
对步骤(1)~步骤(4)得到的换热网络结构与参数信息,建立换热网络的性能模拟模型,给出该网络性能模拟的线性方程组。
(6)采用高斯消去法求解
对步骤(5)得到的线性方程组,采用高斯消去方法进行求解,获得所建立的线性方程组的解集。
(7)计算每天换热网络的性能指标
对步骤(6)求解得到线性方程组的解,根据步骤(1)换热网络拓扑结构信息,确定换热网络的温度分布,从而计算每天公用工程能耗和运行成本的变化情况。
本文在MATLAB2018b 环境下对上述方法进行了具体实现。在此基础上,进一步研究不同清洗方案对换热网络的影响,开展换热网络的清洗决策。
4 案例研究与分析
该案例为一个原油精馏单元的换热网络,该换热网络包括7条热物流和3条冷物流,物流数据如表2 所示,网络结构如图5 所示,图5 中红色线条代表热物流,蓝色线条代表冷物流,流股上的数字是流股的进出口温度,流股末端的斜体数字代表物流热容流率,位于中间换热的圈内数字代表中间换热器,位于流股末端的圈内字母代表公用换热器。该换热网络的换热器的总传热系数都为0.4kW/(m·℃),为换热器使用前总传热系数的初始值,换热网络公用工程总能耗为166000kW,年度公用工程费用6330000USD/a, 年操作时间8400h/a。
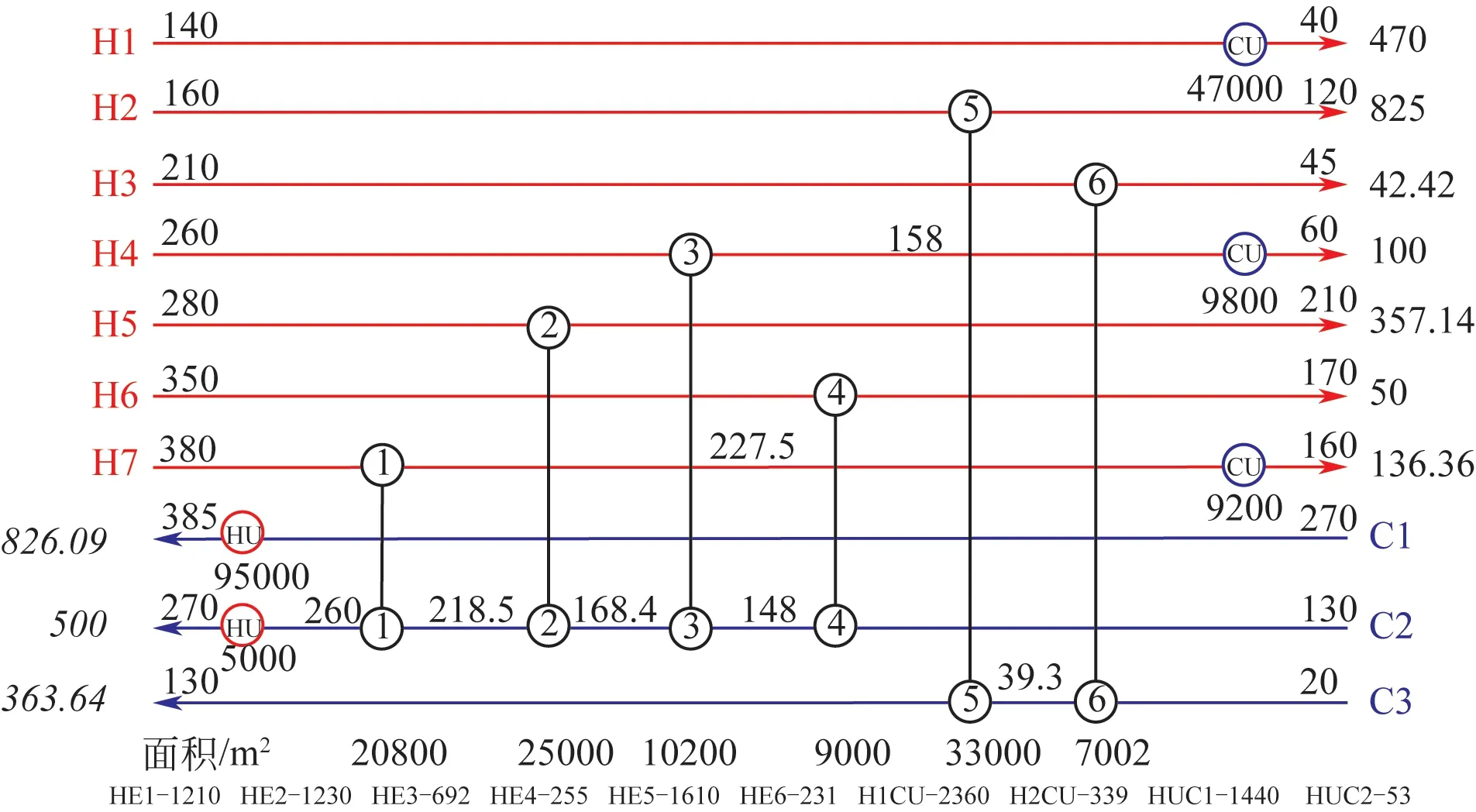
图5 现有换热网络结构图
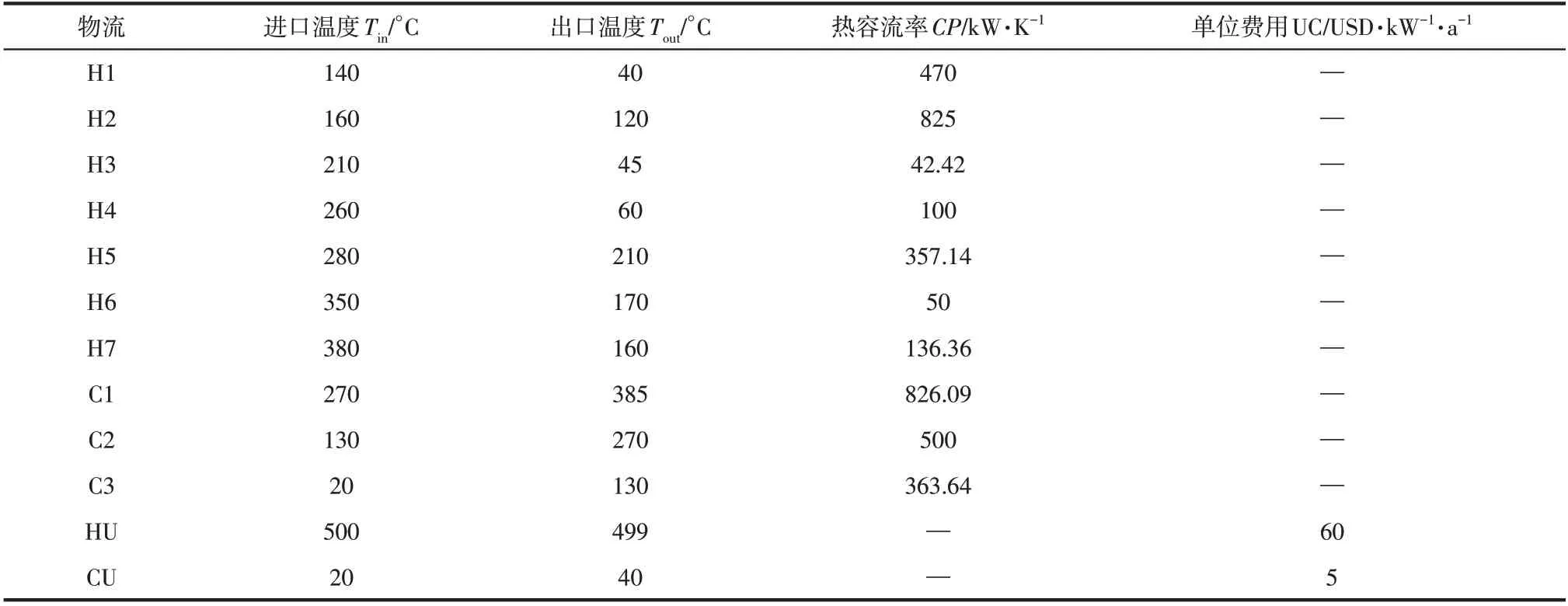
表2 物流数据表
4.1 换热网络性能预测
根据该换热网络的基本数据,灵敏度分析的计算结果如图6所示,该换热网络中HE5是最重要的设备,HE5性能衰退所导致的换热网络公用工程能耗增加最多;HE1 和HE2 是次重要设备,这两台换热器的性能衰退也会引起换热网络公用工程能耗的增加;HE6的性能衰退对换热网络的公用能耗增加影响较小,这主要是因为该台换热器换热面积较小,换热能力较弱,同时处于冷物流起始段第一个换热器,因此引起的冷物流终端温度变化较小,进而所增加的公用工程能耗较小。
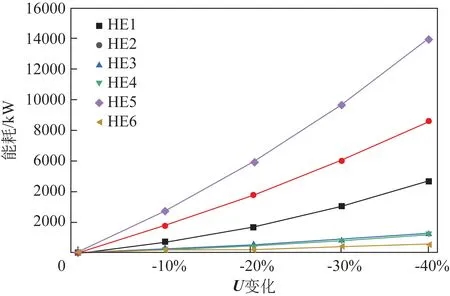
图6 换热网络关键设备灵敏度分析
为进一步反应换热网络的整体性能随换热器性能衰退的变化,考虑关键的HE1、HE2和HE5传热系数年度的变化情况,其中HE1 和HE2 的传热系数变化曲线如图7所示,HE5的传热系数变化曲线如图8 所示,经过60 天后,HE1 和HE2 的传热系数降为初值的74.63%,HE5 的传热系数降为初值的67.43%;HE1和HE2的传热系数在275天后趋于平缓,为初值的58.69%,HE5的传热系数在200天以后趋于平缓,为初值的58.84%。
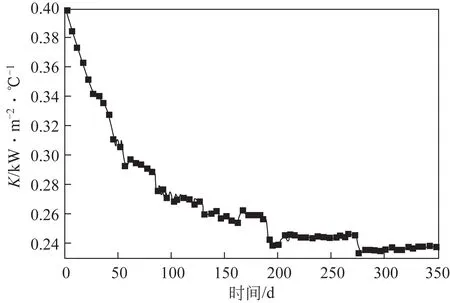
图7 HE1和HE2换热器传热系数时间变化曲线
图8 HE5换热器传热系数变化曲线
经过换热网络性能模拟模型计算得到的热交换网络公用能耗绝对增加量年度的变化曲线如图9所示。位于C2 物流上的HE1 和HE2,虽然HE1 和HE2具有相同的传热系数变化趋势,根据灵敏度分析可知,相同的性能衰退条件下,HE2所导致的热交换网络性能下降更严重,以致需要更多的公用工程能耗。位于C1 物流上的HE5,一方面其传热性能不断衰退,另外作为网络中最关键的设备,随着其性能的下降,导致在换热网络整个运行周期内,需要较多的公用工程能耗。若同时考虑HE1、HE2和HE5 性能发生衰退,因为HE1 和HE2 都位于冷物流C2 上,虽然两台换热器都以相同的性能衰退曲线,但是两台换热器的性能变化对整个网络的性能影响不同,HE2的性能衰退对网络整体的影响更大。研究发现,当两台换热器都发生性能衰退时,HE1 和HE2 两台换热器对热交换网络的性能影响并不是HE1 和HE2 两台换热器单独作用的之和,这主要是因为HE1 和HE2 换热器在热交换网络中存在着上下游耦合的关系。当HE1、HE2和HE5三台换热器同时发生性能衰退时,导致的热交换网络的性能衰退所需要的额外公用工程能耗是HE1 和HE2作用于C2物流和HE5作用C3物流两个部分分别引起的额外增加的公用工程能耗之和,这主要是因为HE5和HE1或HE2之间不存在耦合关系。
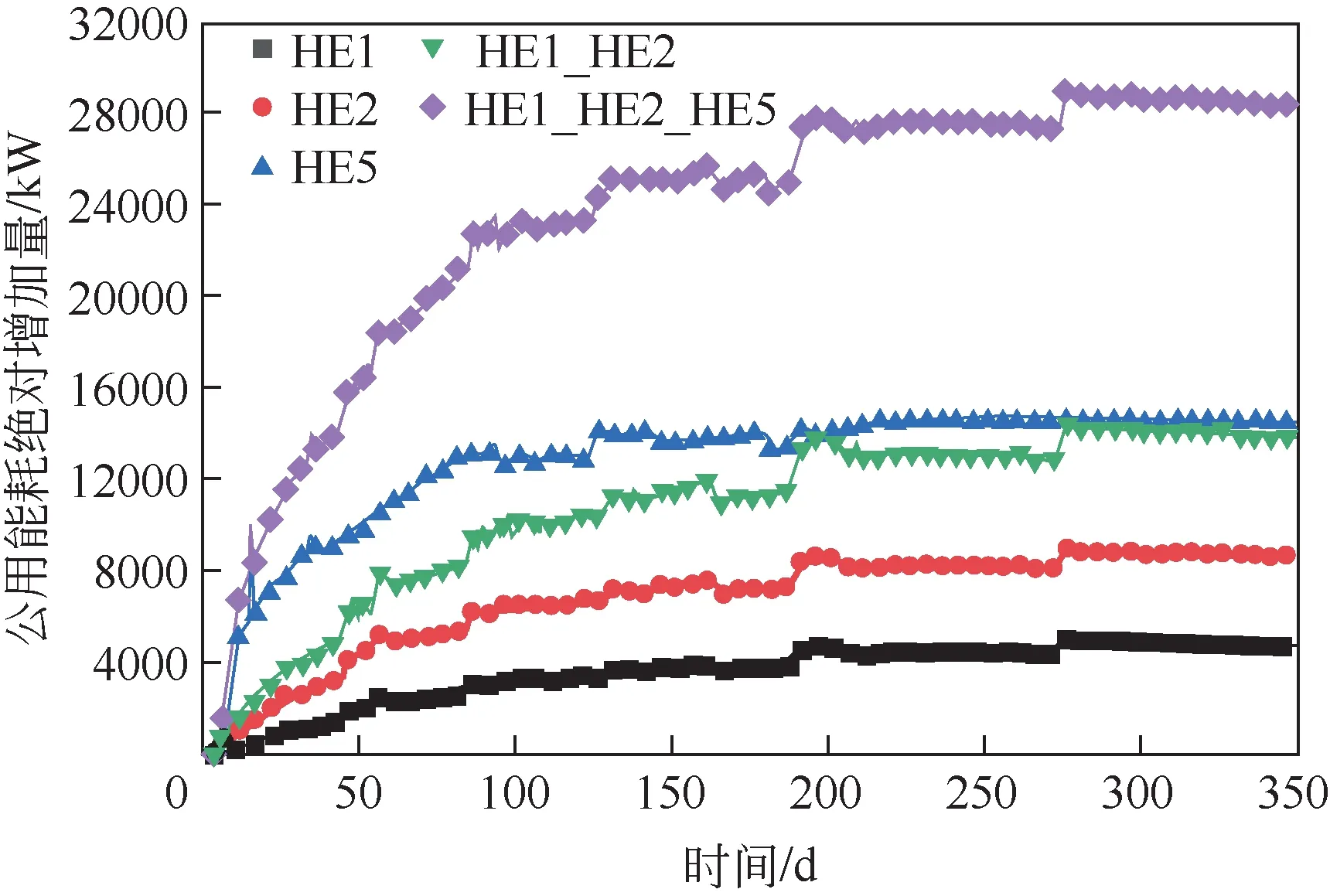
图9 公用能耗绝对增加量随时间的变化
根据图9的公用工程能耗绝对增加量随时间的变化曲线,通过计算可以得到日公用工程能耗绝对增加量随时间的变化,如图10 所示。热交换网络经运行一年后,当HE1 性能发生衰退时,日额外公用工程能耗最高为4.2×10kJ/d;当HE2性能发生衰退时,日额外公用工程能耗最高为7.5×10kJ/d;当HE5 性能发生衰退时,日额外公用工程能耗最高为1.3×10kJ/d;当HE1 和HE2 同时发生性能衰退时,日额外公用工程能耗最高为1.2×10kJ/d;当HE1、HE2和HE5都发生性能衰退时,日额外公用工程能耗最高为2.5×10kJ/d,由此可知当多台换热器同时发生性能衰退时,换热网络的整体性能变化要比单台换热器性能变化更显著。
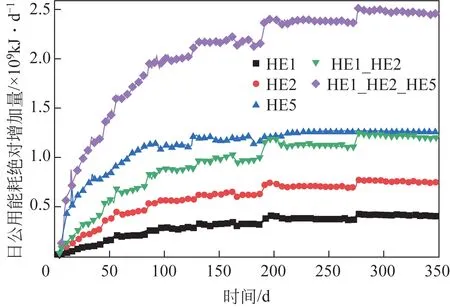
图10 日公用能耗绝对增加量随时间的变化
根据图10 日公用工程能耗绝对增加量随时间的变化,可计算得到年度总的额外公用工程能耗,如图11 所示。当HE1 性能发生衰退时,年度额外公用工程能耗增加量为1.09×10kJ/a;当HE2 性能发生衰退时,年度额外公用工程能耗2.07×10kJ/a;当HE5 性能发生衰退时,年度额外公用工程能耗3.87×10kJ/a;当HE1 和HE2 同时发生性能衰退时,年度额外公用工程能耗3.25×10kJ/a;当HE1、HE2 和HE5 都发生性能衰退时,年度额外公用工程能耗7.12×10kJ/a,其中年度额外热公用工程能耗和年度冷公用工程能耗为3.55×10kJ/a,年度热公用工程年费用增加704365USD,年度冷公用工程费用增加58697USD,年度公用工程能耗总费用增加763062USD,当HE1、HE2和HE5三台换热器都发生性能衰退时,年度额外需要公用工程能耗相对增加高达14.1%,年度额外公用工程能耗费用相对增加12.1%。
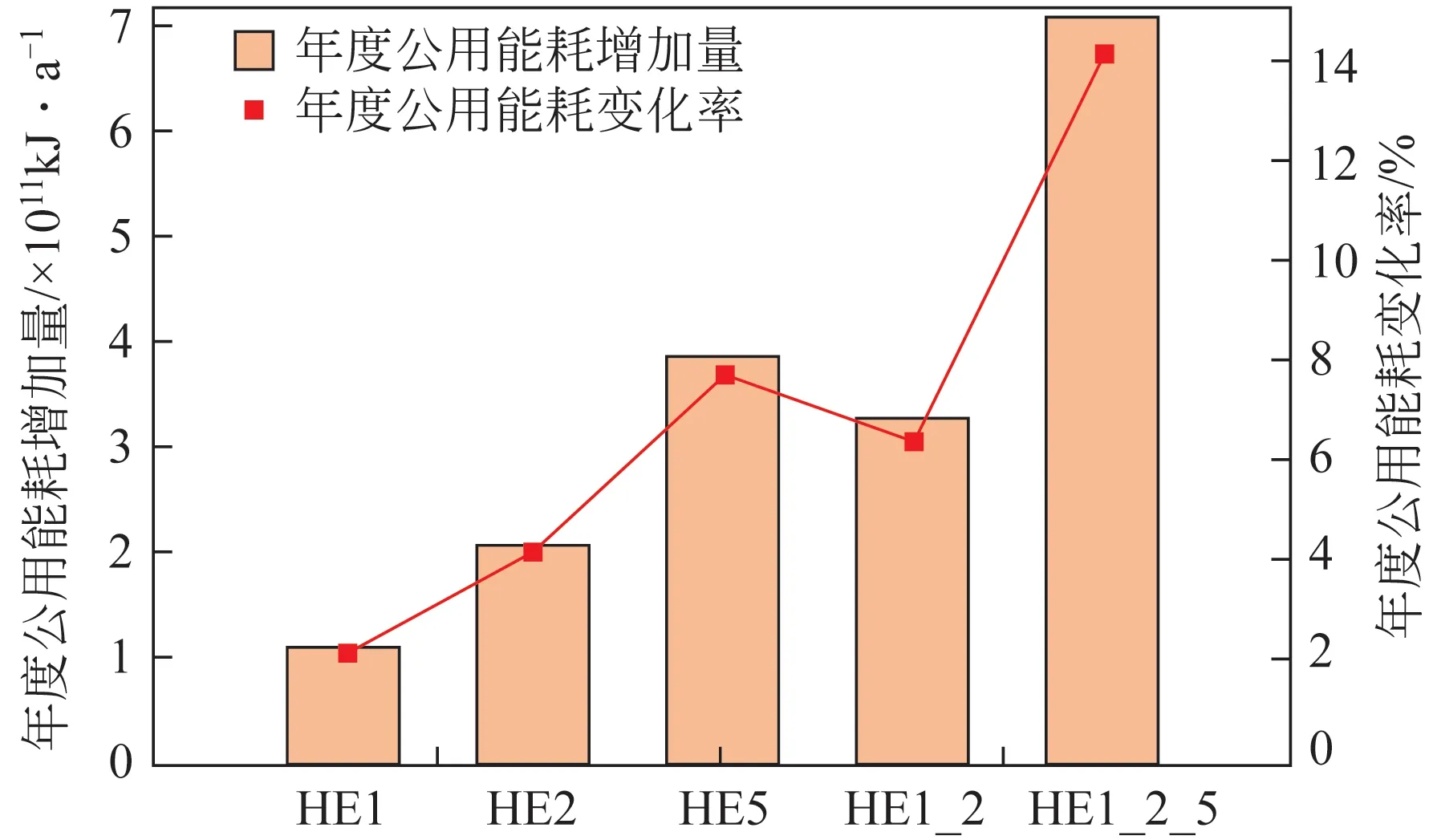
图11 年度公用能耗绝对增加量和年度公用能耗相对变化率
4.2 无备用换热器情况下的清洗计划比较
换热器的性能衰退一方面会影响换热器的运行安全,另一方面也会导致换热网络的换热效果下降严重,需要消耗更多的公用工程能耗满足工艺生产要求。因此需要通过制定合理的清洗方案使得换热器始终处于较高的换热性能状态运行,以减少公用能耗的增加。根据文献[27]得到,单台换热器每次清洗的成本为2.5USD,因此可得HE1、HE2和HE5的清洗成本分别为359.7USD/次、363.2USD/次、439.3USD/次。在实际的工业换热网络中,如果换热器存在备用换热器,则清洗时只需要切换到备用换热器,对生产的影响较小;如果换热器不存在备用换热器,则清洗时需要将换热器从网络中断开。当换热网络中的关键换热器没有备用换热器时,对性能衰退严重的换热器进行清洗时,需要将换热器从换热网络中断开,导致在该设备停用期间换热网络需要更多的公用工程来满足生产工艺要求,将这部分换热器停用期间的公用工程能耗费用作为清洗的损失费用。
(1)清洗方案1 当某台换热器性能衰退30%时,对换热器进行清洗。
如图12 所示,当HE1、HE2 和HE5 三台换热器性能都衰退30%时制定清洗方案1,由于三台换热器都没有备用换热器,此时清洗时需要将三台换热器停用一天进行清洗维修。此时HE1、HE2两台换热器的运行周期为85 天,HE1 和HE2 换热器每年各需要清洗4 次,HE5 换热器的运行周期47 天,HE5换热器每年需要清洗7次,即每年总共需要清洗15 台次。对图12 中日额外需要的公用工程能耗进行累加,清洗方案1的年度额外公用工程能耗为3.43×10kJ/a,其中年度额外热公用工程能耗为1.72×10kJ/a,年度额外冷公用工程能耗为1.72×10kJ/a,年度热公用工程费用增加340578USD/a,年度冷公用工程费用增加28381USD/a,年度公用工程费用增加368959USD/a。如图13所示,原始换热网络中,HE1回收热量20800kW,HE2回收热量25000kW,HE5回收热量33000kW,停用期间需要将需要停用清洗的换热器从网络中移出,因此需要通过流股末端的公用换热器提供额外的公用工程能耗来满足生产工艺要求,因此计算可得,HE1 和HE2 停用时的公用工程能耗为7.91×10kJ/d,HE5停用时的公用工程能耗为5.7×10kJ/d。HE1和HE2换热器每年需要停用4天,HE5换热器每年需要停用7天,则因停用所需要的额外公用工程费用作为清洗方案的损失费用,清洗方案1 的损失费用为76923USD/a。换热器清洗成本为5967USD/a,该清洗方案下年度总费用增加451849USD/a。与不清洗的原始网络额外增加的公用工程能耗和额外增加的公用工程费用相比,年度额外公用工程能耗下降51.7%,年度额外公用工程费用减少51.6%,年度额外总费用减少40.8%。
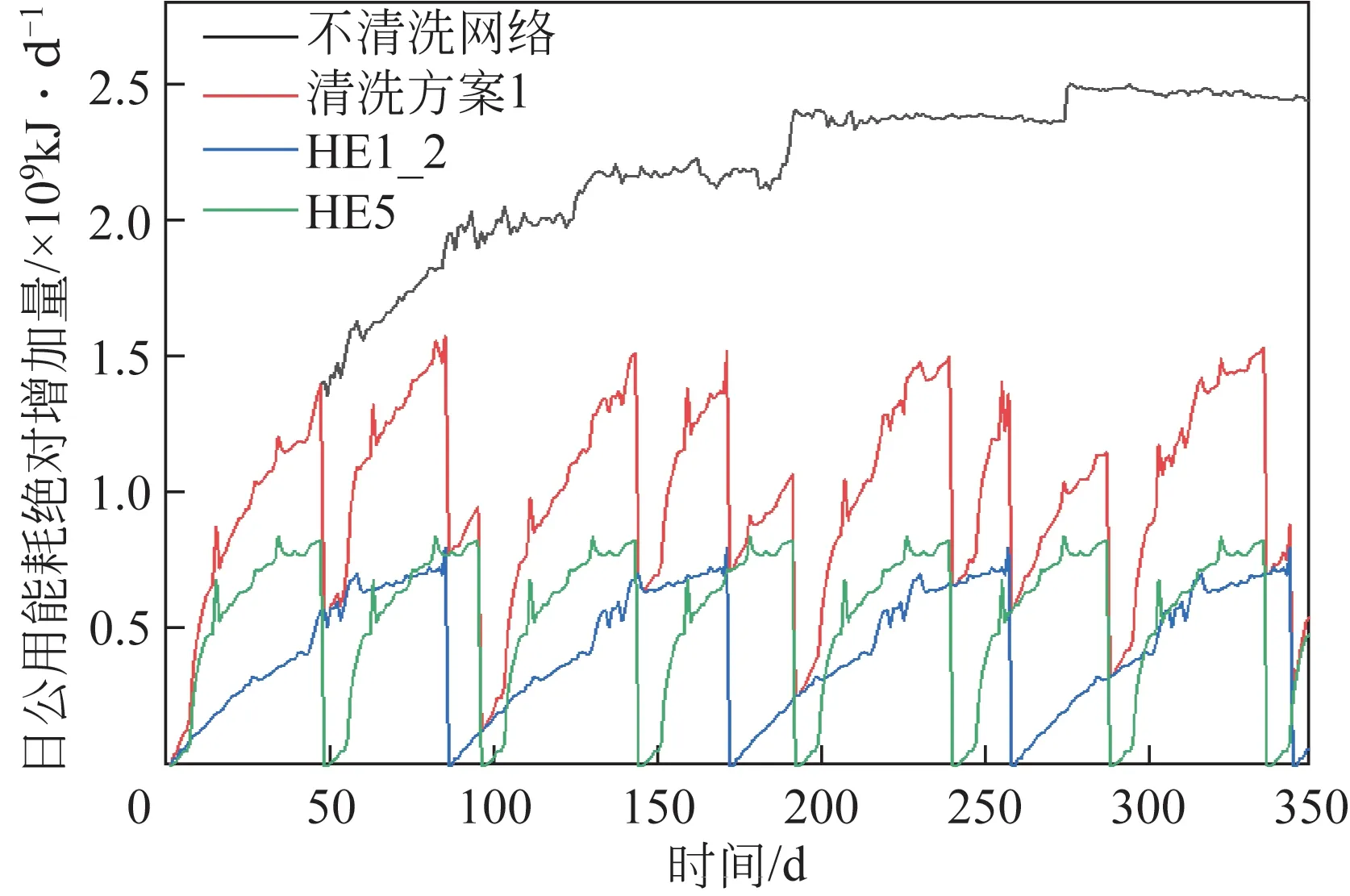
图12 当HE1、HE2和HE5性能衰退30%、停用24h的清洗方案
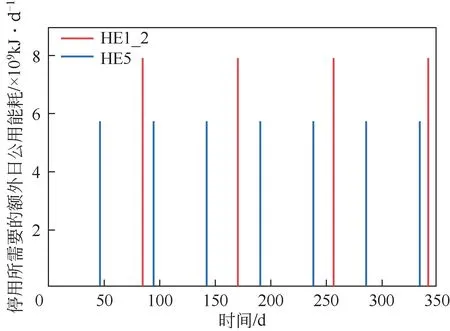
图13 HE1、HE2和HE5停用24h网络需要的额外公用工程能耗
(2) 清洗方案2 当换热器网络性能衰退10%,综合开展清洗决策。
如图14 所示,当HE1、HE2 和HE5 性能衰退导致换热网络公用能耗增加10%时,对HE1、HE2和HE5 三台换热器同时进行清洗,制定清洗方案2,换热器停用清洗时间为24h。按照该清洗方案2,此时HE1、HE2 和HE5 三台换热器的运行周期为50 天,HE1、HE2 和HE5 换热器每年各需要清洗6 次,即每年总共需要清洗18 台次。对图14 的日额外需要的公用工程能耗进行累加,清洗方案2的年度额外公用工程能耗为2.98×10kJ/a,其中年度额外热公用工程能耗为1.49×10kJ/a,年度额外冷公用工程能耗为1.49×10kJ/a,年度热公用工程费用增加295968USD/a,年度冷公用工程费用增加24664USD/a,年度公用工程费用增加320632USD/a。如图15 所示,HE1、HE2 停用时的公用工程能耗为7.91×10kJ/d,HE5 停用时的公用工程能耗为5.7×10kJ/d。HE1、HE2、HE5 每年都需要停用6天,则因停用所需要的额外公用工程费用作为清洗方案的损失费用,清洗方案的损失费用为87806USD/a。清洗成本为6793USD/a,该清洗方案下年度总费用增加415411USD/a。与不清洗的原始网络额外增加的公用工程能耗和额外增加的公用工程费用相比,年度额外公用工程能耗下降58%,年度额外公用工程费用减少58%,年度额外总费用减少45.6%。
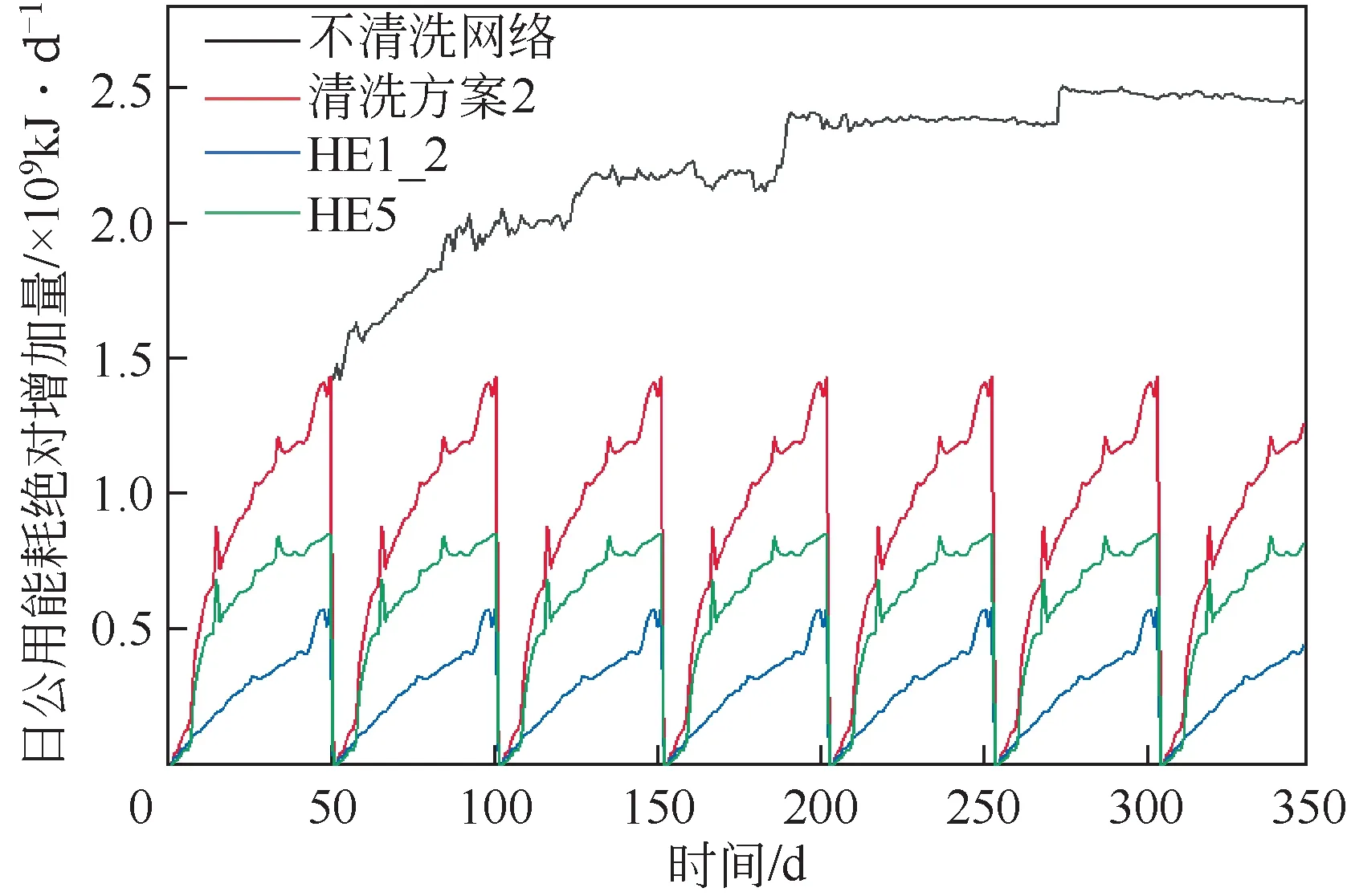
图14 当换热器网络性能衰退10%、停用24h的清洗方案
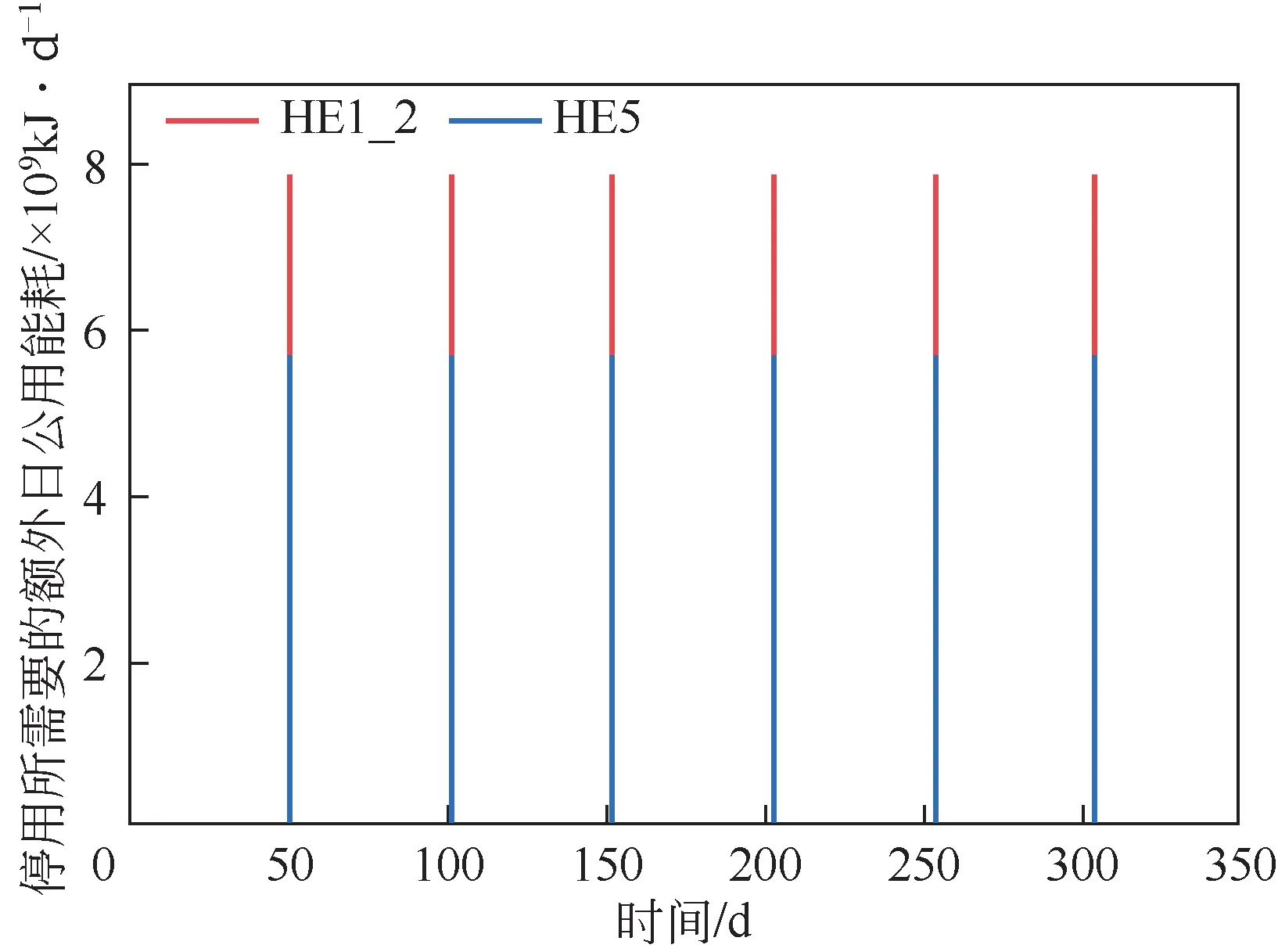
图15 HE1、HE2和HE5停用24h网络需要的额外公用工程能耗
以上两种清洗方案分别代表了两种不同的应用场景下,提高现役换热器运行性能的清洗方案,换热器停用清洗时间为24h。从图16中可以看出,与清洗方案1相比,清洗方案2的年度额外公用工程费用减少13.1%,损失费用减少14.1%,清洗次数增加3台次,清洗费用增加8.1%,但年度总费用减少13.8%。这主要是因为基于单台换热器性能衰退幅度制定的清洗方案1,换热器运行周期较长,换热器长时间处在较差的运行性能,导致换热网络的额外公用工程能耗较多,额外公用工程费用较高,清洗次数较少,清洗费用和由于停用清洗所带来的损失费用较少。由于换热网络性能的整体变化要比单台换热器性能变化更显著,监测网络性能变化,不仅可以实现对单台换热器性能的监测,同时可以反映不同换热器性能衰退对网络性能的影响。因此,根据换热网络性能衰退幅度制定清洗方案较传统的清洗方案具有更好的经济优势。
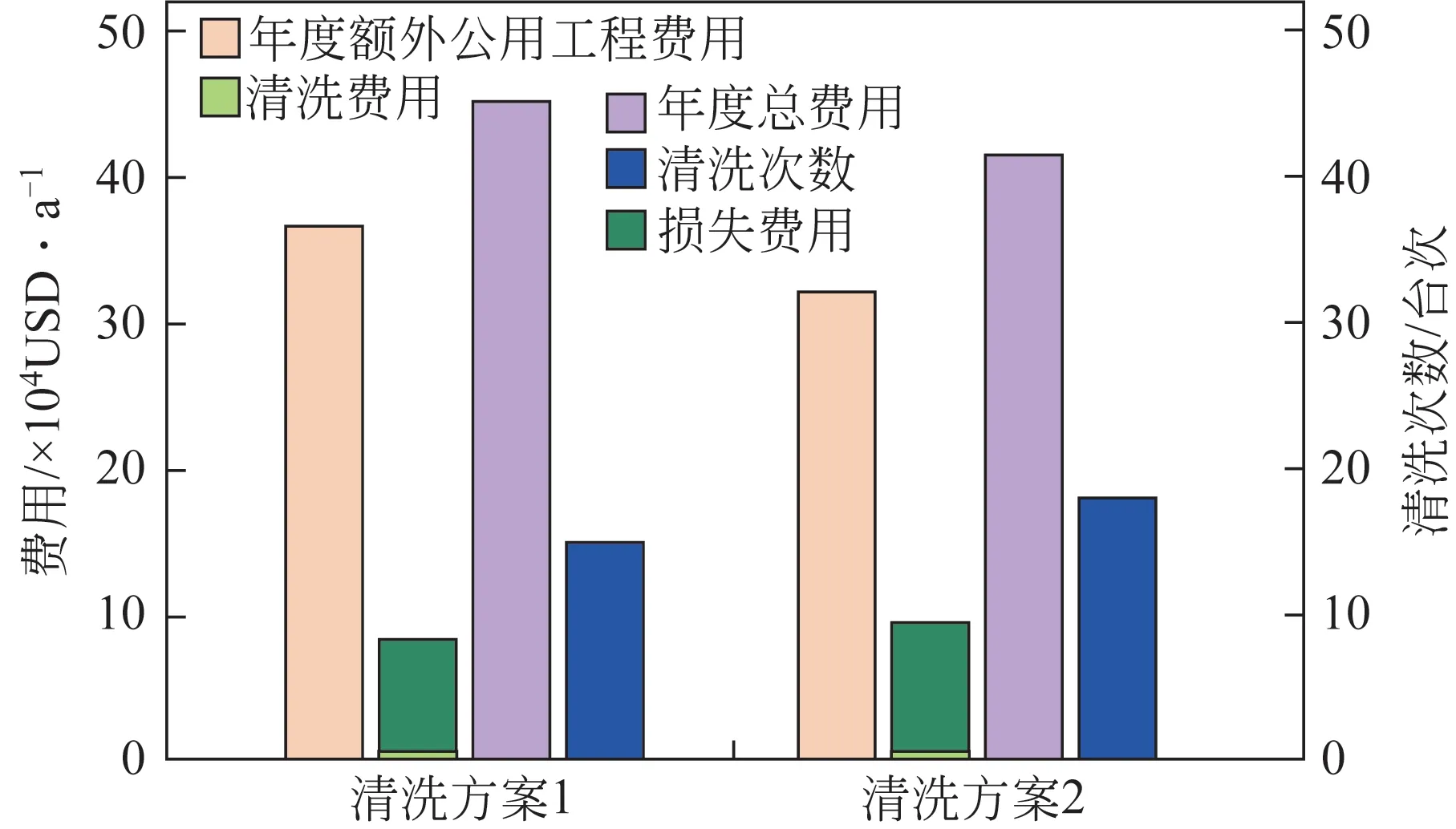
图16 两种方案之间的比较
5 结论
本文针对原油精馏单元的换热网络,从换热网络集成的角度,根据网络中各台换热器性能变化获得换热网络的整体性能变化,提出基于智能预测和机理模型的换热网络性能预测方法;在此基础上开展清洗决策,并开展了相应的案例研究,讨论分析网络性能变化和不同清洗准则下清洗方案的优劣,主要得到了以下结论。
(1)对原油换热器性能的预测,采用污垢阈值模型的经验公式,计算过程较为复杂且结果精度较差。通过对换热器运行数据建立神经网络算法的智能预测模型,可以较好地实现对换热器性能的预测。
(2)换热网络中换热器之间存在耦合关系,不同换热器的性能衰退对换热网络的影响不同,多台换热器同时发生性能衰退时,换热网络的性能衰退要比单台换热器性能衰退更显著。当HE1、HE2和HE5三台换热器都发生性能衰退时,年度额外需要公用工程能耗相对增加高达14.1%,年度额外公用工程能耗费用相对增加12.1%。
(3)与传统基于单台换热器性能衰退制定的清洗方案相比,根据换热网络整体性能衰退制定的清洗方案,年度额外公用工程费用减少13.1%,损失费用减少14.1%,年度总费用减少13.8%,而清洗次数仅增加3台次。
—— 换热面积,m
—— 热容流率,kW/℃
CU—— 冷公用工程
—— 活化能,kJ/mol
HE—— 换热器
HU—— 热公用工程
LMTD—— 对数平均温差,℃
MAE—— 平均绝对误差
MSE—— 平均方差
—— 压强,Pa
—— 普朗特数
—— 热负荷,kW
—— 气体常数,J/(mol·K)
R—— R差
—— 污垢热阻,m·K/kW
—— 雷诺数
RMSE—— 均方根误差
—— 冷物流进口温度,℃
—— 冷物流出口温度,℃
—— 薄膜温度,K
—— 热物流进口温度,℃
—— 热物流出口温度,℃
—— 管壁温度,K
—— 总传热系数,kW/(m·℃)
—— 时间,s
—— 平均流速,m/s
—— 结垢模型中的常数
—— 结垢模型中的常数
—— 结垢模型中的常数
—— 管壁剪应力,Pa
下角标
C—— 冷物流
H—— 热物流
w—— 管壁物理量
f—— 结垢条件下评估的物理量

