巨型星座覆盖性的高效分析方法

吕林立，肖歆昕，冯冠华，李文皓,*

1. 中国科学院 力学研究所，北京 100190 2. 中国科学院大学 工程科学学院，北京 100049

随着商业航天的蓬勃发展，巨型星座网络近年来在建设、组网、服务等多方面取得快速进展。例如，美国SpaceX公司的星链(Starlink)计划部署40 000多颗卫星，目前已经部署了超过1 300颗，超过了其他低轨卫星在轨数量的总和，其他如美国的Kuiper计划、英国的OneWeb、中国的“鸿雁”“鸿云”以及各类部署组网的Telesat和Galaxy Space计划等。

在巨型星座之前，对地和对天覆盖性已经得到了广泛研究，并用于对地观测分析(如NASA的EOS计划)、空间机器人遥操作的中继分析等。对于巨型星座网络，其主要预期服务包括：对地观测、天基互联网通讯服务等。这些服务的实现要求对地有效覆盖、星间有效互联，因此巨型星座的对地、对天覆盖性准确分析是其产生预期能力的前提。此外，巨型星座的建立需要多次部署，逐渐组网，包括建设和服务的过程中，也存在因部分卫星失效而产生补网需求，因此，动态和高效地分析巨型星座的覆盖性非常重要。其计算效率直接影响着星座的设计效率。用于覆盖性分析的覆盖带法，仅能分析圆轨道星座，基于三角剖分的覆盖性分析方法，该类方法仅能分析较简单覆盖区域，也有基于映射的二维图法。对于复杂星座构型，由于星座的覆盖性能难以用解析的方法求解，网格法为广泛使用的方法。网格法最早由Morrison提出，该方法的基本思路是将目标区域的包围盒按经纬度、距离、面积等方式划分为网格，以网格中心点代表网格，按给定步长计算卫星空间位置极点，由地心角法计算并记录卫星对网格点的覆盖情况。

由于网格法的分析是对星座中的各个卫星，均逐个网格遍历求解，因此随着星座中卫星数量的增加，其覆盖性计算的消耗必然会上升，对于10，甚至10量级的星座，使用网格法的覆盖性分析对计算能力和计算效率的需求会直线上升。

本文提出一种覆盖性分析方法：并行墨卡托投影图叠加法(PMPS)，该方法将星座在指定空间天球的覆盖域，通过图像畸变投影至二维墨卡托图上，使用图像面元并行赋值和图像叠加原理，分析星座覆盖性，从而高效提升巨型星座多重覆盖性的分析效率。

1 卫星覆盖模型

1.1 星地覆盖模型

假设地球为正球体，卫星对地覆盖不考虑距离约束，则星座中的单颗卫星对地覆盖域在地球表面为以星下点为圆心的球冠，覆盖模型如图1所示。

图1中，设为卫星对地通讯/观测视场半锥角;为地球半径;为卫星当前轨道高度，则卫星覆盖域对应半地心角′，以及覆盖域球面半径′满足

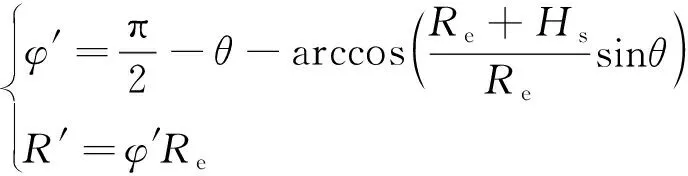
(1)

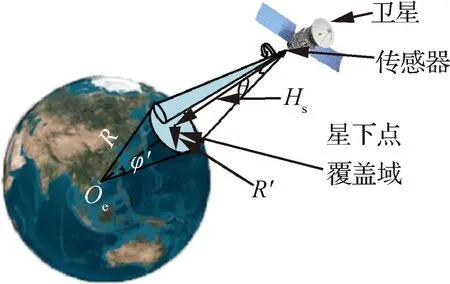
图1 单星对地覆盖模型示意图Fig.1 Single satellite to ground coverage model

1.2 同高度卫星的星间覆盖模型

星间覆盖主要考虑地球曲率遮挡和大气影响，对于同轨道高度的卫星，单颗卫星在同轨道高度空间天球上的覆盖域为以该卫星为圆心的球冠，如图2所示。根据球面几何关系，该球冠对应的半地心角″，以及球面半径″满足

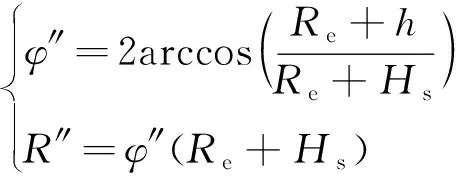
(2)

式中：为大气层厚度。

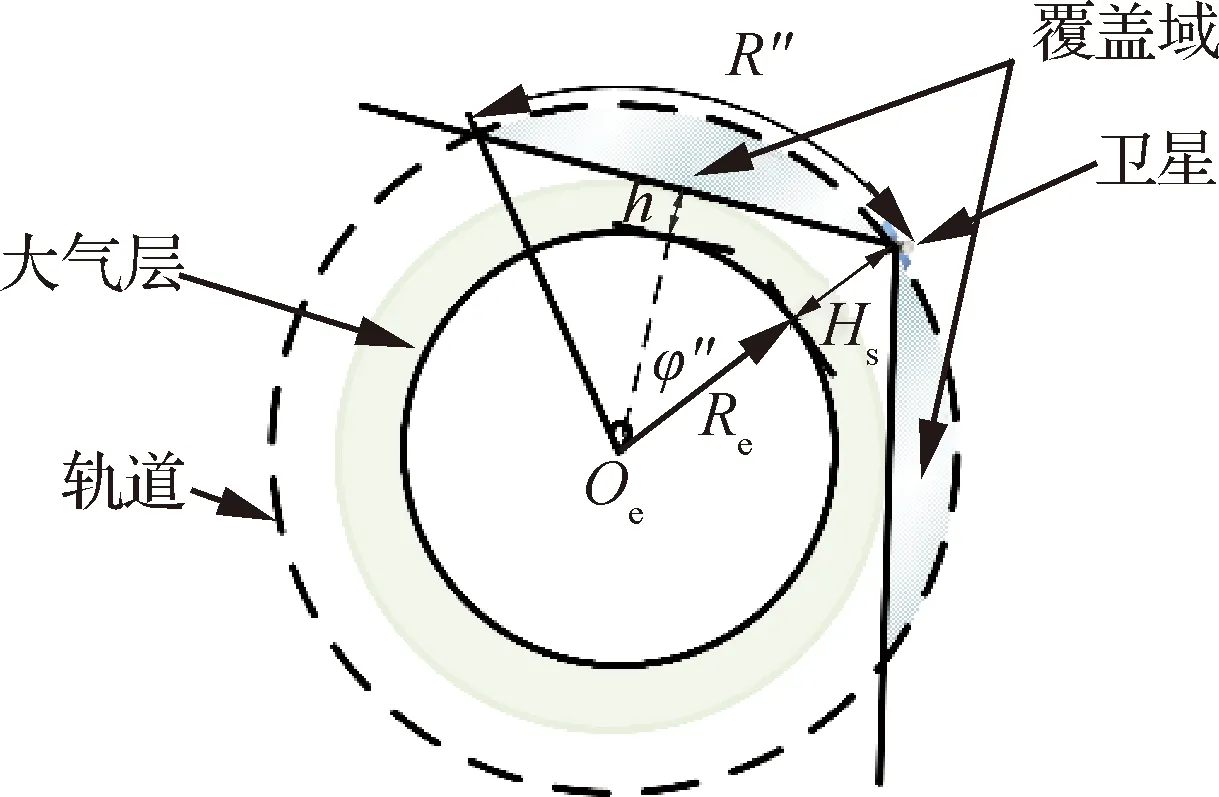
图2 同高度星间覆盖示意图Fig.2 Inter satellite coverage on same height

2 PMPS覆盖性分析方法

PMPS方法具体步骤为

以选定色值初始化给定分辨率墨卡托底图。

单星覆盖域边界空间几何关系曲线计算。针对星座中任一颗卫星，根据式(1)或式(2) 计算其覆盖域边界空间几何关系曲线。

单星覆盖图获取。将空间几何关系曲线进行墨卡托投影，并对区域内的像元进行批赋值，获取其对地、对天覆盖区域。

遍历获取覆盖图。按照步骤2和步骤3遍历获取所有卫星的对地、对天覆盖图。

星座覆盖图获取。通过给定透明度和色值编码方式，依次叠加步骤4所获取的单星覆盖图至墨卡托底图。

星座覆盖性分析。基于图像叠加原理和并行处理算法，对星座覆盖图处理分析获得覆盖性矩阵。结合目标区域的权重矩阵和面积矩阵，获取大规模层叠后的全星座覆盖性分析结果。

2.1 墨卡托覆盖图

定义墨卡托覆盖图(简称：覆盖图)为星座内各卫星在地面或天球上覆盖域的墨卡托投影叠加图。

2.1.1 单星覆盖图

图3为单颗卫星(=1,2,…,)对地覆盖图。

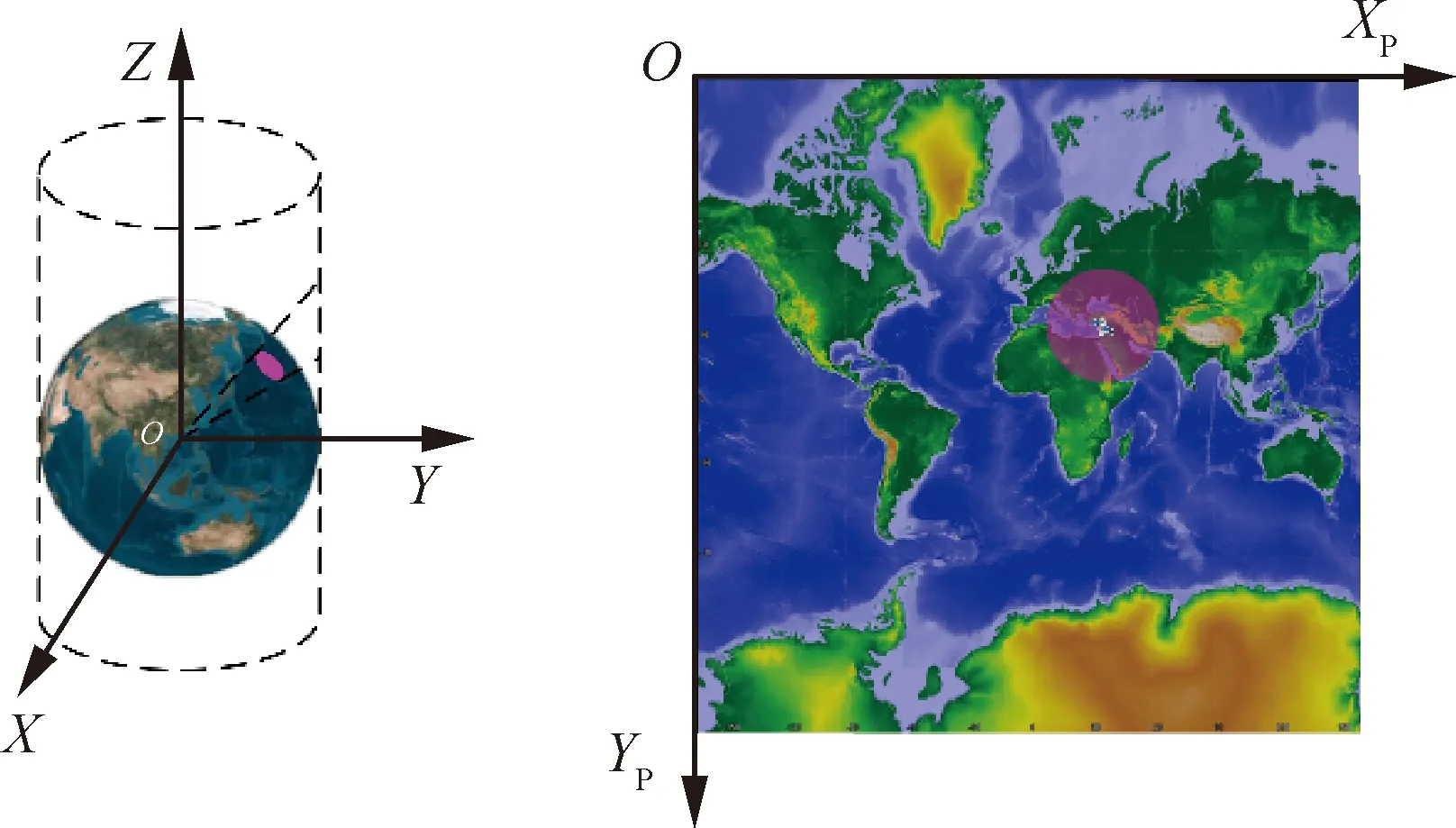
图3 单星覆盖图Fig.3 Coverage of single satellite

由式(1)或式(2)可求得相应覆盖模型下覆盖域球面半径。采用大地主题正解算法，解算以星下点为圆心的覆盖域空间几何关系曲线。选定色彩模型(如三原色光模型(RGB)、印刷四分色模型(CMYK)等)及色值进行图像渲染，获得卫星的覆盖图(=1,2,…,)，为卫星数量。编码方式满足

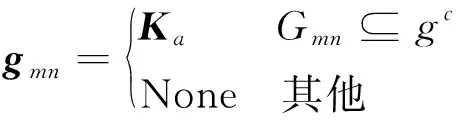
(3)

式中：为覆盖域内像元。

2.1.2 星座覆盖图

以选定的透明度将各卫星的覆盖图逐个叠加，其中将色值″叠加至′获得的叠加原理如式(4)，由此得星座覆盖图。

=(1-)′+α″

(4)

由式(4)可知星座覆盖重数与覆盖图色值一一对应。

2.1.3 各重覆盖矩阵

式(4)可给出重覆盖对应的色值(=1,2,…)，根据和星座覆盖图定义各重覆盖矩阵(=1,2,…)，赋值方法为

(5)

2.2 星座覆盖性分析

各重覆盖面积及各重覆盖率是衡量星座覆盖性的重要指标。本文就这2类覆盖性指标应用PMPS方法进行求解。

2.2.1 面积矩阵

定义维面积矩阵，其各元素为星座覆盖图中，各像元实际地理面积。由墨卡托投影特点可得矩阵：

(6)

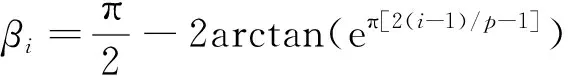
(7)

式中：为覆盖域球面半径；=为图像分辨率；为星座覆盖图第行像元对应地理纬度。

2.2.2 目标域权重矩阵

定义维目标域权重矩阵，中元素的位置包含于目标区域内时，为1，否则为0。满足

(8)

式中：为第行列元素。

2.2.3 覆盖面积与覆盖率

定义为目标区域重覆盖面积，满足

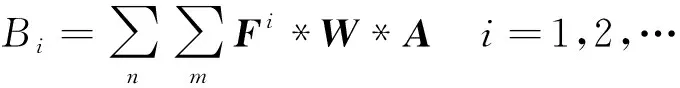
(9)

式中：*为哈达玛积。

定义为目标区域重覆盖率，满足

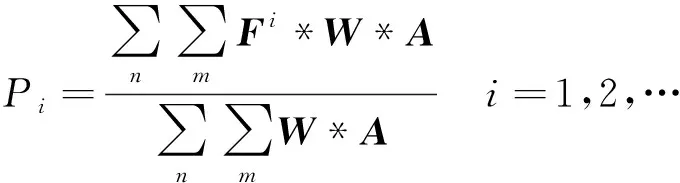
(10)

2.3 算法实现

本文算法实现包括如下几个步骤：

初始化。

赋值。对星座参数，图像叠加透明度、地球半径、目标时刻等参数进行赋值。

卫星轨道外推。

星下点求解。

单星覆盖图投影叠加。

计算覆盖率及覆盖面积输出结果。由式(9)、式(10)计算出覆盖面积及覆盖率，并输出结果。

具体算法流程如图4所示。

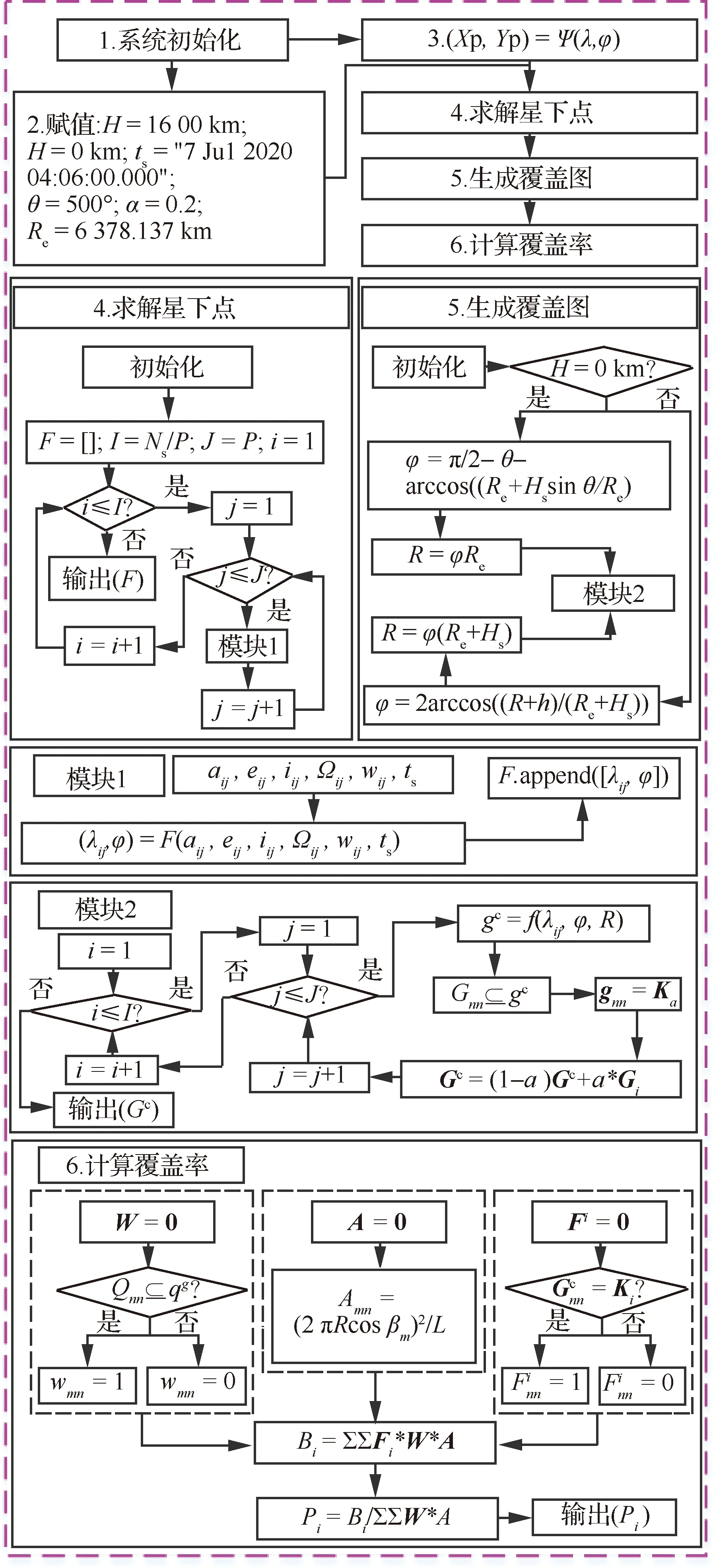
图4 PMPS流程图Fig.4 Flow chart of PMPS

3 计算消耗分析

3.1 GPA计算消耗

GPA的计算过程主要分为3步：

1) 网格点划分。

2) 对个网格点、颗卫星进行逐点逐星覆盖判定。

3) 统计分析结果。因此，其计算消耗′满足

′=′+′+′

(11)

式中：′为网格划分计算消耗；′为单星单点覆盖性判定计算消耗；′为统计分析计算消耗。

由式(11)乘积项′可知，GPA网格点数与卫星数量的乘积影响了算法计算消耗。在给定网格点数下，GPA算法中′、′两项为定值，而′项随着卫星数量变化线性增长。

3.2 PMPS计算消耗

PMPS分析过程主要分为2步：

1) 对颗卫星逐星求解覆盖域并叠加至初始化的墨卡托底图。

2) 统计分析覆盖率。

设为单星覆盖域空间几何关系曲线计算时间消耗，该值为常数，为空间几何关系曲线墨卡托投影时间消耗，该值为常数。设单星覆盖域内像元纵坐标最大值、最小值间差值为，则基于扫描线法的覆盖域内色彩空间编码赋值时间消耗a()=，其中为线填充效率当量；设单星覆盖域边界像元数量为，则基于边界的区域布尔叠加时间消耗b()=，其中为布尔运算效率当量。单星覆盖域求解计算消耗″满足

″=++a()+b()=+++

(12)

式中：、均为常数；a()、b()项与图像分辨率有微弱关联。

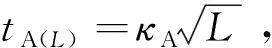
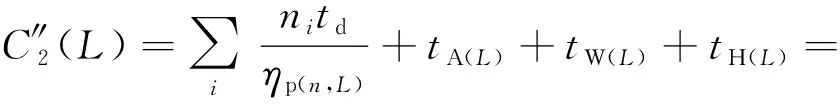
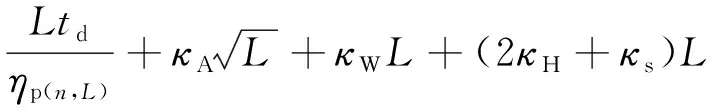
(13)

式中：(=0,1,…)为重覆盖像元数;p(,)为图像并行处理加速比，其理论值可由Amdahl定律给出，在数字图像处理领域，多核环境下的并行加速比已被广泛研究。本文后续算例中，用未引入并行计算的PMPS算法时间消耗与GPA对比分析，也即p(,)=1，因此，并行算法对效率影响本文暂不做详细讨论。

根据上述过程，PMPS计算时间消耗″满足

″=″()+″+″()

(14)

式中：″()为初始化墨卡托底图时间消耗，该值受图像分辨率影响。

因此：

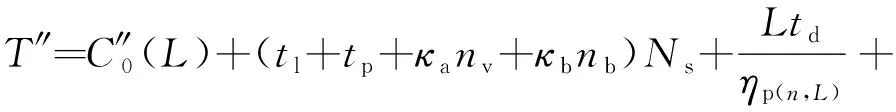
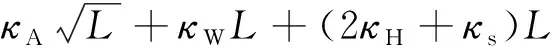
(15)

由式(12)可知，对于给定的覆盖域，单星覆盖域的计算消耗″为常数，式(14)中″项随着卫星数量线性增长。由式(13)可知，给定计算器核数下，覆盖分析时间消耗″()与图像分辨率相关，当图像大小确定时，″()、″()为常数。式(14)可知，PMPS算法中卫星数量和图像分辨率对计算消耗的影响相互独立，该算法突破了计算精度与星座卫星数量的关联约束。

GPA与PMPS计算消耗比值满足式(16)，该值反映了PMPS计算效率比GPA提高的倍数。

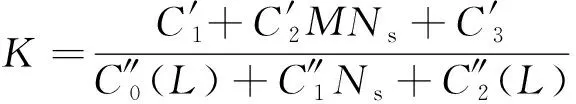
(16)

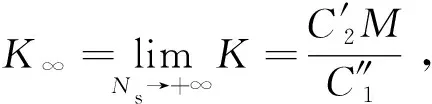
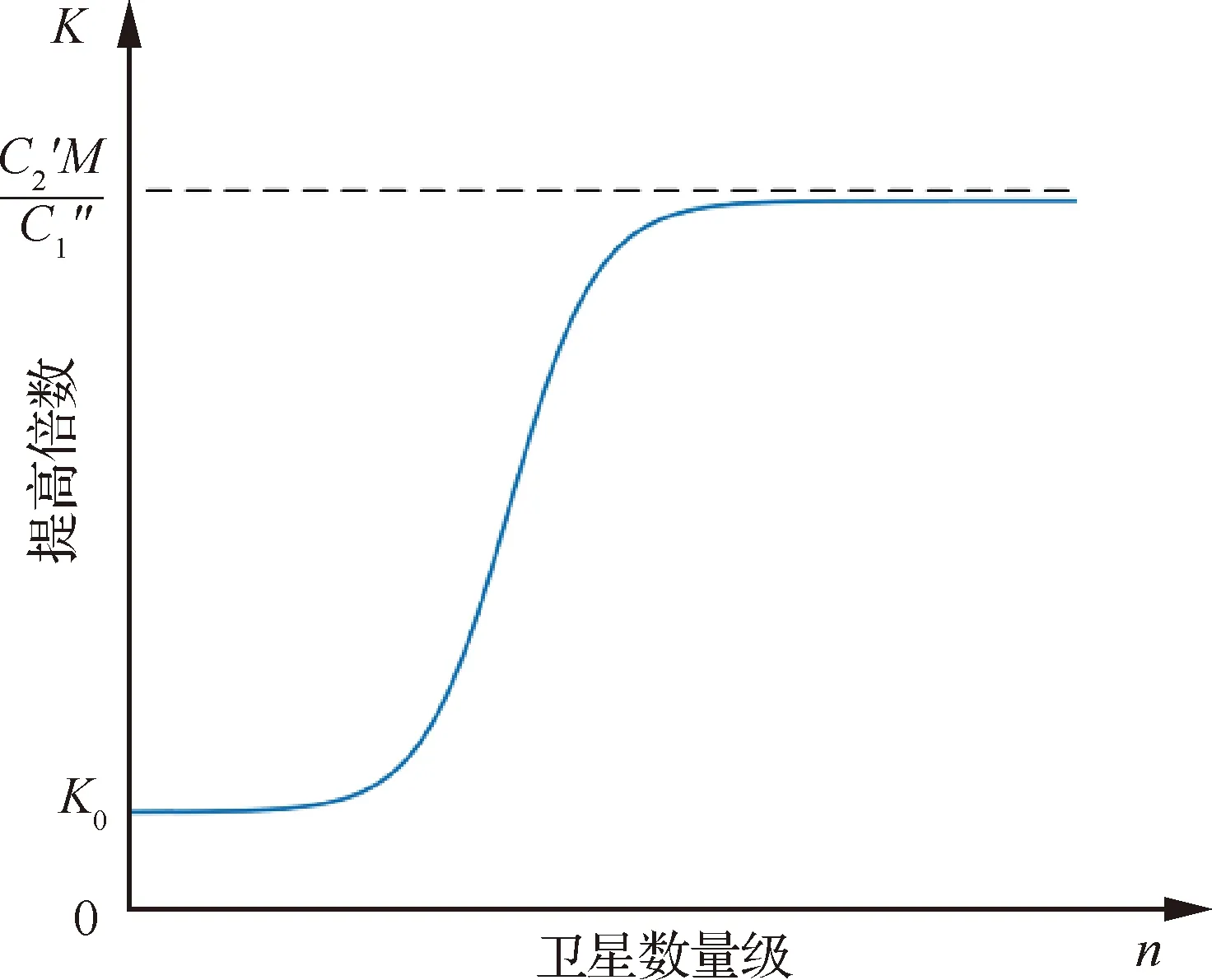
图5 提高倍数与卫星数量级关系曲线Fig.5 Relation curve between multiple of increase of K and order of magnitude of number of satellites

未引入并行计算的PMPS方法不一定比GPA有明显优势。

4 仿真校验

本实验中计算机CPU为Intel(R)Core(TM)i7-6700 K CPU@4.00 GHz,运行内存为4 GB,显卡为NVIDIA GeForce GTX 1060 6 GB，操作系统为Windows 10 64 Bit，开发语言为Python3.7。用未引入并行计算的PMPS算法时间消耗与GPA进行对比分析。

由于传统网格法计算精度随网格数量增加逐渐提高，校验前先确定给定计算精度下GPA网格数量及PMPS图像分辨率。该过程基于对构型为1 584/24/1的Starlink子星座计算结果完成。卫星天线扫描半锥角设为40°，轨道倾角为53°，轨道高度为550 km。

确定计算精度后，算例1对现有典型星座或其子星座进行仿真实验，研究未引入并行计算的PMPS算法与GPA算法间计算误差及计算消耗；算例2在Starlink子星座基础上进行构型变化，研究卫星总数量恒定、星座构型变化下2种算法间的计算误差及计算消耗；算例3采用Starlink的种子卫星参数进行卫星数量变化，研究卫星数量变化下2种算法间的计算误差及计算消耗。本仿真校验中均采用Walker星座，构型为，其中为卫星数量，为轨道平面数，为相位因子。

4.1 计算精度确定

本文采用移动方差法确定GPA计算结果趋于稳定时的网格数。取移动方差窗口步长为5，直至方差小于0.1认为计算结果趋于稳定。结果见表1。并对选定网格数进行网格无关性验证，结果见表2。在确定GPA计算精度后，逐渐提高PMPS中覆盖图分辨率，将计算结果和GPA结果进行对比，两者结果相对误差在5%以内时，认为满足精度要求，结果见表3。

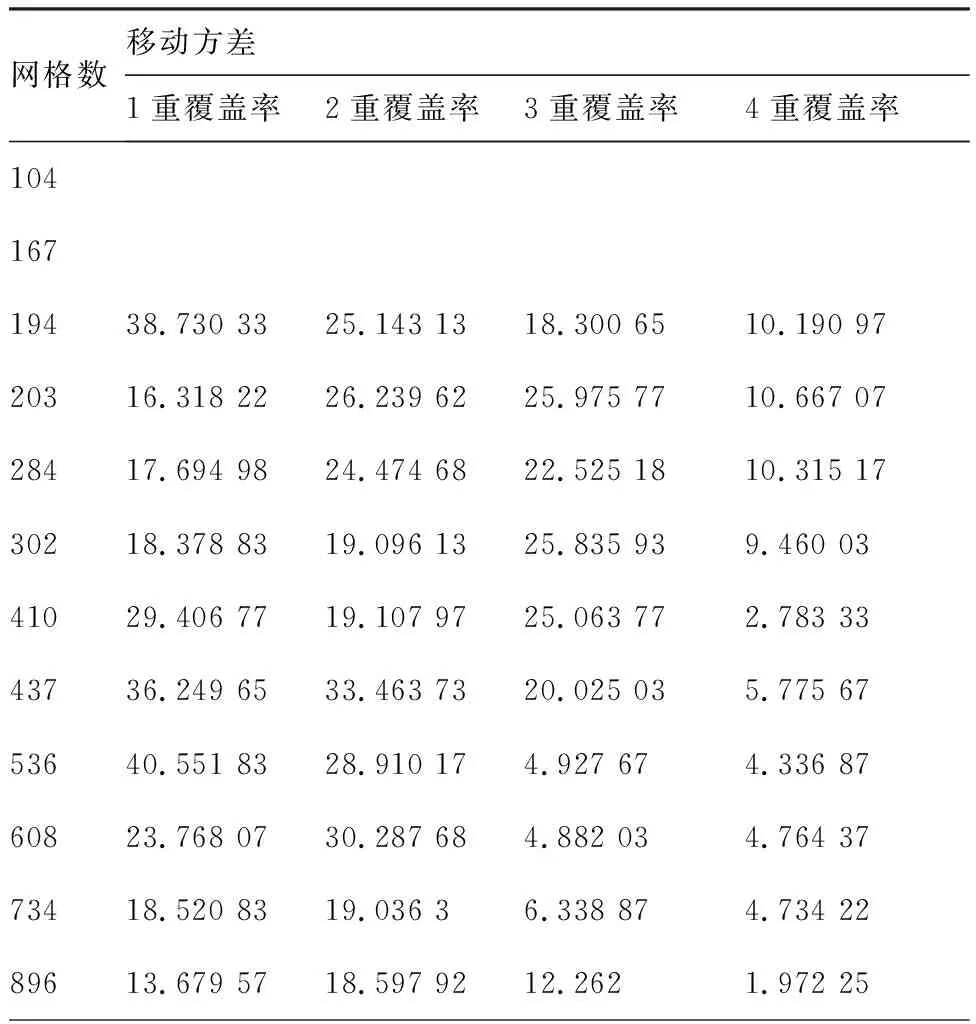
表1 移动方差Table 1 Moving variance

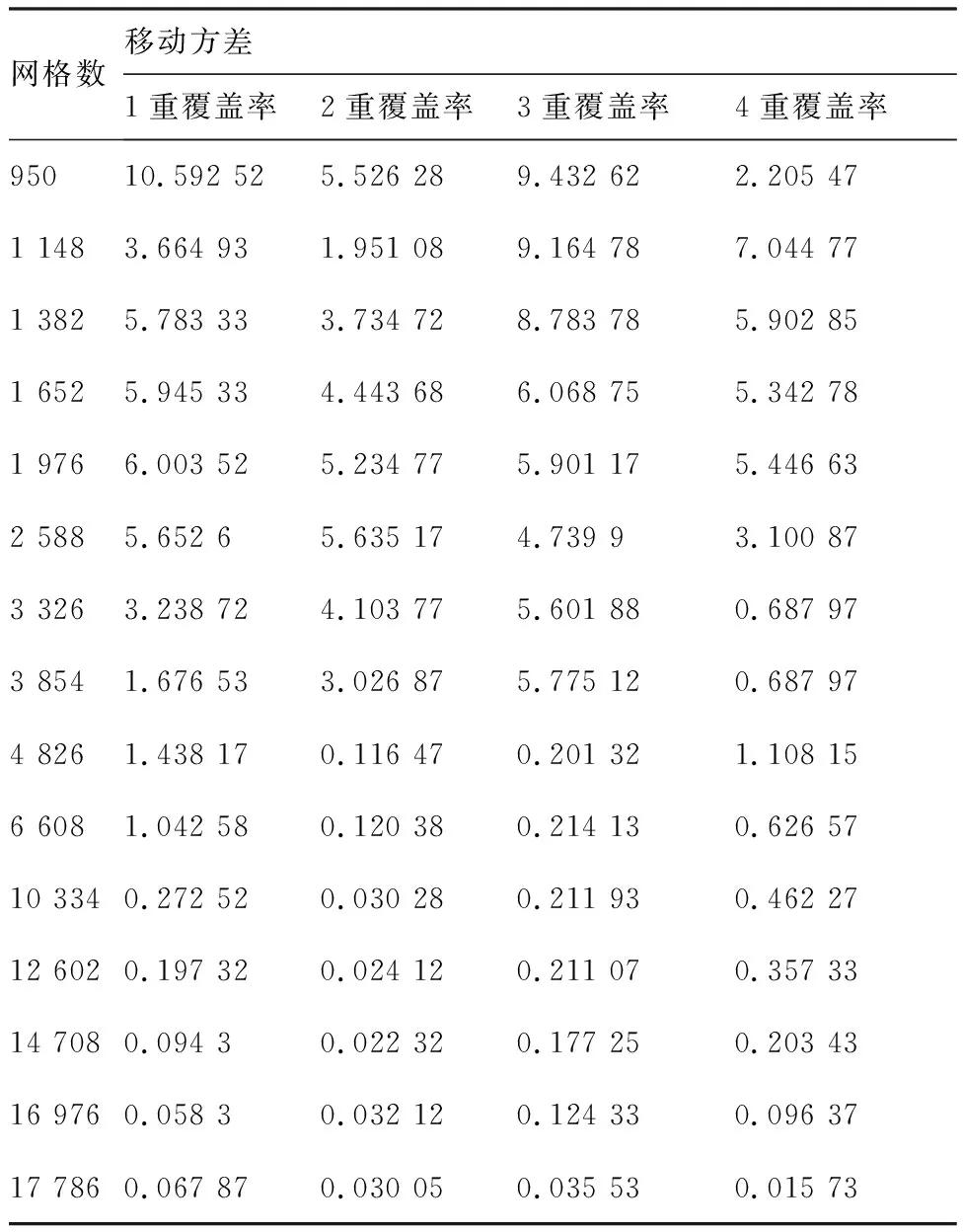
续表1

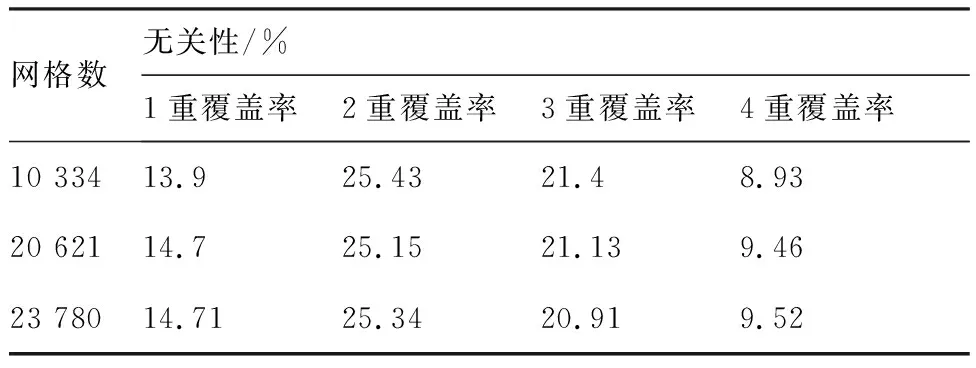
表2 网格无关性验证Table 2 Grid independence verification

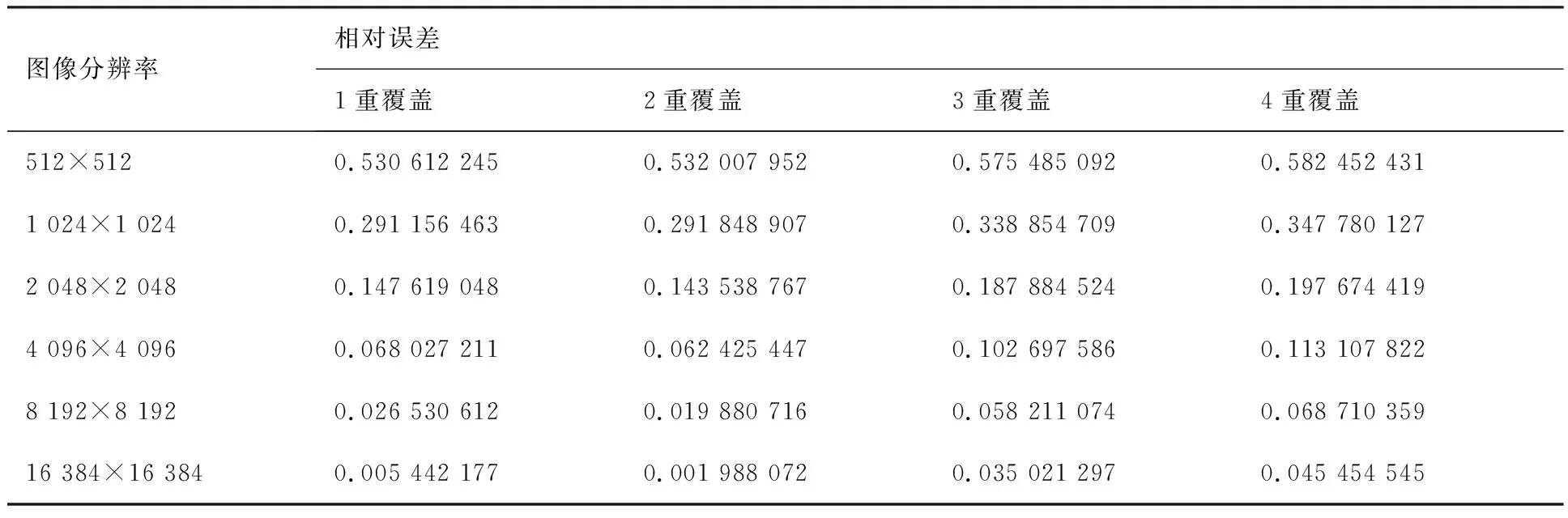
表3 PMPS与GPA相对误差Table 3 Relative error of PMPS and GPA

4.2 仿真算例

对现有星座的计算误差及计算消耗

在现有典型星座或其子星座覆盖性分析算例中，仅考虑物理遮挡因素下的全球覆盖性。星座参数见表4。未引入并行计算的PMPS与GPA分别计算星座对地全球1～5重覆盖率，算法间误差如图6所示，图中(=1,2,3,4,5)表示重覆盖率误差。2种算法计算消耗见图7。

由图6可知，2种算法计算误差在2%以内。由图7可以看出在不同星座下，未引入并行计算的PMPS计算消耗均在400～500 s范围内波动。本算例中GPA对于数量在10量级内的星座，计算消耗相对较低，卫星数量在10量级时，GPA计算消耗高于未引入并行计算的PMPS，这是由于未引入并行计算的PMPS的消耗项″()与图像分辨率呈正相关，在较大图像分辨率下，″()较大。

星座构型变化的计算误差及计算消耗

表4 现有典型星座或子星座参数

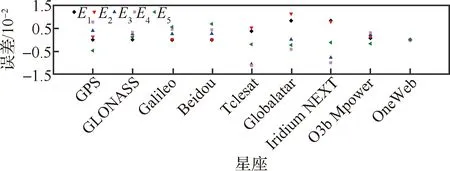
图6 不同星座未引入并行计算的PMPS与GPA间的计算误差Fig.6 Calculation errors between PMPS without parallel computing and GPA for different constellations

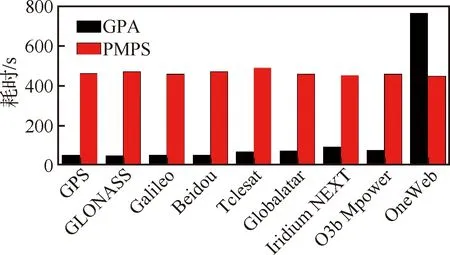
图7 不同星座下未引入并行计算的PMPS与GPA计算消耗Fig.7 Time consumption of PMPS without parallel computing and GPA for different constellations

本算例中取卫星总数量为1 584颗，位于高度550 km的圆轨道，传感器锥角为40°。对表5所示16个构型的星座进行对地全球1～5重覆盖率计算。2种算法间的计算误差见图8，2种算法计算消耗见图9。

由图8可知2种算法的计算误差保持在1%内。由图9可知GPA算法计算消耗在其均值2 492.57 s的2.73%范围内波动，未引入并行计算的PMPS算法计算消耗在其均值514.13 s的2.72%范围内波动，因此可基本排除星座构型对计算消耗的影响。

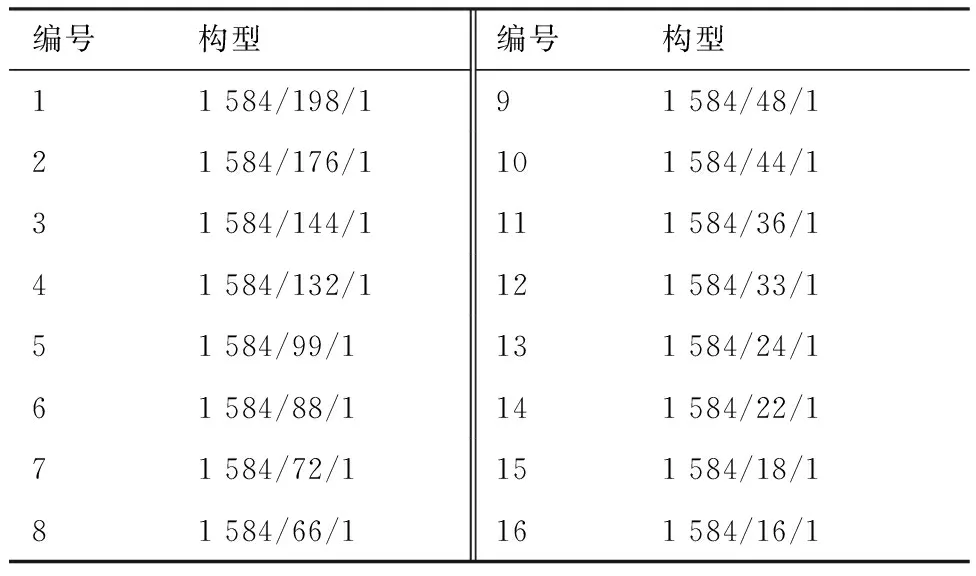
表5 星座构型Table 5 Constellation configurations

图8 不同构型下未引入并行计算的PMPS与GPA间的计算误差Fig.8 Calculation errors between PMPS without parallel computing and GPA for different constellation configurations

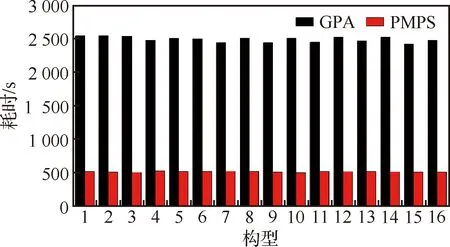
图9 不同构型下未引入并行计算的PMPS与GPA计算消耗Fig.9 Time consumption of PMPS without parallel computing and GPA for different configurations

卫星数量变化下的计算误差及计算消耗

本算例中各Walker星座均采用24轨道面，星座卫星数量由288颗以步长72依次增至1 584颗。具体星座构型见表6。分别用2种算法计算各星座对地全球1～5重覆盖率，计算结果误差如图10所示，计算消耗如图11所示。

由图10可知，2种算法计算各星座1～5重覆盖率误差在2%以内。由图11可知2种算法符合线性增长趋势，对数据进行线性拟合可知，在该计算精度下，GPA计算消耗随卫星数量的增长率为1.643 4，未引入并行计算的PMPS计算消耗随卫星数量的增长率仅为0.027 6，因此未引入并行计算的PMPS计算消耗对卫星数量的敏感度明显低于GPA。

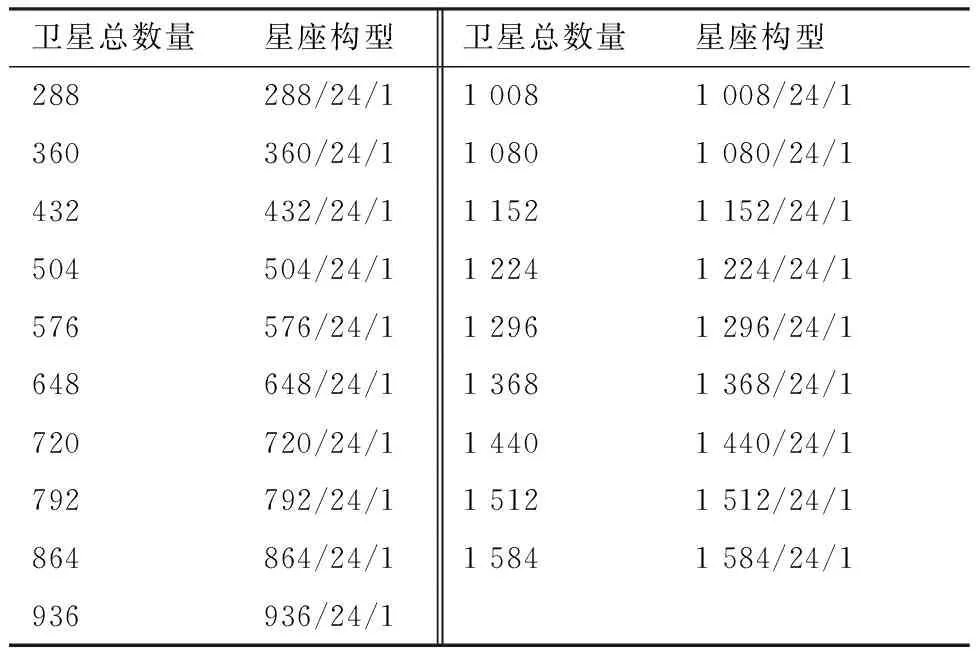
表6 卫星数量及其星座构型

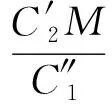
图10 不同卫星数量下未引入并行计算的PMPS与GPA间的计算误差Fig.10 Calculation errors between PMPS without parallel computing and GPA for different number of satellites

图11 不同卫星数量下未引入并行计算的PMPS与GPA计算消耗比较Fig.11 Time consumption of PMPS without parallel computing and GPA for different number of satellites

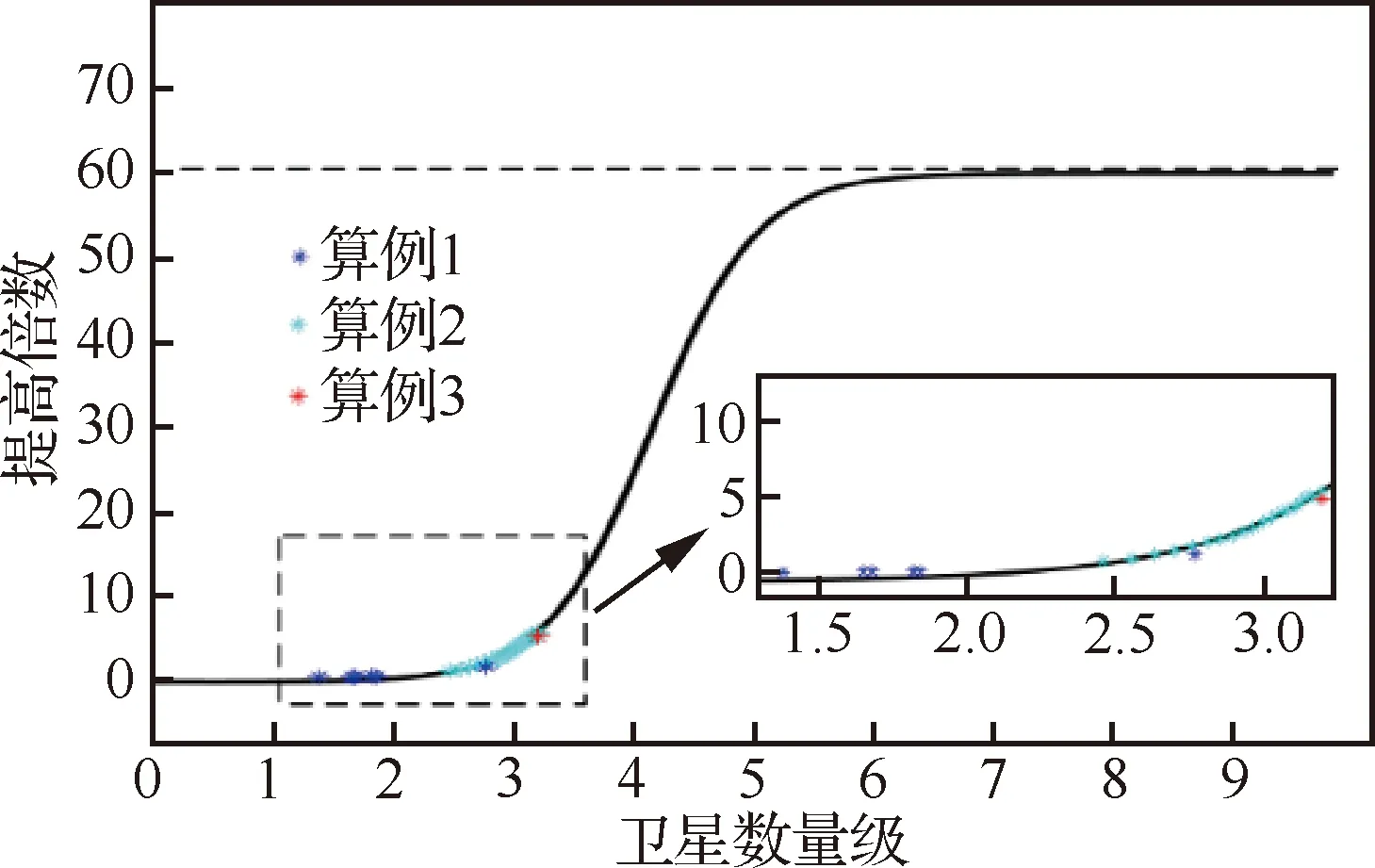
图12 给定精度下未引入并行计算的PMPS相对GPA提高倍数与卫星数量级关系曲线Fig.12 Relation curves between multiple of increase and order of magnitude of number of satellites of PMPS without parallel computing relative to that of GPA at given accuracy

5 结 论

提出一种高效的星座覆盖性分析方法PMPS，通过计算效率的理论分析，及现有星座和构型参数变化下的星座计算分析得出以下结论：

1) 给定计算精度下，随着卫星数量的增加，GPA与未引入并行计算的PMPS计算消耗比值逐渐增加，并最终趋于极限值，由式(16)该极限值和GPA计算精度选取呈正相关。

2) 在GPA网格数为10量级、2种算法计算误差小于2%时，未引入并行计算的PMPS计算效率比GPA最大提高1～2个量级，当GPA网格数量更大时，如10量级，该计算效率将提升2～3个量级。

3) 后续选择合适的处理器核数、引入图像压缩技术，将降低PMPS计算精度对计算消耗的影响系数，有效减小式(14)中″()项。使PMPS计算效率相较于GPA在较小量级星座下便开始提高。

4) 本文工作可以为其他覆盖计算方法的设计提供参考，为解决星座设计问题和星座调度问题提供依据。