基于子结构法与损伤识别的周期性结构脆性断裂相场模拟

王博臣，侯玉亮，夏凉,*，史铁林

1.华中科技大学 数字制造装备与技术国家重点实验室，武汉 430074 2.郑州大学 机械与动力工程学院，郑州 450001

断裂是材料的主要破坏形式之一，断裂的模拟在科学研究和工程应用中具有十分重要的意义，同时也极具挑战性。在航空领域，飞行器复杂的服役环境以及设计、制造过程中形成的缺陷、微裂纹导致结构强度降低。为检验结构强度是否满足设计性能指标，需要对在研飞行器进行强度校验，包括地面强度试验和断裂数值模拟等验证性措施；其中，对断裂数值模拟的有效性提出了苛刻的要求。材料断裂的相关研究经历了多个阶段的发展，最早可以追溯到Griffith的相关工作，他通过弹性应变能和裂纹表面能之间的平衡关系研究裂纹的扩展。在Griffith相关工作的基础上，Irwin建立了线弹性断裂力学，借助连续介质力学的方法研究材料的断裂机制。近几十年来，随着有限元方法和计算机技术的发展，数值断裂模拟方法被广泛应用于断裂研究。基于有限元方法的断裂模型一般可分为2种：分离式裂纹模型和弥散式裂纹模型。

单元删除法是一种典型的分离式裂纹模型，该方法根据单元的应力水平或弹性应变能水平进行判断，将超过材料损伤阈值的单元进行删除；然而，该方法难以模拟裂纹的分叉和复杂裂纹形式。界面单元法在单元之间插入内聚力界面单元，当界面单元的内聚力达到断裂条件时发生失效，裂纹在该界面单元处相应成核或扩展。在界面单元法中，裂纹成核与扩展只允许发生在单元的界面处，模拟结果存在较强的有限元网格依赖性，难以模拟复杂裂纹形式。扩展有限元法采用扩展形函数表示裂纹两侧位移场的间断，裂纹可以在自由度被扩展的单元内部成核与扩展，因此一定程度上避免了网格依赖性问题。由于需要显式地追踪裂纹尖端，扩展有限元法较难被应用于多裂纹扩展、三维问题等复杂断裂问题的模拟。

相场断裂模型是一种弥散式裂纹模型，近年来得到了快速发展。与分离式裂纹模型相比，相场断裂模型通过一个弥散分布的标量场近似描述裂纹，通过求解偏微分方程模拟裂纹成核与扩展，避免了不连续位移场中裂纹几何描述和尖端追踪的难题，极大地简化了算法实现的复杂度，适用于多种复杂断裂问题。相场断裂模型起源于1921年提出的Griffith能量理论。该理论突破了传统的强度理论，通过能量平衡研究裂纹的扩展。1998年，Francfort和Marigo在Griffith能量理论的基础上提出了断裂变分原理，将弹性体的总能量表述为关于弹性体位移场和裂纹分布的泛函，可通过最小化总能量来表征裂纹的成核与扩展。断裂变分原理是对Griffith能量理论的继承和发展，实现了裂纹起裂、分叉等现象的模拟。在断裂变分原理的基础上，Bourdin等进一步引入了一个标量场(相场)对裂纹进行正则化描述，数值上实现了断裂变分原理，称为相场断裂模型。目前，相场断裂模型已被广泛应用于动态断裂、塑性材料、各向异性材料、岩石材料、复合材料、结构优化等领域。

在相场断裂模型中，裂纹弥散宽度由定义的正则化参数()控制，该参数亦可被视为材料相关的本构参数。相场断裂模型要求在裂纹附近进行精细化的有限元网格剖分。Miehe等研究表明裂纹处有限元网格特征尺寸()和正则化参数需要满足关系：≤2。通常情况下，正则化参数与计算区域整体尺寸相比是一个较小的值，将导致规模庞大的有限单元数量。对于裂纹分布已知或可预测的简单断裂问题，通常可在预测的裂纹扩展路径区域进行网格细化，而其他区域采用较粗的网格，控制有限元模型的计算规模。对于裂纹轨迹无法预测甚至可能出现多裂纹交汇的复杂断裂问题，例如复合材料、周期性点阵填充结构等，难以对其裂纹扩展轨迹进行有效先验预测。针对该类断裂模拟问题，需要对全区域进行精细化网格剖分，这对计算能力提出了极高的挑战。针对于此，Burke等发展了残差驱动的自适应网格细化算法，并证明基于该算法的自适应网格使得能量泛函收敛到局部极小值。Patil等基于多尺度有限元方法实现了自适应网格剖分算法，根据断裂相场数值及其增量判断裂尖和裂纹位置，在细网格尺度对裂纹和裂尖进行分析，在粗网格尺度对其余位置进行分析。Ziaei-Rad和Shen实现了相场断裂模型的GPU(Graphical Processing Unit)并行计算，显著降低了求解时间。

针对复杂断裂问题相场模拟计算规模庞大的瓶颈，本文计划基于子结构法和损伤识别，发展适用于周期性结构脆性断裂的高效相场模拟方法。首先，根据周期性特征对结构进行分区，选取特征子域结构进行内部节点的自由度凝聚，生成相应的超单元，并由其组装周期性结构的整体刚度矩阵,降低计算规模。然后，离线(Off-line)对特征子域结构施加拉伸和剪切测试载荷并进行相场断裂模拟，得到子域内部损伤与子域弹性应变能之间的定量关系，标定合适的能量判定阈值。在线(On-line)断裂模拟过程中将仅对阈值以上子域的内部位移和断裂相场进行解耦分析，避免非裂纹扩展子域的重复计算消耗。

1 相场断裂模型

1.1 裂纹正则化

图1(a)为一含裂纹弹性体的示意图：∈、∂∈-1分别为弹性体区域及其边界，∈-1为裂纹；∈{1,2,3}表示空间维度，、、分别表示一维、二维、三维空间；边界分为∂和∂，分别对应Dirichlet和Neumann边界。如图1(b)所示，通过定义一个取值在区间[0,1]的标量相场(,)近似描述裂纹的分布，即裂纹的正则化描述；其中，为该材料点的位置，为加载时间。当相场取值为0时表示材料完好(无裂纹)；相场取值为1时表示材料完全破坏(裂纹)；当相场取值介于0～1时，材料处于完好和完全破坏之间的过渡状态，即弹性体中弥散分布着裂纹。

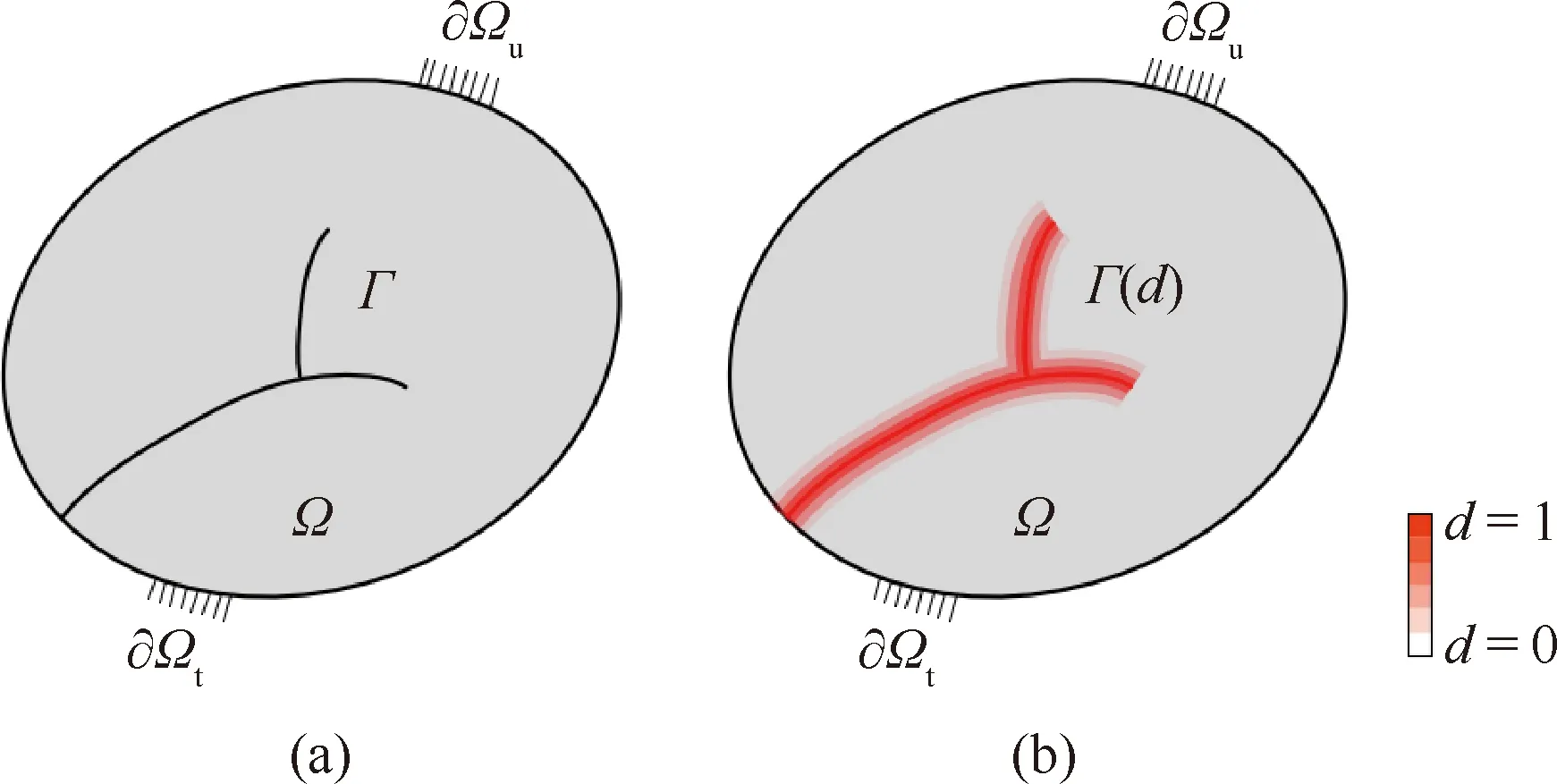
图1 裂纹的正则化表示Fig.1 Regularized representation of crack

满足以上断裂相场条件的标量场可通过求解以下边值问题得到：

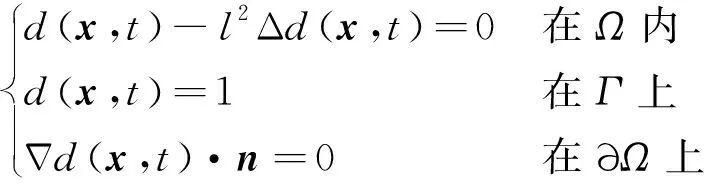
(1)

(2)

边值问题式(1)的欧拉变分形式为

(3)

式中：(,) 满足Dirichlet边界条件

={|(,)=1,在上}

(4)

为裂纹表面函数，计算公式为

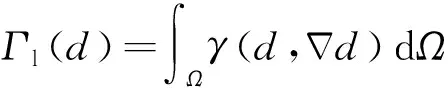
(5)

式中:为弹性体中弥散分布裂纹的密度函数，计算公式为

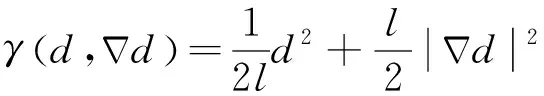
(6)

1.2 控制方程强形式

Francfort与Marigo提出了断裂变分原理，该原理是相场断裂模型的理论基础。断裂变分原理将产生裂纹弹性体的自由能分为弹性应变能和裂纹表面能2部分，裂纹成核与扩展的同时伴随着弹性应变能向裂纹表面能的转换，即弹性应变能和裂纹表面能分别驱动和阻碍着裂纹的成核与扩展：

(7)

式中：为位移；为应变张量；()为弹性应变能密度函数，其在弹性体上积分为弹性应变能；为临界能量释放率,其在裂纹表面上积分为裂纹表面能。由于裂纹位移场的不连续性，且裂尖处存在奇异的应力场，裂纹表面能难以计算。

通过引入相场标量(,)对裂纹进行正则化描述，即由全域弥散分布的裂纹近似描述真实裂纹，弹性体自由能可近似表述为

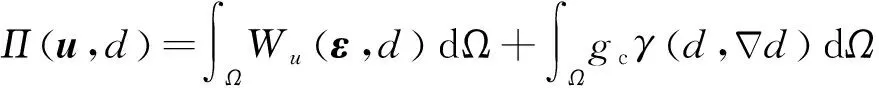
(8)

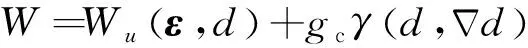
(9)

为防止材料在受压状态下出现裂纹，需要对应变能进行拉压状态分解

()=()+()

(10)

式中：()、()分别为拉伸和压缩部分的应变能。应变能的分解方法有多种，本文基于应变能谱分解方法对其进行拉压分解

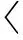
(11)

=+

(12)

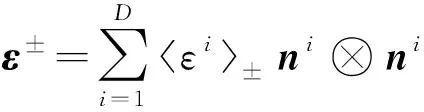
(13)

(,)=[()+]()+()

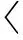
(14)

式中：为引入的一个极小值，用于保证材料完全破坏时单元刚度矩阵的非奇异性；()为弹性应变能退化函数，描述断裂相场对弹性应变能拉伸部分的影响，需满足：

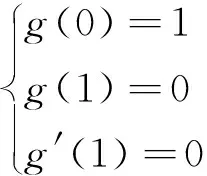
(15)

通常选取

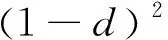
(16)

拉压分解后的弹性体自由能表述为

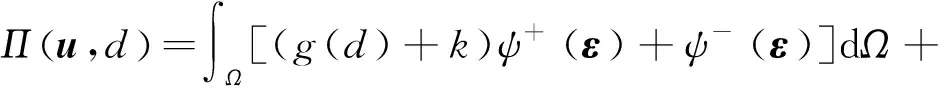
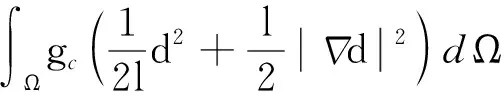
(17)

对式(17)进行位移场和相场的变分可得

(18)

相应边值问题为

(19)

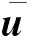
=-Δ

(20)

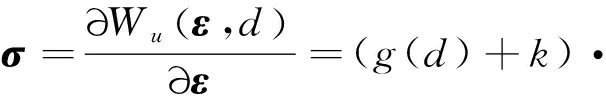
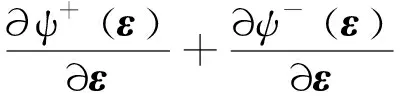
(21)

由于断裂的不可逆性，为防止卸载后裂纹发生愈合，引入历史状态变量H

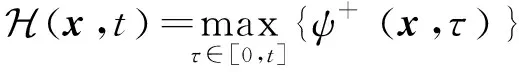
(22)

替代边值问题式(19)中的。

1.3 控制方程弱形式

忽略体力的作用，位移场的弱形式为

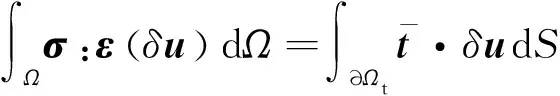
(23)

根据弹性应变能密度的定义，应力计算公式为

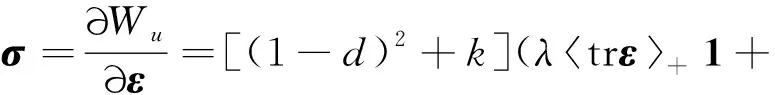
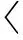
(24)

式中：为二阶单位张量。

将相场控制方程乘上试函数在全域上积分，得到其等效积分形式

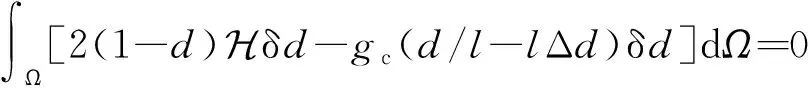
(25)

根据分部积分法则、散度定理，并引入边界条件，可得相场控制方程的弱形式

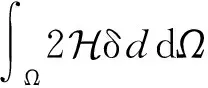
(26)

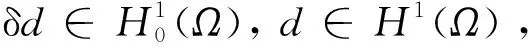
1.4 有限元离散

对位移场和相场进行有限元离散，可得位移场平衡方程和相场演化方程

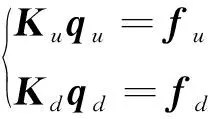
(27)

式中：、分别为位移场和相场的整体刚度矩阵；、分别为位移向量和相场向量；、分别为位移场和相场的外载荷向量。

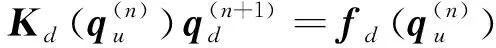
(28)

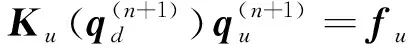
(29)

2 子结构建模及损伤识别

对于周期性结构的断裂模拟，可利用结构的周期性特征，将结构划分为若干几何构型一致的子域，通过子结构法对子域的内部计算节点进行静态凝聚降低计算规模；其后，结合线下测试标定的应变能损伤阈值，判定是否需进一步求解子域的内部响应，避免非必要的计算消耗。

2.1 子结构建模

根据结构的周期性特征，可将其划分成若干几何构型一致的子域。数值上，具有相同几何特征的子域结构的刚度矩阵一致，因此以下某一代表性子域结构的位移或相场的有限元列式为

=

(30)

根据节点是否位于子域的边界上，式(30)可分区域表示为

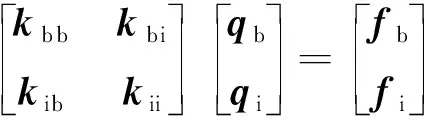
(31)

式中：下标i、b分别表示该自由度对应节点位于子域内部和边界。由式(32)可得

(32)

将式(32)代入式(31)可得

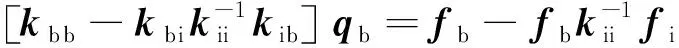
(33)

定义以下矩阵和向量：

(34)

可得边界节点响应的有限元列式：

=

(35)

以上过程称为子结构法静态凝聚。子结构建模的过程如图2所示，具体步骤为：① 对特征子域进行静态凝聚；② 由凝聚的刚度矩阵组装整体刚度矩阵；③ 求解整体结构有限元问题；④ 根据节点响应解耦求解内部响应。

相场断裂模拟为非线性问题，需多次迭代施加载荷，重复以上计算步骤。需要注意的是，若子结构内部出现裂纹，需对该子结构的位移和相场凝聚刚度矩阵进行更新，并重新组装结构的整体刚度矩阵。

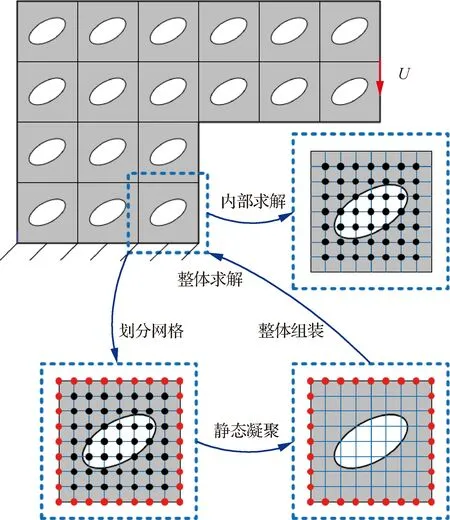
图2 周期性结构的子结构建模Fig.2 Substructuring of periodic structure

2.2 损伤识别

在利用子结构法对周期性结构进行断裂模拟时，若子结构内部无裂纹产生，则无需求解子结构内部的位移场和相场，此类子结构仅需执行一次静态凝聚；而内部产生裂纹的子结构，需进一步求解子结构内部的位移场和裂纹相场。由于裂纹的成核与扩展会引起材料性能的退化，故在每一个加载步中均需对含裂纹子结构重新进行静态凝聚。为判别子结构内部是否有潜在裂纹形成的可能性，需进行子结构的损伤识别。由于每次加载时位移场平衡方程的边界条件发生改变，而裂纹相场演化方程的边界条件保持不变，所以选择利用子结构边界位移响应进行损伤识别。同时，断裂的产生伴随着弹性应变能和裂纹表面能之间的转换，故将通过子结构边界位移响应计算得到的弹性应变能作为损伤识别的指标,计算公式为

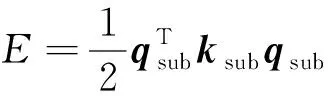
(36)

以二维情况为例，为研究某一代表性子域结构内部损伤与边界位移响应关系，对其施加如图3所示6种典型离线测试工况，其中为位移载荷。若子域结构具有几何对称性，可相应减少测试工况的类型。根据离线测试结果标定该类型子域结构内部发生潜在裂纹损伤的能量识别阈值。

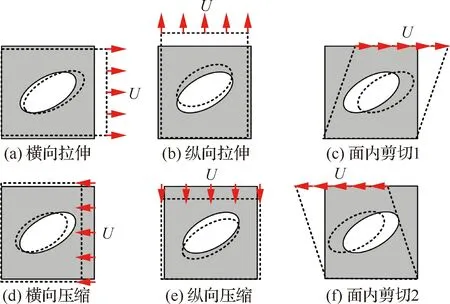
图3 测试工况：横向/纵向的拉伸和压缩,面内剪切Fig.3 Testing loads: Horizontal/vertical tension and compression, and in-plane shear

2.3 算法流程

基于子结构建模和损伤识别，本文发展了一种适用于周期性结构脆性断裂模拟的高效相场方法，其计算流程归纳如下：

将待分析周期性结构进行有限元网格剖分，保证相同特征子域分区的网格形式一致。

对特征子域结构的位移和相场的刚度矩阵进行静态凝聚，组装结构整体刚度矩阵。

对特征子域结构进行离线典型工况测试，标定基于应变能的损伤识别阈值。

施加载荷增量进行在线断裂模拟，根据子结构边界响应计算的弹性应变能进行损伤识别判定：若低于阈值，无需求解内部响应；若高于阈值，求解内部响应，并重新进行静态凝聚。

重新组装位移和相场的整体刚度矩阵，重复步骤4，直至分析完成。

3 数值算例

考虑由方孔单胞周期性排列构成结构的断裂模拟。首先，对方孔单胞进行离线测试，标定损伤识别的能量阈值；随后，基于子结构建模和损伤识别对两类周期性结构进行在线的相场断裂模拟，并与常规相场法的模拟结果和计算规模进行比较。

3.1 方孔单胞离线测试

如图4所示，考虑2种不同尺寸的方孔单胞，分别定义为类型A和B。A和B两类单胞均采用边长=0.005 mm的平面应力四节点正方形单元进行网格剖分。参照文献[31]，脆性材料的参数设置为：=121.5 kN/mm,=80.77 kN/mm，=2.7×10kN/mm；相场模型中的正则化参数设置为=0.015 mm。

由于方孔单胞的几何对称性，可相应简化典型工况的数目；此外，由于相场模型对弹性应变能进行了拉压状态分解，压缩状态的材料难以退化形成裂纹。综合以上因素，仅需考虑纵向拉伸和面内剪切2种工况进行损伤能量阈值的标定。单胞A在加载过程中弹性应变能-位移曲线和裂纹轨迹如图5所示。单胞弹性应变能在加载过程中先逐渐增大，随后在裂纹成核引起材料退化时发生骤降。单胞B在典型工况加载过程中曲线变化趋势和单胞A一致，仅应变能的幅值成比例相应增大。

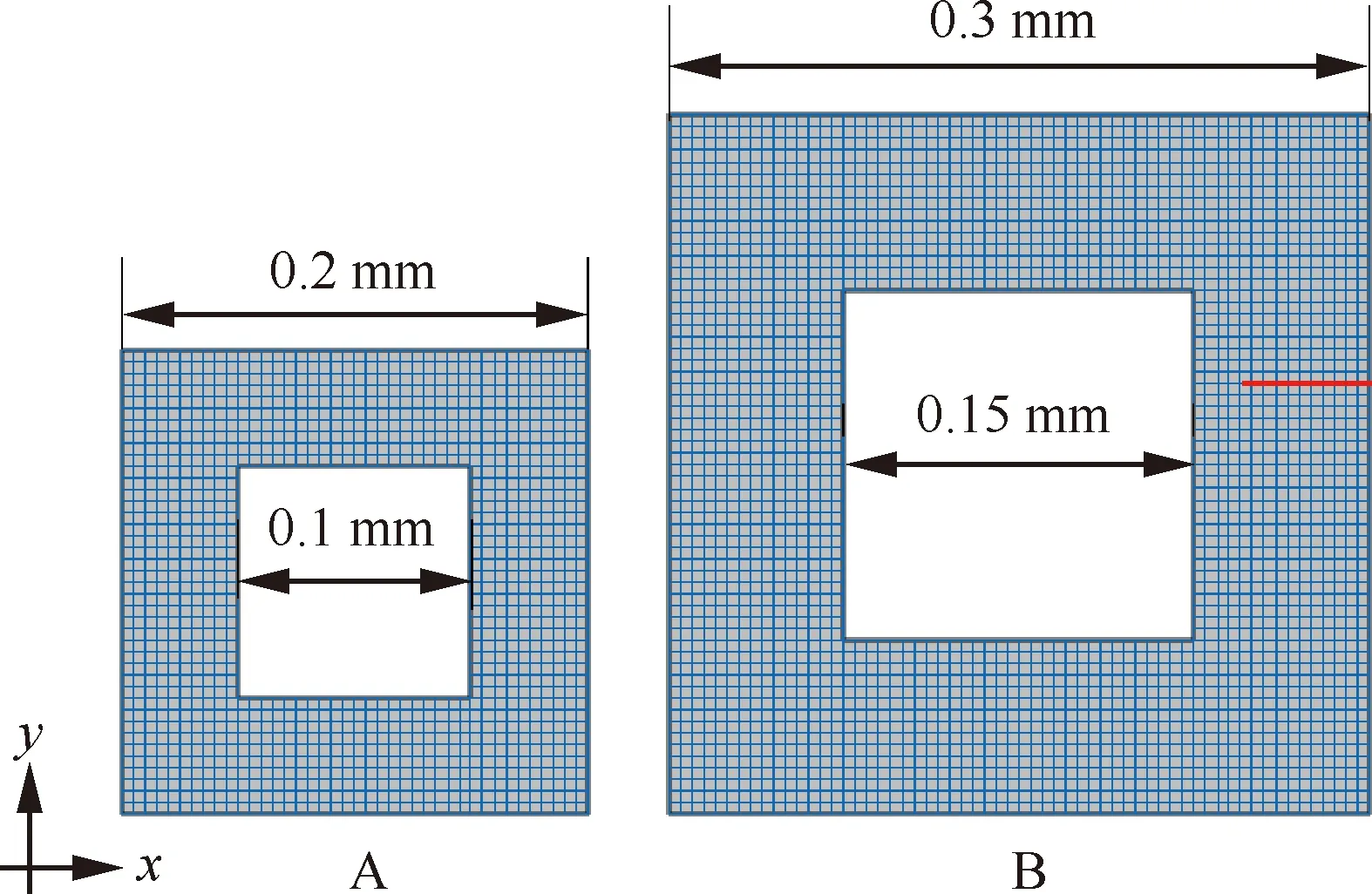
图4 2种不同尺寸单胞的几何构型和网格剖分Fig.4 Geometrical configurations and FE meshes of two cells of different sizes

选择拉伸和剪切加载过程中方孔单胞相场最大值分别为0.05、0.10、0.20时的弹性应变能作为损伤判定的阈值，并进行编号，如表1所示。对

图5 单胞A测试工况下弹性应变能-位移曲线和裂纹轨迹Fig.5 Elastic energy-displacement curves and crack paths of cell A under testing loads

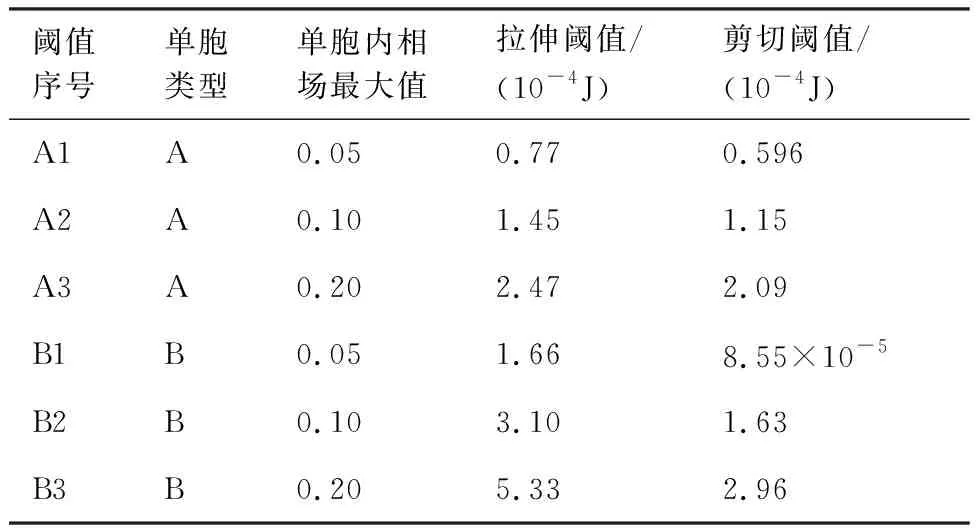
表1 单胞的损伤识别能量阈值Table 1 Energy thresholds for cell damage identification

比2种工况下标定的能量阈值，剪切加载的阈值均小于拉伸加载的阈值。后续算例验算中，选取剪切工况下标定的能量阈值作为单胞损伤的判定阈值。

3.2 Ⅱ 型断裂模拟

考虑如图6所示的II型断裂模拟算例，该结构由900个方孔单胞A周期性排列构成。该结构边长6 mm，内部预置3 mm长度裂纹，下端固定，上端施加方向位移荷载，增量为5×10mm，共加载350步。全域离散的有限元模型含节点数111.8万；采用子结构法对内部节点进行凝聚，计算节点数降低至7.4万。加载过程中，弹性应变能大于损伤识别能量阈值的子结构数目逐步增多,计算规模随之相应增大。分别采用常规相场法和本文方法进行该结构的断裂模拟，比对不同损伤阈值对模拟精度的影响。图7为采用2种相场法预测的载荷-位移曲线以及采用A2损伤阈值时的裂纹轨迹扩展情况(图6虚框区域)。图8为采用2种相场法预测的最终裂纹轨迹(图6 虚框区域)。图7、图8中红框区域为经识别需求解内部物理响应和裂纹相场的子结构。对比可见，采用A3损伤阈值时，本文方法与常规相场法的模拟结果偏差较大；而取值相对保守的A1、A2损伤阈值时，与常规相场法模拟结果的一致性较好。图9所示为3种不同损伤阈值取

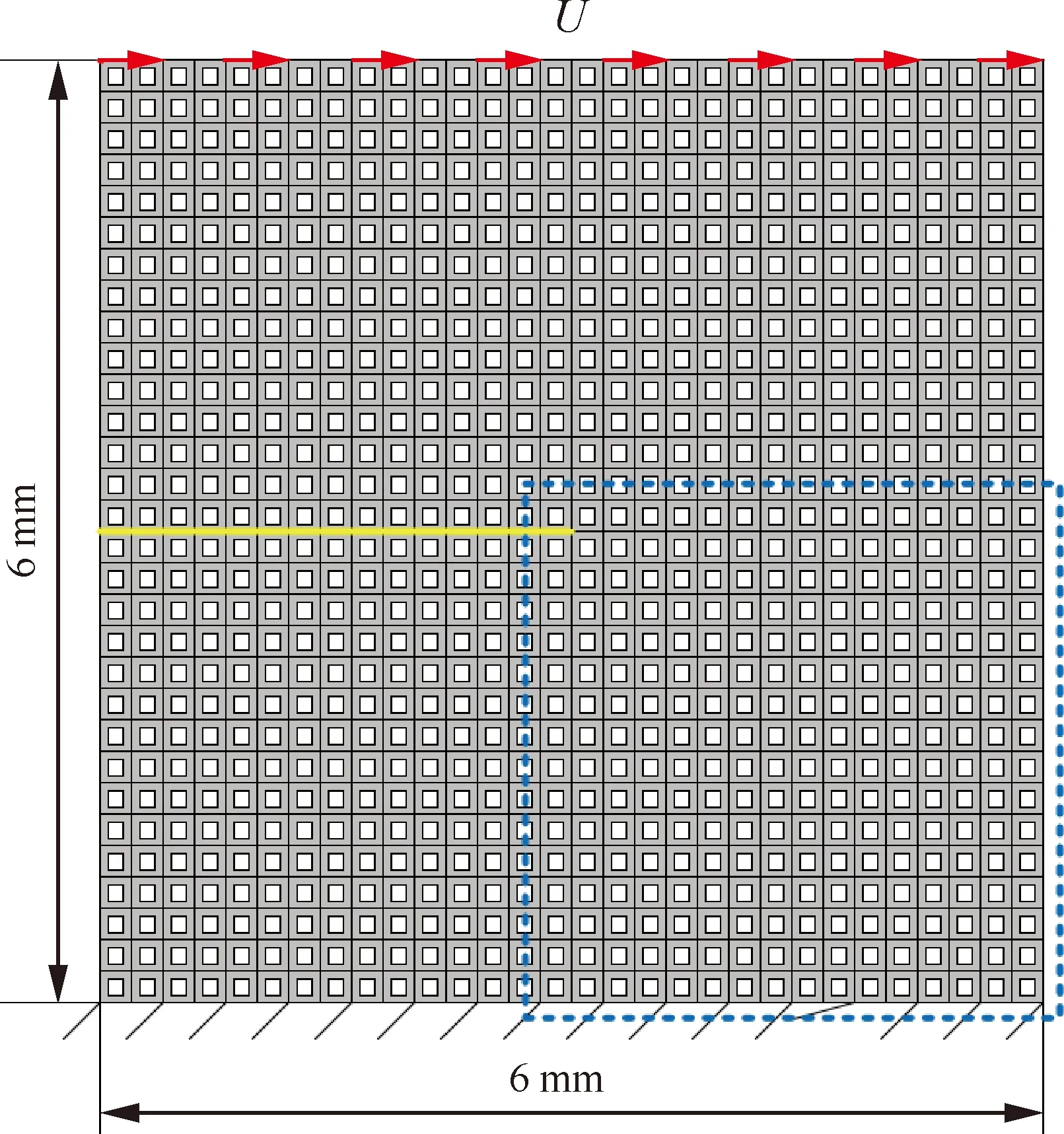
图6 周期性结构的Ⅱ型断裂问题Fig.6 Mode Ⅱ fracture of periodic structure

值情况下，加载过程中经识别需进一步求解内部响应子结构数量的占比情况。即使是最为保守的A1损伤阈值情况下，最终经识别需进一步求解的子结构数量的占比仅为16.7%(150/900)，计算规模显著降低。

图7 周期性结构Ⅱ型断裂问题的载荷-位移曲线及裂纹扩展情况Fig.7 Load-displacement curves and crack propagation of mode Ⅱ fracturing of periodic structure

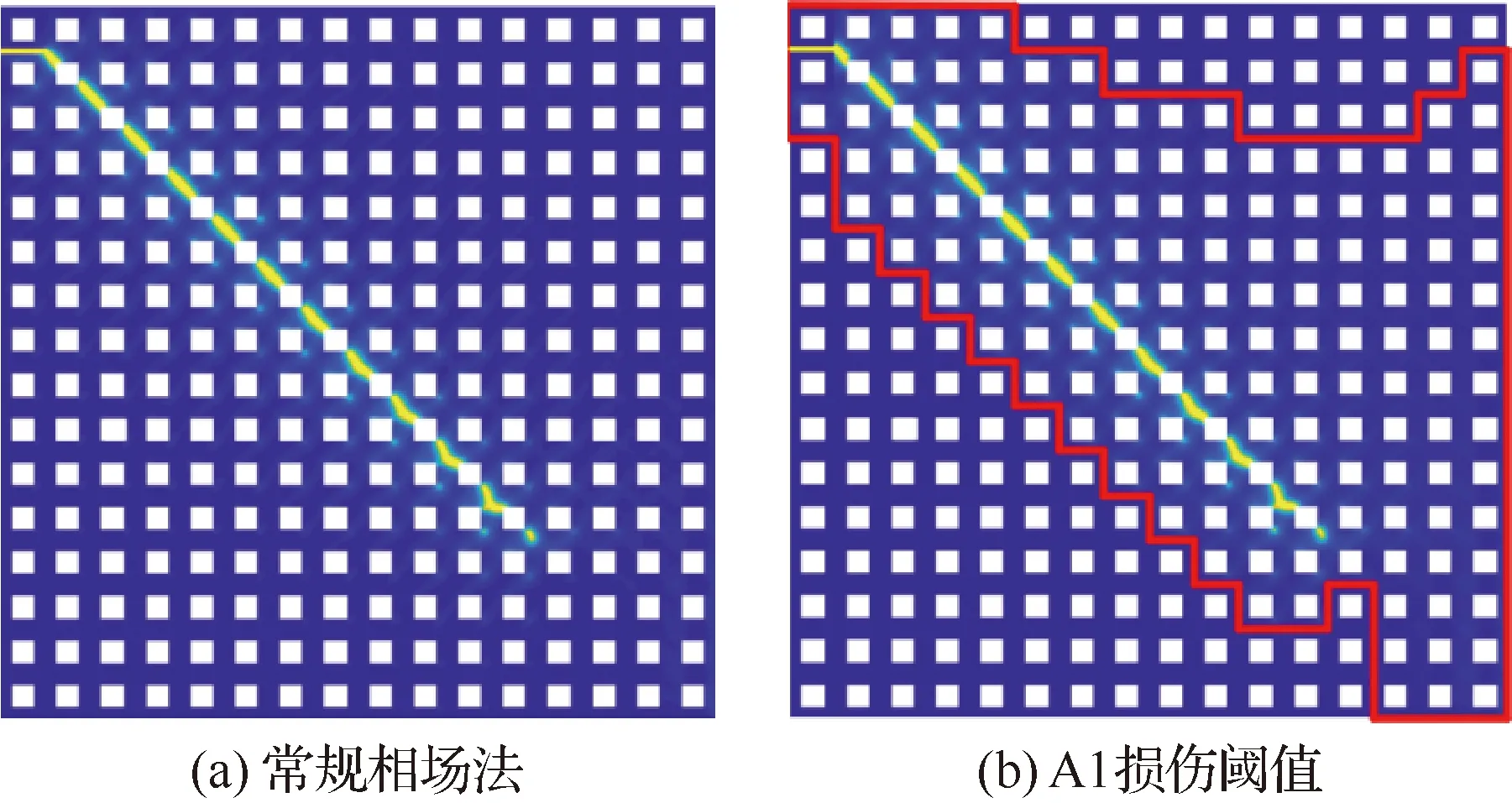
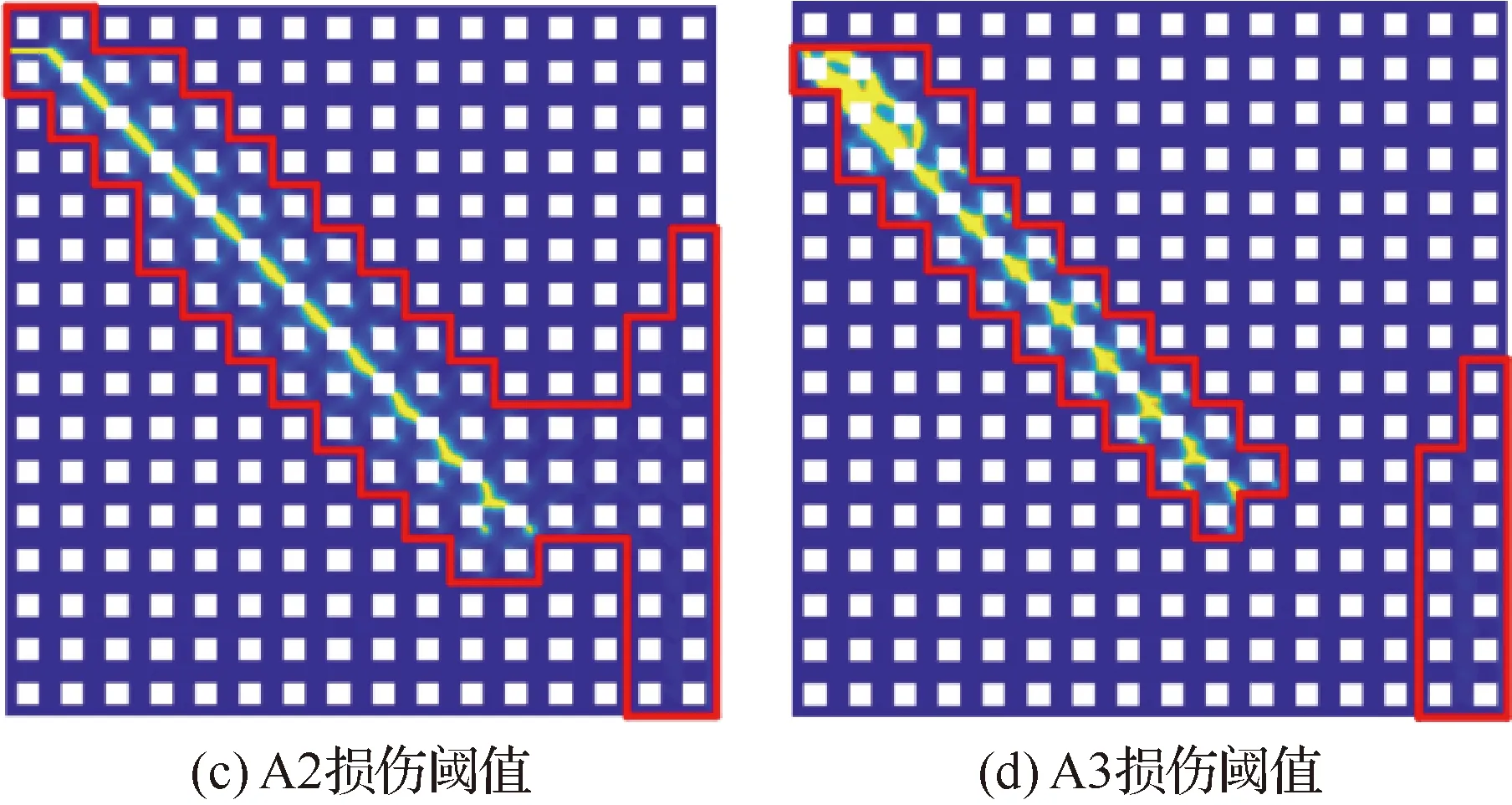
图8 周期性结构Ⅱ型断裂问题的最终裂纹轨迹Fig.8 Ultimate crack paths of mode Ⅱ fracturing of periodic structure

图9 Ⅱ型断裂问题过程中含裂纹子结构占比Fig.9 Proportion of substructures with cracks during mode Ⅱ fracturing

3.3 L形梁断裂

进一步验证本文所提方法的适用性,考虑如图10所示的由675个方孔单胞A周期性排列构成的L形梁的断裂模拟。将L形梁的下端固定，在图示箭头处竖直向上施加位移荷载，增量为1×10mm，共加载200步。根据前一算例分析结果，综合考虑模拟精度和计算规模，选择能量阈值A2进行子结构的损伤识别。分别若采用常规相场法和本文方法进行该结构的断裂模拟。图11为采用2种相场法预测的载荷-位移曲线。图12为采用2种相场法预测的最终裂纹轨迹(图10虚框区域)。2种方法模拟结果的一致性较好。图12(b)中红框区域为经识别最终需求解内部响应的子结构，仅占子结构总数的4.6%(31/675)，计算规模显著低于常规相场法。

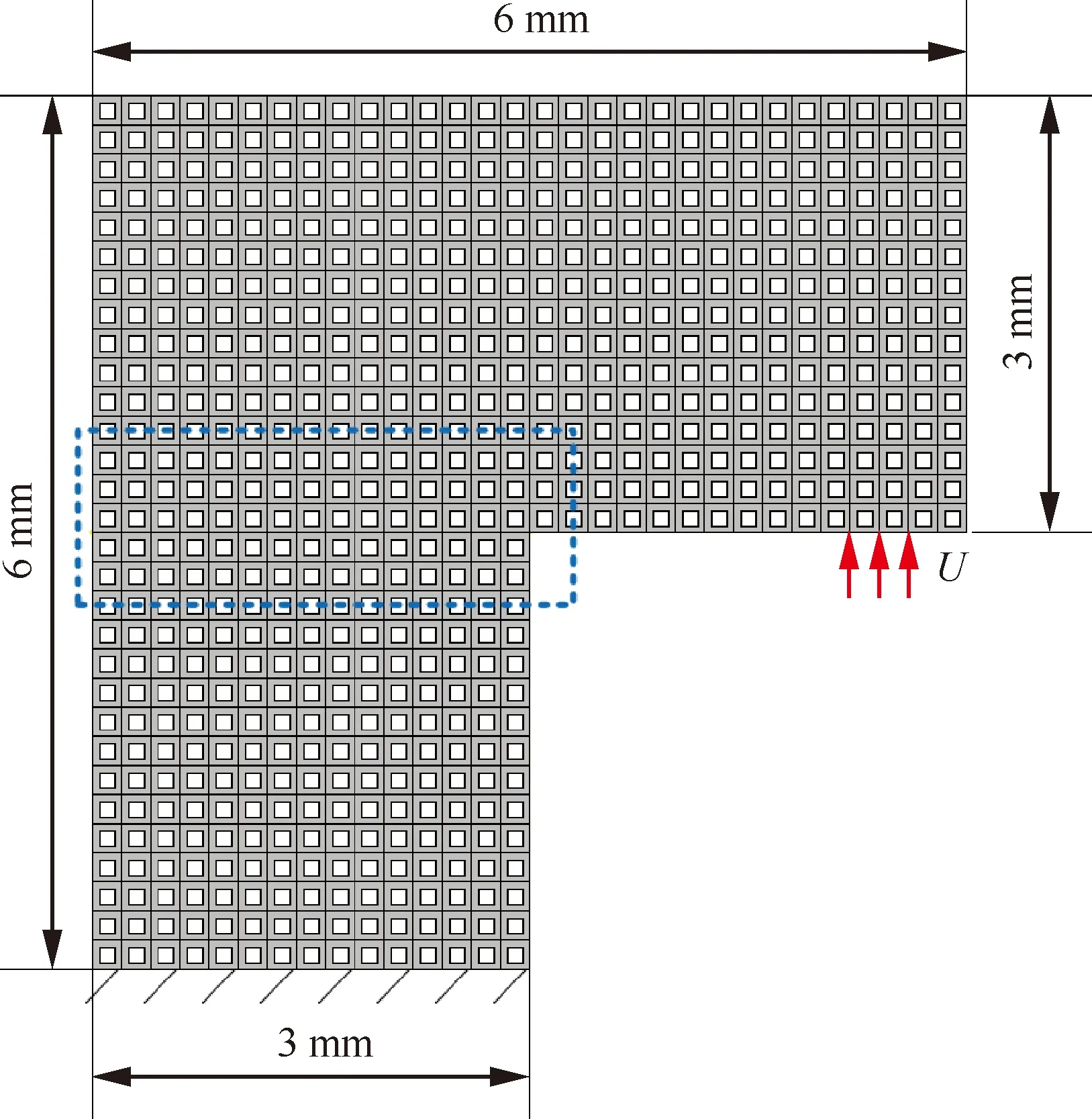
图10 单胞A周期性排列构成的L形梁Fig.10 L-beam periodically composed with cell A

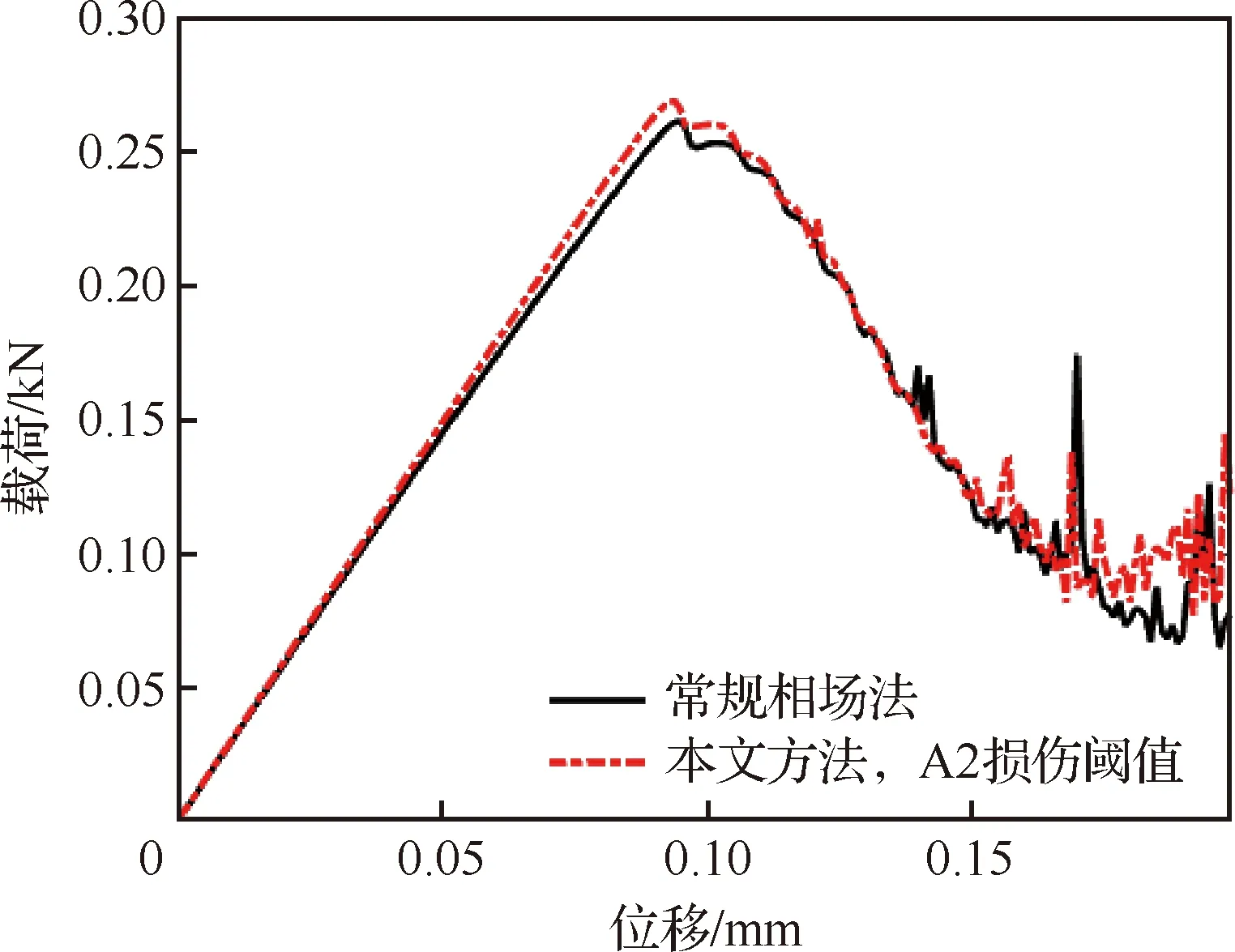
图11 单胞A组成的L形梁断裂模拟载荷-位移曲线Fig.11 Load-displacement curves of fracture modeling for L-beam composed of cell A

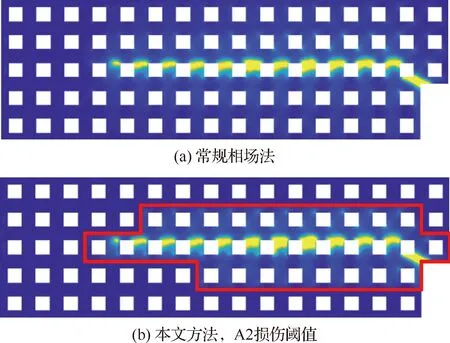
图12 单胞A组成的L形梁断裂模拟最终裂纹轨迹Fig.12 Ultimate crack paths of fracture modeling for L-beam composed of cell A

接下来，进一步验证方法的适用性，考虑由300个方孔单胞B周期性排列构成的L形梁的断裂模拟，如图13所示。类似地，选择表1中对应的能量阈值B2进行子结构的损伤识别。图14为采用2种相场法预测的载荷-位移曲线。图15为采用2种相场法预测的最终裂纹轨迹(图13虚框区域)。与前一算例类似，2种方法模拟结果的一致性较好，且计算规模得到显著降低；图15(b)中红框区域识别出的子结构数目占比为6.3%(19/300)。对比图11、图14的载荷-位移曲线及图12、图15的最终裂纹扩展形式，周期性结构的承载极限和裂纹扩展的轨迹取决于结构整体的几

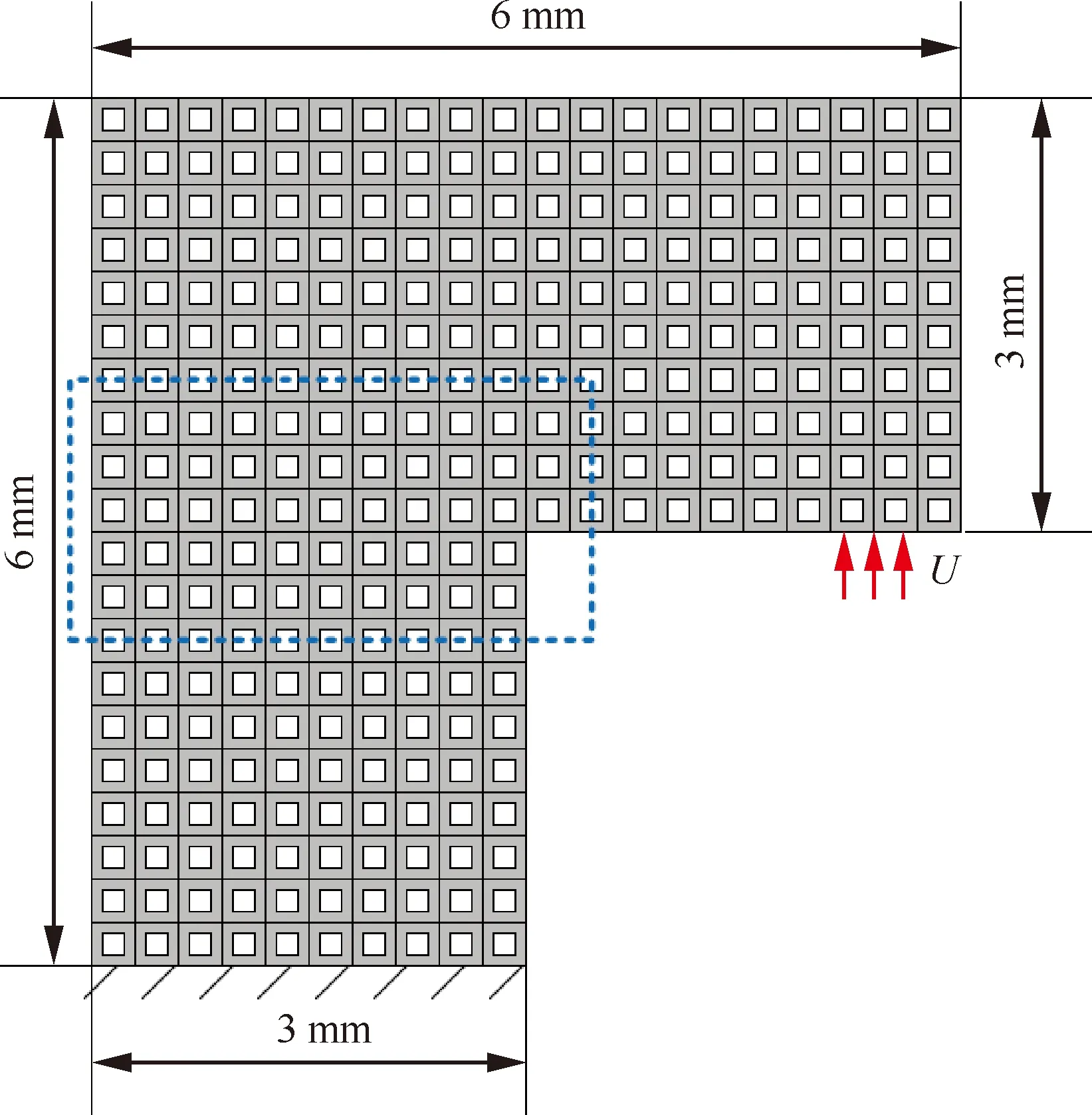
图13 单胞B周期性排列构成的L形梁Fig.13 L-beam periodically composed of cell B

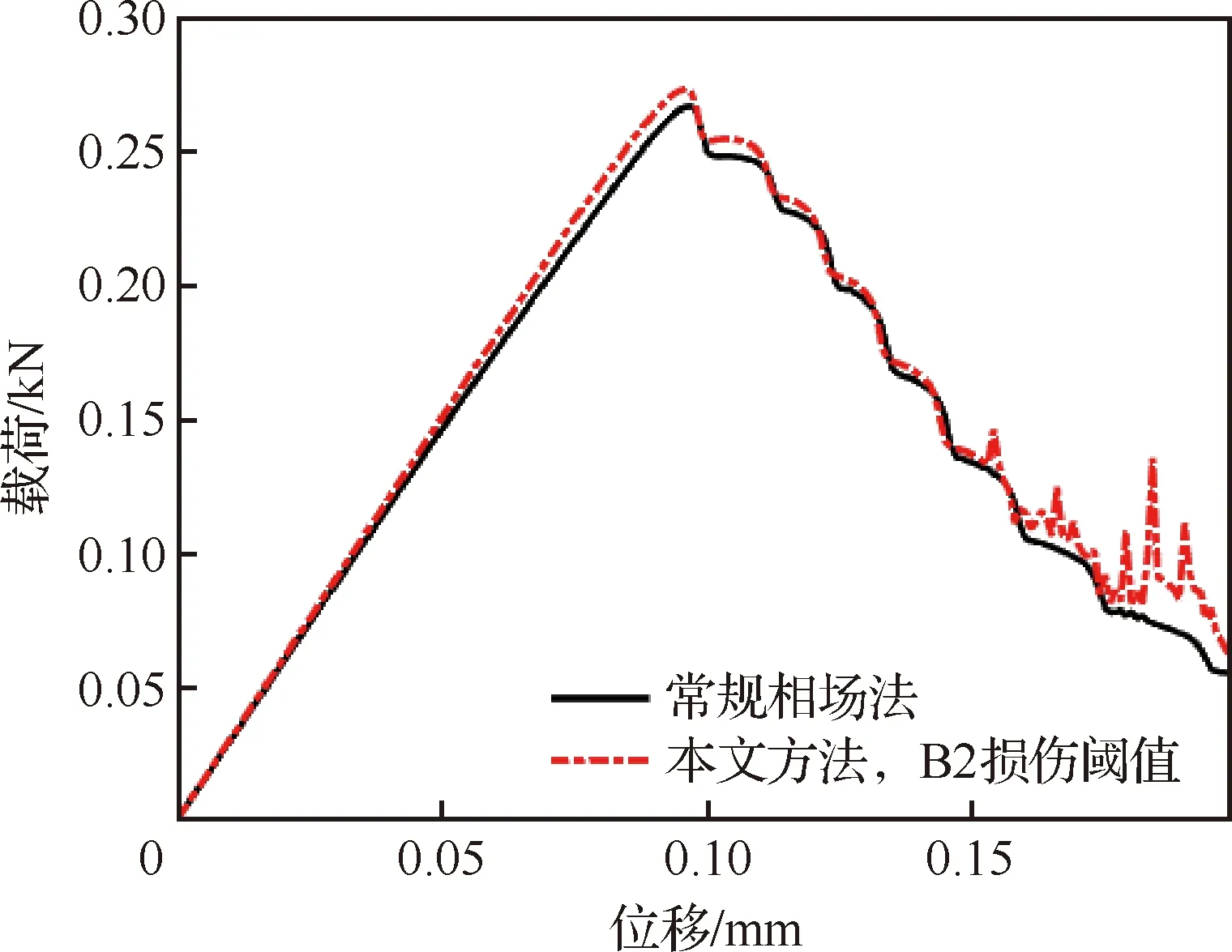
图14 单胞B组成的L形梁断裂模拟载荷-位移曲线Fig.14 Load-displacement curves of fracture modeling for L-beam composed of cell B

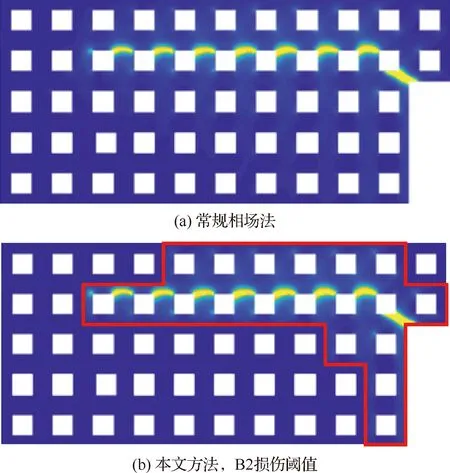
图15 单胞B组成的L形梁断裂模拟最终裂纹轨迹Fig.15 Ultimate crack paths of fracture modeling for L-beam composed of cell B

何构型和边界条件，受单胞尺寸的影响不显著。单胞尺寸较大时，裂纹间断式成核扩展，L形梁的载荷-位移曲线随着裂纹的扩展波浪式下降(图14)，一定程度上提升了结构的抗裂韧性(曲线下围面积)。

4 结 论

基于子结构建模和损伤识别，发展了一种适用于周期性结构脆性断裂的高效相场模拟方法。相较于传统相场法，本文所提方法在维持断裂模拟精度的同时，能够有效地避免非裂纹扩展区域的重复计算消耗、显著降低了有限元计算分析规模。后续研究工作中，计划基于人工神经网络对单胞的承载类型进行区分，根据承载类型标定类型相关的损伤阈值，以实现更复杂周期性结构的断裂模拟。针对三维周期性结构断裂模拟求解规模大，静态凝聚耗时长的问题，后续计划结合其他平台或其他高效算法(如基于子结构法的并行计算)以降低耗时，将本方法扩展到三维断裂问题。此外，基于发展的高效断裂分析方法，有望进一步结合优化设计，通过优化单胞的几何或拓扑构型，提升周期性结构的抗裂韧性。