基于双区域模型的钠冷快堆组件子通道分析程序的开发与验证
吴宗芸,刘天才,吴明宇
(中国原子能科学研究院,北京 102413)
由于子通道分析方法能详细地考虑反应堆组件内每个通道的质量、能量、动量守恒过程并且相对于CFD方法具有较高的计算效率,因此子通道分析方法被广泛用于钠冷快堆的设计。然而,由于钠冷快堆普遍使用绕丝对燃料棒进行定位,对钠冷快堆组件进行子通道分析时,需对绕丝带来的交混效应进行准确模拟以更准确计算冷却剂的温度场分布。在子通道分析程序中常使用的绕丝模型可分为3类:强迫横流模型、分布式阻力模型和双区域模型。在COBRA[1]系列子通道程序中,绕丝对组件内温度场以及流场带来的影响使用强迫横流模型来处理,这种模型认为绕丝在绕过燃料棒间的间隙时,会带来沿着绕丝绕向的横向流动。在MATRA-LMR[2]、SACOS-PB[3]、ATHAS-LMR[4]等子通道分析程序中,使用分布式阻力模型[4]来模拟绕丝带来的效应,这类模型通过考虑绕丝对轴向流动以及间隙横流的流动阻力来模拟绕丝对流场的影响。相对于强迫横流模型,分布式阻力模型更适用于低流量工况。但这两种模型在组件径向功率倾斜分布时,计算得到的结果与实验值相差较大[5]。第3类在子通道分析中使用的绕丝模型是双区域模型[6],这种模型被用在专门针对钠冷快堆开发的子通道分析程序ENERGY和SLTHEN中,该模型可较为详细地考虑子通道间的各种交混机理并且相对于前两种模型能较为准确预测组件非均匀功率分布下的冷却剂温度场[7]。但由于ENERGY和SLTHEN程序中使用简化后的子通道守恒方程,ENERGY和SLTHEN程序使用理论计算来得到割流系数以及内部通道和壁面通道的速度,并且程序内部的模型只有内部区域和外部区域两个速度场,每个区域有相同的流速,而在实际情况中每个通道内的流速往往是不同的。因此ENERGY和SLTHEN程序计算得到的结果与一些重要的实验数据有较大偏差[7]。
除上述程序外,针对液态金属冷却快堆子通道分析,近年来还开发了一系列其他的子通道分析程序,如KMC-Sub[8]、SUBAC[9]和COBRA-LM[10],但这几款程序使用集总的交混系数来考虑绕丝的湍流交混,模型较为粗糙;ANTEO子通道分析程序[11]中也使用了双区域模型来考虑绕丝的交混效应,其对WARD实验的验证结果在高流量工况下明显好于二次开发后的COBRA,但该程序在低雷诺数工况下与实验值有较大的偏差[11];一些其他开发的子通道分析程序的文献[12-14]中未深入介绍使用的绕丝交混模型。在这些程序公开发表的验证工作中只有极少数对功率偏斜工况进行了验证,而且国内关于双区域模型的子通道分析程序的开发研究在公开文献中还较为少见。
本文使用双区域模型来模拟绕丝带来的效应,建立相应的子通道守恒方程来考虑每个通道内的质量、能量、动量守恒,并结合液态金属钠的物性、对流换热与流动阻力模型开发专门针对钠冷快堆组件热工水力分析的子通道程序SPLICA(sub-channel program for liquid metal cooled assembly)。
1 带绕丝棒束组件的双区域模型子通道模型
在双区域模型中,整个组件被分为两个区域:由内部通道组成的内部区域以及由边通道和角通道组成的外部区域。在该模型中,绕丝在内部区域和外部区域的交混效应采用不同的方式考虑。在由内部通道组成的内部区域中,间隙两端围绕燃料棒螺旋的绕丝交替穿过间隙,导致了间隙上的间隙横流强度的一次谐波近似为正弦函数[15]。双区域模型示意图如图1所示,绕丝在内部区域周期性的间隙横流增强了通道间的扩散作用,使子通道间的温差与冷却剂流量差减小。而在由边通道和交通道的外部区域中,由于绕丝每次穿过燃料棒与组件盒之间的外围间隙时均沿着同一方向,因此带来了外围间隙的单向对流交混。对于处于堆芯外围的组件,燃料棒的功率在组件内呈现明显的倾斜非均匀分布,这时外围间隙的单向流动对组件内冷却剂的温度分布具有非常明显的影响。利用这样的基本物理模型,建立子通道分析双区域模型的基本守恒方程与本构模型。

图1 双区域模型示意图Fig.1 Schematic diagram of two-region model
1.1 子通道守恒方程
子通道控制体质量守恒方程:
(1)
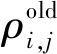
能量守恒方程:
(2)
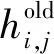
轴向动量守恒方程:
(3)
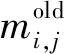
与COBRA这类子通道分析程序不同,本文开发的子通道分析程序不包含横向动量守恒方程。由于在钠冷快堆中,绕丝对间隙的横流强度与方向起着决定性的影响,因此使用横向动量守恒方程来求解得到的间隙横流往往与实验值具有较大的偏差。在本文开发的子通道分析程序中,轴向动量守恒方程采用轴向等压近似求解[15]。
1.2 绕丝棒束组件的流动压降模型
为使子通道分析程序能适用于低流量工况下的计算,流动压降模型需考虑层流区、层流-湍流过渡区、湍流区下的流动阻力。本文选择详细CT(Cheng-Todreas)模型[16]来计算绕丝棒束的流动压降,该模型覆盖了广泛的雷诺数范围,具有良好的适用性。该模型不同类型的通道流动阻力使用不同的公式表示。
内部通道的阻力系数f1:
(4)
边通道的阻力系数f2:
(5)
角通道的阻力系数f3:
(6)
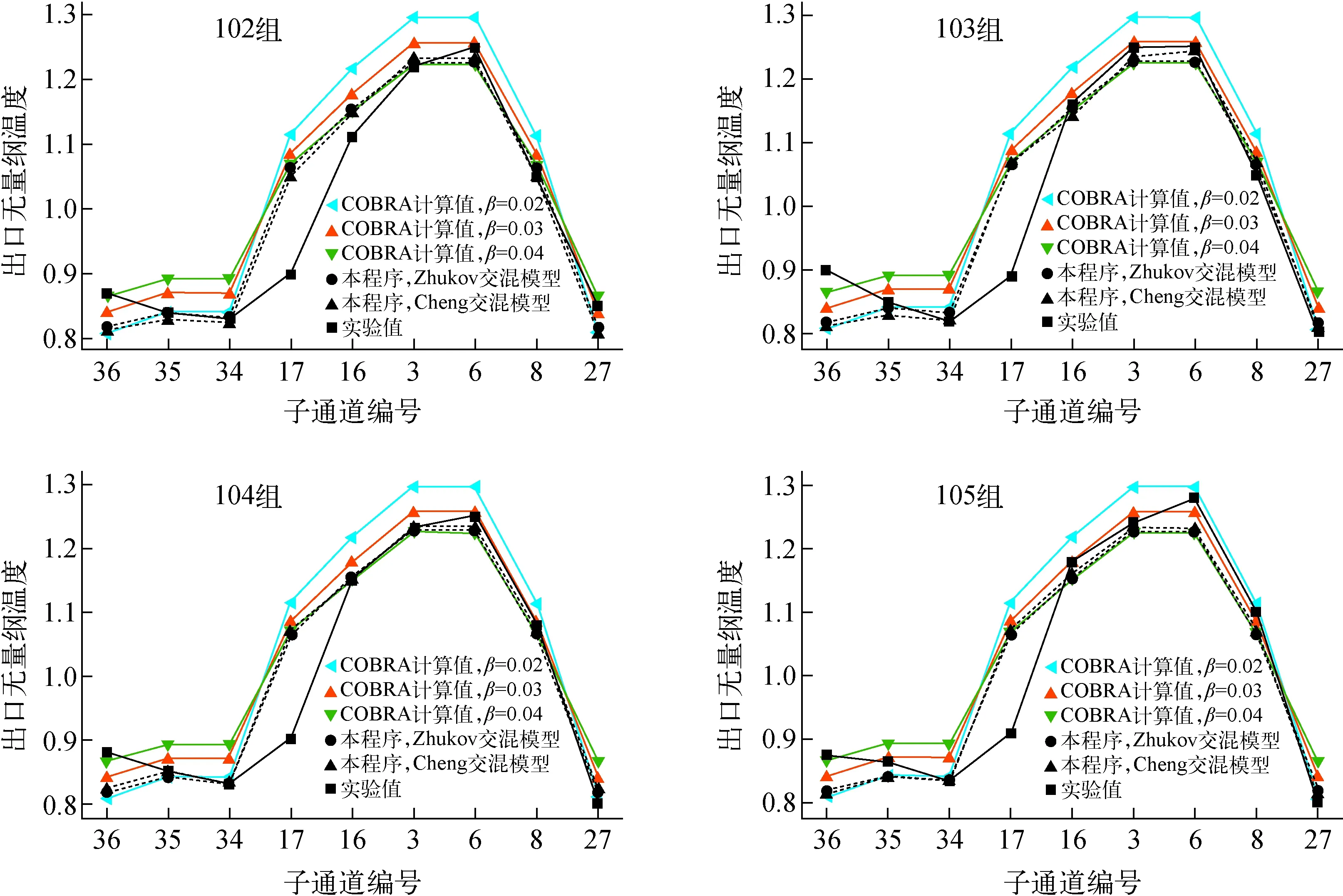
式中:m为常数,层流流动工况下m=1.0,湍流流动工况下m=0.18;θ为绕丝与轴向方向的夹角;下标i=1,2,3分别表示内部通道、边通道以及角通道。
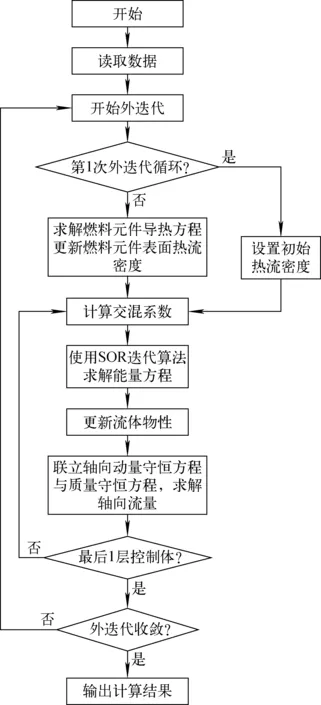
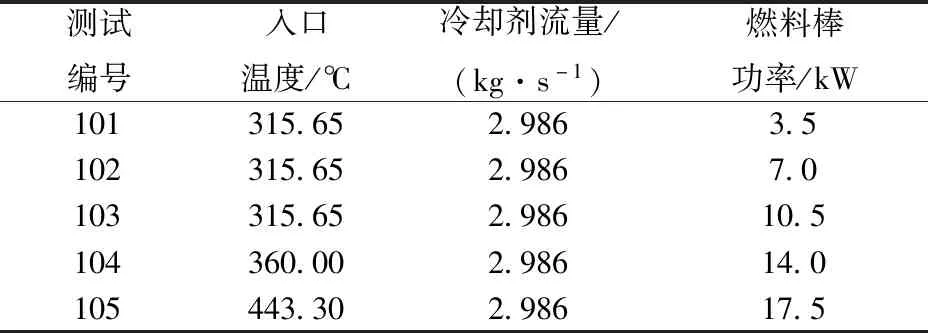
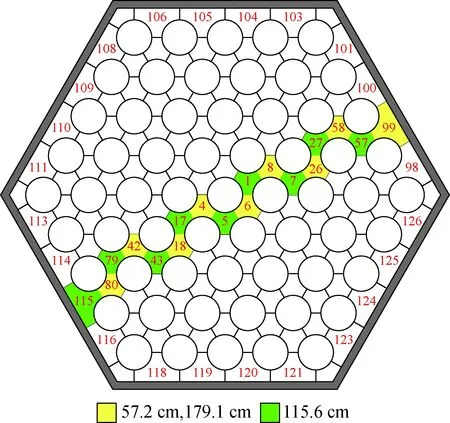
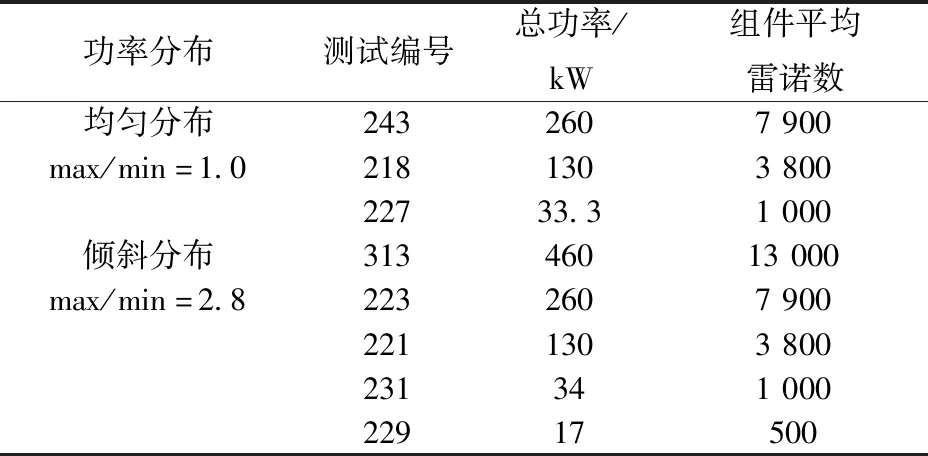
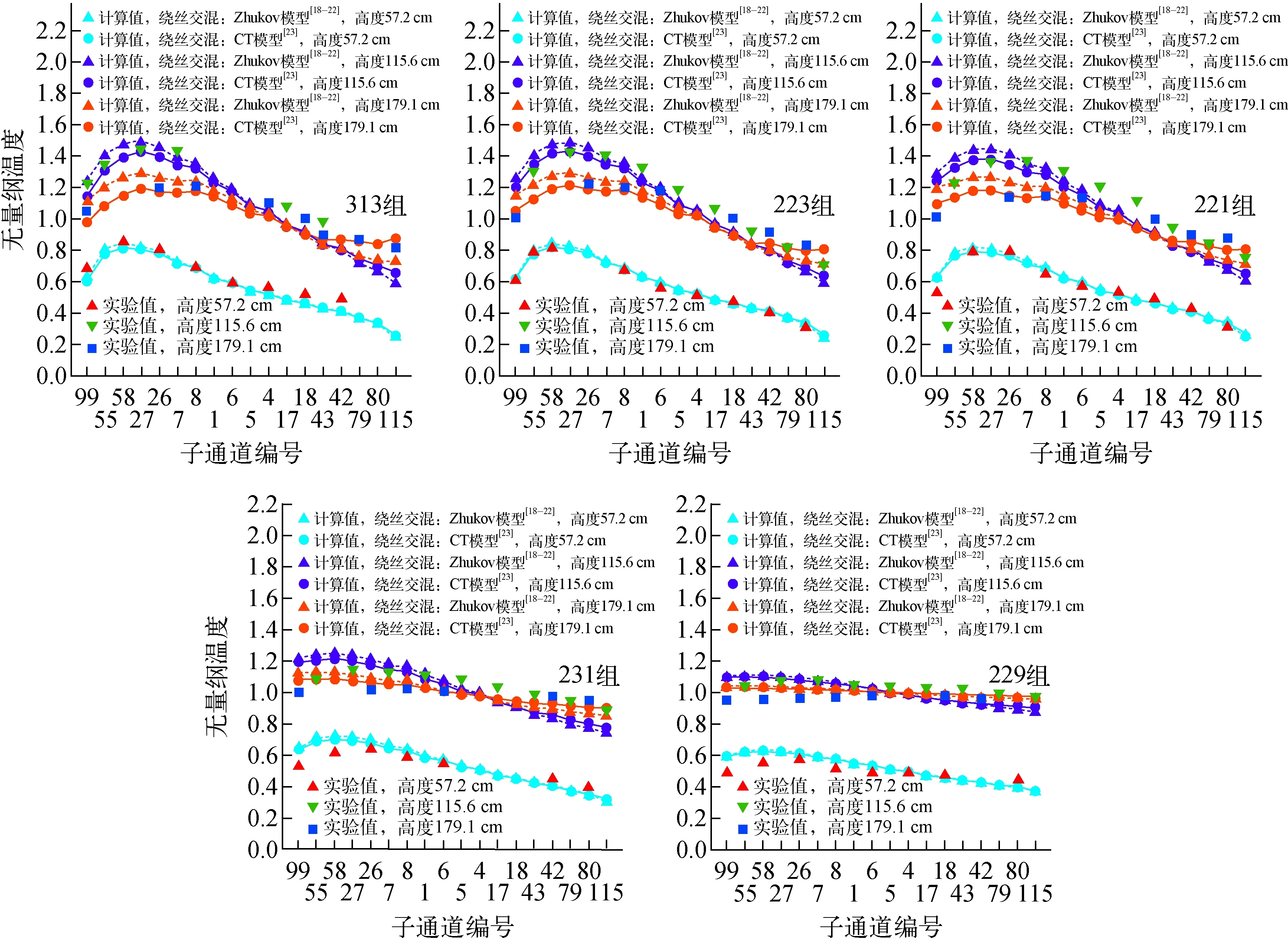
当棒束通道的平均雷诺数Reb (7) 对于层流和湍流过渡区,流动阻力系数f使用插值计算: f=fRebLψ1/3+fRebT(1-ψ)1/3 (8) 在本程序中单相对流换热系数采用Mikityuk关系式[17]。Mikityuk在2009年对以前的对流换热关系式进行了对比分析,拟合了如下的关系式: Nu=0.047(1-exp(-3.8(P/d-1)))· (Pe0.77+250) (9) 式中:S为燃料棒的间距;d为燃料棒的直径;Pe为佩特莱数。适用范围:1.1≤P/d≤1.95,30≤Pe≤5 000。 本文选用Zhukov交混模型和Cheng-Todreas交混模型来计算通道间的能量交混系数和动量交混系数。交混模型是封闭双区域子通道守恒方程组的关键,并对计算得到的结果的准确性有至关重要的影响。 1)Zhukov绕丝棒束交混模型 Zhukov交混模型使用下面的公式计算交混系数。 (10) 式(10)的适用范围为40≤Pe≤1 500,1.15≤S/d≤1.32,0.005≤Pr≤0.03,其中,Re为间隙相连两个通道的平均雷诺数,Pr为平均普朗特数。 Ψ(Re)=1-0.694exp(0.132×10-3Re) (11) (12) 式中,Δ为组件盒内壁面与最外侧燃料棒包壳之间的间隙宽度。 (13) (1-exp(-40(S/d-1))) (14) 2)Cheng-Todreas绕丝棒束交混模型 与Zhukov模型不同,Cheng-Todreas模型使用一个系数来考虑内部通道的间隙湍流与绕丝交混引起的总体扩散效应,而非将分子-湍流交混和绕丝引起的交混单独考虑。并且Cheng-Todreas模型依赖于棒束的流动是否处于湍流区,对于湍流和层流流动工况使用不同的公式计算,在层流和湍流过渡区时,Cheng-Todreas模型使用插值来计算交混系数。Cheng-Todreas模型[23]采用如下的公式来计算通道之间的交混: (15) 式中:Gin为内部通道的质量流量;θ为绕丝与轴向方向的夹角;Bij为间隙的宽度。 对于组件的外围间隙,其与1根燃料棒以及燃料组件盒壁相接,因此湍流带来的扩散效应以及绕丝带来的单向对流交混需单独考虑。 外围间隙的湍流扩散交混使用下式计算: (16) 式中,Gside为边通道的质量流量。 外围间隙的绕丝带来的单向对流交混使用下式计算: C1L=Cm1(Ar2/A′1)0.5tanθ (17) 式中,系数Cm1、Cm2依赖于棒束的流动工况以及组件棒束的几何。 对于湍流区(Reb>RebT)以及组件燃料棒数Nr≥19: Cm1T=0.14(B/D)-0.5 Cm2T=0.75(H/D)0.3 (18) 对于湍流区以及组件燃料棒数Nr≤7: Cm1T=0.1(B/D)-0.5 Cm2T=0.6(H/D)0.3 (19) 对于层流区(Reb Cm1L=0.5(B/D)0.6Cm1T Cm2L=0.5(B/D)0.6Cm2T (20) 对于层流湍流过渡区(RebL Cm1=Cm1L+(Cm1T-Cm1L)ψ2/3 Cm2=Cm2L+(Cm2T-Cm2L)ψ2/3 (21) 对于Cheng-Todreas交混模型,动量交混系数ηk,j与能量交混系数wk,j的取值一致。 本文利用面向对象的C++语言完成子通道分析程序SPLICA的开发,程序中能量守恒方程在组件的每个轴向平面上使用SOR迭代法来隐式求解,动量守恒方程与质量守恒方程联立并采用轴向等压近似方法求解。SPLICA程序可接受系统压力、入口流量或组件棒束压降、入口冷却剂温度或冷却剂比焓作为其边界条件。程序具有稳态以及缓慢变化瞬态的计算功能,并且能计算燃料元件内部的热传导。图2为本文所开发的子通道分析程序的计算流程图。程序使用逐层求解的方式,在每一层计算完成后再沿着轴向计算下一层,最后得到整个组件上的热工水力工况参数。在每次外迭代中,程序求解燃料元件的导热微分方程以更新燃料元件表面的热流密度。并从组件的入口层沿着轴向计算到出口层,对每层冷却剂控制体使用能量守恒方程求解得到冷却剂的温度,然后根据当前层冷却剂控制体的温度与压力更新当前层冷却剂控制体的物性,之后根据动量方程与质量守恒方程,求解得到当前层控制体的出口冷却剂质量流量。当整个外迭代收敛时,输出计算结果。 图2 SPLICA程序计算流程图Fig.2 Flow chart of SPLICA subchannel code FFM(fuel failure mockup)组件实验[24]是由美国橡树林国家实验室(ORNL)进行的。该实验装置专门用于研究钠冷快堆的堆芯热工水力问题。FFM是一个高温钠冷却实验装置,测试段使用19根棒束模拟液态金属冷却反应堆的堆芯组件,采用电加热棒将热量传递给冷却剂钠。该实验装置的测试段子通道划分与编号方案如图3所示。FFM实验中液态金属钠的温度最高可达650 ℃,棒束的最大线功率为33.3 kW/m,冷却剂最高流量为12.2 kg/s、最低为0.05 kg/s。整个实验段的长度为1.016 m,其中非加热入口段长305 mm,加入实验段长度为533.75 mm,非加热出口段的长度为76.25 mm。实验段组件的参数列于表1。表2列出了101~105组高流量实验的入口温度、流量以及加热棒功率条件,整个测试段运行在大气压下。 图3 FFM 2A实验组件编号方案Fig.3 Sub-channel numbering scheme for FFM 2A assembly 表1 FFM 2A 19棒束实验测试段组件参数Table 1 FFM 2A 19-rod bundle experiment test section component parameter 表2 FFM 2A 高流量实验工况参数Table 2 Parameter of FFM 2A high flow rate experimental condition 图4示出了对于FFM 2A高流量实验102~105组计算得到的无量纲温度的计算值与实验值,子通道i的无量纲温度Tnorm,i的定义为: (22) 图4 FFM 2A实验段出口无量纲温度计算值与实验值对比Fig.4 Comparison between calculated and experimental values of dimensionless temperature at exit of FFM 2A experiment section WARD(westinghouse advanced reactors division)实验段的测试组件拥有61根加热棒[25]。WARD实验测试段棒束总长度为265 cm,其中加热段的长度为114.3 cm。冷却剂钠从底端入口流入,经过加热段受热后从顶端流出。在加热段的底端有一个长24.1 cm的非加热入口段。加热段的轴向功率分布为截断的余弦分布,加热段轴向线功率最大值与平均值的比值为1.40。实验测量了径向上均匀的功率分布以及倾斜的功率分布下,加热段以及加热段下游的非加热区共5个截面上的通道温度。由于WARD实验测量了大量的层流工况以及层流-湍流过渡工况下的实验数据,因此WARD实验可用来校验子通道程序在低流量工况下的温度分布计算结果。图5示出了WARD 61棒束实验的子通道划分与编号。在计算时,选取测量距离加热段底端57.2、115.6、179.1 cm的测量数据和计算数据进行比较。其中距加热段底端57.2 cm的测量截面位于加热段的中间,距加热段底端115.6 cm的测量截面处于加热段的出口位置,而距加热段底端179.1 cm的测量截面处于加热段下游的非加热区。WARD 61棒束实验的具体几何参数列于表3。图6示出了WARD倾斜功率分布实验中加热棒的功率在径向上的功率分布。 图5 WARD实验段组件子通道编号方案Fig.5 Sub-channel numbering scheme for WARD 61-rod bundle 表3 WARD 61棒束实验组件几何参数Table 3 Geometric parameter of WARD 61-rod bundle experimental assembly 图6 WARD实验组件加热棒功率倾斜径向分布 Fig.6 Inclined radial power distribution of heating rod of WARD experimental assembly 图7示出了在径向均匀功率分布下第243、218、227组实验不同轴向高度测量得到的无量纲温度分布的计算结果与实验值。对于这3组实验,其功率与冷却剂的流量大致呈正比,出口与入口的平均温差约维持在100 ℃。表4示出了这3组实验的具体工况参数。在使用子通道分析方法来计算这3个工况时,湍流交混关系式选择Zhukov模型。由于这3组实验的雷诺数范围位于层流区与层流湍流过渡区,因此在阻力模型上选择了Ki(Kirikkov)模型[26]与CT(Cheng-Todreas)[16]模型,这两种模型均考虑了层流区的摩擦阻力系数以及层流湍流过渡区的插值。从图7可看出,本文开发的子通道分析程序的计算结果与这几组实验得出的结果符合得较好,并且选择不同阻力模型带来的不确定性较小。当冷却剂质量流量减小时,不同的通道在横向上得到的温度会变得更加平滑。对于高流量时得到的温度分布会有一个比较明显的“拱形”形状。这是由于边通道的质量流量高,因此边通道的温度相对较低。而通道间通过绕丝的交混以及分子-湍流扩散传递能量,最终得到拱形的温度分布。对于轴向高度为179.1 cm的测量截面,由于其位于非加热区中,因此在非加热区中通道间的能量传递过程使得通道间的温差逐渐降低,其温度分布相对于加热段出口115.6 cm处的温度分布更加平坦。对于低流量工况,通道间的能量交换过程主要依靠通道间的导热过程。从实验227组的数据中可看出,在低流量工况下,179.1 cm处测量截面上的温度分布几乎是均匀的,在非加热区中通道间的分子-湍流热传导效应很快将温度展平。 图7 WARD均匀功率分布实验上、中、下测点的无量纲温度分布计算值与实验值对比Fig.7 Comparison between calculated and experimental values of dimensionless temperature distribution of upper,middle and lower measurement points in WARD uniform power distribution experiment 表4 WARD 61棒束实验工况参数Table 4 WARD 61-rod bundle experiment operating condition parameter 图8 WARD倾斜功率分布实验上、中、下测点的无量纲温度分布计算值与实验值对比Fig.8 Comparison between calculated and experimental values of dimensionless temperature distribution of upper,middle and lower measurement points in WARD gradient power distribution experiment 图8中同时示出了使用Cheng-Todreas绕丝棒束交混模型与使用Zhukov交混模型计算得到的各组实验的对比。从图中可看出,相比于Zhukov交混模型,Cheng-Todreas交混模型在层流湍流过渡区223、221组实验得到的结果与实验值符合得更好。并且,在高功率分布一侧的通道温度相比Zhukov交混模型计算得到的值更低。由于冷却剂在外围间隙中的单向流动,较热一侧的边通道的冷却剂流向功率较低的一侧,而较冷一侧的边通道的冷却剂流向功率较高的一侧。因此模型给出的外围间隙单向流动强度越强,高功率分布一侧的边通道的温度越低,而低功率分布的一侧的边通道温度越高。由于Cheng-Todreas模型给出的绕丝带来的外围间隙的单向对流交混强度要高于Zhukov模型,因此Cheng-Todreas模型计算得到的高功率侧的边通道99温度更低。在层流湍流过渡区,Cheng-Todreas模型给出的通道间的交混似乎相比Zhukov能与实验符合得更好。但对于高流量工况313组,Cheng-Todreas模型预测得到的外围间隙的单向横流强度相比于真实值稍高,以至于高功率侧的边通道99计算得到温度与实验值相比更低且低功率侧的边通道115得到的温度相比实验值更高。对于加热段中间的测量截面(图中的蓝线),这两种模型给出的温度差别并不明显。这是由于在距入口较近的轴向高度较低的位置,高低功率侧的边通道温度相差并不太明显,因此外围间隙的强迫横流强度对温度分布影响不大。对于低流量实验229组,由于其温度分布主要受通道简单的热传导系数影响,因此两种模型计算得到的温度分布相差并不大。在总体上来说,Cheng-Todreas给出的温度分布相比Zhukov模型与实验值符合得更好。 本文利用双区域模型开发了一款用于钠冷快堆组件热工水力分析的子通道分析程序SPLICA,SPLICA程序中通过双区域模型本构关系式详细地考虑了绕丝带来的通道间的交混效应。通过与FFM-2A 19棒束实验以及WARD 61棒束实验温度分布数据进行对比,验证了本文开发的子通道程序在层流、湍流以及层流湍流过渡区工况下对钠冷快堆组件热工水力分析具有良好的适用性,并且在组件径向功率倾斜情况下计算结果也具有较高的准确度。对于FFM 2A实验,与经过二次开发的COBRA-Ⅳ程序相比,本文开发的子通道分析程序与实验值符合得更好。对于WARD 61棒束倾斜功率分布实验,Cheng-Todreas交混模型在层流湍流过渡区计算得到的温度分布较Zhukov交混模型与实验符合得更好。本程序能为池式钠冷快堆组件的热工水力研究提供有效的设计和分析工具。1.3 单相对流换热模型
1.4 绕丝棒束通道间的交混模型
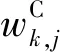

2 基于双区域模型的子通道分析程序的开发
3 算例验证与测试
3.1 ORNL-FFM 19棒束实验数据验证


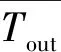
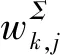
3.2 WARD 61棒束实验数据数据验证



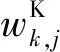
4 结论

