薄壁内镶贴片式滴灌带有限元水力计算方法及设计

魏涛，王剑，袁寿其

(江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013)

滴灌系统水力设计的主要任务是在满足灌水均匀性和平均灌水器流量的要求下，设计出投资和运行费用最低的管网系统.其中，准确的水力计算是系统设计的基础.对于支管和毛管等多孔管，其水力学解析主要是计算水头损失、孔口压力及流量，并以此评价管网设计的优劣.

近10年，内镶贴片式滴灌带由于其低压运行、易于安装和低成本投资被广泛应用于灌溉大田作物和高价值经济作物.不同于常用的插入式滴灌管和内镶圆柱式滴灌管，内镶贴片式滴灌带壁厚较薄，滴灌带过水断面随着工作压力的变化而发生改变，且贴片式滴头具有特殊结构，因此，其水流能量损失及灌水均匀度变化会体现出独特的规律.同时，当前降低能耗的背景下，低压滴灌甚至无压地下滴灌技术纷纷被提出[1]，如张林[2]采用小流量微压滴灌技术降低了滴灌系统的工作压力，最低可达到5 m.CAI等[3]利用微孔陶瓷渗灌技术进一步降低滴灌系统压力至2 m以下.因此，研究不同压力下滴灌带的水力性能至关重要.

目前，滴灌系统水力计算方法主要有解析法和数值法.如最早CHRISTIANSEN[4]应用于计算沿程水头损失的多孔系数.而后，WU等[5]提出了能量廓线法，众多学者以能量廓线的理论和公式为基础，发展出了不同坡度条件下的毛管设计方法[6].张林等[7]通过对滴灌系统综合流量偏差率的推导来指导滴灌毛管或灌水单元的设计.解析法简单易用，但多针对单条毛管.数值法通过迭代求解非线性方程或方程组对管网进行水力解析，如早期的进步法和退步法， PINTHONG等[8]利用Mapwindow插件基于最小路径法和黄金分割法对有压滴灌系统提出了一种水力计算迭代算法.随着计算机运算能力的提高，BRALTS等[9]基于有限元法提出了求解支管单元节点压力水头的方法，但由于计算机内存限制，对大型管网难以计算.康跃虎[10]基于黄金分割法简化了有限元模型，提出了满足平均灌水器流量和灌水均匀度的水力设计方法.

现有的水力计算模型中，对于将滴头引起的局部水头损失考虑到水力计算中的研究鲜有报道.由于滴头的插入，管道的局部过水断面会发生改变，流体产生紊动，进而产生局部水头损失.由于滴头数量的巨大，该部分损失不可忽略.同时计算机内存能力的提高和运算速度的加快为有限元法在滴灌系统中的应用提供了便利.为此，文中基于有限元方法，将局部水头损失添加到水力计算中，编写计算机程序并应用到不同滴灌带灌水均匀度的计算，分析了滴灌带的壁厚、滴头间距对总水头损失、滴灌带极限铺设长度、灌水均匀度的影响，以期为完善滴灌工程设计提供支持.

1 方 法

有限元法在滴灌水力解析中的应用类似于结构分析问题，文中首先介绍滴灌系统中沿程和局部水头损失的计算方法；其次针对每个单元，将能量方程转化为线性形式，根据连续性方程推导出单元刚度矩阵，应用直接刚度法得到总刚度矩阵；最后利用高斯消去法求解系统方程组，得到系统压力水头分布.

1.1 系统水头损失计算

图1为滴灌带任一管段(单元e)，图中节点s和t为滴头；Zs，Zt分别为节点s,t处的位置水头；Hs,Ht分别为节点s,t处的压强水头；hf为沿程水头损失；hj为局部水头损失；vs，vt分别为s,t处的流速.

沿程水头损失通过Darcy-Weisbach公式结合Blasius公式计算，即

(1)

式中：L为滴头间距，m；D为管道内径，m；Q为管道内流量，m3/s；ν为流体黏度，m2/s.

PROVENZANO等[11]认为滴灌带的过水断面具有特殊几何结构，其Blasius公式中的常数c应为更小的值，c=0.285.因此，将式(1)改进为

(2)

由于薄壁滴灌带受压力影响，内部形成非规则圆形的过水断面，当压力较低时，其断面可近似为2段圆弧组成的近椭圆形，如图2所示.式(2)中的管径需要替换为一种当量直径[11-12]，为过水断面水力半径的4倍，即

(3)

式中：A为断面的面积，m2；P为断面的周长，m；Rh为水力半径；ω为圆弧的中心角；r为圆弧半径，m.

ω和r的计算方法分别如图2所示，图中x为断面横径的1/2，m；y为断面纵径的1/2，m.

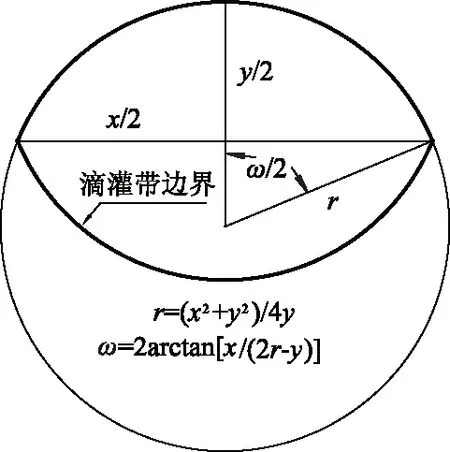
图2 滴灌带边界及过水断面示意图

不同壁厚滴灌带横径和纵径随内部水压变化的规律不同，其与压力水头的关系可参考文献[12].

与插入式滴头和内镶圆柱式滴头不同，内镶贴片式滴头可近似为具有长宽高的立方体，滴头处引起的局部水头损失可通过下式计算[12]

(4)

式中：La为滴头长度，m；Lb为滴头宽度，m；Lc为滴头高度，m;v为管道内流速，m/s.

根据能量守恒定律可得

(5)

式中：ps，pt分别为节点s和t处的压强，Pa；γ为水容重，N/m3.

滴灌带内流速水头较小，可以忽略.将式(2)和(4)整合到式(5)中，得到式(6)为

Zs+Hs=Zt+Ht+kQ1.75+keQ1.218,

(6)

式(6)可改写为

(Zs+Hs)-(Zt+Ht)=(kQ0.75+keQ0.218)Q,

(7)

对式(7)进行线性化处理可得

Q=Cp(Zs+Hs)-Cp(Zt+Ht),

(8)

式中：Cp为管段总水头损失系数.

(9)

1.2 系统方程组的建立

对于图1中的管段(e)，假设节点处无出流，根据流量连续性原理，流入节点s的流量Qs为正值，流出节点t的流量Qt为负值，则式(8)可分别改写为

(10)

(11)

结合式(10)和(11)得到

(12)

式(12)为针对管道单元(e)的标准有限元形式，即

{R(e)}=[k(e)]{H(e)}-{f(e)},

(13)

式中：{R(e)}为残差向量；[k(e)]为单元刚度矩阵；{H(e)}为待求节点压力水头向量；{f(e)}为地形影响的单元作用力向量.

通过直接刚度法[13]，根据单元两端节点编号，将单元刚度矩阵扩展为贡献矩阵，再迭加到结构总刚度矩阵中对应的位置上去，得到系统方程组为

KH-F=0,

(14)

式中：K为总刚度矩阵；H为未知节点水头向量；F为系统作用力向量.

假设节点s处有滴头，其压力流量关系可表示为

(15)

式中：q为滴头流量，L/h；k和x分别为滴头流量系数和指数.

针对节点s，根据质量守恒定律有

(16)

此时，式(12)中单元刚度矩阵修改为

(17)

当节点处有滴头时，根据节点编号，系数Ce被添加到总刚度矩阵中对应的位置中.

1.3 系统方程组的求解

通过有限元法迭代求解系统方程组式(14)得到管道压力水头分布，具体过程如下：首先确定滴灌带物理参数与节点编号，然后假设一组管道各单元内部流量，通过参数与假定流量初始值计算式(8)中各管段单元总水头损失系数Cp，进而得到式(12)中各单元刚度矩阵.根据单元节点编号建立总刚度矩阵及系统方程组(14)，求解得到各滴头压力水头，通过求解压力水头应用式(15)计算各滴头流量，进而重新计算Cp，重复求解系统方程组，直到2次求解值的偏差小于设定值，计算收敛，得到最终解.

以一条毛管为例，图3为算例滴灌带及压力水头线.

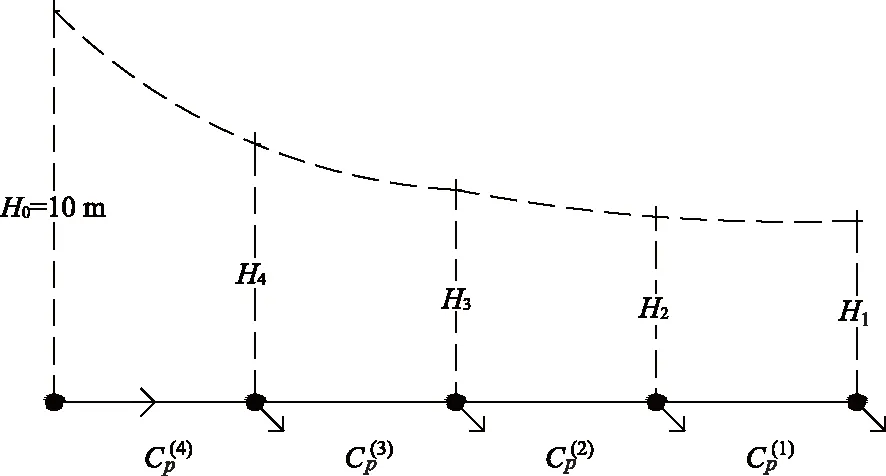
图3 算例滴灌带及压力水头线

为了方便展示系统方程组与求解各滴头压力水头的差异性，假设滴头个数为4个，末端滴头编号为1，滴头间距为100 m，额定流量为200 L/h，流态指数为0.5，入口压力为10 m，壁厚为0.46 mm，滴头长度为30 mm，滴头宽度为5 mm，滴头高度为2 mm，总刚度矩阵和系统方程组如式(18)，各管段初始流量可按入口到末端逐渐降低的方法给定.最终求解各滴头压力水头H1―H4的值分别为4.37，4.62，5.48和7.36 m，需4次迭代收敛.

(18)

2 结果与分析

2.1 入口压力对总水头损失的影响

通过以上的有限元水力解析方法，在已知滴灌带物理参数的条件下，可求解压力水头和流量分布、总水头损失和均匀度等水力参数.以一条毛管为例，相关参数：滴头间距选为0.2，0.4，0.8 m，管长100 m，滴头长度为19.38 mm，滴头宽度为5 mm，滴头高度为5.34 mm.坡度为0，滴头额定流量1.3 L/h，压力流量关系为q=0.41H0.5，壁厚d=0.38 mm.

计算结果与《微灌工程技术规范》(GB/T 50485—2009)进行对比，现有规范在灌水管网设计中并未区分毛管类型，因此采用传统Blasius公式计算沿程水头损失hf为

(19)

《微灌工程技术规范》中指出，管道局部水头损失占沿程水头损失的10%～20%.故取其最大占比20%作为管道局部水头损失值.管道总水头损失hw为沿程水头损失hf与局部水头损失hj的总和.

式(19)中管径采用厂家提供的公称直径16 mm，管道总水头损失需乘以多口系数F

(20)

式中：N为管道上出水口数目；m为流量指数，层流；m=1.00，光滑紊流层流；m=1.75，完全紊流；x为进口端至第1个出水口的距离与孔口间距之比.

图4为毛管在不同滴头间距下，总水头损失的计算值与中国《微灌工程技术规范》给出的规范值对比图,图中hw为毛管总损失，H0为毛管入口压力.

图4 总水头损失对比

不同滴头间距下，毛管总水头损失hw随毛管入口压力H0的增大而增大，且随着滴头间距的增大，相同管长条件下滴头个数减少，总出流量减少，引起相同压力下的总水头损失也减小.当滴头间距为0.4 m和0.8 m时，《微灌工程技术规范》给出的规范值比模型计算值小，其中，当压力为1 m、滴头间距为0.4 m时，有限元模型总水头损失计算值为0.28 m，而规范值仅为0.09 m.且随着压力的增大，规范值与计算值之间的差值也逐渐增大；当压力为10 m时，有限元模型的总水头损失计算值达到了1.36 m，而规范值仅为0.70 m，两者差值达到了0.66 m.但当滴头间距为0.2 m时，规范值比计算值要大，说明当滴头间距较小时，《微灌工程技术规范》给出的规范值偏大，较为安全.

2.2 壁厚对均匀度的影响

选取壁厚为0.13，0.20，0.31，0.38，0.46，0.61 mm的6根不同壁厚的毛管，管长160 m，滴头间距为0.4 m，其他参数与2.1节相同，如图5所示.由此获得压力越高，毛管的当量直径越大，均匀度也越高，其中在10 m的压力下，毛管的均匀度均在0.90以上.且随壁厚的增加而缓慢减小，但总体变化不大，而当水压在1 m时，随着毛管壁厚的增加，毛管的均匀度从0.81降至0.63，尤其是当壁厚超过0.3 mm后，均匀度开始急剧减小，其主要是由于当壁厚达到0.3 mm后，毛管的当量直径变化较大导致，其中在1 m的压力下，壁厚为0.13 mm时毛管当量直径为15.82 mm，壁厚为0.3 mm时，毛管的当量直径为15.50 mm，而当壁厚为0.6 mm时，其毛管的当量直径仅为11.66 mm.

图5 均匀度和当量直径与管道壁厚的关系

2.3 毛管极限管长设计

表1 毛管极限管长设计

所用参数与2.2算例相同，表1为基于有限元模型对不同压力和不同壁厚下的毛管极限铺设长度Lmax进行计算，即通过重复的有限元算法选择出极限铺设长度Lmax，以达到最低的设计标准(Cu=0.90)，其中，所计算毛管的滴头间距均为0.4 m.毛管极限铺设长度均随着压力的增大而逐渐延长，而当压力一定时，毛管极限铺设长度随壁厚的增加而缓慢减小，主要原因是由于壁厚的增大导致毛管的当量直径减小，进而导致总水头损失增大.但总体来看，相对于压力的影响，毛管壁厚对毛管极限铺设长度影响较小.文中使用的滴头额定流量较小，为1.3L，因此，壁厚对极限管长影响较小.对于4L以上的滴头，管道内部流量相对较大，水头损失及均匀度的变化对当量管径的变化会更加敏感，因此，极限管长的设计结果差异性会更显著.

3 结 论

1) 本研究基于有限元法，在考虑毛管壁厚及内镶贴片式滴灌带滴头结构影响的情况下，得到求解压力水头、总水头损失和均匀度等水力参数的方法，以此计算滴灌系统的灌溉均匀度并评价管网设计的优劣.

2) 以一条毛管为例，应用模型分析可知，由于毛管总水头损失hw随压力的增大而增大，且随着滴头间距的增大，相同管长条件下滴头个数减少，总出流量减少，引起相同压力下的总水头损失也减少.与《微灌工程技术规范》中总水头损失hw的推荐方法的计算结果进行对比，发现当滴头间距为0.4和0.8 m时，规范给出的参考值均偏小，只有当滴头间距为0.2 m时，规范给出的参考值偏安全.

3) 随着压力的增加，使毛管的过水断面发生变化，当量直径也随之增大，最终导致毛管的均匀度增大.而当毛管壁厚小于0.30 mm时，壁厚对毛管均匀度影响较小；当毛管壁厚超过0.30 mm时，均匀度受毛管壁厚影响较显著.最后给出了不同压力和壁厚下毛管极限铺设长度，发现壁厚对毛管极限铺设长度影响较小，这可能是由于算例中滴头额定流量较小导致.