基于组合赋权-改进可拓云的装甲车辆PHM系统性能评估

秦 涛，鲁冬林，曾拥华

(1.陆军工程大学 研究生院，南京 210001；2.中国人民解放军32228部队，南京 210012)

0 引言

随着武器装备技术的快速发展，装甲车辆分系统的技术集成度和复杂度越来越高，其维修保障问题也摆在了更加突出的位置[1]。预测与健康管理(PHM, prognostics and health management) 技术的出现把实现装备在线维修保障变成了可能，将传统的视情维修从基于故障问题转变为基于性能状态[2]，有效提高了装甲车辆关键部件的安全性、可靠性、维修性和保障性,进而提升了使用单位的装备战备完好率和任务成功率。而PHM系统目前种类较多，其性能的好坏将很大影响到在线维修保障的效能，因此如何有效对PHM系统进行评估成为了目前研究的热点。翟梅杰等学者结合装甲车辆特点，根据装备组成构建了一套装甲车辆PHM系统性能度量指标体系[3-5]；吴守军等学者综合AHP法与模糊综合评判法实现了装甲车辆PHM系统应用范围的确定[4]；王冠球等学者在确定指标权重的基础上。利用模糊综合评价法对8套装甲车辆的PHM系统进行综合评价[6]；评估方法的选择并无好坏之分，关键需贴合装甲车辆PHM系统性能的特点，能够实现客观准确的评价；本文在王冠球高级工程师研究的基础上[6]，对其赋权方法进行了客观修正，同时在模糊综合评判时，引入改进可拓云理论构造因素模糊评判矩阵，有效处理不同评语等级之间界限分明或过于模糊的问题，在评估结果呈现上实现了定量和定性综合评价。

1 装甲车辆PHM系统简介

1.1 系统构成

装甲车辆装备PHM系统是实现装甲装备各分系统故障预测与健康管理的新兴手段，能够通过数据采集、数据传输和数据分析等手段完成装备在线性能监测与评估。图1是装甲车辆PHM系统构成示意图，主要包含了车载测控设备、通信设备和地面服务器三大模块。具体组成及功能如下：

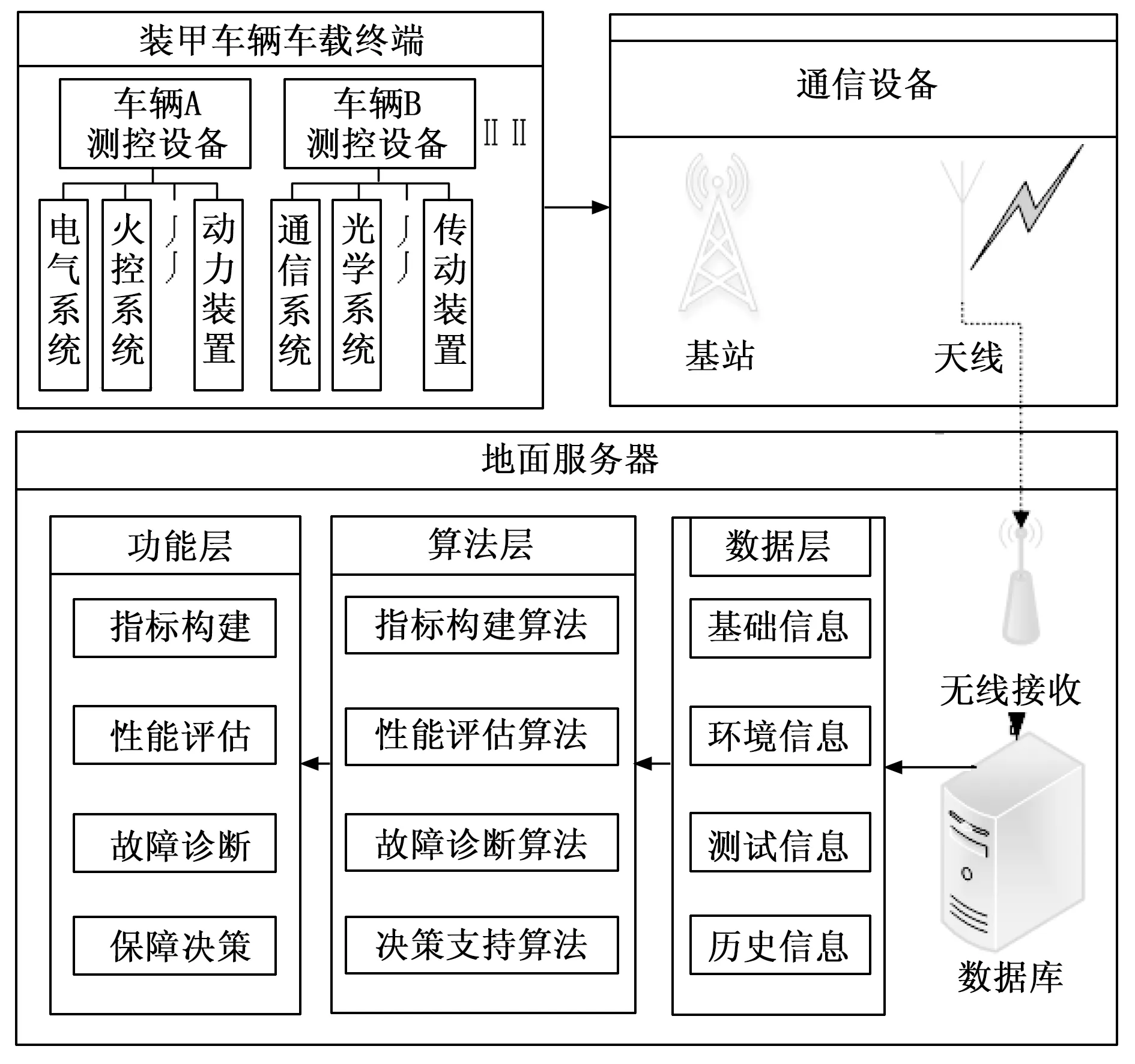
图1 装甲车辆PHM系统构成示意图

1)车载测控设备。该模块装配在装甲车辆需要检测的各个系统(电气、火控、底盘等)，主要完成装备技术状态信息和位置信息的采集，实现监测和采集功能；

2)通信设备。该模块主要实现数据信息传输功能，将采集到的装甲车辆技术状态信息和位置信息传输到地面服务器；

3)地面服务器。该模块主要由数据库、PHM系统和相应算法组成，在对历史样本数据分析的基础上，结合相应算法实现对装甲装备进行故障诊断和预测，并辅助业务部门开展维修保障决策。

1.2 评估指标体系

构建科学合理的装甲车辆PHM系统性能评估指标体系，是开展性能度量评估的基础环节，也可为PHM系统性能优化、设计改良提供参考。在对不同领域指标体系构建方法的研究基础上，本文参考了翟梅杰在《装甲车辆PHM系统性能度量指标体系构建》文中的指标体系，见表1，并在此基础上开展评估。通过观察，该指标体系提出了总体性能度量指标、车载终端度量指标、通信设备度量指标和地面服务器度量指标共26个性能评估指标，包含了9个定性指标和17个定量指标。

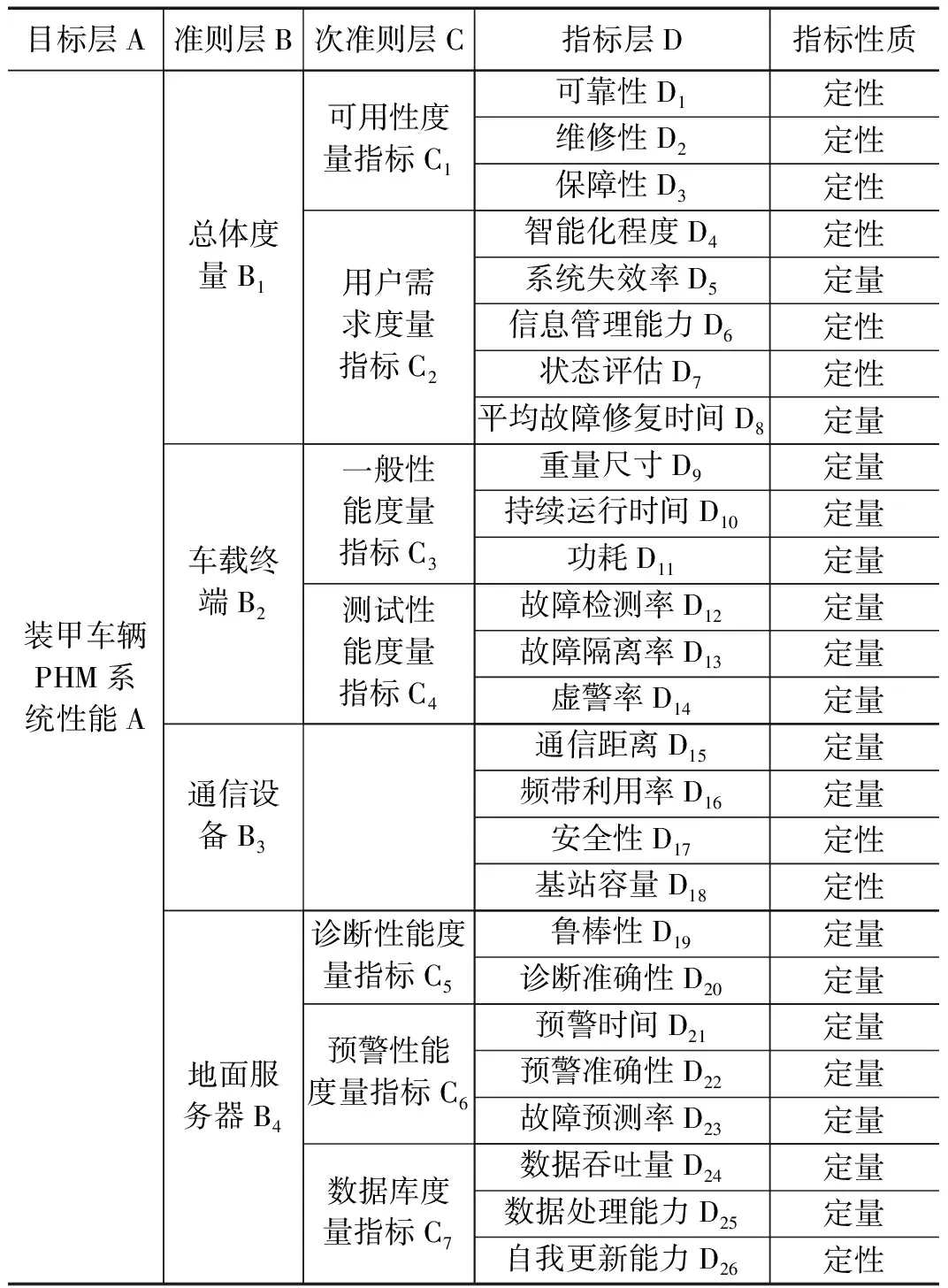
表1 装甲车辆PHM系统性能度量评估指标体系

1.3 改进评估思路

本文在学者王冠球开展装甲车辆PHM系统性能评估的基础上，对评估方法和模型进行了改进优化，具体思路如下：在原文利用层次分析法确定权重的基础上，增加客观赋权方法，按照“AHP-熵权”组合赋权方法实现主客观赋权相统一；其次，改进模糊评判矩阵构造方法，引入基于最优云熵的改进可拓云理论实现指标评估值相对评语等级关联度值的确定，保证了评语等级界限适当的模糊性；最后通过模糊综合评判实现装甲车辆PHM系统性能的定性和定量评估，具体思路见图2。

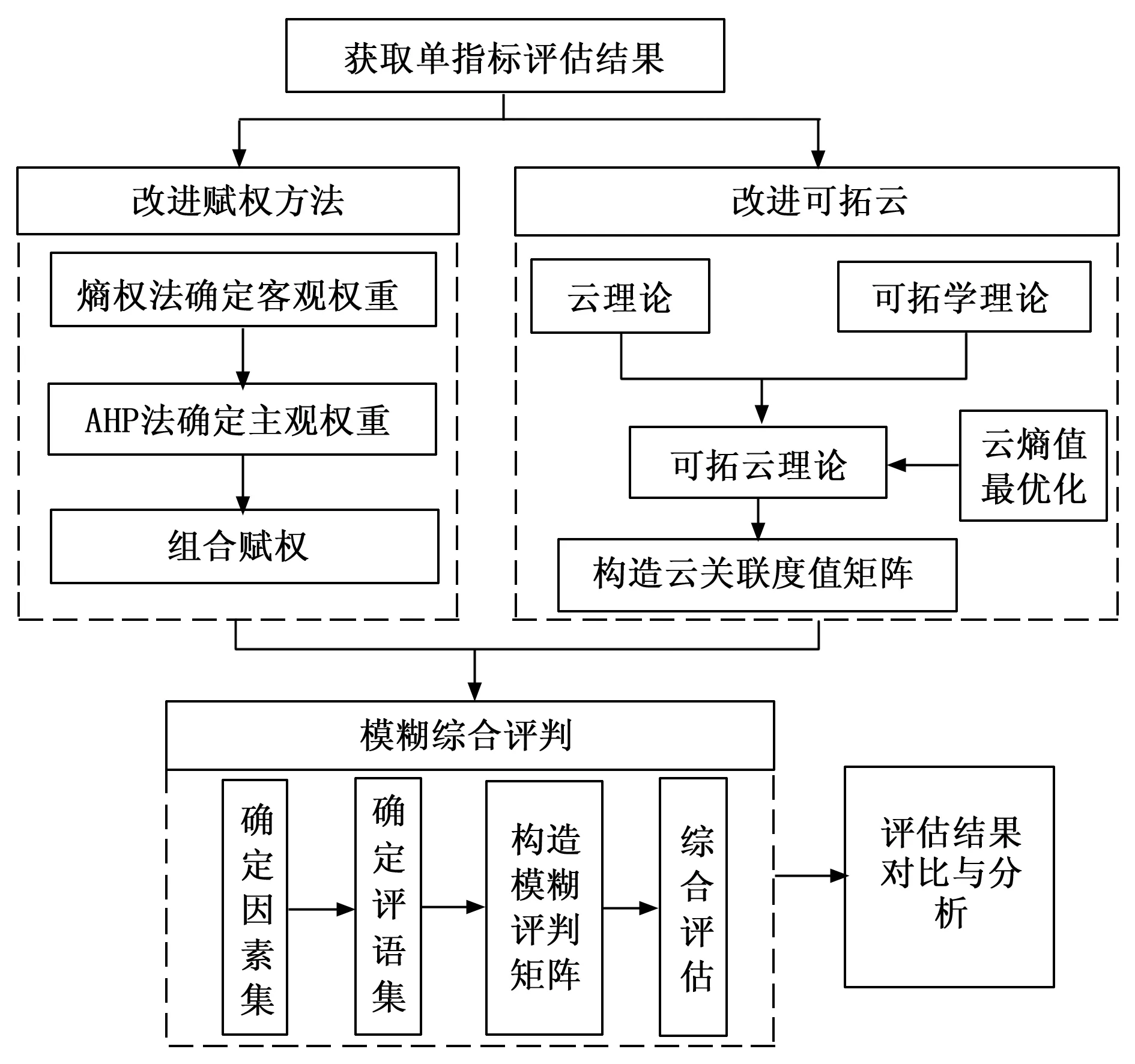
图2 改进评估思路框架图

2 评估模型

2.1 组合赋权法评估模型

为了确保装甲车辆PHM系统性能评估结果客观准确，本文采用层次分析法与熵权法相结合的组合赋权法进行权重确定。

2.1.1 基于AHP的评估指标主观赋权

层次分析法是运筹学理论中比较成熟的方法，主要是在多层次指标框架模型中，通过把隶属于同一上级的同一层次指标进行两两比较判断，形成低层次相对于高层次的相对重要性权重系数，再通过和上层次指标的相对重要性权重系数进行加权综合计算，得到各层指标相对于总目标层的重要性权重系数。其步骤如下：

1)构建层次化结构模型：结合评估指标体系构建指标横向之间的比较关系、纵向之间的逻辑归属关系以及重要级别，建立自上而下的层次化结构模型。

2)明确比较判断标度：采用“1～9”九标度法来描述两者重要性比较结果，其标度及其标准见表。

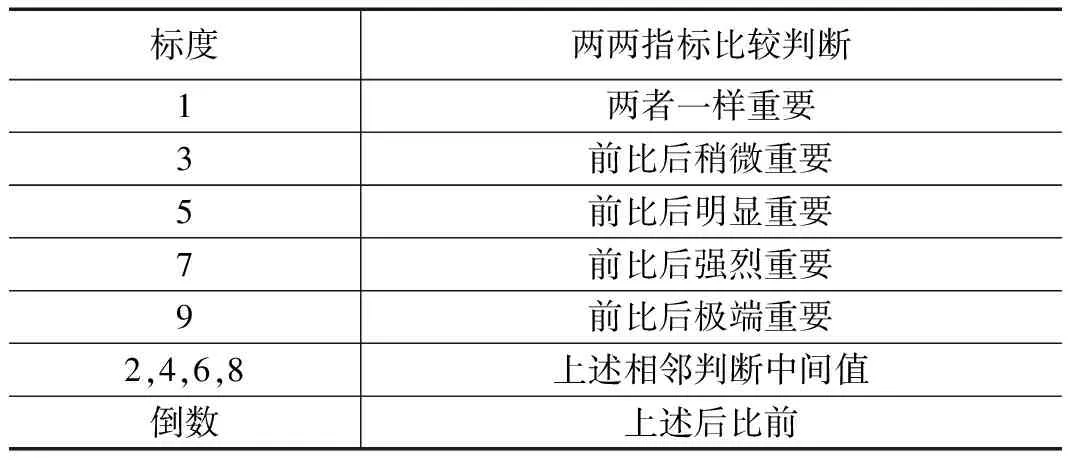
表2 “1～9”九标度属性

3)构造比较判断矩阵：通过征询专家组意见，得到不同专家构造出的不同判断矩阵，并对数据进行综合处理，得到一个综合判断矩阵。假设专家组人数为n，指标体系某层有m个因素参与比较，则第k位专家构造出的判断矩阵为：

Ak=(aijk)m×m,i,j=1,2,3,...m;k=1,2,3,...,n

(1)

aijk表示第k位专家将指标i和指标j比较所得的标度值。综合n位专家的判断矩阵，得到综合判断矩阵为：

(2)

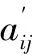
(3)

当CI<0,1时，可认定判断矩阵符合一致性要求，否则需进行调整。

5)确定合成权重：在确定各层次指标相对权重并经过一致性检验后，则可以根据各级指标的权重求得各层指标相对于总目标的合成权重。假设由AHP法得到的主观赋权向量为W1=(ω11,ω21,...ωi1,...ωn1),n为指标数量。

2.1.2 基于熵值法的评估指标客观赋权

熵值法是根据评估指标信息量的大小确定指标权重系数的方法，借鉴热力学“熵”的概念，熵值越小则该指标无序度越小，在评估中起到的作用越大，用以度量指标信息量的大小。其具体步骤如下：

1)获取数据，构建原始数据矩阵(Zij)m×m，其中m为评估对象数量，n为指标数量；

2)计算第j个指标下第i个评估对象的特征比重Pij：

(4)

3)计算第j个指标熵值ej：

(5)

4)计算差异系数gj：

gj=1-ej

(6)

对于给定的j，zij差异越小，ej越大，反映指标对评估对象的作用越小。

5)确定权重系数ωj。

(7)

假设由熵值法得到的客观赋权向量为W2=〔ω12，ω22，…ωi2，…ωn2〕,n为指标数量。

2.1.3 组合赋权

在确定主客观权重系数向量W1、W2的基础上，将主客观权重按照一定的系数组合，得到将集成后的权重向量W：

(8)

式(8)中的α1取值视情确定，若α1∈[0,0.5],则赋权偏向客观指标数据，若α1∈[0,0.5],则赋权偏向专家经验。常用的α1确定方法有专家咨询法、离差和最小计算法等。本文采取专家咨询法确定α1值。

2.2 基于最优云熵的改进可拓云评估模型

2.2.1 云理论数字特征简介

假定定量论域U可以用精确数值来表示范围，C是该定量论域U上的定性概念。如果满足：1)定量值x∈U，且x是C的一个随机实现；2)x对于定性概念C的隶属度μc(x)∈[0,1]是具有稳定倾向的随机数，那么就把x在定量论域U上的分布称之为云模型，云滴可表示为〔xi,μi(xi)〕,i=1,2,3,…,n。

云的数字特征用期望Ex、熵、En、超熵He三个数值来表示，如图3所示。其中，期望Ex表示定性概念C的中心值；En熵是定性概念C的不确定性度量，En越大，表示亦彼亦此性越明显，确定性的定量描述就越难；超熵He是熵之熵，反映了熵En的不确定性度量，He越大，云滴隶属度的随机性就越大，云层就越厚。

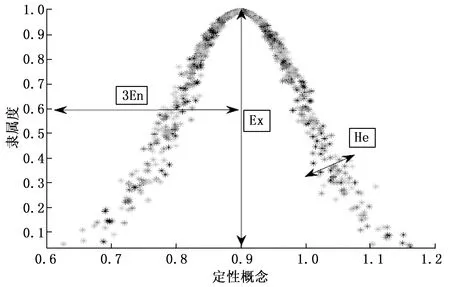
图3 云模型的数字特征

2.2.2 可拓云理论

本文以正态云为例，假定某个评语等级的上下界限为[Vmin,Vmax],可求得该评语等级所对应的云模型数字特征如下：

(9)

其中：λ体现评语自身的模糊程度,根据经验设定，本文取0.01。

物元R=〔N,C,v〕是可拓学理论的基础模型，旨在通过建立关联函数描述事物特征，其中N表示物，C表示物的特征，v表示特征值。在构建可拓云模型的过程中，将上述云模型的数字特征替换物元R中的特征值，即得到式(10)中的可拓云模型，可以有效结合可拓学和云理论的优点，提升处理不确定性的能力。

(10)

2.2.3 可拓云理论改进方法

2.2.3.1 一般云熵计算

在传统可拓云模型中，对于某个评语等级，在上下界限[VminVmax]范围内，云期望Ex的计算公式为Ex=(Vmax+Vmin)/2，云超熵He一般是常数，根据经验设定。云熵En作为反映属性概念不确定性的关键影响因素，其取值大小对于评估结果判定有着重要影响。通过有关文献的查阅，可将一般的云熵计算方法大致总结为两种，具体如下：

1)“3En”规则:

此法忽略了(-∞,En-3En)和(Ex+3En,+∞)区域的云滴，将[Ex-3En，Ex+3En]之内的云模型视为完整模型，是传统云理论常用的云熵计算方法，其特征是相邻云之间的边界分明、评语等级划分清晰，计算公式为：

(11)

2)“50%关联度”规则：

“50%”是指将评语等级的临界值和相邻等级的关联度视为相同且均为50%，相较于“3En”规则，“50%关联度”规则下的边界更具模糊性，计算公式为：

(12)

2.2.3.2 最优云熵计算

以上两种云熵计算方法分别突出了评语等级的分明性和模糊性，但不同的方法计算出的云熵值很可能导致评估结果出现冲突。为了兼顾两种计算方法优点，本文采用了一种改进云熵计算方法：

假定某评估指标分数值为xi,对应k个评语等级，可生产k个评语等级云模型，其中等级云的期望值、云熵值和超熵值矩阵分别为：

将云数字特征(Ex，En，He)通过正向云发生器生成云滴图，根据云图内外包络线确定云滴图的内外关联度曲线l1,l2，云滴中间位置为期望关联度曲线L，以数字特征(30,6,0.4)为例，生成云滴图和相应关联度曲线如图4所示。

图4 云滴和关联度曲线图

关联度内外曲线的表达式为：

(13)

表3 评语等级云模型数字特征

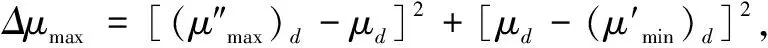
d=1,2,…,k

(14)

以实现评估指标值xi相对于k个评语等级可拓云模型的最大关联度偏差之和最小化为优化目标，可构造目标函数如式(15)，并最终求得基于最优云熵算法的云熵值矩阵En1×k=[En1,En2,…，Enk]：

(15)

在得到最优云熵值矩阵En1×k=[En1,En2,…，Enk]的基础上，可以由式(16)计算评估指标分数值xi与不同评语等级之间的关联度μd：

μd=e(x-Exd)2/2(End)2,d=1,2,…,k

(16)

2.3 模糊综合评判

2.3.1 确定因素集和评语集

根据表1中的层次化结构，可构建两层因素集：其中第一层总目标因素集为U={B1,B2,B3,B4}，第二层子目标因素集有4个，分别为U1={C1、C2}、U2={C3、C4}、U3={B3}、U4={C5、C6、C7}。本文结合装甲车辆PHM系统实际情况，将性能度量评语等级分为：优(v1)、良(v2)、中(v3)、一般(v4)、差(v5),即构建评语集V={v1、v2、v3、v4、v5}

2.3.2 构造综合评判矩阵

1)确定指标取值范围:结合装甲车辆PHM系统的实际情况，在咨询专家的基础上，为5级评语分别设置取值范围，具体见表4。

表4 评语等级取值范围

2)确定指标对等级的隶属度:在确定指标对等级隶属度时，相邻评语等级之间通常不是界限分明的，需要考虑模糊处理。本文采用云模型进行确定定量指标的隶属度，具体做法是按照公式(17)计算5个评语等级的云模型数字特征，并分别生成如图5所示的云滴图，然后按照公式(18)计算各指标值相对于不同评语等级d的关联度值。

图5 指标值对评语等级关联关系云滴图

(17)

(18)

其中:Vmax和Vmin表示评语等级取值范围区间的上下限，λ体现评语自身的模糊程度,根据经验设定；μd表示指标值相对于评语等级d的关联度值，当指标值小于30或大于95时，其隶属于差或优的关联度值为1。

3 实证分析

3.1 数据获取

获取指标数据是开展评估的基础，根据论文[6]中获取的指标评价值，按照5级评语等级划分，列举4套装甲车辆的指标分数，见表5。

3.2 组合权重计算

基于AHP法的权重计算，主要参考论文[6]现有成果，具体见表6；基于熵权法的权重计算，结合表5中4个评估对象、7个评估指标的数据，按照公式(4)～(7)通过Matlab计算得到，具体见表7。

表5 四套装甲车辆PHM系统性能评估指标分数

表6 AHP法确定主观权重系数一览表

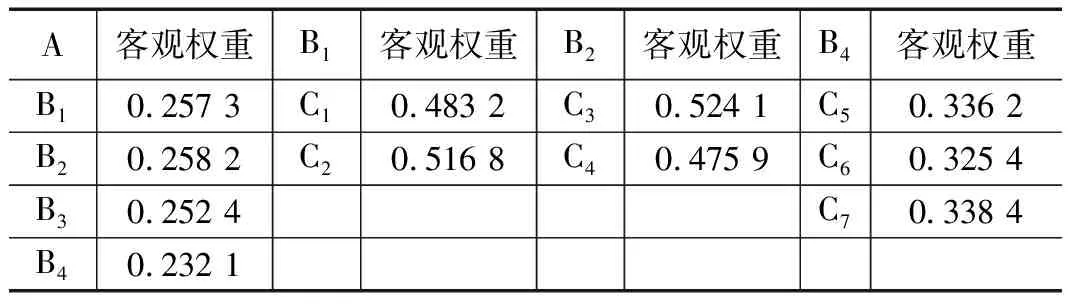
表7 熵值法法确定主观权重系数一览表

在获取评价指标主客观权重系数后，按照公式(8)计算组合权重。通过邀请多位专家对μ值进行打分，并将结果取平均值，得到最终μ值为0.60，表示以专家经验为主，以指标客观数据为辅。得到的指标组合权重见表8。

表8 组合权重系数一览表

3.3 综合评估

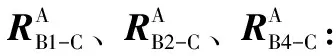
通过计算得到如下结果：

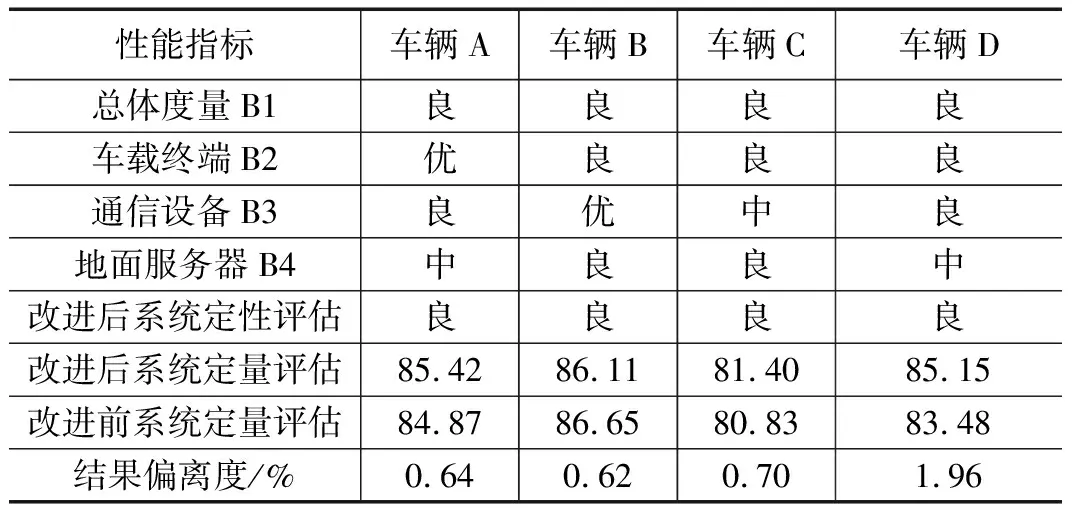
表9 四套车辆PHM系统综合评价结果一览表

计算结果表明，运用本文模型计算出的PHM系统性能定量评价结果与改进前的结果偏离度整体控制在2%以内，如图6所示，验证了本文改进评估模型的有效性和实用性；同时，在两者趋于一致的同时，经过熵权法的修正，评估结果兼具主客观性，其中车辆D的PHM系统定量评价结果相较原文更接近良好水平，增加了评估结果的可信度和准确性。此外，相较论文[6]，本文同时对具体指标给出了定性和定量2种评价结果，数据呈现更加直观明朗。

图6 改进前后定量评估结果比对图

4 结束语

本文在对装甲车辆PHM系统介绍的基础上，明确了相较于论文改进评估的思路，首先采用“AHP-熵权”组合赋权法计算指标权重系数；其次在构建因素集模糊评判矩阵过程中，对传统云理论进行改进，按照最优云熵算法计算指标分数相对于评语等级的关联度值，进而构建综合评判矩阵，较好的处理了不同评语等级之间界限分明或过于模糊的问题；最后按照模糊综合评判模型，对4套装甲车辆PHM系统进行了综合评估，得到了定量和定性2种评估结果。结果表明，改进后的模型在不失有效性的同时，能够得到更加客观准确的评估结果。